Similar presentations:
Наглядные изображения
1. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Направления обучения«Архитектура»
«Реконструкция и реставрация архитектурного наследия»
«Дизайн архитектурной среды»
«Градостроительство»
2. Лекция 6
Солодухин Е.А., 20173. Наглядные изображения
34.
45.
56.
67. Аксонометрические проекции
8.
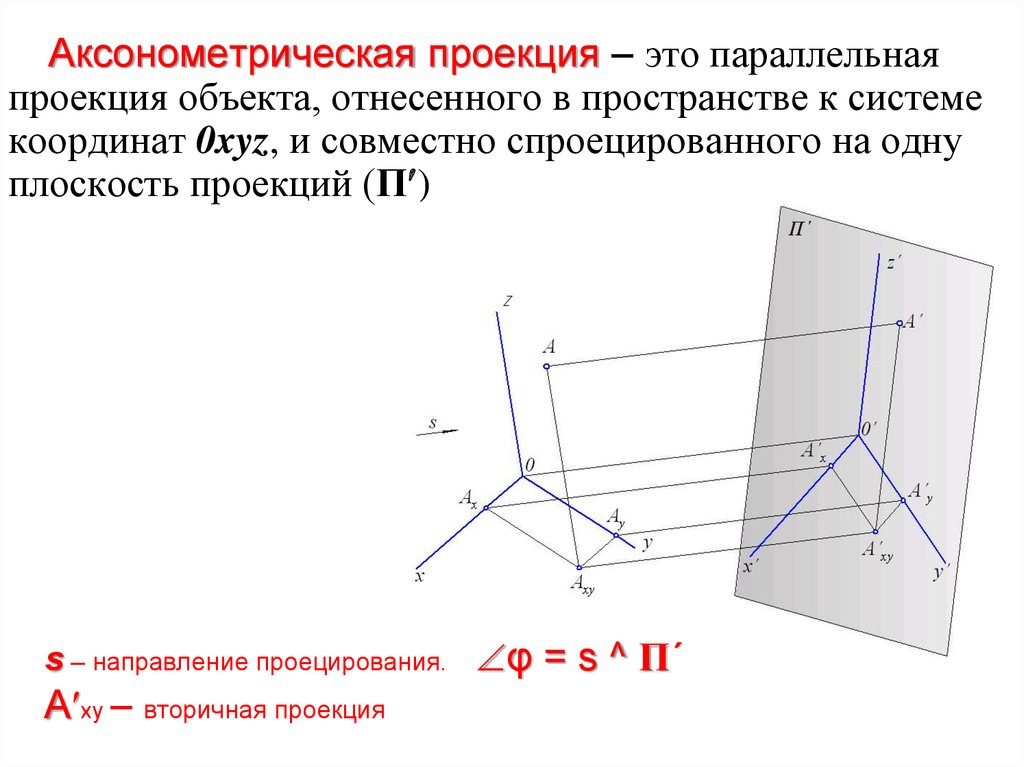
Аксонометрическая проекция – это параллельнаяпроекция объекта, отнесенного в пространстве к системе
координат 0xyz, и совместно спроецированного на одну
плоскость проекций (П )
s – направление проецирования. φ = s ^ П´
А xy – вторичная проекция
9. Виды аксонометрических проекций в зависимости от направления проецирования
Прямоугольные (s П φ = 90º)Косоугольные (s П φ ≠ 90º)
10. Расположение пространственной системы координат 0xyz относительно плоскости проекций
• В прямоугольной аксонометрии ни одна изкоординатных плоскостей системы 0xyz не
может быть расположена параллельно
плоскости проекций П´.
• В косоугольной аксонометрии одна из
координатных плоскостей системы 0xyz может
быть расположена параллельно плоскости
проекций П´.
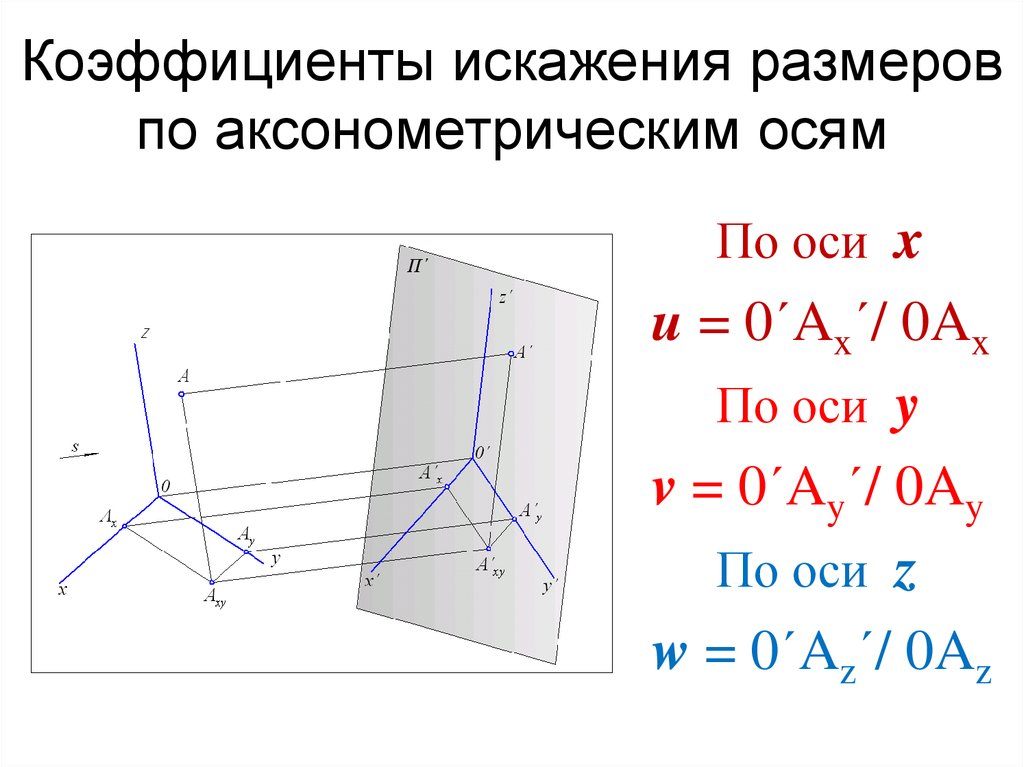
11. Коэффициенты искажения размеров по аксонометрическим осям
По оси xu = 0´Ax´/ 0Ax
По оси y
v = 0´Ay´/ 0Ay
По оси z
w = 0´Az´/ 0Az
12. Виды аксонометрических проекций в зависимости от соотношения величин коэффициентов искажения по аксонометрическим осям
• u = v = w - изометрия• u=v≠w
u ≠ v = w - диметрия
u≠w=v
• u ≠ v ≠ w ≠ u - триметрия
13. Стандартные аксонометрические проекции ЕСКД ГОСТ 2.317-69
Стандартныеаксонометрические
проекции
ЕСКД ГОСТ 2.317-69
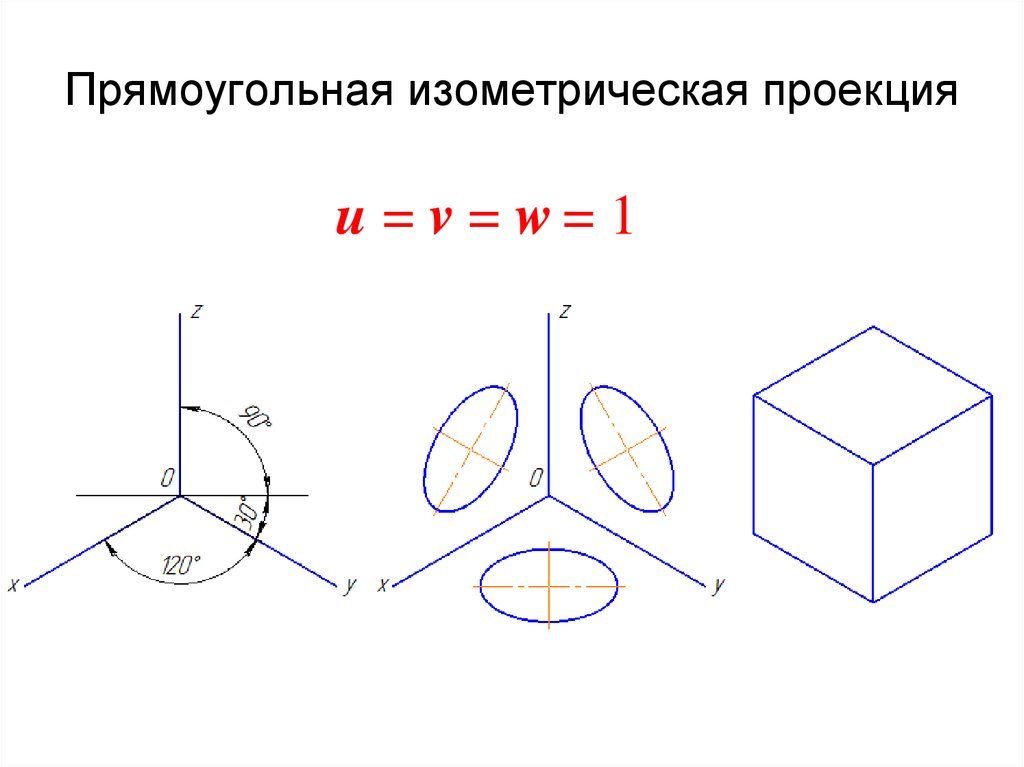
14. Прямоугольная изометрическая проекция
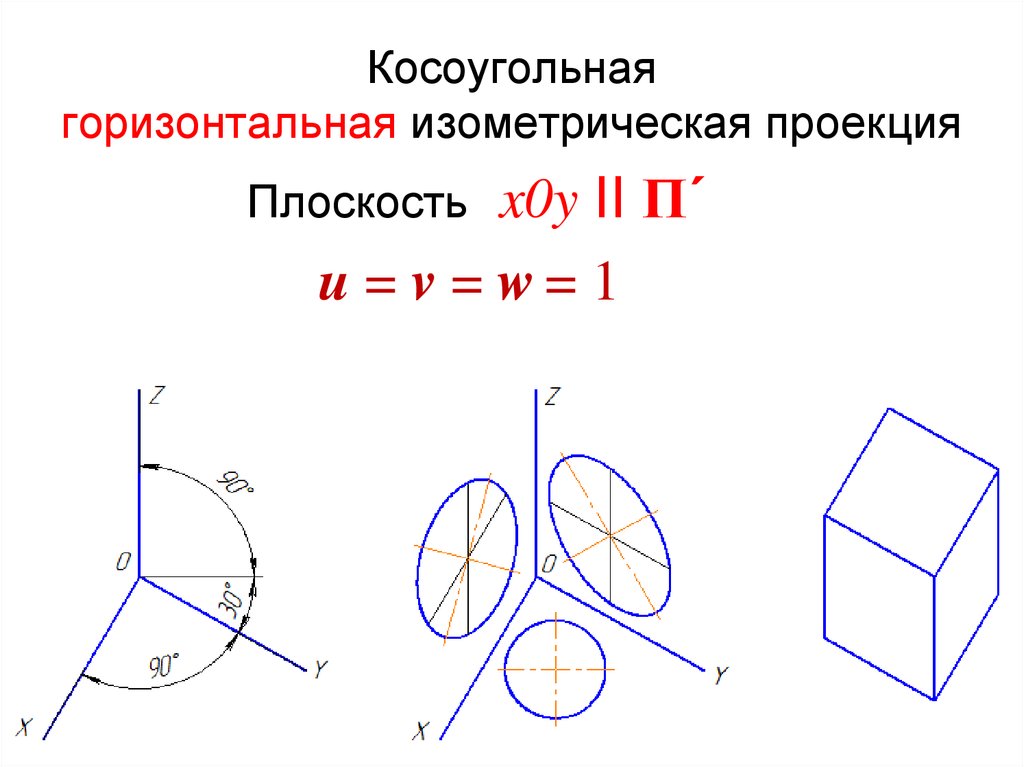
u = v = w= 115. Косоугольная горизонтальная изометрическая проекция
x0y II П´u = v = w= 1
Плоскость
16. Линейная перспектива
1617.
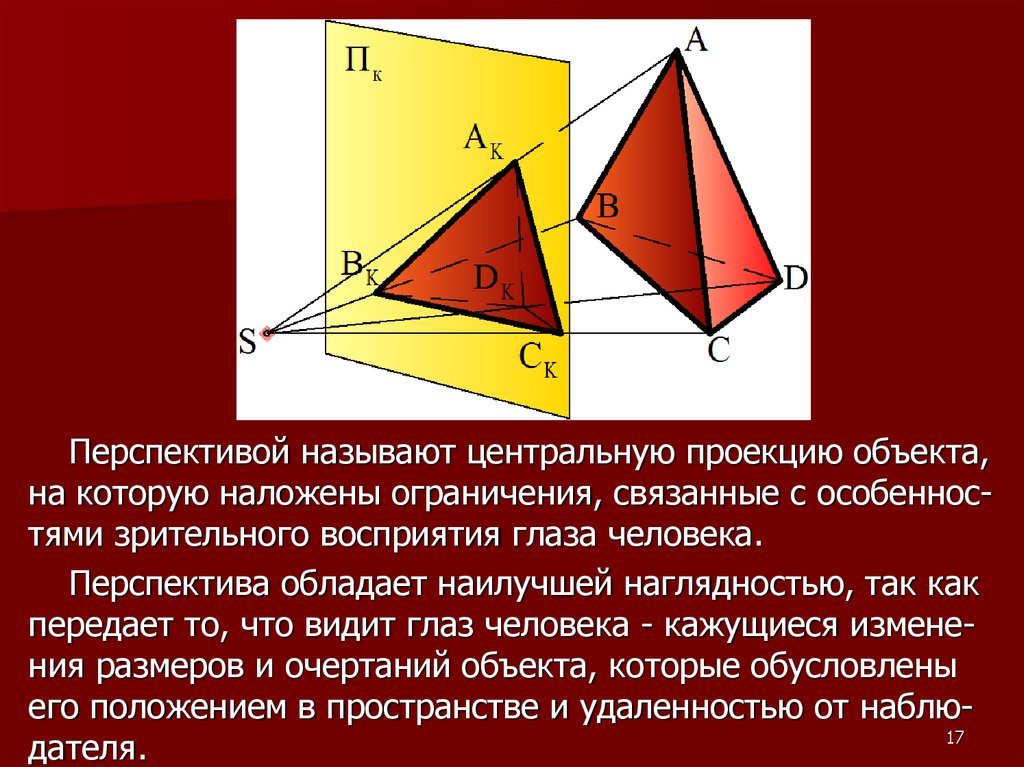
Перспективой называют центральную проекцию объекта,на которую наложены ограничения, связанные с особенностями зрительного восприятия глаза человека.
Перспектива обладает наилучшей наглядностью, так как
передает то, что видит глаз человека - кажущиеся изменения размеров и очертаний объекта, которые обусловлены
его положением в пространстве и удаленностью от наблю17
дателя.
18. Виды перспективы
На плоскости – линейная перспектива.Если плоскость расположена
горизонтально, то перспектива плафонная
(для росписи потолков).
На цилиндрической поверхности –
панорамная перспектива.
На сферической поверхности – купольная
перспектива.
18
19. Общий принцип построения перспективы точки
SA ∩ Пк = АкАк – перспектива точки А
SA1 ∩ Пк = А1к А1к – вторичная проекция точки А
АкА1к О1О2
19
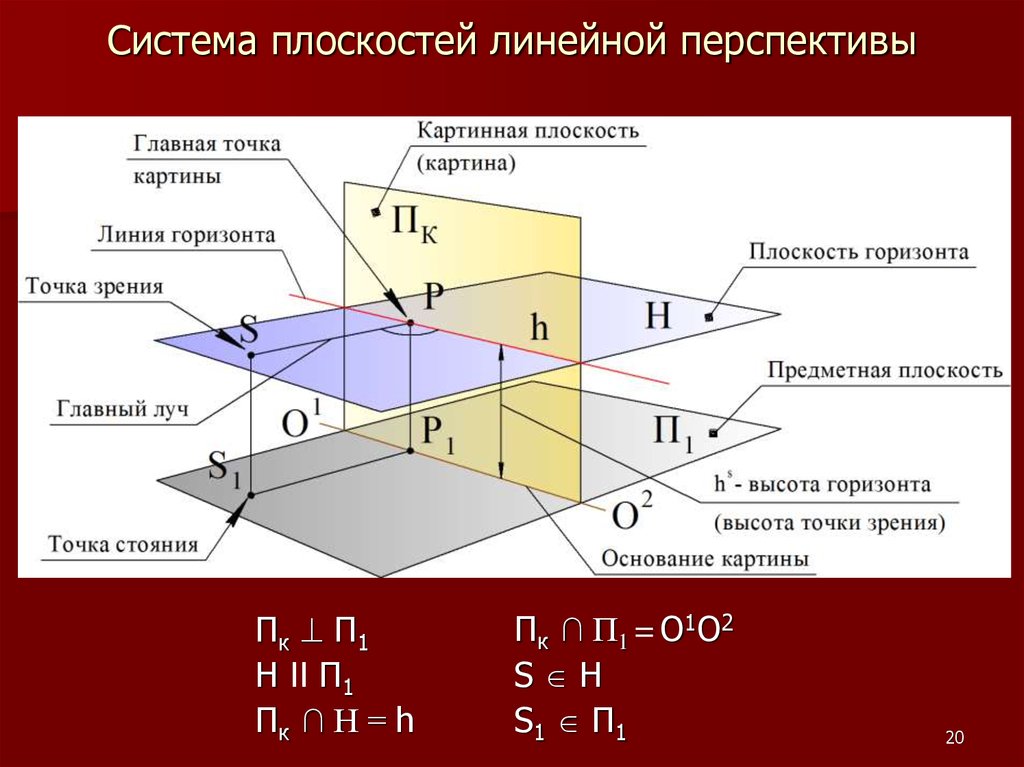
20. Система плоскостей линейной перспективы
Пк П 1H II П1
Пк ∩ Н = h
Пк ∩ П1 = О1О2
S H
S1 П1
20
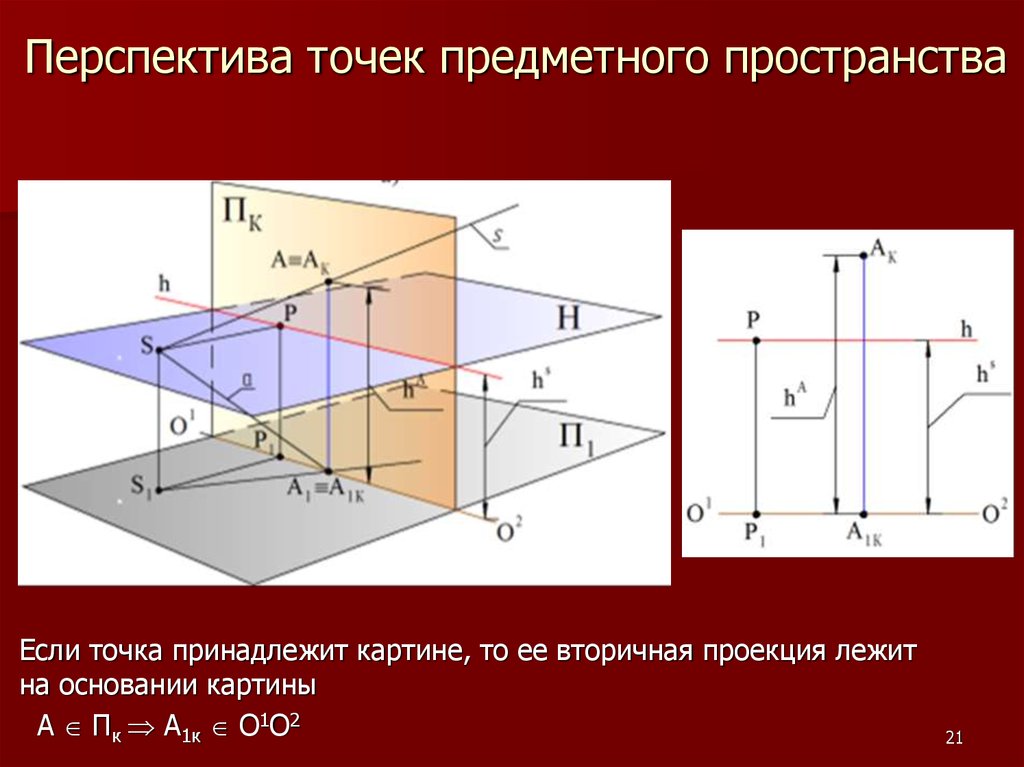
21. Перспектива точек предметного пространства
Если точка принадлежит картине, то ее вторичная проекция лежитна основании картины
А Пк А1к О1О2
21
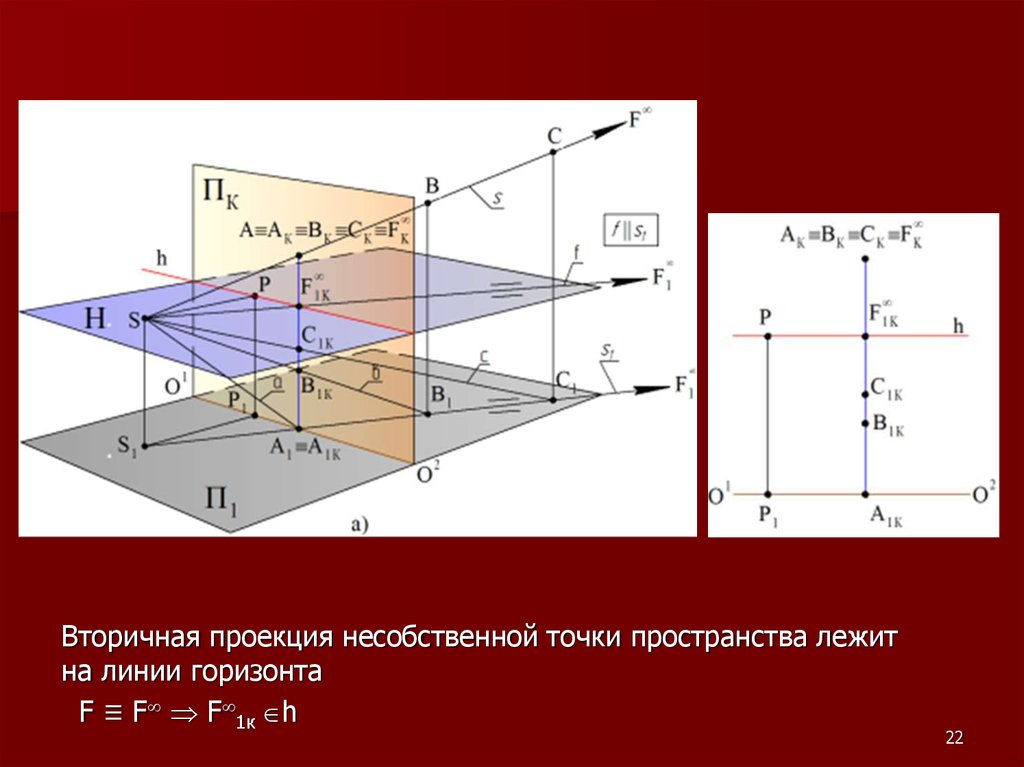
22.
Вторичная проекция несобственной точки пространства лежитна линии горизонта
F ≡ F F 1к h
22
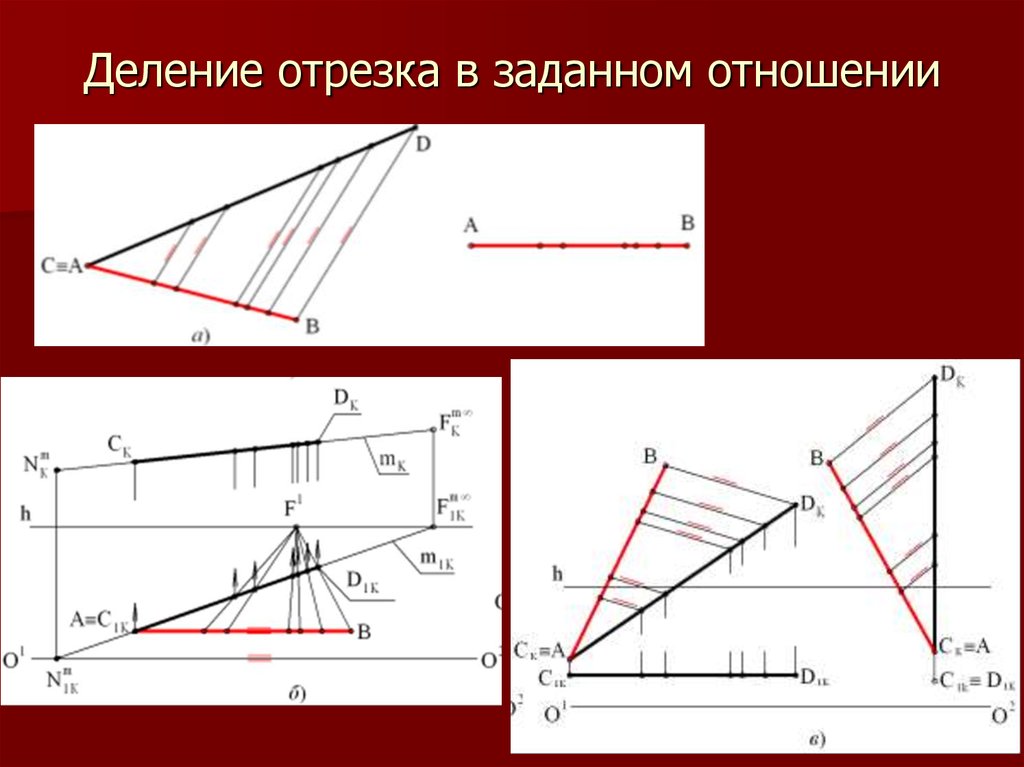
23. Перспектива прямой
2324.
В перспективе прямая(например, m) задается двумя
точками – m (N, F∞).
Точка N – начало прямой.
Принимается точка
пересечения прямой с
картинной плоскостью.
N = m ∩ Пк
Точка F∞ - несобственная
точка.
N Пк Nк ≡ N N1к O1O2;
F∞ F1к h.
25.
26.
F2ks2
S2
N2k
m2
х12
s1
P1
m1
F1k
S1
N1k
Пк1
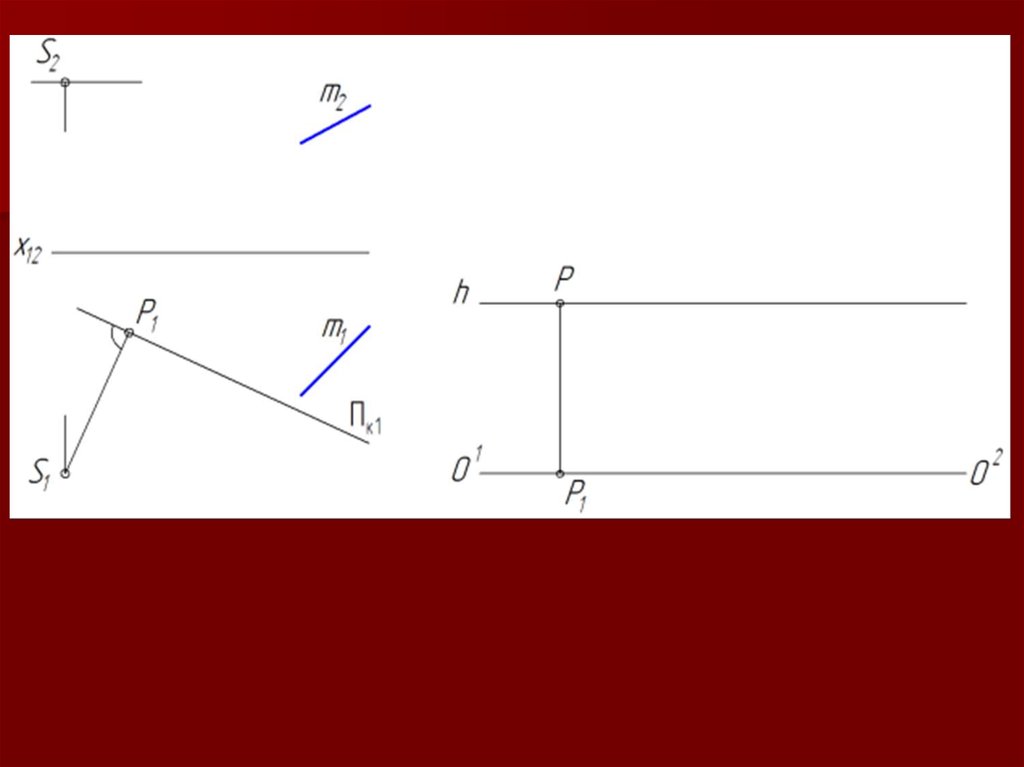
Чтобы получить (увидеть)
несобственную точку F∞,
принадлежащую прямой m,
находясь в точке зрения S,
необходимо направить луч зрения
параллельно прямой m.
Точка F∞k пересечения луча s с
картинной плоскостью Пk и будет
изображением несобственной точки
F∞.
S s, s II m и s ∩ Пk = F∞k
Чтобы получить точку N начала
прямой m, необходимо продолжить
прямую до пересечения с
картинной плоскостью
m ∩ Пк= N
26
27.
F2ks2
S2
m2
Fk
c
P F1k
d
а
а
m1k
d
s1
P1
m1
O
F1k
b
h
Nk
c
х12
mk
N1k
1
P1
b
O
Пк1
S1
27
2
28.
По положению точки F k относительно линии горизонтаможно судить о положении прямой
m относительно
∞
предметной плоскости.
Если F k выше линии горизонта, то прямая восходящая.
Если F k ниже линии горизонта, то прямая нисходящая.
Если F k лежит на линии горизонта, т.е. F k ≡ F 1k , то прямая
является горизонталью.
FK
h
O
восходящая
mK
нисходящая
h F 1K
Р
F 1K
1
NК
m 1K
FK
2
Р1
а)
N 1К
mK
m 1K
Р1
б)
Р
N 1К
N 1К
д)
Р
h
O
2
O
1
h
Р
m 1K
1
е)
перпендикулярна
картине
F K F 1K Р
h
NК
m 1K
2
O O1
Р1
N 1К
в)
горизонтальнопроецирующая
параллельна
картине
mK
F 1K
m 1K
Р1
m 1K
O O1
?
O
NК
mK
Р
2
O O1
m K F N
K
K
1
F K F 1K
Р
проецирующая
h
горизонталь
2
O
Р1 O Р1 Р1
mK
h
NК
O
г)
mK
m 1K
2
NO
1К
ж)
28
2




















 drafting
drafting