Similar presentations:
Начертательная геометрия. Линейная перспектива. (Лекция 6-7)
1. Линейная перспектива
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯЛекция 6
Линейная перспектива
Направление
обучения –
«Архитектура»
1
2.
23.
34.
45.
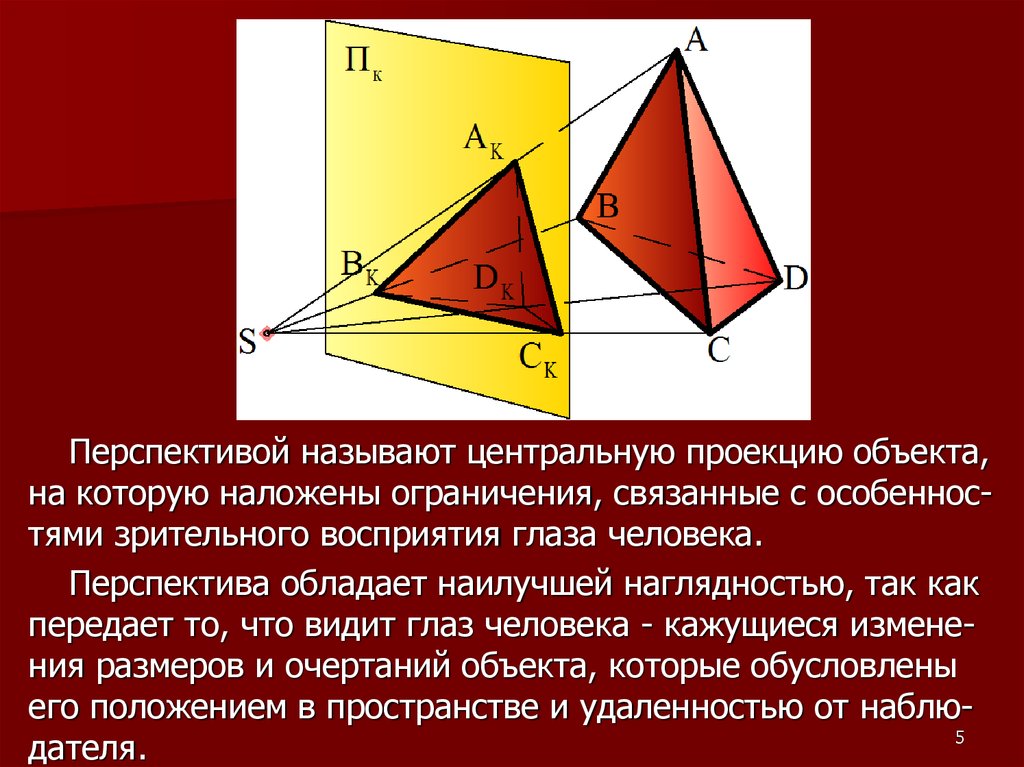
Перспективой называют центральную проекцию объекта,на которую наложены ограничения, связанные с особенностями зрительного восприятия глаза человека.
Перспектива обладает наилучшей наглядностью, так как
передает то, что видит глаз человека - кажущиеся изменения размеров и очертаний объекта, которые обусловлены
его положением в пространстве и удаленностью от наблю5
дателя.
6. Виды перспективы
На плоскости – линейная перспектива.Если плоскость расположена
горизонтально, то перспектива плафонная
(для росписи потолков).
На цилиндрической поверхности –
панорамная перспектива.
На сферической поверхности – купольная
перспектива.
6
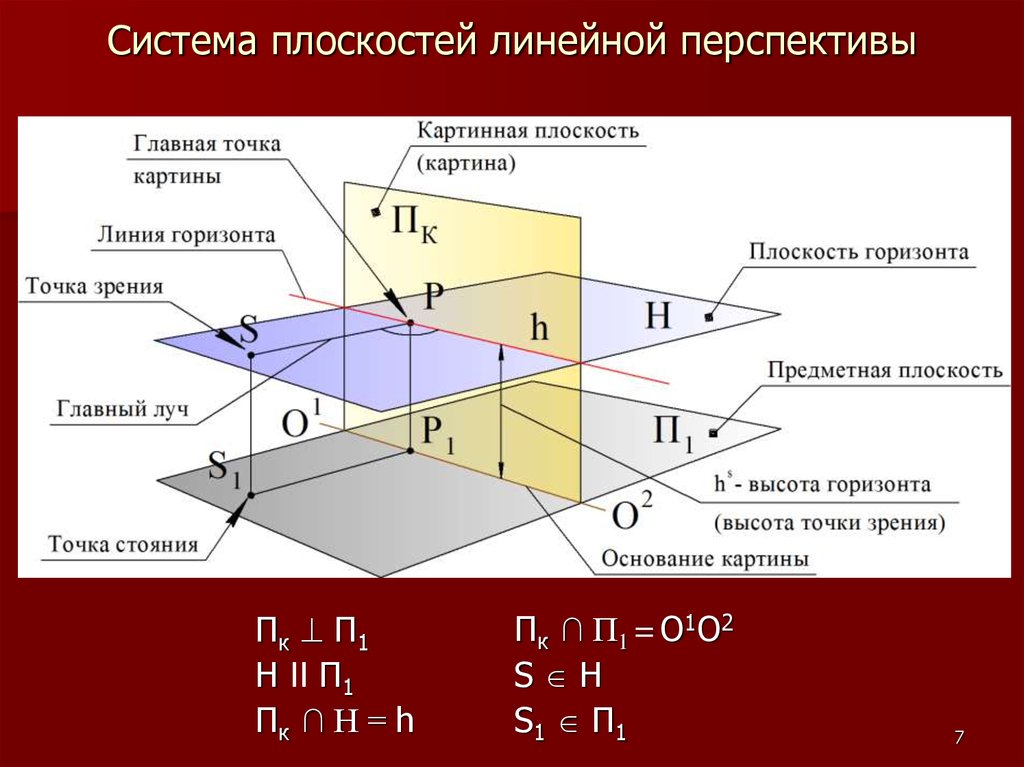
7. Система плоскостей линейной перспективы
Пк П 1H II П1
Пк ∩ Н = h
Пк ∩ П1 = О1О2
S H
S1 П1
7
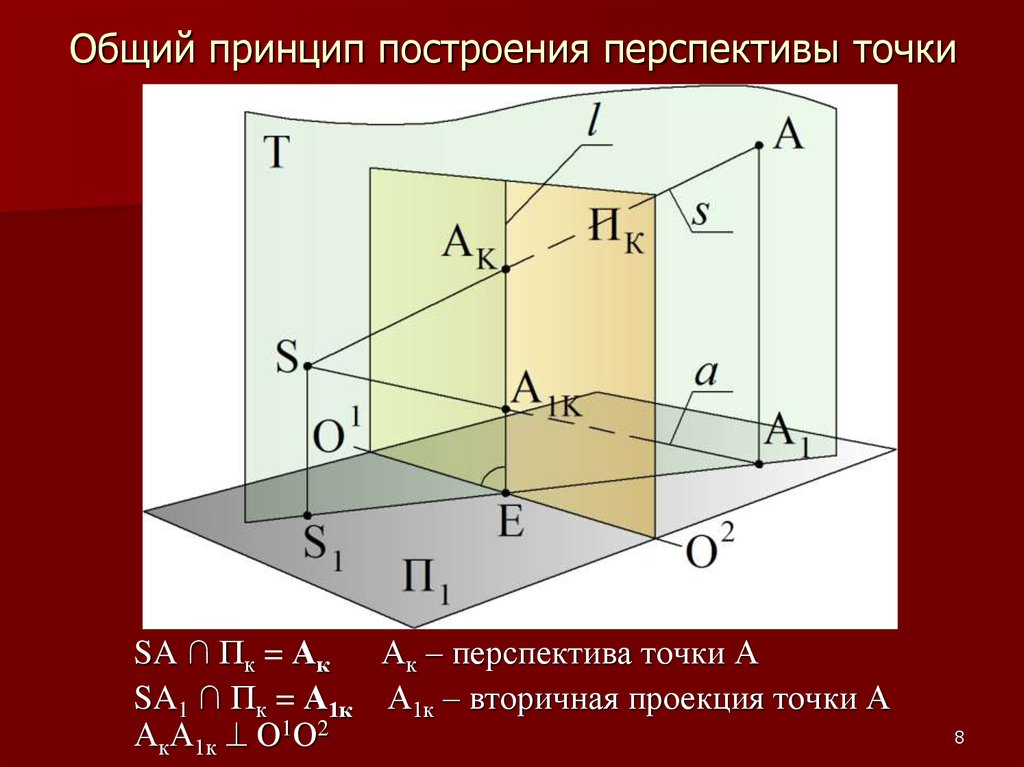
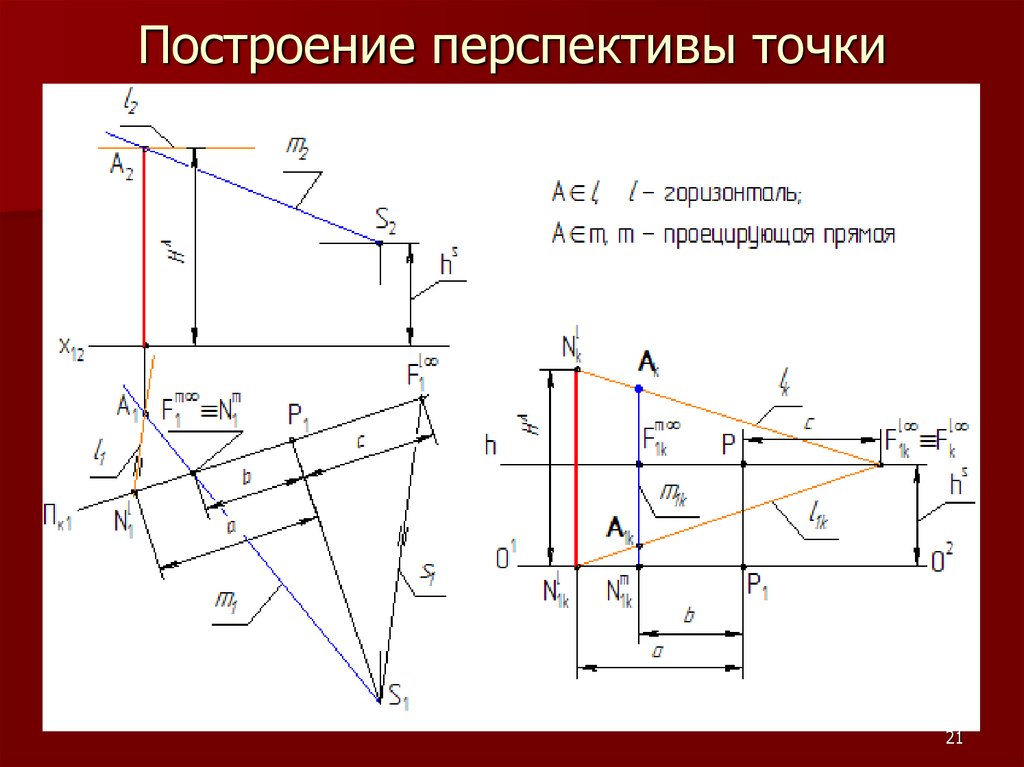
8. Общий принцип построения перспективы точки
SA ∩ Пк = АкАк – перспектива точки А
SA1 ∩ Пк = А1к А1к – вторичная проекция точки А
АкА1к О1О2
8
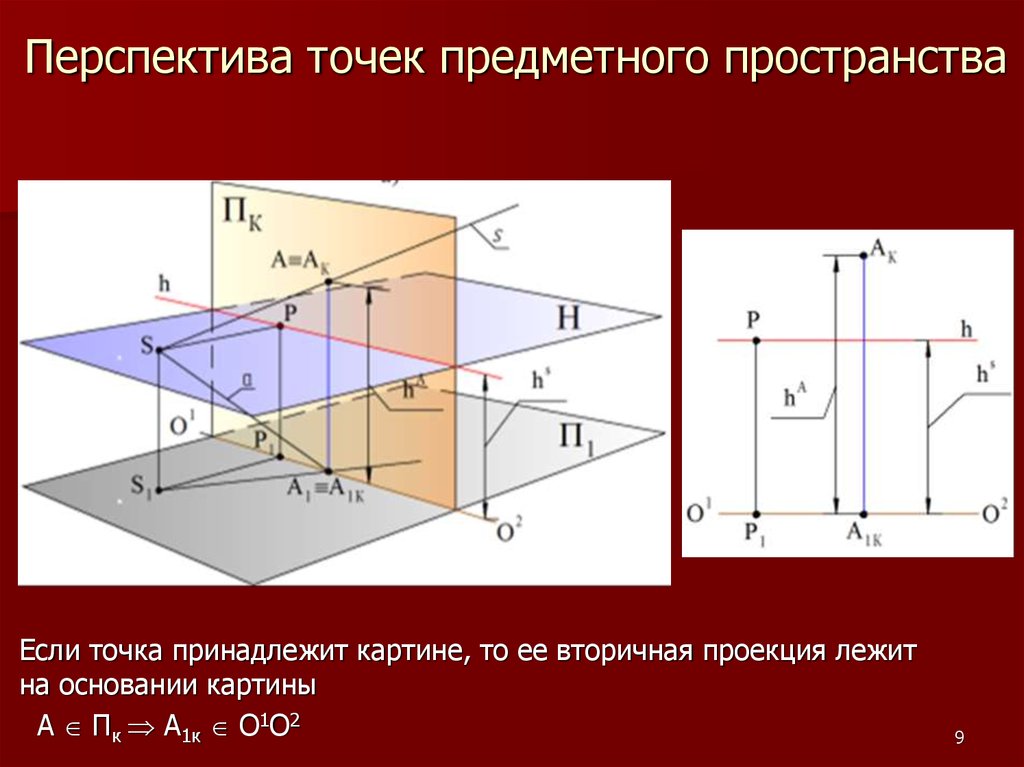
9. Перспектива точек предметного пространства
Если точка принадлежит картине, то ее вторичная проекция лежитна основании картины
А Пк А1к О1О2
9
10.
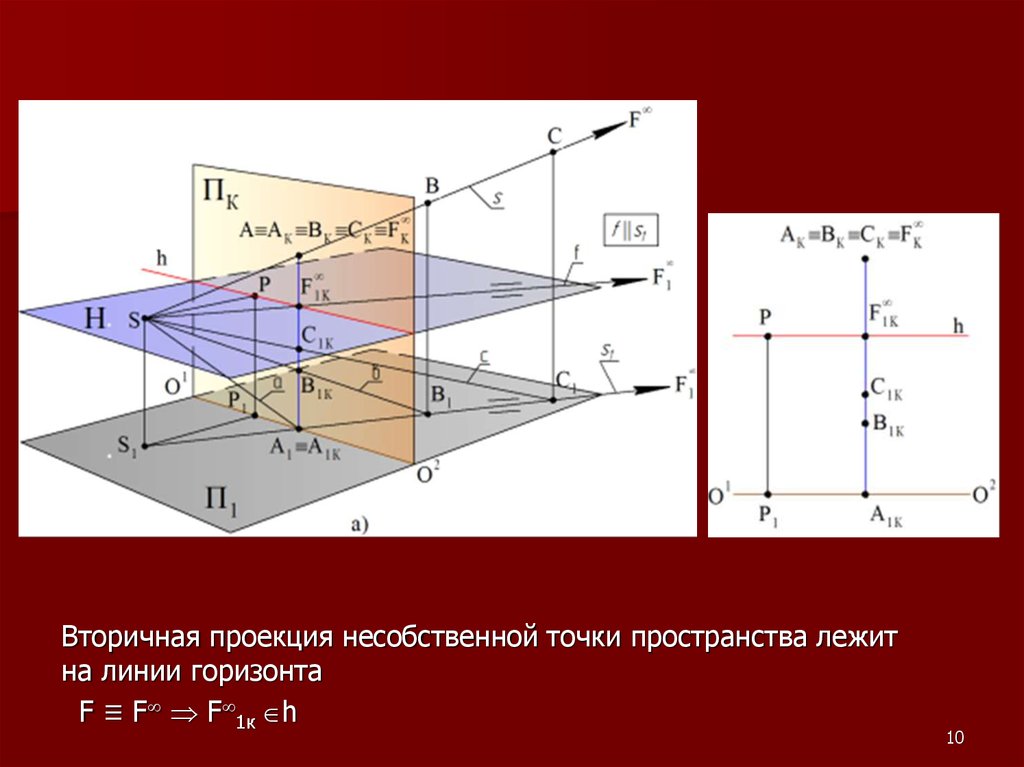
Вторичная проекция несобственной точки пространства лежитна линии горизонта
F ≡ F F 1к h
10
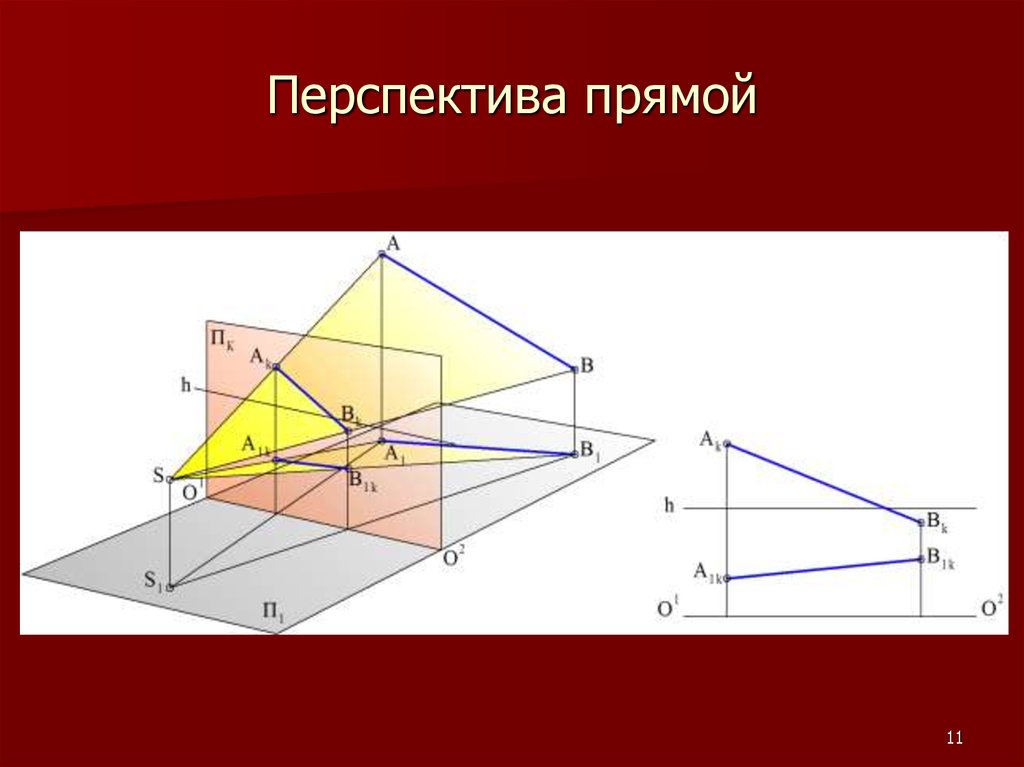
11. Перспектива прямой
1112.
В перспективе прямая(например, m) задается двумя
точками – m (N, F∞).
Точка N – начало прямой.
Принимается точка
пересечения прямой с
картинной плоскостью.
N = m ∩ Пк
Точка F∞ - несобственная
точка.
N Пк Nк ≡ N N1к O1O2;
F∞ F1к h.
13.
14.
F2ks2
S2
N2k
m2
х12
s1
P1
m1
F1k
S1
N1k
Пк1
Чтобы получить (увидеть)
несобственную точку F∞,
принадлежащую прямой m,
находясь в точке зрения S,
необходимо направить луч зрения
параллельно прямой m.
Точка F∞k пересечения луча s с
картинной плоскостью Пk и будет
изображением несобственной точки
F∞.
S s, s II m и s ∩ Пk = F∞k
Чтобы получить точку N начала
прямой m, необходимо продолжить
прямую до пересечения с
картинной плоскостью
m ∩ Пк= N
14
15.
F2ks2
S2
m2
Fk
c
P F1k
d
а
а
m1k
d
s1
P1
m1
O
F1k
b
h
Nk
c
х12
mk
N1k
1
P1
b
O
Пк1
S1
15
2
16.
По положению точки F k относительно линии горизонтаможно судить о положении прямой
m относительно
∞
предметной плоскости.
Если F k выше линии горизонта, то прямая восходящая.
Если F k ниже линии горизонта, то прямая нисходящая.
Если F k лежит на линии горизонта, т.е. F k ≡ F 1k , то прямая
является горизонталью.
FK
h
O
восходящая
mK
нисходящая
h F 1K
Р
F 1K
1
NК
m 1K
FK
2
Р1
а)
N 1К
mK
m 1K
Р1
б)
Р
N 1К
N 1К
д)
Р
h
O
2
O
1
h
Р
m 1K
1
е)
перпендикулярна
картине
F K F 1K Р
h
NК
m 1K
2
O O1
Р1
N 1К
в)
горизонтальнопроецирующая
параллельна
картине
mK
F 1K
m 1K
Р1
m 1K
O O1
?
O
NК
mK
Р
2
O O1
m K F N
K
K
1
F K F 1K
Р
проецирующая
h
горизонталь
2
O
Р1 O Р1 Р1
mK
h
NК
O
г)
mK
m 1K
2
NO
1К
ж)
16
2
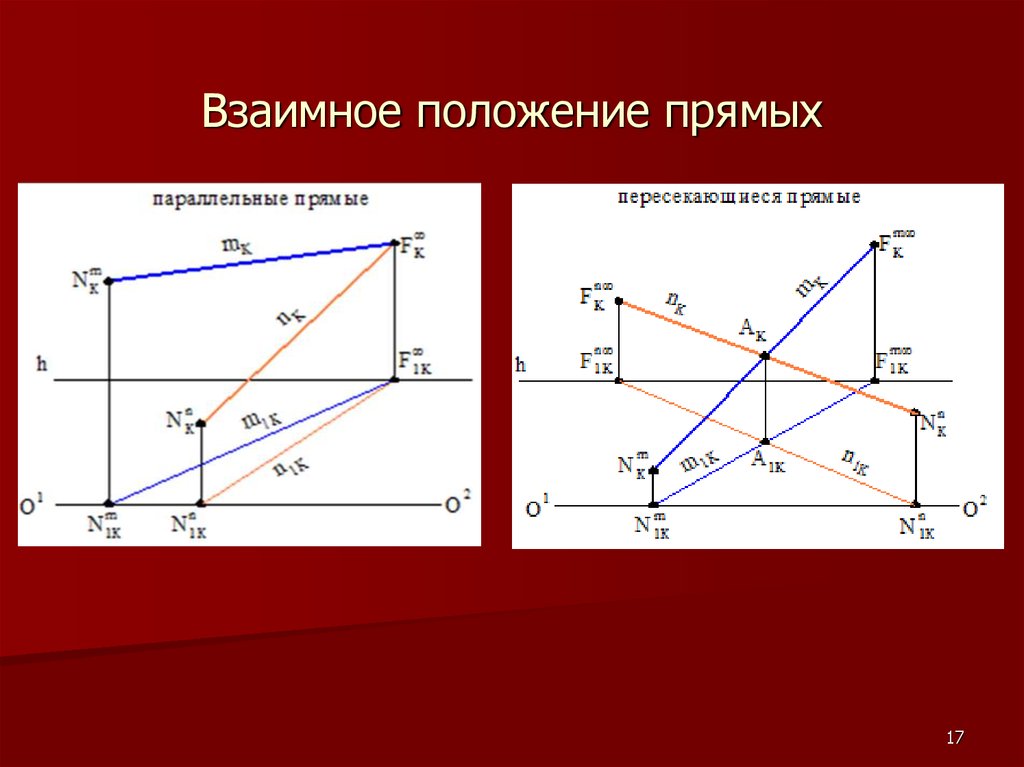
17. Взаимное положение прямых
1718. Деление отрезка в заданном отношении
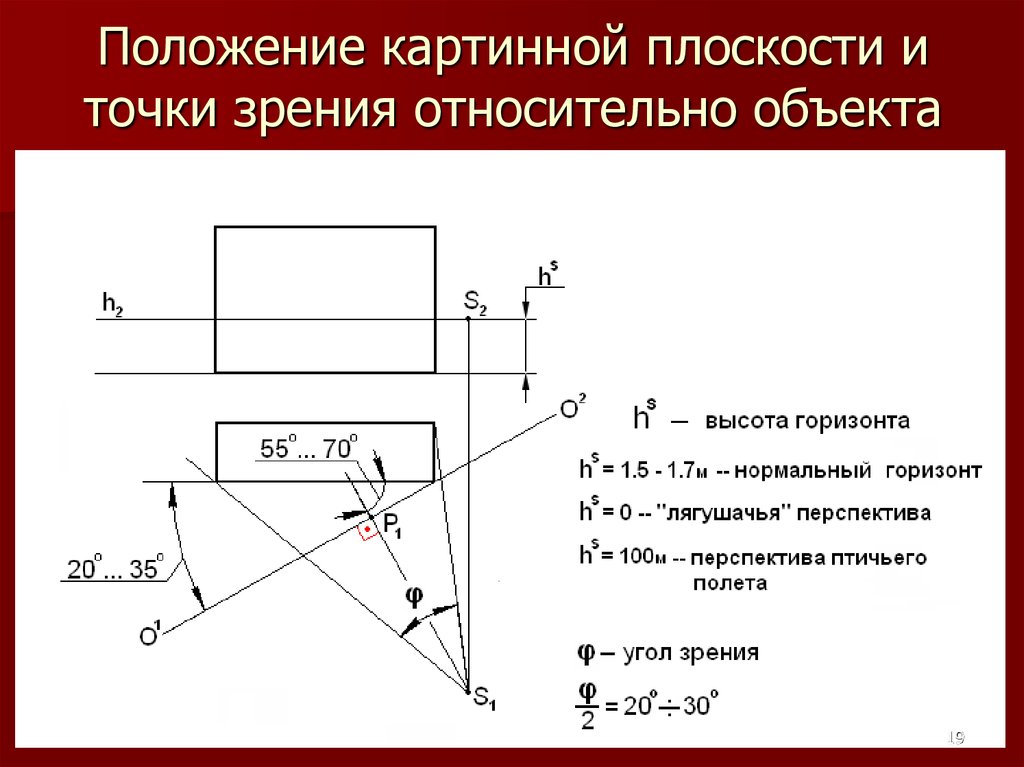
19. Положение картинной плоскости и точки зрения относительно объекта
1920. Способы построения перспективы
2021. Построение перспективы точки
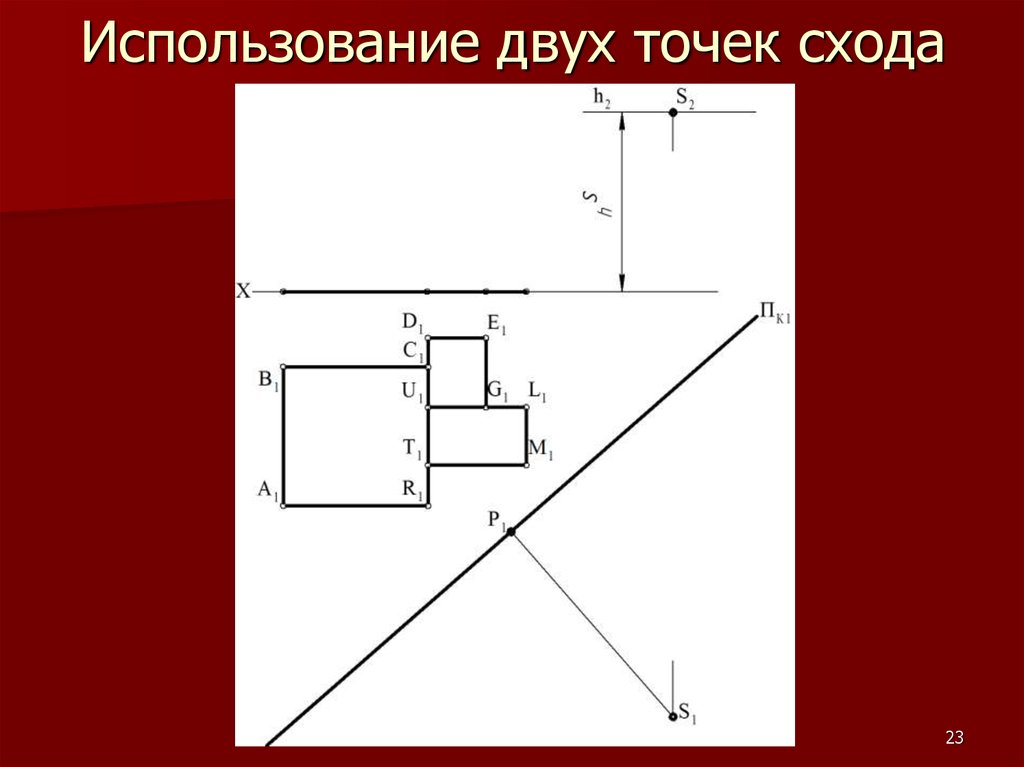
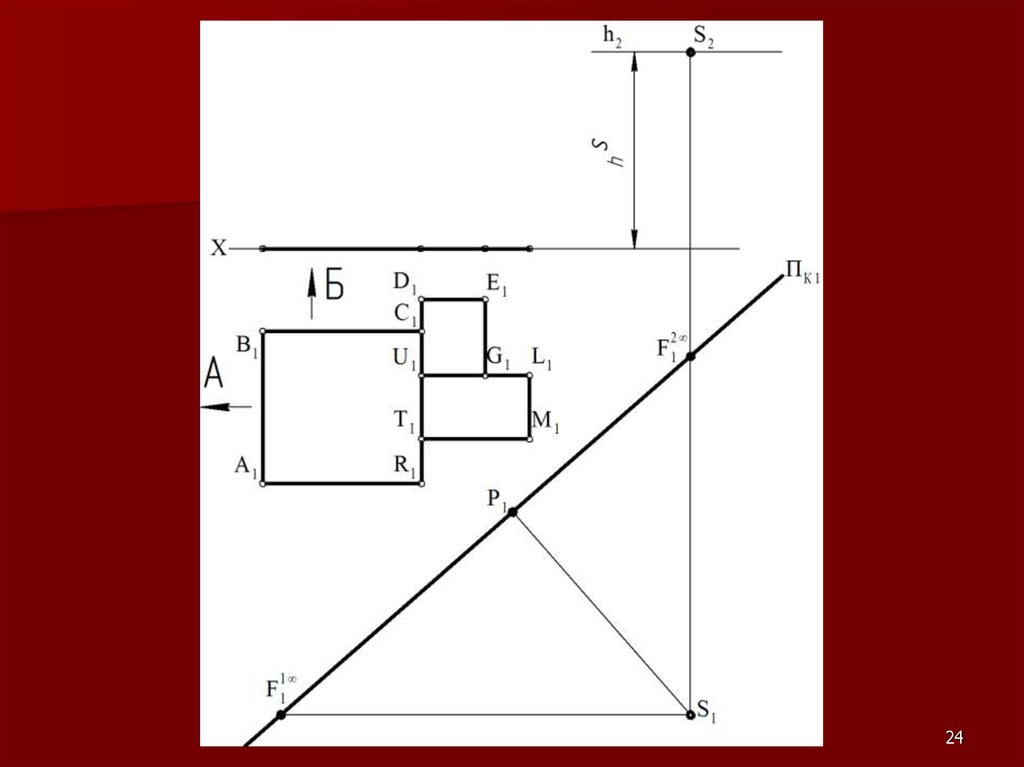
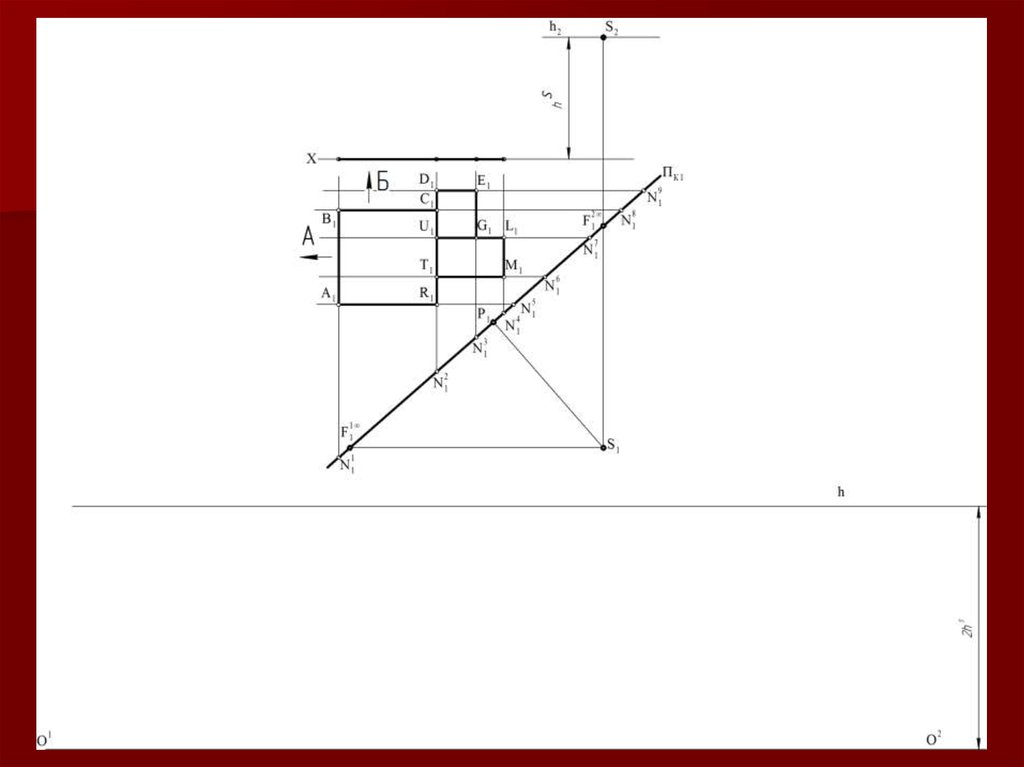
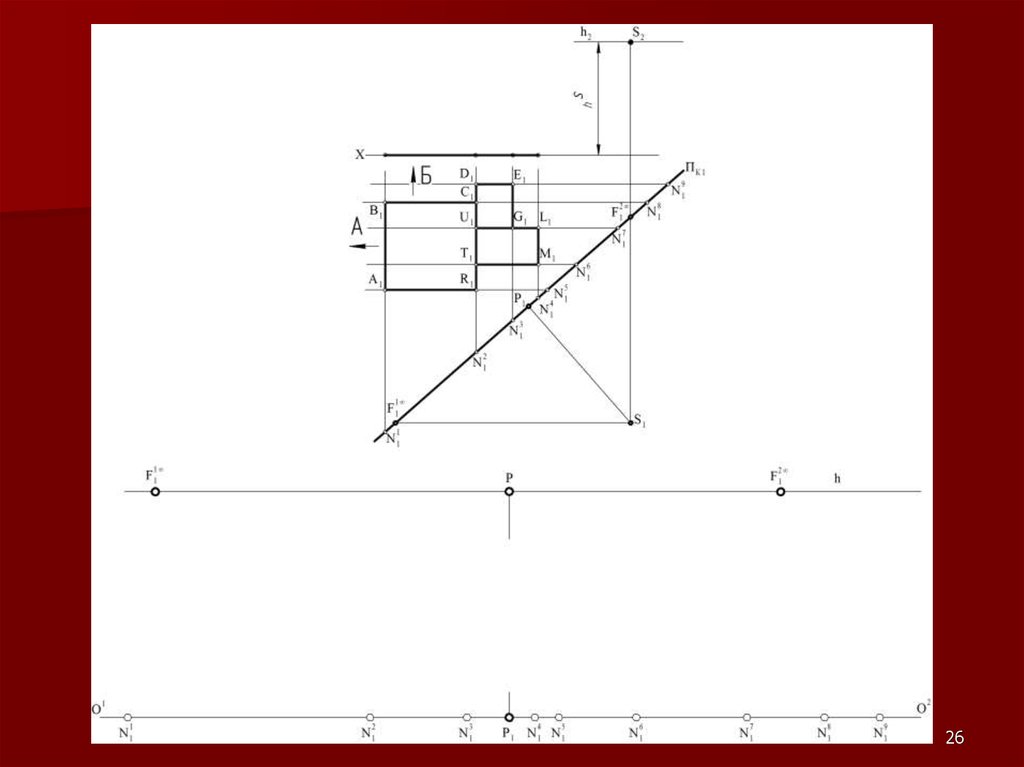
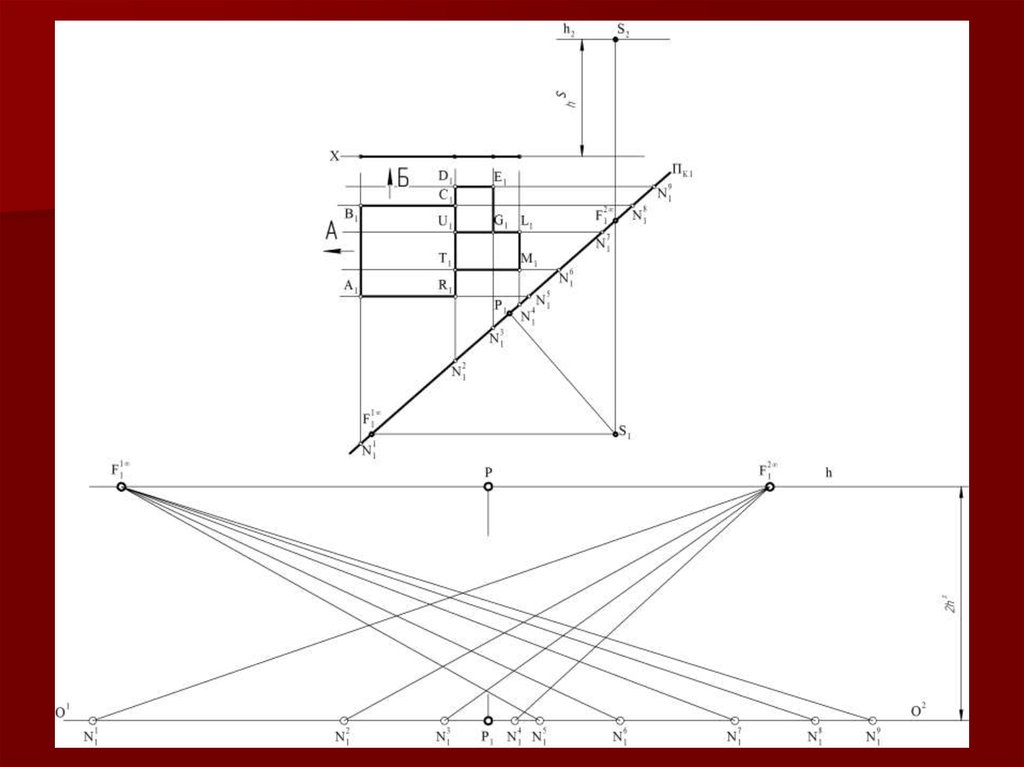
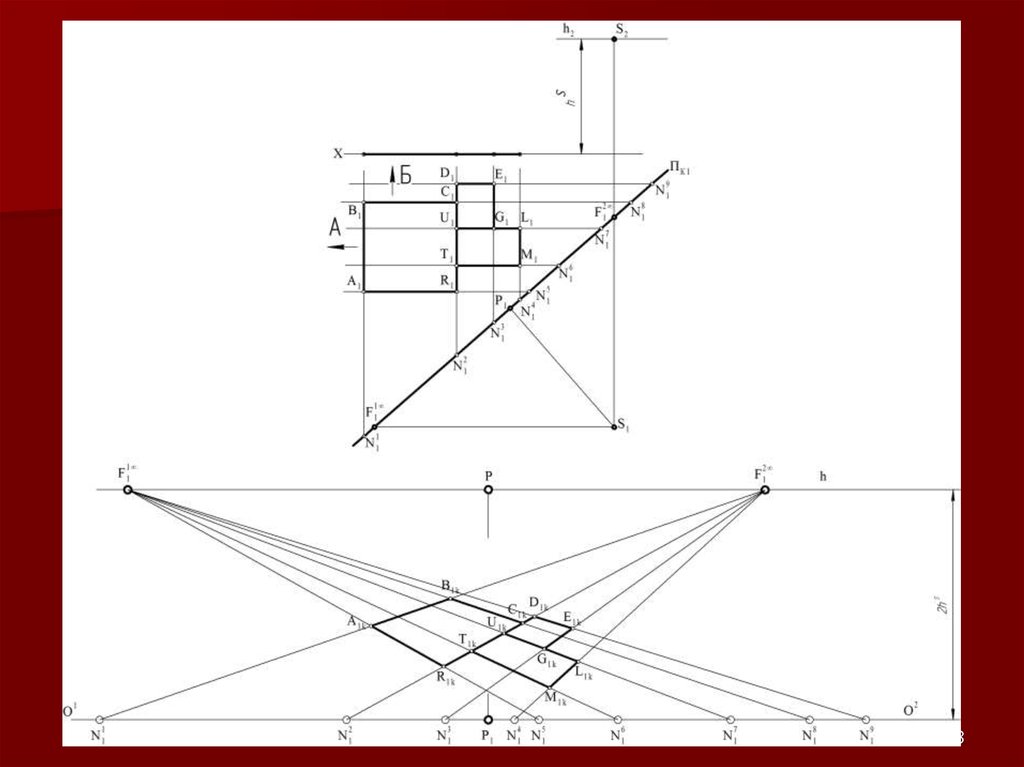
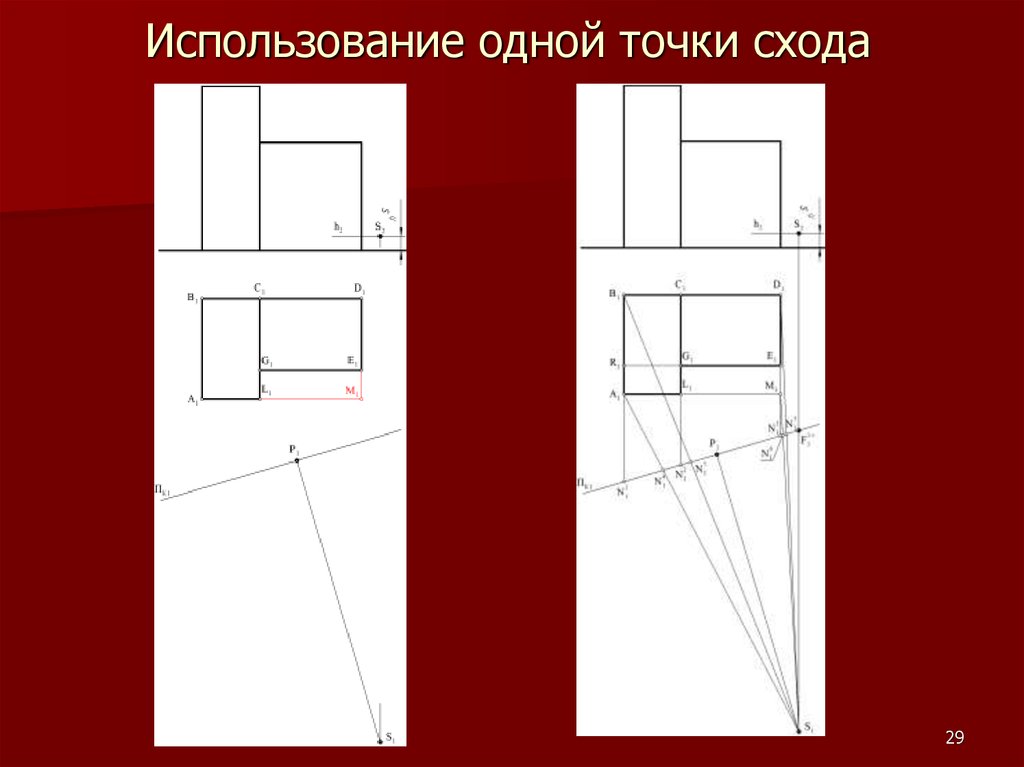
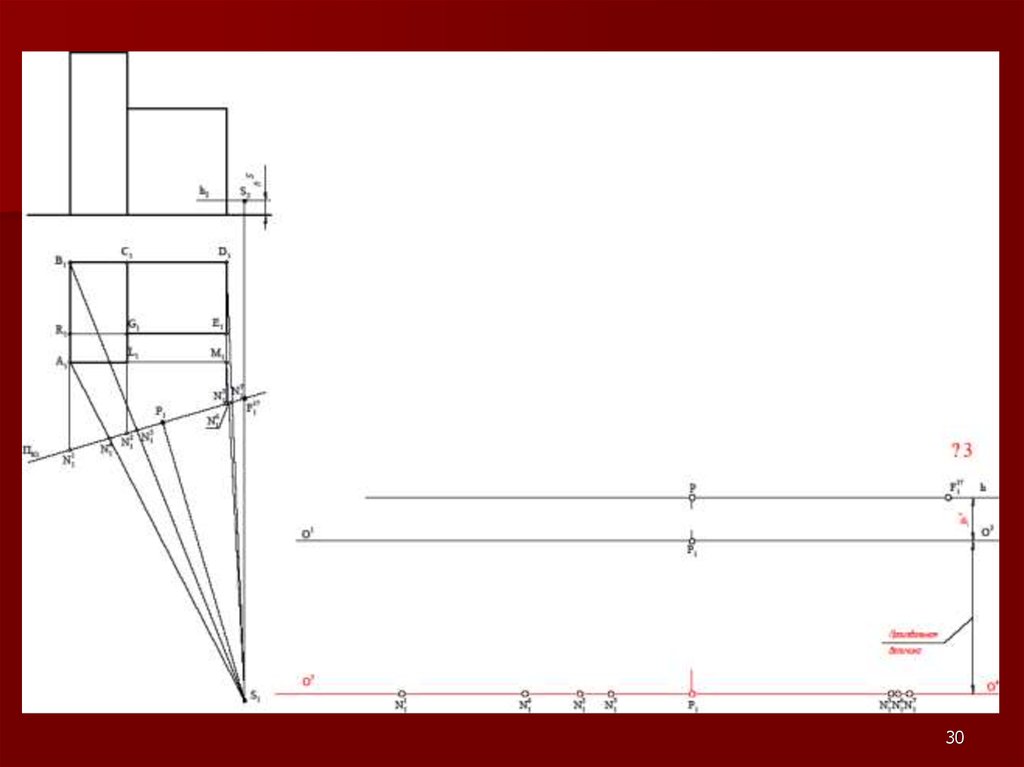
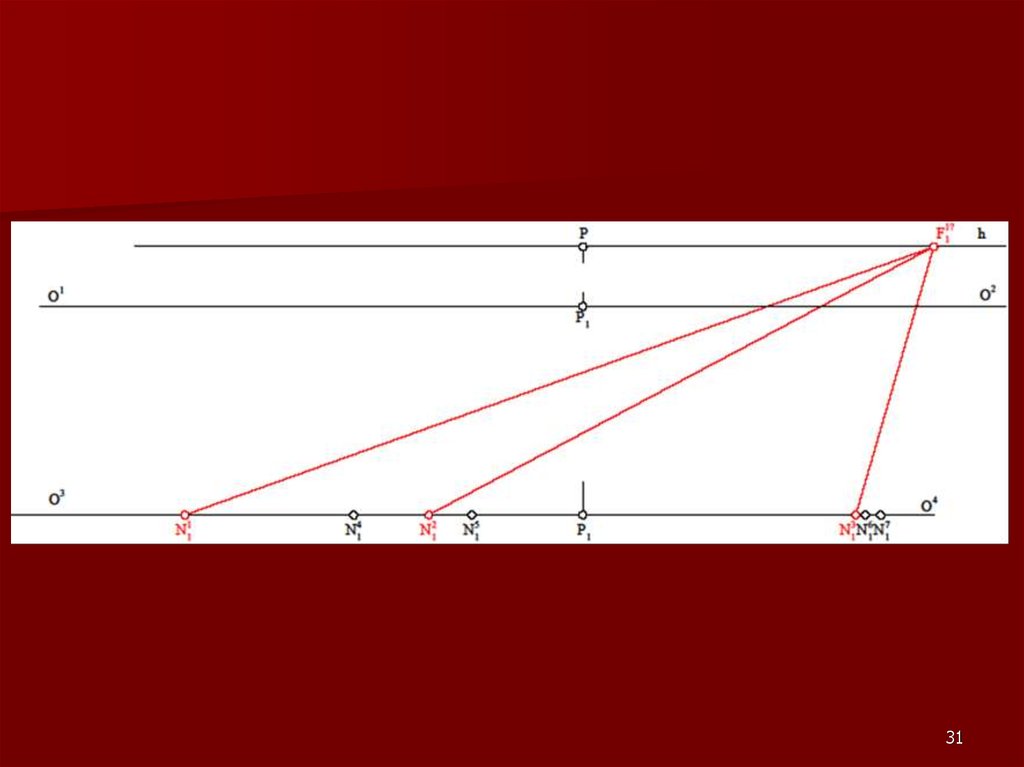
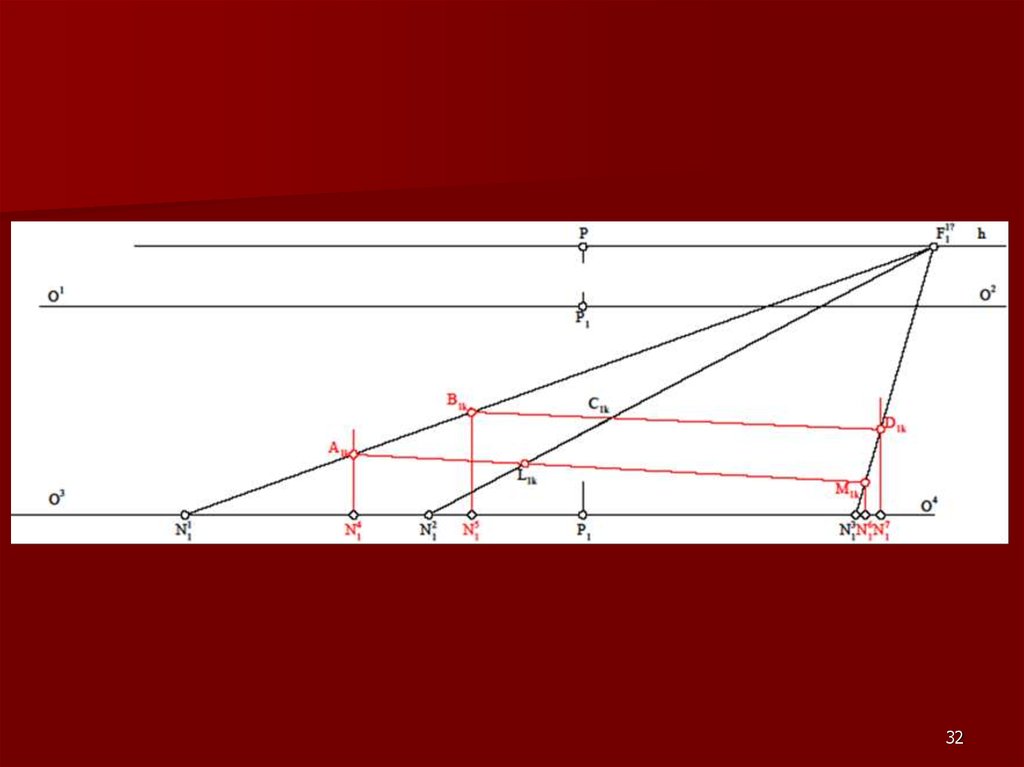
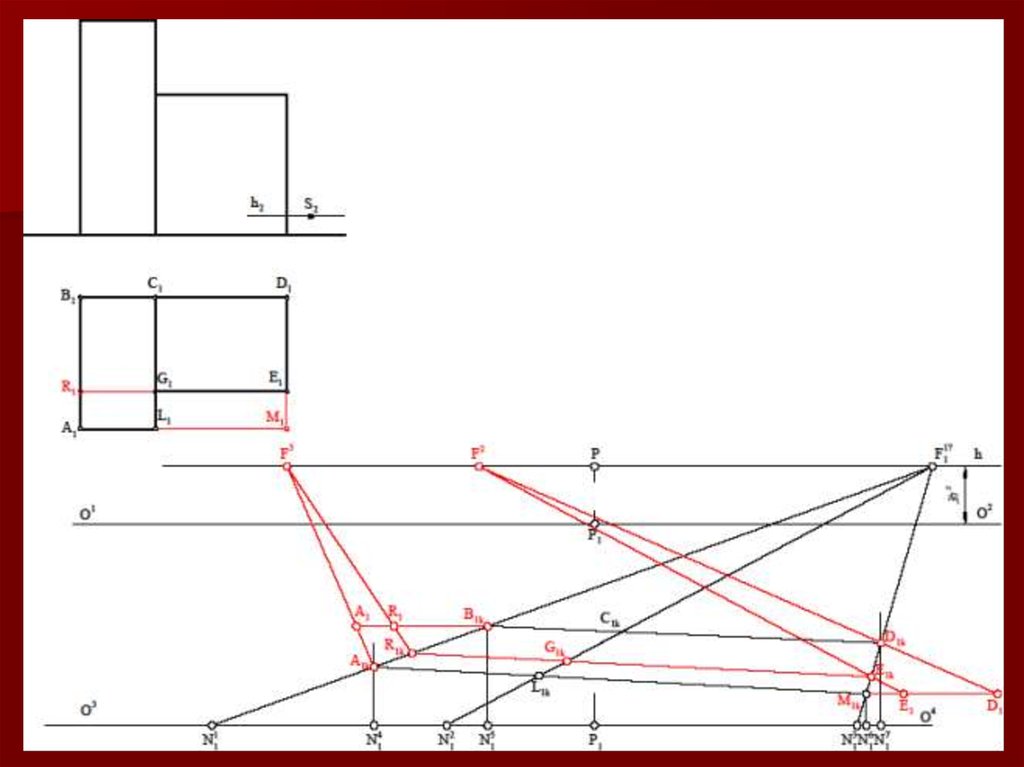
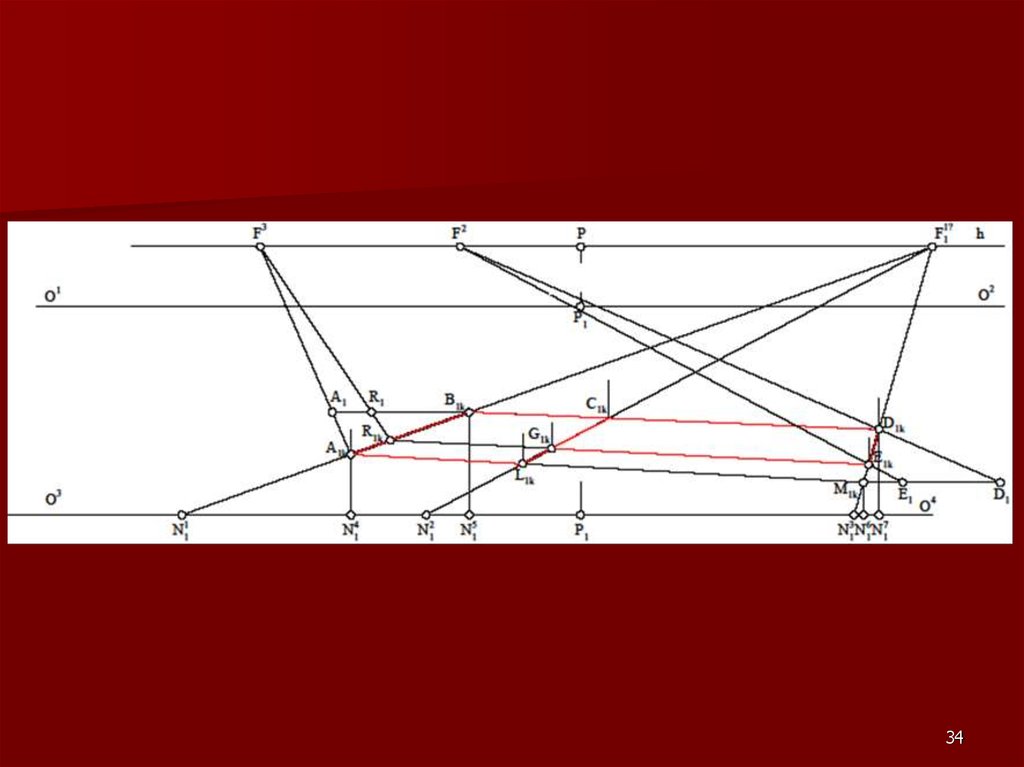
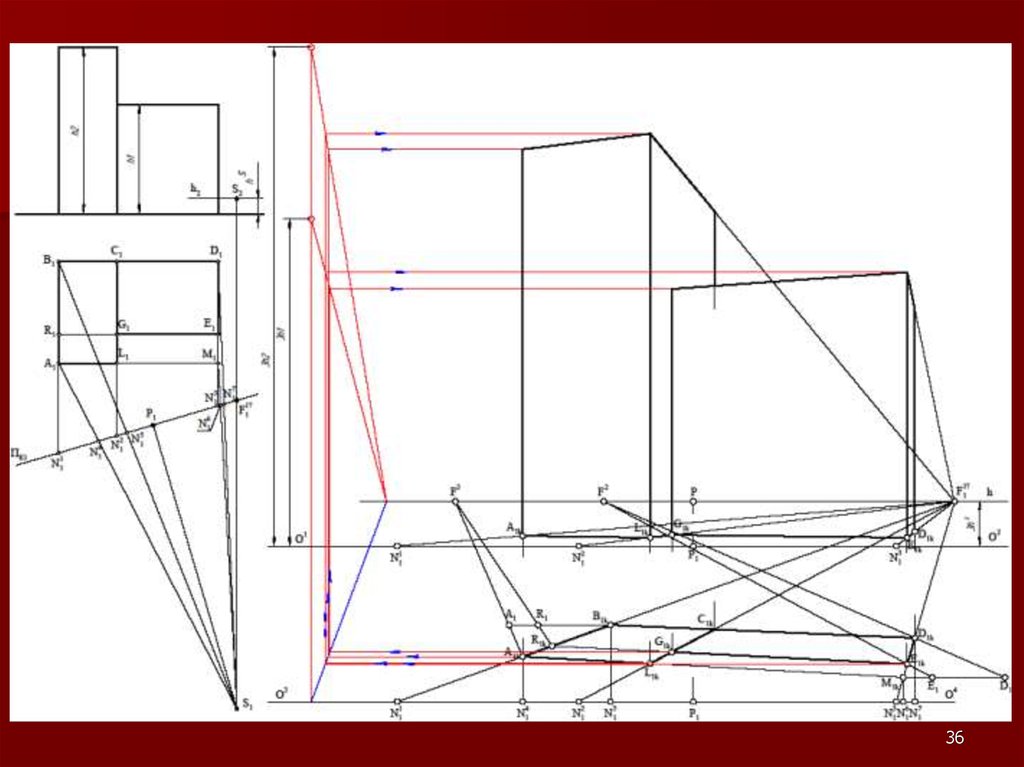
2122. Метод «архитекторов»
Данный метод построения линейнойперспективы основан на использовании
точек схода пучков параллельных между
собой прямых.
22














 drafting
drafting








