Экономические индексы

1.

СТАТИСТИКА
Аналитическая статистика.
Лекция 4. Экономические индексы.
Автор: Равичев Л.В..
РХТУ им. Д.И.Менделеева
Кафедра управления технологическими инновациями
Москва - 2013

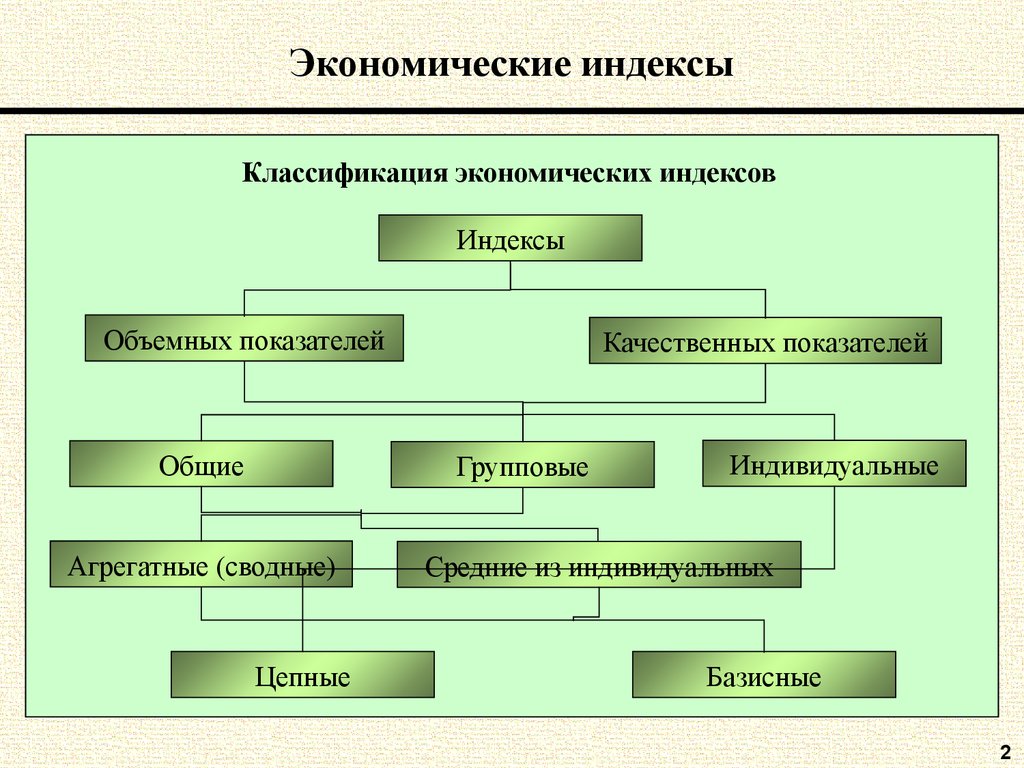
2. Экономические индексы

Классификация экономических индексов
Индексы
Объемных показателей
Общие
Качественных показателей
Групповые
Агрегатные (сводные)
Цепные
Индивидуальные
Средние из индивидуальных
Базисные
2

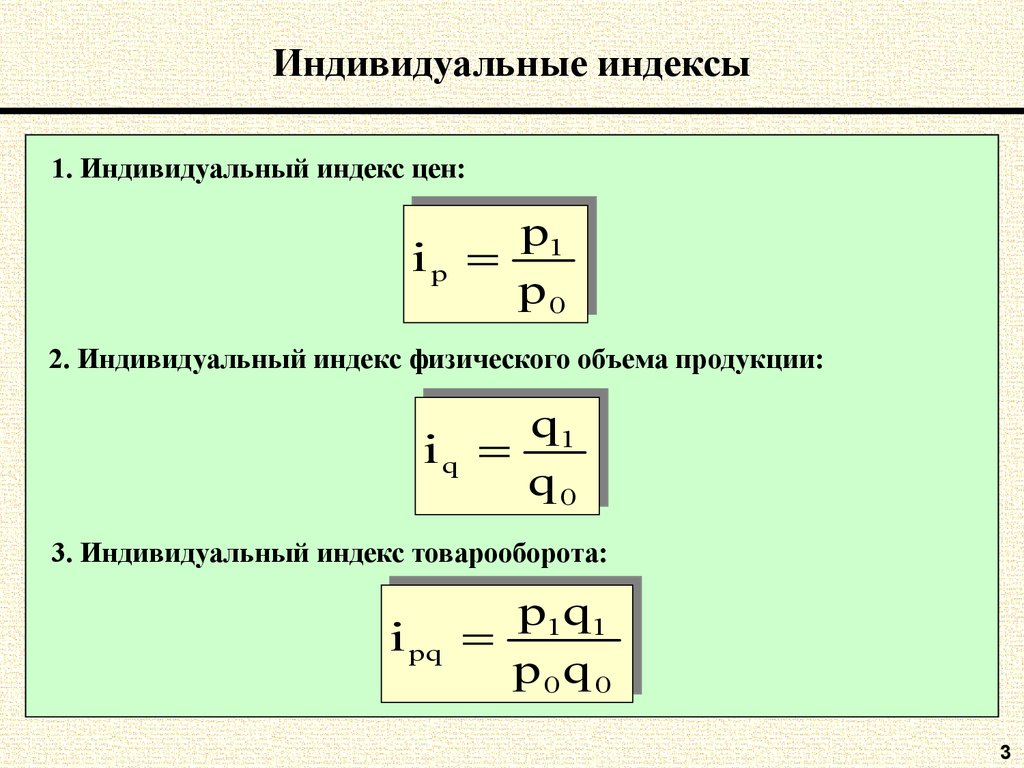
3. Индивидуальные индексы

1. Индивидуальный индекс цен:
p11
p
iipp
pp00
2. Индивидуальный индекс физического объема продукции:
q11
q
iiqq
qq00
3. Индивидуальный индекс товарооборота:
p11qq11
p
iipq
pq
pp00qq00
3

4. Индивидуальные индексы

4. Индивидуальный индекс себестоимости:
z11
z
iizz
zz00
5. Индивидуальный индекс производительности труда:
w11
w
iiww
w00
w
q00
q11
q
q
w11 ;; w
w00
w
TT11
TT00
4

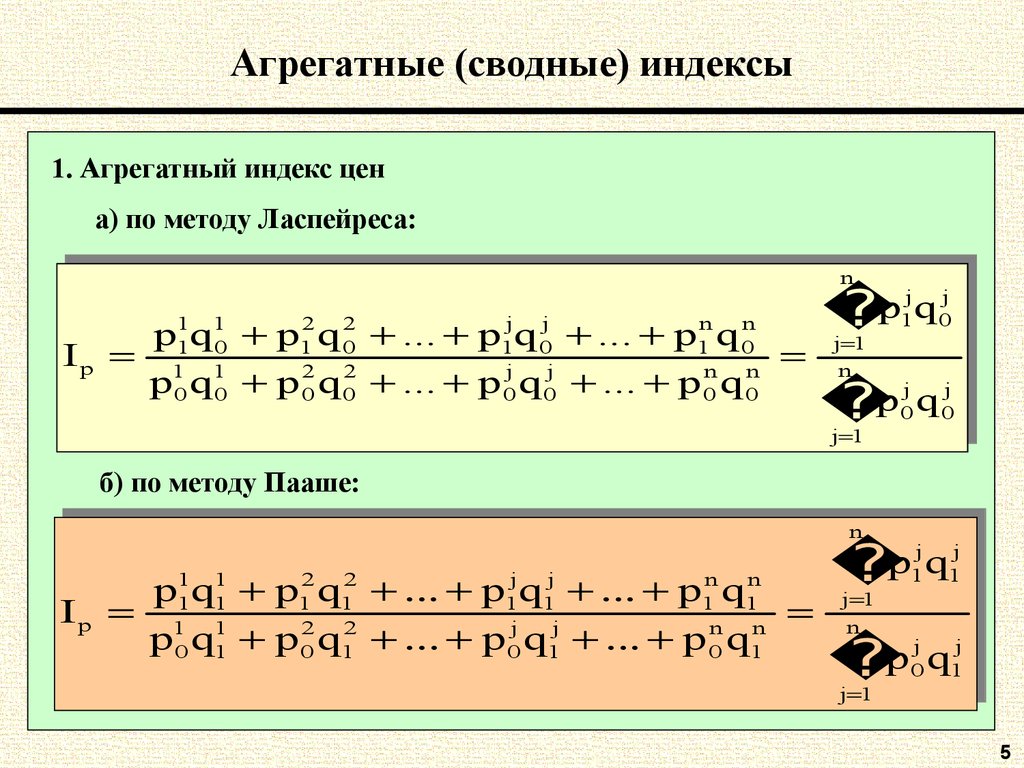
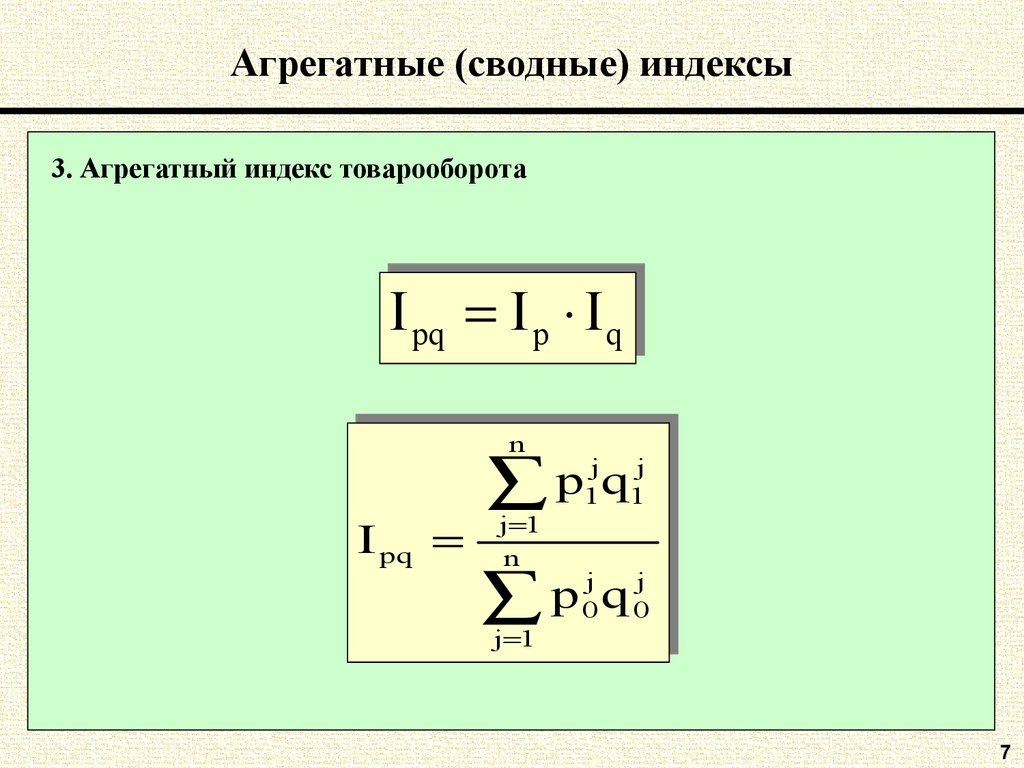
5. Агрегатные (сводные) индексы

1. Агрегатный индекс цен
а) по методу Ласпейреса:
nn
11q11 p22 q22 ... pj jqj j ... pnn qnn
p
p11q 00 p11q 00 ... p11q 00 ... p11q 00
I
I pp 11 11
22 q22 ... pj j qj j ... pnn qnn
p
q
p
p 0q 0 p 0q 0 ... p 0q 0 ... p 0q 0
0
0
0
0
0
0
0
0
j jqj j
p
p11q 00
j
j
11
nn
j j qj j
p
p 00q 00
j
j
11
б) по методу Пааше:
nn
11q11 p22 q22 ... pj jqj j ... pnn qnn
p
p11q11 p11q11 ... p11q11 ... p11q11
I
I pp 11 11
22 q22 ... pj j qj j ... pnn qnn
p
q
p
p 0q 1 p 0q 1 ... p 0q 1 ... p 0q 1
0
1
0
1
0
1
0
1
j jqj j
p
p11q11
j
j
11
nn
j j qj j
p
p 00q11
j
j
11
5

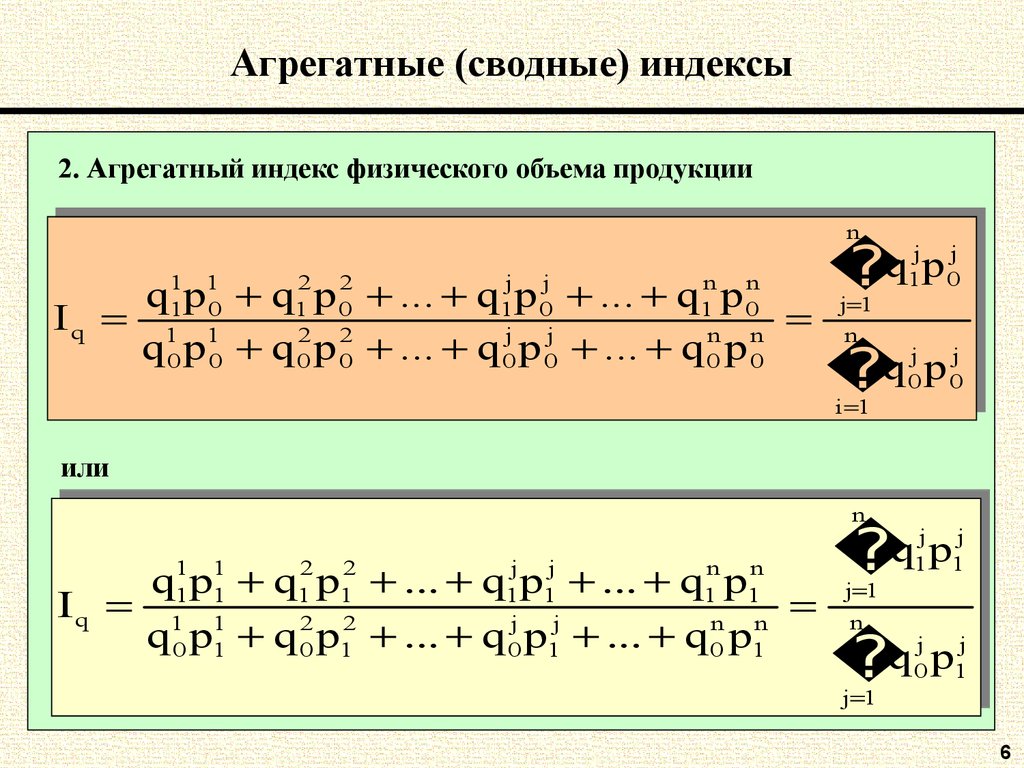
6. Агрегатные (сводные) индексы

2. Агрегатный индекс физического объема продукции
nn
11p11 q22 p22 ... qj j pj j ... qnn pnn
q
q11p 00 q11p 00 ... q11p 00 ... q11p 00
I
I qq 11 11
22 p22 ... qj j pj j ... qnn pnn
q
p
q
q 00p 00 q 00p 00 ... q 00p 00 ... q 00p 00
j j pj j
q
q11p00
j
j
11
nn
j j pj j
q
q 00p00
i i
11
или
nn
11p11 q22 p22 ... qjj pj j ... qnn pnn
q
q11p11 q11p11 ... q11p11 ... q11p11
I
I qq 11 11
2 22
j jj
n nn
2
j
n
... qq00pp11 ...
... qq00pp11
qq00pp11 qq00pp11 ...
j j pj j
q
q11p11
j 11
j
nn
j j pj j
q
q 00p11
j 11
j
6

7. Агрегатные (сводные) индексы

3. Агрегатный индекс товарооборота
IIpqpq IIpp IIqq
nn
IIpq
pq
pp qq
jj 11
nn
jj jj
11 11
jj qjj
p
p 00q 00
jj 11
7

8. Агрегатные (сводные) индексы

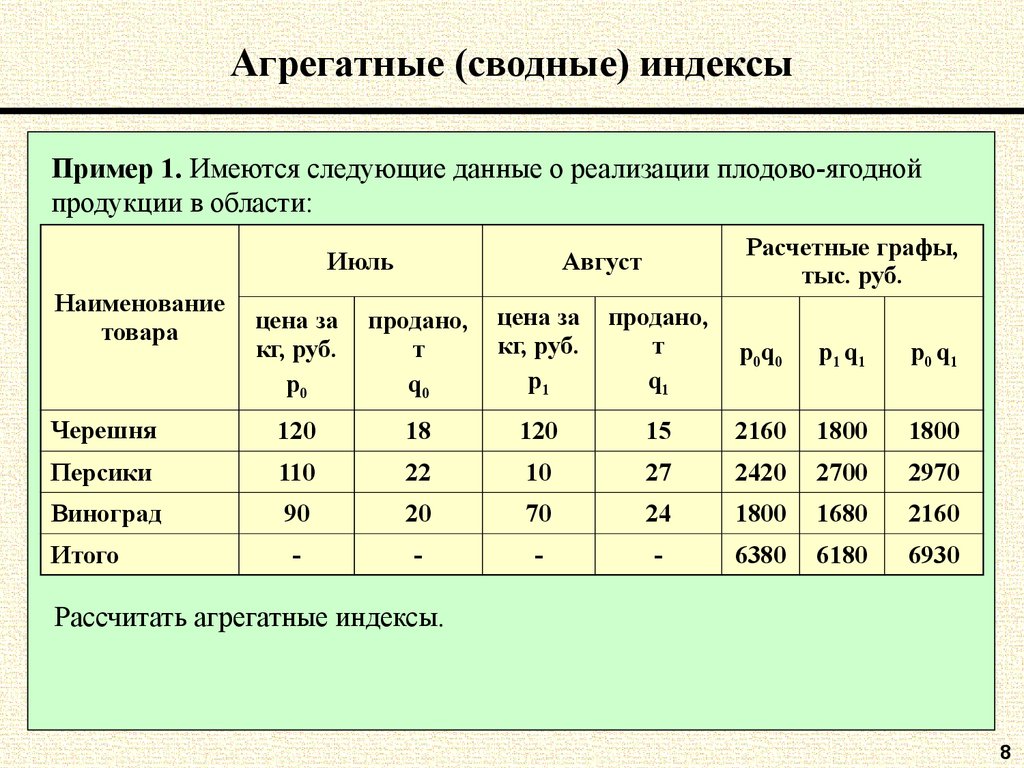
Пример 1. Имеются следующие данные о реализации плодово-ягодной
продукции в области:
Июль
Наименование
товара
Расчетные графы,
тыс. руб.
Август
цена за
кг, руб.
p0
продано,
т
q0
цена за
кг, руб.
p1
продано,
т
q1
p0q0
p1 q1
p0 q1
Черешня
120
18
120
15
2160
1800
1800
Персики
110
22
10
27
2420
2700
2970
Виноград
90
20
70
24
1800
1680
2160
-
-
-
-
6380
6180
6930
Итого
Рассчитать агрегатные индексы.
8

9. Агрегатные (сводные) индексы

Решение.
1. Индекс товарооборота:
n
I pq
p q
j 1
n
j
1
p
j 1
j
0
j
1
q 0j
6180
0,969 или 96,9%
6380
2. Индекс цен:
n
Ip
p q
j 1
n
p
j 1
j
1
j
0
j
1
q1j
6180
0,892 или 89,2%
6930
9

10. Агрегатные (сводные) индексы

3. Величина экономии (перерасхода) покупателей от изменения цен:
n
n
j 1
j 1
E p1jq1j p 0j q1j 6180 - 6930 750
4. Индекс физического объема продукции:
n
Iq
j
j
q
p
1 0
j 1
n
j
j
q
p
0 0
6930
1,086 или 108,6%.
6380
j 1
Проверка:
I pq I p I q 0,892 1,086 0,969 или 96,9%.
10

11. Агрегатные (сводные) индексы

4. Индекс себестоимости:
nn
IIpq
pq
jjqjj
z
z11q11
jj 11
nn
jj qjj
z
z 00q11
jj 11
Сумма экономии предприятия от снижения себестоимости:
nn
nn
E
E
zz qq
zz qq
11
jj
jj
11
jj
11
11
jj
jj
00
jj
11
11

12. Агрегатные (сводные) индексы

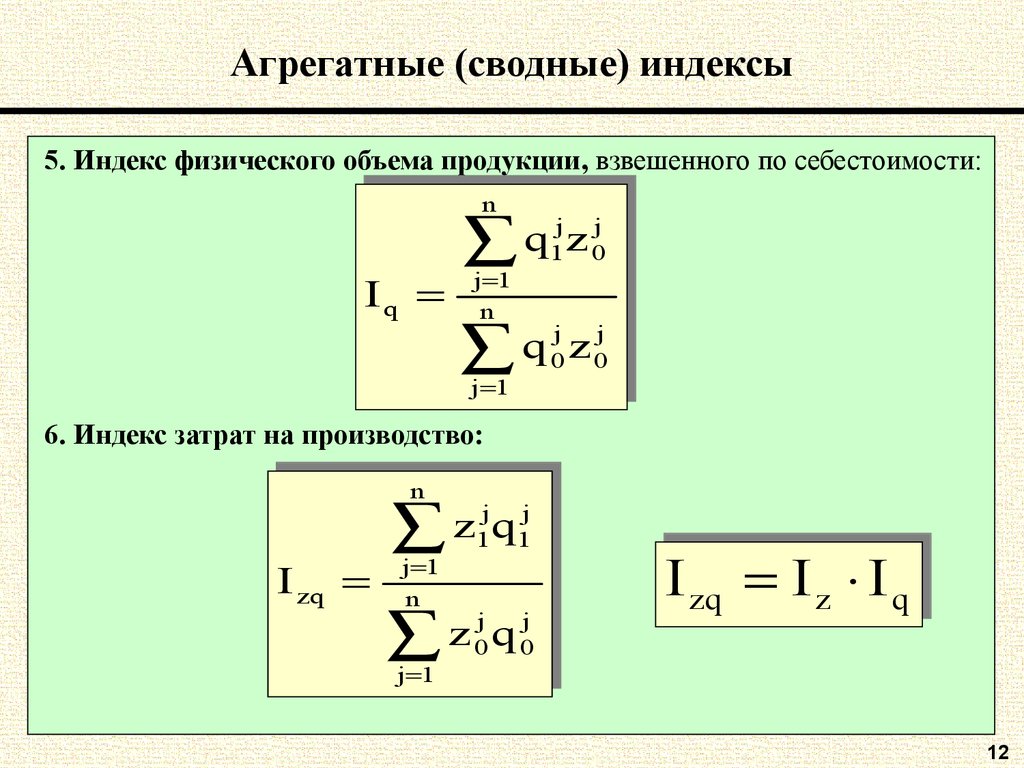
5. Индекс физического объема продукции, взвешенного по себестоимости:
nn
IIqq
jj zjj
q
q11z 00
j 11
j
nn
jj zjj
q
q 00z 00
j 11
j
6. Индекс затрат на производство:
nn
IIzq
zq
jjqjj
z
z11q11
j 11
j
nn
jj qjj
z
z 00q 00
IIzqzq IIzz IIqq
j 11
j
12

13. Агрегатные (сводные) индексы

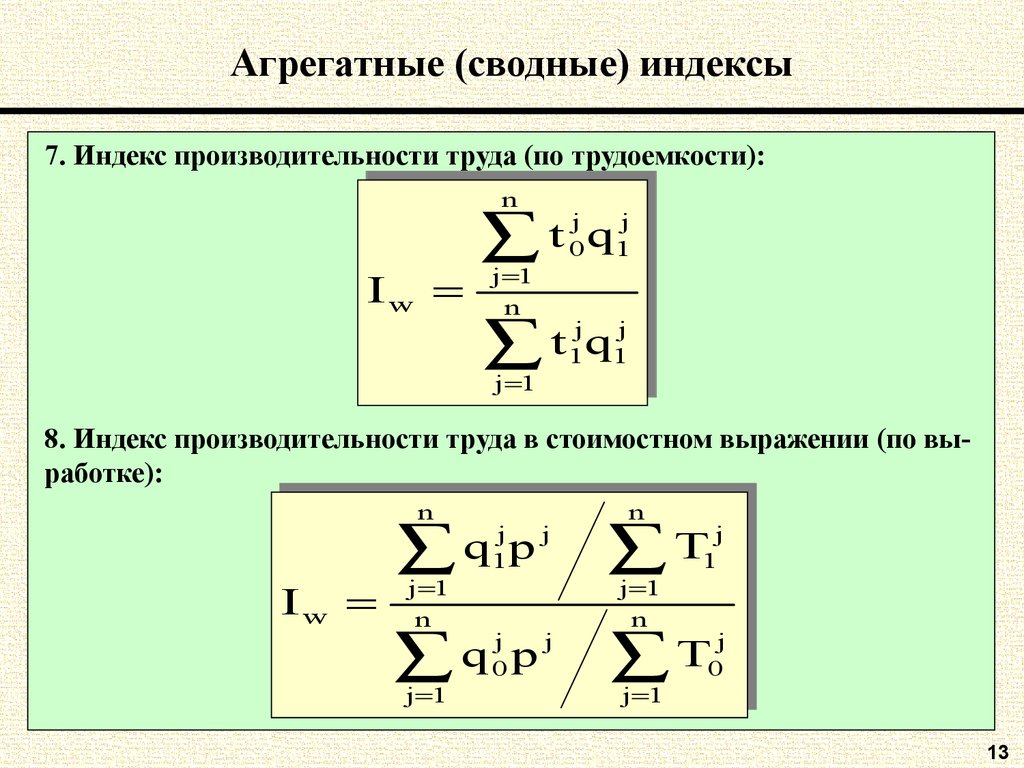
7. Индекс производительности труда (по трудоемкости):
nn
IIww
jj qjj
t
t 00q11
jj 11
nn
jjqjj
t
t11q11
jj 11
8. Индекс производительности труда в стоимостном выражении (по выработке):
nn
IIww
nn
jj pjj
q
q11p
jj
T
T11
jj pjj
q
q 00p
jj
T
T00
jj 11
nn
jj 11
jj 11
nn
jj 11
13

14. Агрегатные (сводные) индексы

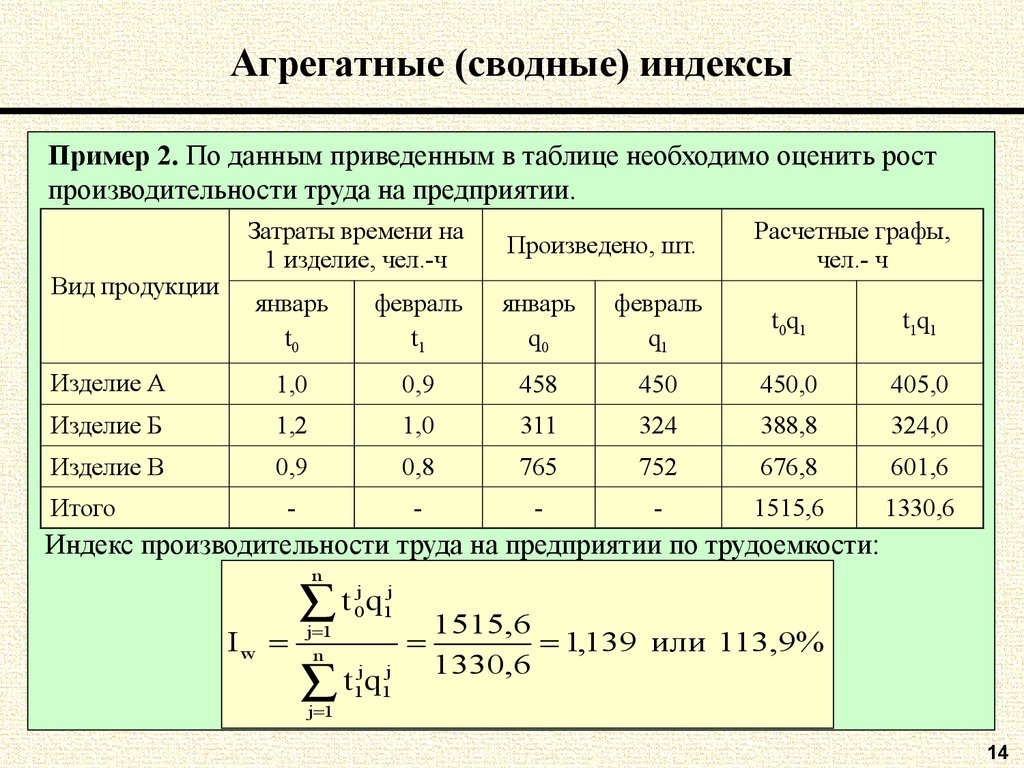
Пример 2. По данным приведенным в таблице необходимо оценить рост
производительности труда на предприятии.
Вид продукции
Затраты времени на
1 изделие, чел.-ч
Произведено, шт.
Расчетные графы,
чел.- ч
январь
t0
февраль
t1
январь
q0
февраль
q1
t0q1
t1q1
Изделие А
1,0
0,9
458
450
450,0
405,0
Изделие Б
1,2
1,0
311
324
388,8
324,0
Изделие В
0,9
0,8
765
752
676,8
601,6
-
-
-
-
1515,6
1330,6
Итого
Индекс производительности труда на предприятии по трудоемкости:
n
Iw
j
j
t
q
0 1
j 1
n
j j
t
1q1
1515,6
1,139 или 113,9%
1330,6
j 1
14

15. Агрегатные (сводные) индексы

Пример 3. Имеются следующие данные о производстве продукции и
средних отпускных ценах продукции предприятия:
Январь
Вид
продукции
произв
едено,
шт.
q0
Февраль
трудовые
затраты,
чел.-ч
Т0
произв
едено,
шт.
q1
трудовы
е
затраты,
чел.-ч
Т1
Средня
я
отпускн
ая цена,
руб.
р
Изделие А
458
458,0
450
405,0
Изделие Б
311
373,2
324
324,0
240
200
252
210
216
Изделие В
765
688,5
752
601,6
180
Расчетные графы,
руб
q0p
q1 p
109920
91600
78372
108000
90000
81648
68040
162432
65310
165240
137700
353532
Итого
1519,7
1330,6
294610
Индекс
производительности
труда на
предприятии
по- выработке:
n
Iw
q p
j 1
n
q
j 1
j
1
j
0
j
pj
n
T
j 1
n
j
1
T
j 1
j
0
135360
352080
293400
352080
293400 1330,6 264
220,60
50
1,137 или 113,7%
353532
294610 1519,7 193
232,86
63
15

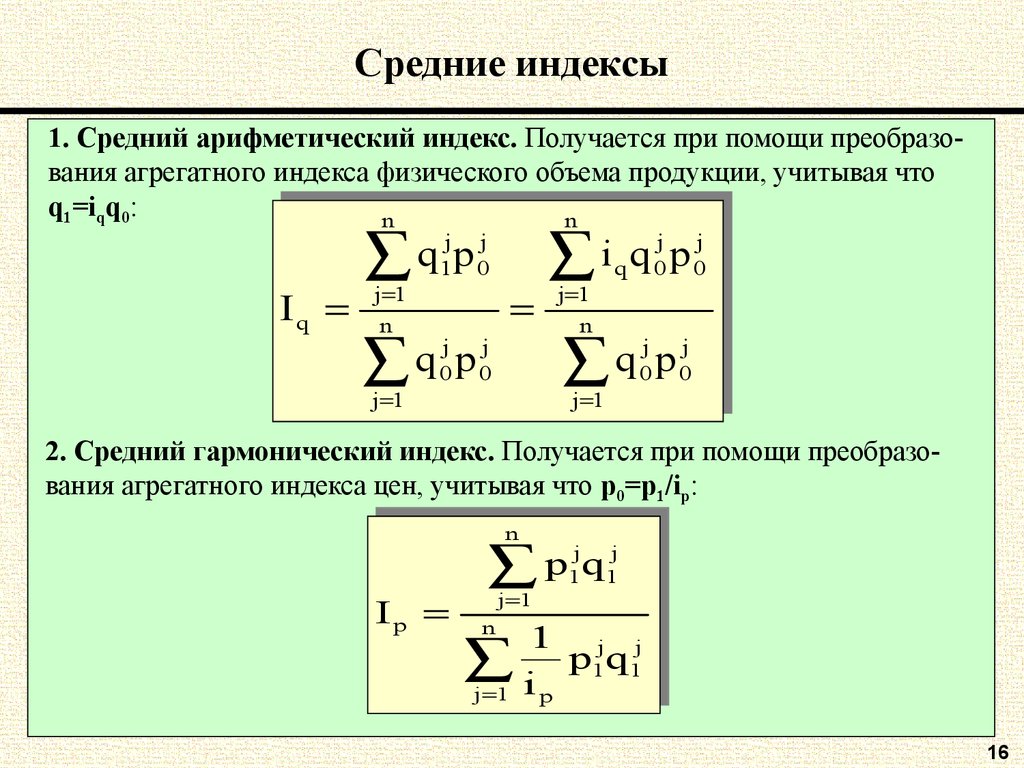
16. Средние индексы

1. Средний арифметический индекс. Получается при помощи преобразования агрегатного индекса физического объема продукции, учитывая что
q1=iqq0:
nn
nn
IIqq
j j pj j
q
q11p 00
j 11
j
nn
j j pj j
q
q 00p 00
j 11
j
j j pj j
i
q
i qqq 00p 00
j 11
j
nn
j j pj j
q
q 00p 00
j 11
j
2. Средний гармонический индекс. Получается при помощи преобразования агрегатного индекса цен, учитывая что p0=p1/ip:
nn
IIpp
j jqj j
p
p11q11
j
j
11
nn
11 pjjqjj
p11q11
i
j
j
11 i pp
16

17. Средние индексы

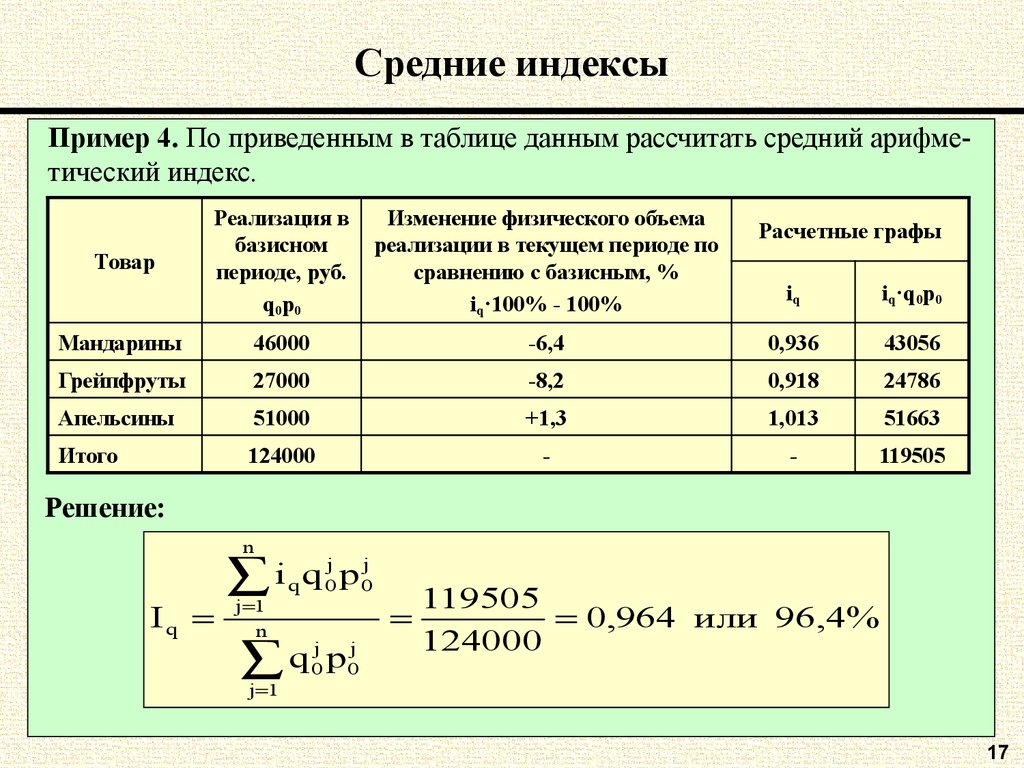
Пример 4. По приведенным в таблице данным рассчитать средний арифметический индекс.
Реализация в
базисном
периоде, руб.
q0p0
Изменение физического объема
реализации в текущем периоде по
сравнению с базисным, %
iq·100% - 100%
Мандарины
46000
Грейпфруты
Товар
Расчетные графы
iq
iq·q0p0
-6,4
0,936
43056
27000
-8,2
0,918
24786
Апельсины
51000
+1,3
1,013
51663
Итого
124000
-
-
119505
Решение:
n
Iq
i
j 1
n
q
q 0j p 0j
j
j
q
p
0 0
119505
0,964 или 96,4%
124000
j 1
17

18. Средние индексы

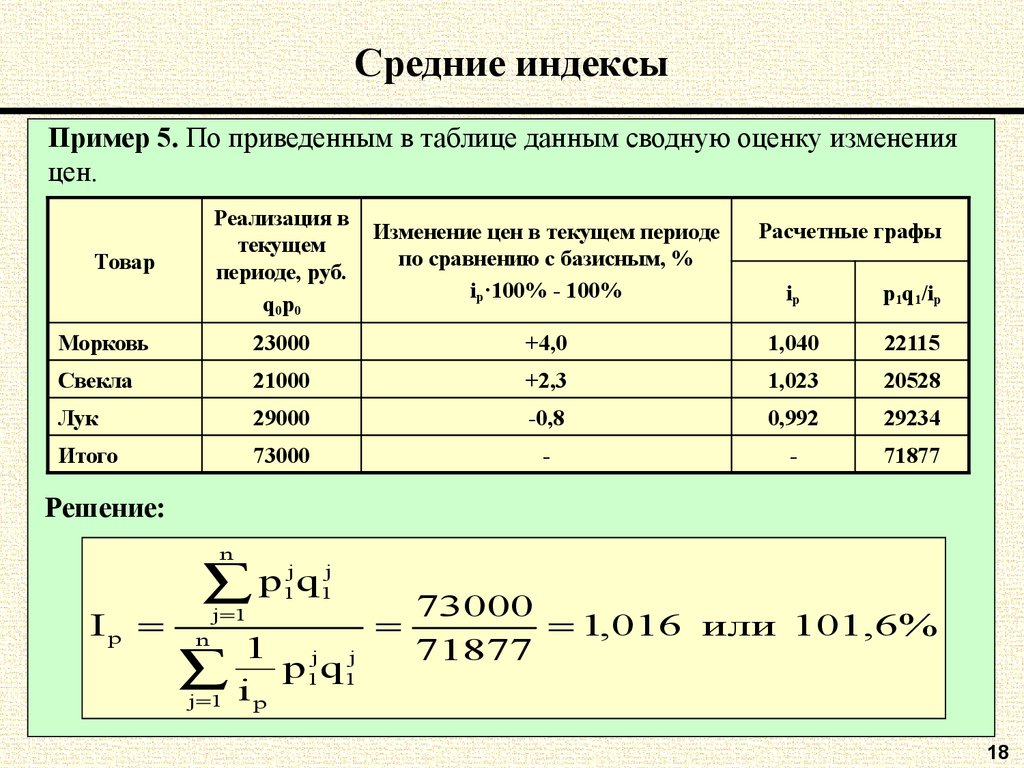
Пример 5. По приведенным в таблице данным сводную оценку изменения
цен.
Реализация в
текущем
периоде, руб.
q0p0
Изменение цен в текущем периоде
по сравнению с базисным, %
ip·100% - 100%
Морковь
23000
Свекла
Товар
Расчетные графы
ip
p1q1/ip
+4,0
1,040
22115
21000
+2,3
1,023
20528
Лук
29000
-0,8
0,992
29234
Итого
73000
-
-
71877
Решение:
n
Ip
j
j
p
q
1 1
j 1
n
1 j j
p1q1
j 1 i p
73000
1,016 или 101,6%
71877
18

19. Средние индексы

3. Средний арифметический индекс производительности труда по
трудоемкости (индекс Струмилина):
jj
jj
T
T
T00 : T11 Tjj
qjj : qjj T11
jj 11 q 00 q11
nn
IIww
nn
jj
T
T11
jj 11
19

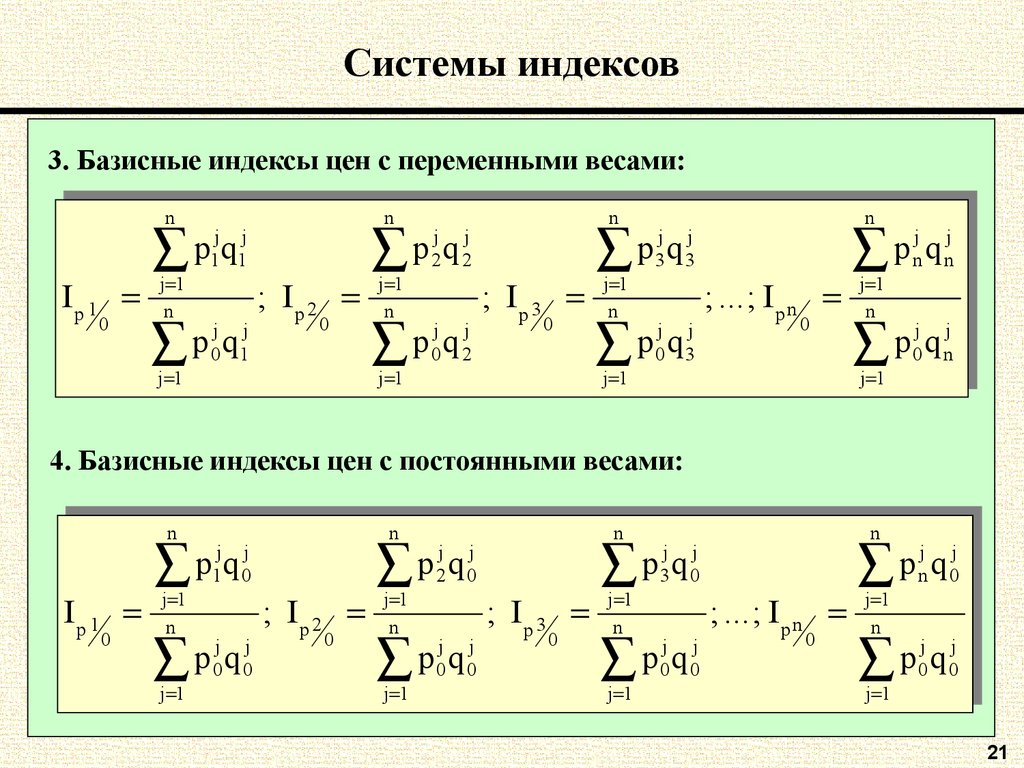
20. Системы индексов

1. Цепные индексы цен с переменными весами:
nn
IIpp110
0
j jqj j
p
p11q11
j j 11
nn
nn
j j qj j
p
p 22q 22
j 1
j 1
;; IIpp221 nn
j j qj j
p
p 00q11
1
j j 11
j jqj j
p
p11q 22
nn
j j qj j
p
p33q 33
j 1
j 1
;; IIpp33 2 nn
2
j j 11
j j qj j
p
p 22q 33
nn
...;;II p n
;;...
p n n -1
n -1
j j 11
j j qj j
p
p nnq nn
j j 11
nn
j j qj j
p
p nn-1-1q nn
j j 11
2. Цепные индексы цен с постоянными весами:
nn
IIpp110
0
ppqq
j j 11
nn
jj jj
11 00
j j qj j
p
p 00q 00
j j 11
nn
pp qq
j 1
j 1
;; IIpp221 nn
1
jj jj
22 00
j jqj j
p
p11q 00
j j 11
nn
pp qq
j 1
j 1
;; IIpp33 2 nn
2
jj jj
33 00
j j qj j
p
p 22q 00
j j 11
nn
;;......;;IIppnn n -1
n -1
j j qj j
p
p nnq 00
j j 11
nn
j j qj j
p
p nn-1-1q 00
j j 11
20

21. Системы индексов

3. Базисные индексы цен с переменными весами:
nn
IIpp110
0
j jqj j
p
p11q11
j j 11
nn
nn
j j qj j
p
p 22q 22
j 1
j 1
;; IIpp22 0 nn
j j qj j
p
p 00q11
0
j j 11
j j qj j
p
p 00q 22
nn
j j qj j
p
p33q 33
j 1
j 1
;; IIpp33 0 nn
0
j j 11
j j qj j
p
p 00q 33
nn
j j qj j
p
p nnq nn
j 1
...;;II p n j n1
;;...
n
pn 0
0
j j 11
j j qj j
p
p 00q nn
j j 11
4. Базисные индексы цен с постоянными весами:
nn
IIpp110
0
ppqq
j j 11
nn
jj jj
11 00
j j qj j
p
p 00q 00
j j 11
nn
pp qq
j 1
j 1
;; IIpp22 0 nn
0
jj jj
22 00
j j qj j
p
p 00q 00
j j 11
nn
pp qq
j 1
j 1
;; IIpp33 0 nn
0
jj jj
33 00
j j qj j
p
p00q 00
j j 11
nn
j j qj j
p
p nnq 00
j 1
...;;II p n j n1
;;...
n
pn 0
0
j j qj j
p
p 00q 00
j j 11
21

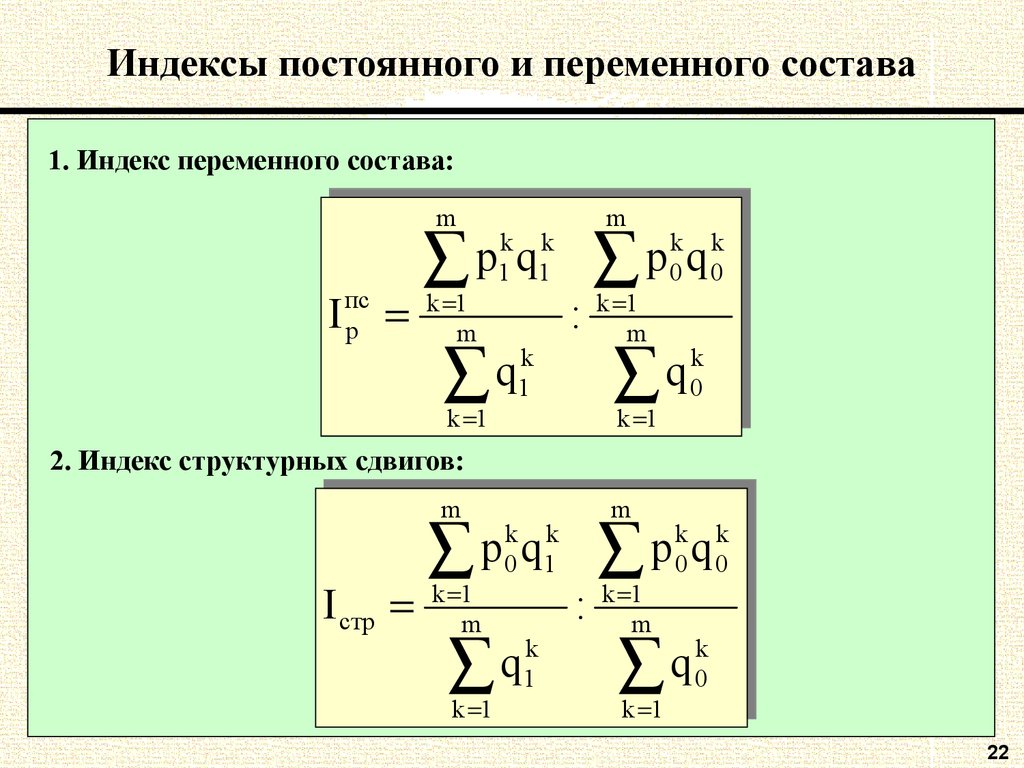
22. Индексы постоянного и переменного состава

1. Индекс переменного состава:
mm
kk qkk
p
p11q11
kk 11
I
I mm
пс
пс
pp
qq
kk 11
kk
11
mm
kk qkk
p
p00q 00
:: kk 11m
m
qq
kk 11
kk
00
2. Индекс структурных сдвигов:
mm
mm
pp qq
pp qq
kk 11
I
I стр
стр
mm
kk kk
00 11
qq
kk 11
kk
11
:: kk 11m
m
kk kk
00 00
qq
kk 11
kk
00
22

23. Индексы постоянного и переменного состава

3. Индекс цен фиксированного состава:
m
m
pp qq
kk 11
I
I mm
фс
фс
pp
kk kk
11 11
p
q
p
q
kk 11
kk kk
00 11
II IIстр
II
стр
пс
пс
pp
фс
фс
pp
23

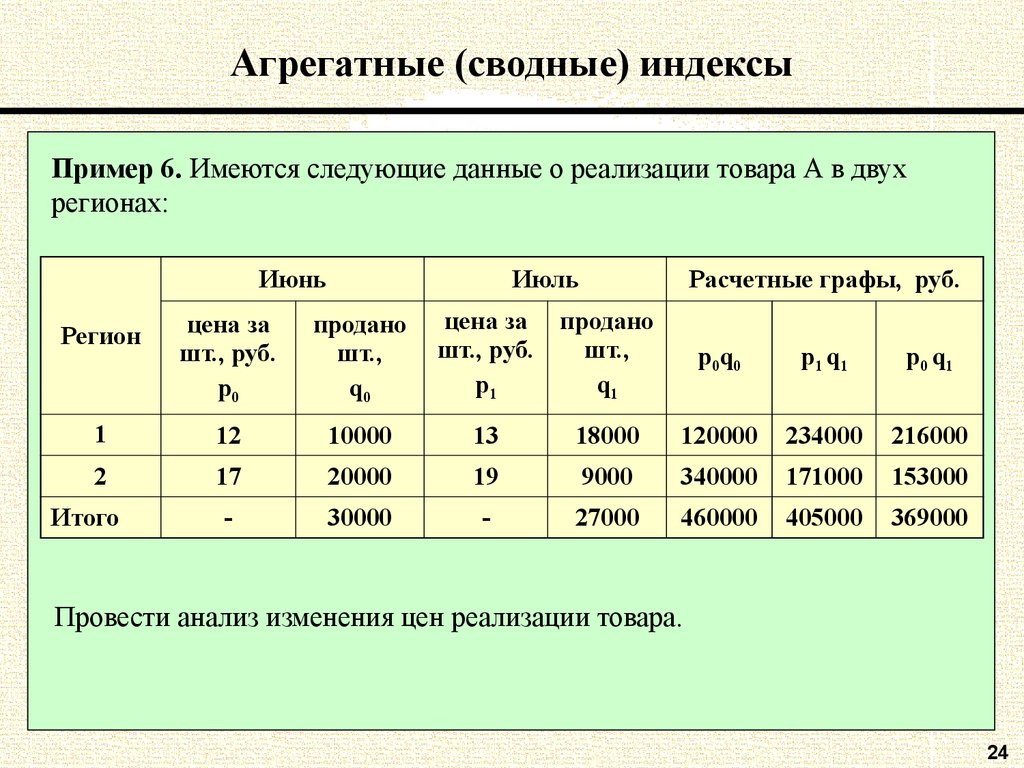
24. Агрегатные (сводные) индексы

Пример 6. Имеются следующие данные о реализации товара А в двух
регионах:
Июнь
Июль
Расчетные графы, руб.
Регион
цена за
шт., руб.
p0
продано
шт.,
q0
цена за
шт., руб.
p1
продано
шт.,
q1
p0q0
p1 q1
p0 q1
1
12
10000
13
18000
120000
234000
216000
2
17
20000
19
9000
340000
171000
153000
-
30000
-
27000
460000
405000
369000
Итого
Провести анализ изменения цен реализации товара.
24

25. Индексы постоянного и переменного состава

1. Индекс цен переменного состава:
m
I
пс
p
p q
k 1
m
m
k k
1 1
k
q
1
:
k k
p
0q0
k 1
m
k
q
0
k 1
405000 460000
:
15,00 : 15,33 0,978
27000 30000
k 1
2. Индекс структурных сдвигов:
m
I стр
p q
k 1
m
k
q
1
k 1
m
k k
0 1
:
k k
p
0q0
k 1
m
k
q
0
369000 460000
:
0,891 или 89,1%
27000 30000
k 1
25

26. Индексы постоянного и переменного состава

3. Индекс цен фиксированного состава:
m
I
фс
p
k k
p
1 q1
k 1
m
k k
p
0 q1
405000
1,098 или 109,8%
369000
k 1
I I I стр 1,098 0,891 0,978
пс
p
фс
p
26

27. Территориальные индексы

Территориальные индексы служат для сравнения показателей в
пространстве, т.е. по предприятиям, округам, городам, районам,
республикам, странам и пр.
Способы расчета территориальных индексов.
1. В качестве весов принимается сумма объемов проданных товаров по
двум регионам:
Q qa qb
Территориальный индекс цен:
m
I pb/a
k
p
bQ
k 1
m
k
p
aQ
k 1
27

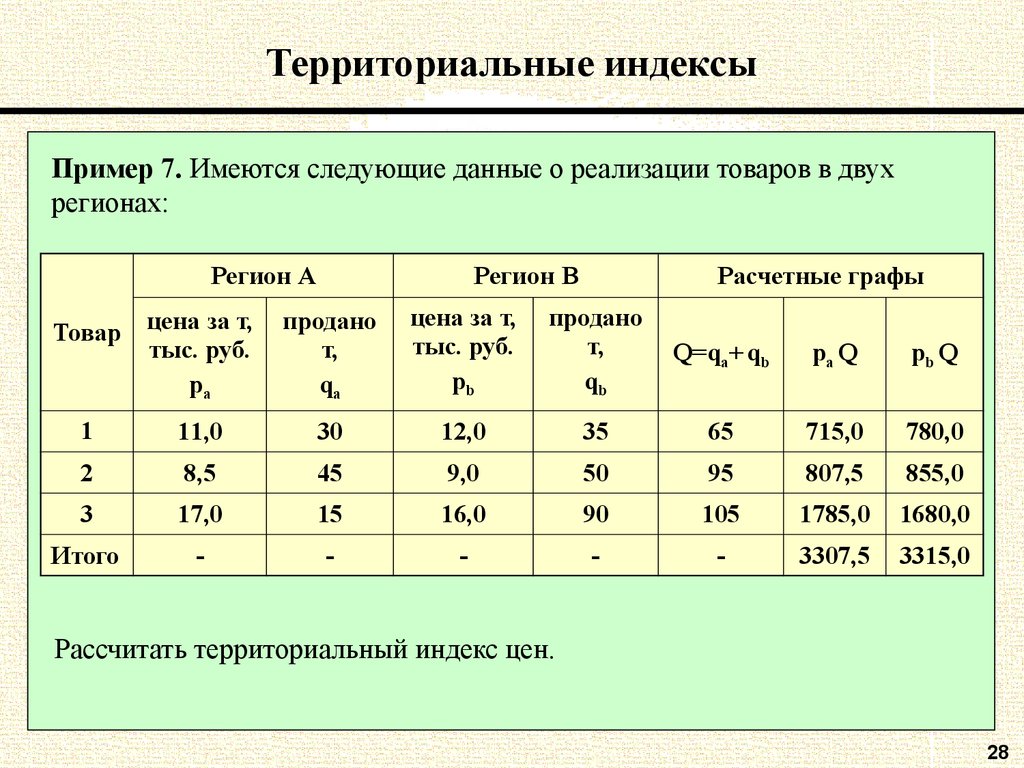
28. Территориальные индексы

Пример 7. Имеются следующие данные о реализации товаров в двух
регионах:
Регион А
Товар цена за т,
тыс. руб.
pа
Регион В
Расчетные графы
продано
т,
qa
цена за т,
тыс. руб.
pb
продано
т,
qb
Q=qa+ qb
pa Q
pb Q
1
11,0
30
12,0
35
65
715,0
780,0
2
8,5
45
9,0
50
95
807,5
855,0
3
17,0
15
16,0
90
105
1785,0
1680,0
Итого
-
-
-
-
-
3307,5
3315,0
Рассчитать территориальный индекс цен.
28

29. Территориальные индексы

Территориальный индекс цен:
m
I pb/a
k
p
bQ
k 1
m
k
p
aQ
3315,0
1,002 или 100,2%
3307,5
k 1
или
m
I pa/b
k
p
aQ
k 1
m
k
p
bQ
3307,5
0,998 или 99,8%
3315,0
k 1
29

30. Территориальные индексы

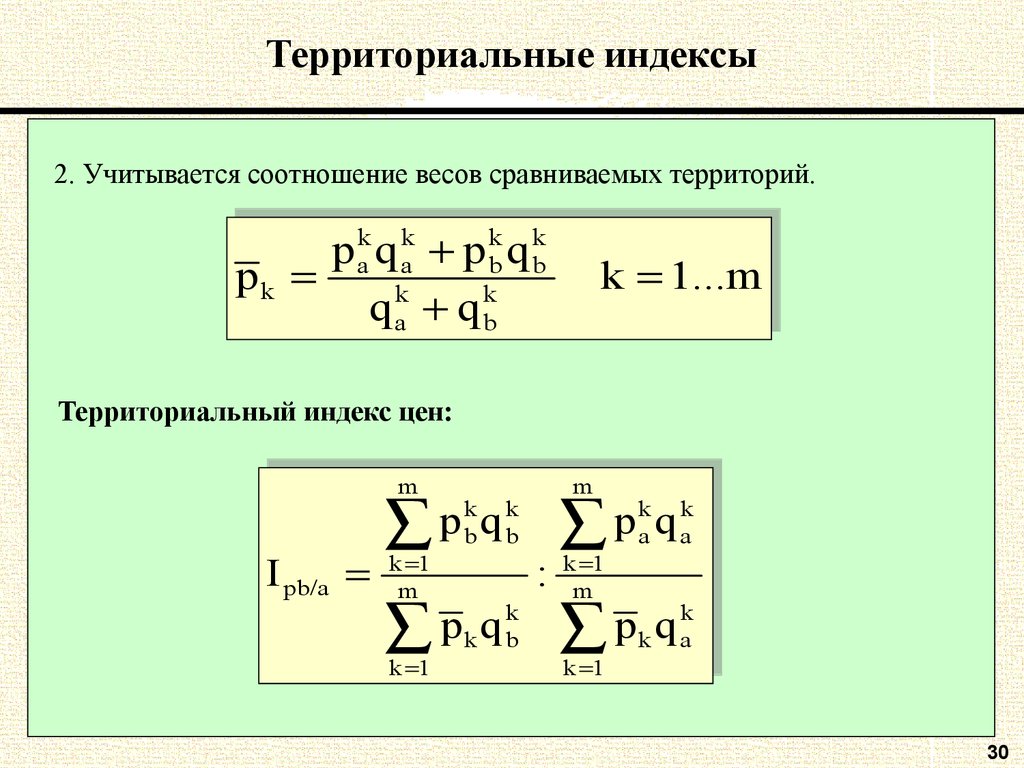
2. Учитывается соотношение весов сравниваемых территорий.
kk qkk pkk qkk
p
p aaq aa p bbq bb
p
p kk
kk qkk
q
q aa q bb
1...m
kk 1...m
Территориальный индекс цен:
m
m
kk qkk
p
p bbq bb
m
m
kk qkk
p
p aaq aa
kk 11
I
I pb/a
pb/a m
m
kk 11
:
: mm
kk 11
kk 11
kk
p
q
pkkq bb
kk
p
q
pkkq aa
30

31. Территориальные индексы

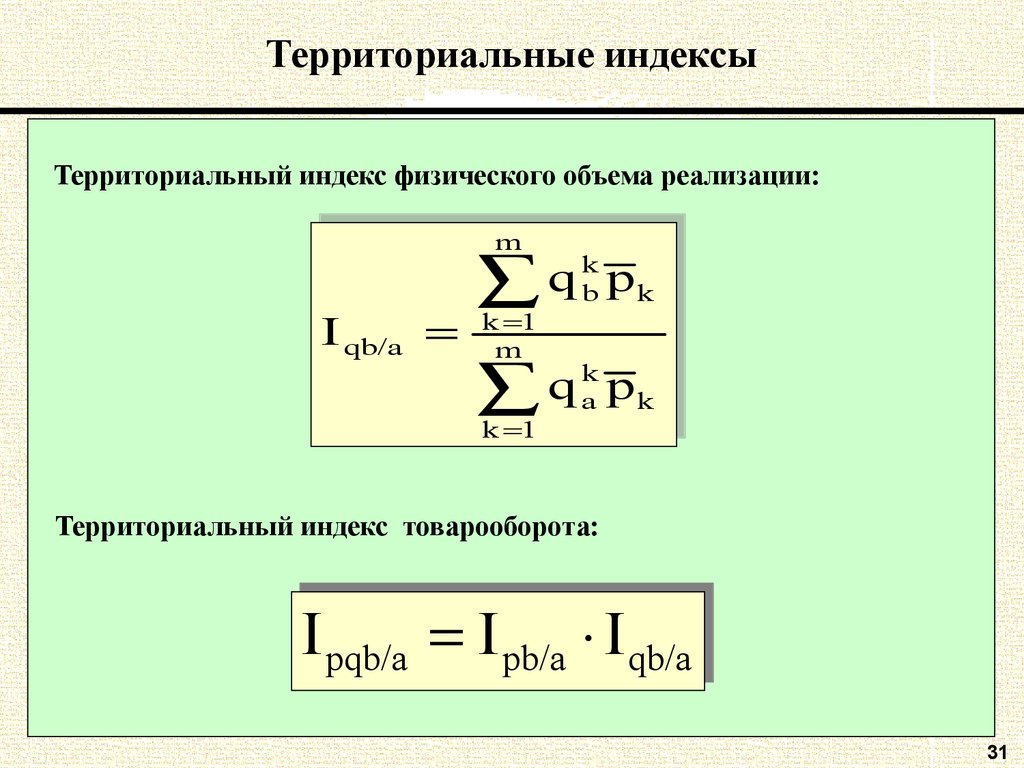
Территориальный индекс физического объема реализации:
m
m
IIqb/a
qb/a
kk p
q
q bbp kk
kk 11
m
m
kk p
q
q aap kk
kk 11
Территориальный индекс товарооборота:
IIpb/a
IIpqb/a
pqb/a
pb/a IIqb/a
qb/a
31

32. Территориальные индексы

Для примера 7:
p1a q1a p1b q1b 11,0 30 12,0 35
p1
11,54
1
1
qa qb
65
p a2 q a2 p 2b q 2b 8,5 45 9,0 50
p2
8,76
2
2
qa qb
95
p 3a q 3a p 3b q 3b 17,0 15 16,0 90
p3
16,14
3
3
qa qb
105
32

33. Территориальные индексы

Территориальный индекс цен:
I pb/a
12,0 35 9,0 50 16,0 90
11,0 30 8,5 45 17,0 15
:
11,54 35 8,76 50 16,14 90 11,54 30 8,76 45 16,14 15
1.022 или 102,2%
Территориальный индекс физического объема реализации:
I qb/a
35 11,54 50 8,76 90 16,14
2294,50
30 11,54 45 8,76 15 16,14
2193,00
1,046
или
104,6%
Территориальный индекс товарооборота:
I pqb/a I pb/a I qb/a 1,022 1,046 1,069 или 106,9%
33