Индексы. Группы индексов

1. Индексы

Индекс – относительный показатель,
характеризующий изменение
общественных явлений во времени, в
пространстве или по сравнению с
планом.
Индексируемая величина – значение
признака статистической совокупности,
изменение которой является объектом
изучения.

2. С помощью индексов решаются следующие задачи:

Определяются средние изменения сложных,
непосредственно неизмеримых совокупностей во
времени, т.е. индексы выступают как
относительные величины динамики, относительные
величины выполнения плана.
Определяются изменения показателей,
принадлежащих различным территориям, т.е.
строятся территориальные индексы.
Определяется роль отдельных факторов,
неразрывно связанных с результативным
фактором. Изучается роль и влияние факторов.

3. Группы индексов

1) Степени охвата элементов совокупности:
1.1. Индивидуальные – соотношение уровня
явлений по отдельному виду единиц
совокупности. Построение сводится к
сопоставлению двух величин,
характеризующих уровень изучаемого
явления во времени, в производстве, по
сравнению с планом.
1.2. Общие (сводные) – отражающие
изменение всех элементов сложного явления.
Под сложным явлением понимают такую
совокупность, отдельные элементы которой
непосредственно не подлежат
суммированию.

4.

2) Содержанию изучаемых объектов:
2.1. Индексы качественных показателей –
характеризующих свойство или качество
явления в расчете на единицу совокупности.
2.2. Индексы количественных (объемных)
показателей – характеризуют суммарный
объем (размер) того или иного явления.
3)Методам расчета общих индексов:
3.1. Агрегатные
3.2. Средние

5.

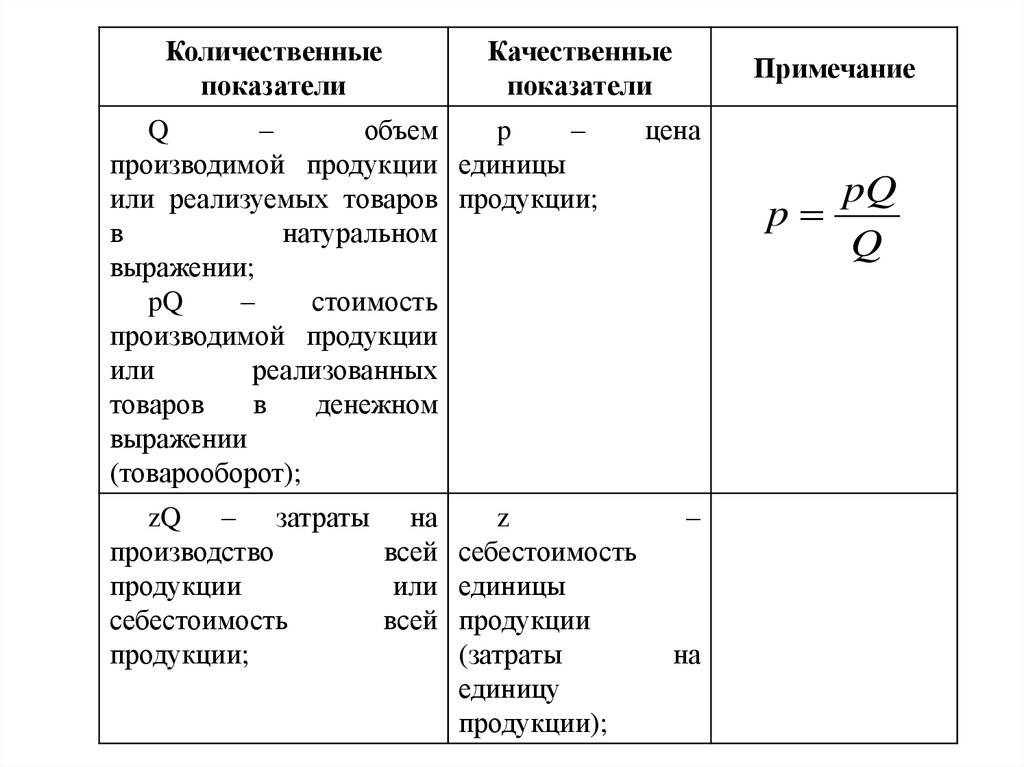
Количественные
показатели
Качественные
показатели
Q
–
объем
p
–
производимой продукции единицы
или реализуемых товаров продукции;
в
натуральном
выражении;
pQ
–
стоимость
производимой продукции
или
реализованных
товаров
в
денежном
выражении
(товарооборот);
zQ – затраты на
z
производство
всей себестоимость
продукции
или единицы
себестоимость
всей продукции
продукции;
(затраты
единицу
продукции);
Примечание
цена
pQ
p
Q
–
на

6.

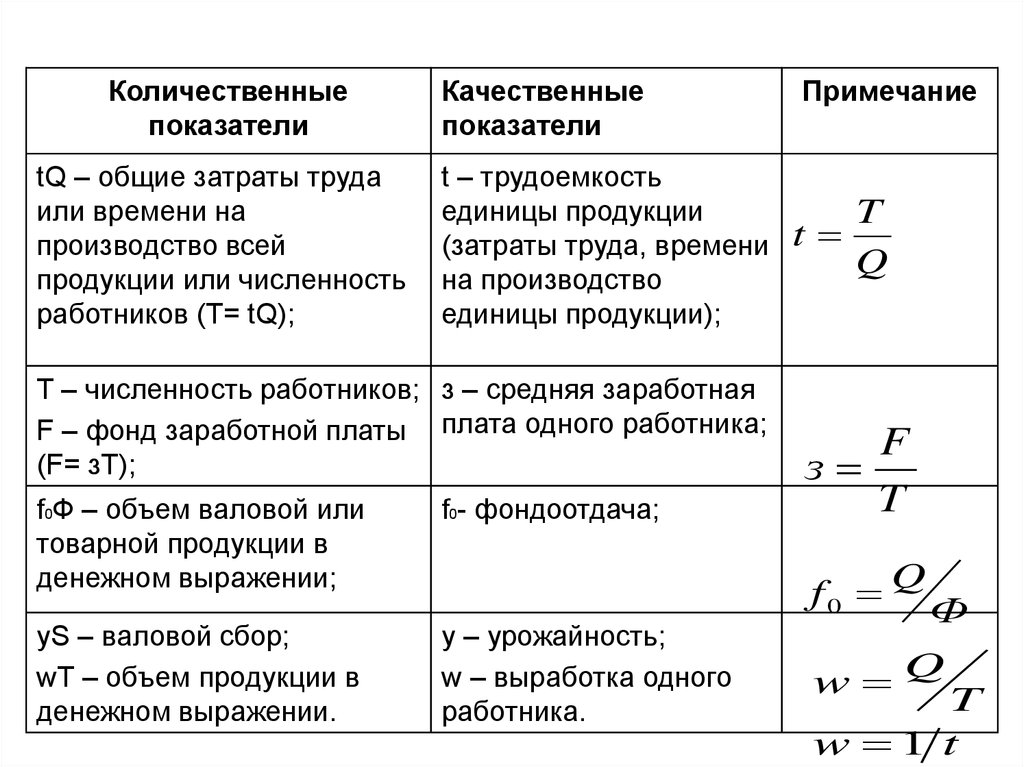
Количественные
показатели
tQ – общие затраты труда
или времени на
производство всей
продукции или численность
работников (Т= tQ);
Качественные
показатели
t – трудоемкость
единицы продукции
(затраты труда, времени
на производство
единицы продукции);
T – численность работников; з – средняя заработная
F – фонд заработной платы плата одного работника;
(F= зТ);
f0Ф – объем валовой или
товарной продукции в
денежном выражении;
f0- фондоотдача;
уS – валовой сбор;
wT – объем продукции в
денежном выражении.
у – урожайность;
w – выработка одного
работника.
Примечание
T
t
Q
F
з
T
f0 Q
Ф
w Q
T
w 1 t

7. Построение индивидуальных индексов.

Индивидуальные индексы обозначаются буквой i и
снабжаются подстрочным знаком индексируемого
показателя (например, iр – индивидуальный индекс
цен и т.д.), строятся как обычные относительные
величины:
отч 1
Овд
баз 0
1
пл
1
0
0
пл
Овплз
пл
пл
баз
0
отч 1
Оввпл
пл
пл
Овд Овплз Оввпл

8. Пример.

• iр =р1/р0*100=99%
Цена единицы продукции в отчетном периоде
по сравнению с базисным снизилась на 1%;
• iр плз = рпл/р0*100=97%
Планировалось снижение цены единицы
продукции на 3% или цена единицы
продукции в плановом периоде по
сравнению с базисным снизилась на 3%;

9. Пример.

• iр впл =р1/рпл*100=101%
Цена единицы продукции в отчетном периоде
увеличилась на 1% или план по цене
единицы продукции перевыполнили на 1%;
• it =t1/t0*100=102%
Трудоемкость единицы продукции в отчетном
периоде по сравнению с базисным
увеличилась на 2%;
• i1/t =t0/t1*100=102%
Выработка единицы продукции в отчетном
периоде по сравнению с базисным
увеличилась на 2%.

10.

На основе индексов можно определить абсолютные
изменения тех или иных показателей. Для этого нужно из
числителя индекса вычесть его знаменатель.
Iз = з1/з0*100 → з1 − з0= ± 1000
Заработная плата одного работника увеличилась (+) или
уменьшилась (-) на 1000 в отчетном периоде по
сравнению с базисным, либо абсолютное изменение
заработной платы работника в отчетном периоде по
сравнению с базисным составило 1000.
На основании индекса заработной платы планового
задания:
Зпл – Зо = +2500
Планировалось абсолютное увеличение заработной платы
одного работника на 2500.

11. Построение сводных индексов.

• Сводный индекс характеризует соотношение уровней
сложного явления, состоящего из нескольких различных видов,
не поддающихся непосредственному суммированию единиц.
• Сводные индексы, каждый из которых отражает соотношение
уровней отдельной группы единиц, называются групповыми.
• Общий – это сводный индекс, охватывающий все группы.
Сводные индексы разделяются в зависимости от метода расчёта. В
каждом индексе различают индексное число, т. е. результат
полученного соотношения, и индексное отношение,
показывающее методику расчета индекса.

12.

Сводные индексы
агрегатные
средние
Агрегатные индексы строятся на основании
сопоставления общих уровней явления, т. е.
это отношение суммы отчётных значений
индексированного признака, взвешенного на
соответствующее значение, к сумме базисных
значений признака.

13. Построение агрегатных индексов сопоставимых объемных показателей.

• Сводится к построению обычных относительных
величин.
F1
IF
F0
зТ
з Т
1 1
0
105%
0
• Вывод: Фонд заработной платы всех работников в
отчётном году по сравнению с базисным увеличился
на 5%.

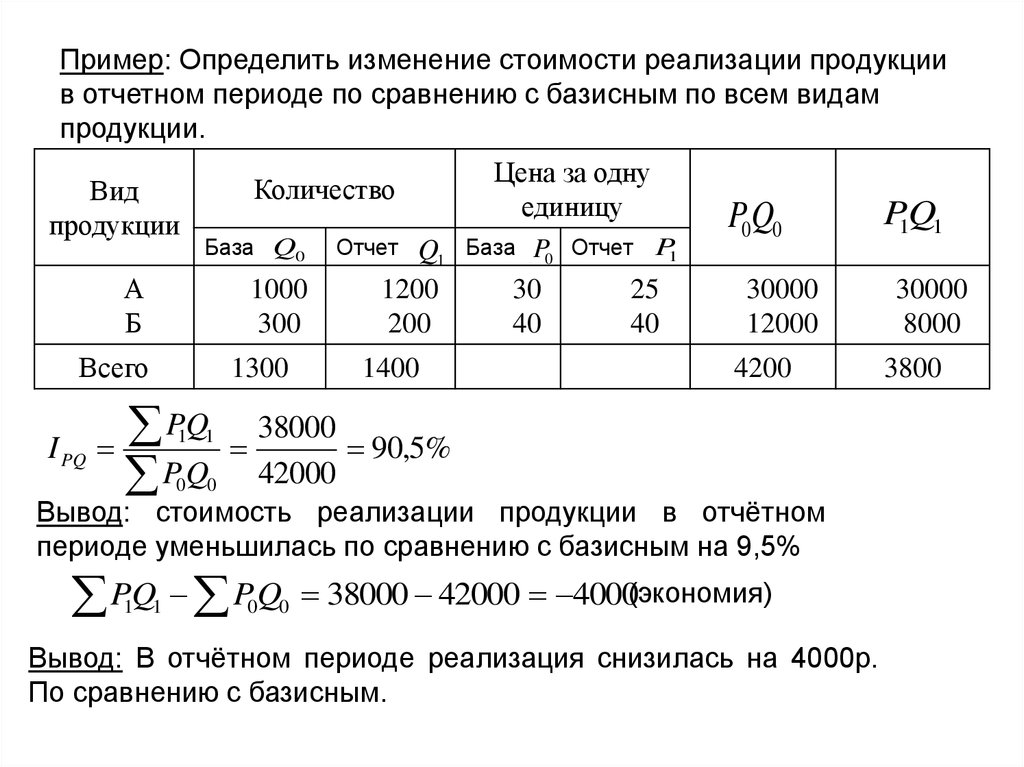
14. Пример: Определить изменение стоимости реализации продукции в отчетном периоде по сравнению с базисным по всем видам продукции.

Вид
продукции
Количество
База Q0
А
Б
1000
300
Всего
I PQ
1300
PQ
PQ
1 1
0
0
Отчет
Q1
1200
200
1400
Цена за одну
единицу
База P0 Отчет P1
30
40
25
40
P0Q0
30000
12000
4200
38000
90,5%
42000
Вывод: стоимость реализации продукции в отчётном
периоде уменьшилась по сравнению с базисным на 9,5%
PQ P Q
1 1
0
0
38000 42000 4000(экономия)
Вывод: В отчётном периоде реализация снизилась на 4000р.
По сравнению с базисным.
P1Q1
30000
8000
3800

15. Построение сводных индексов несоизмеримых объемных показателей и качественных показателей.

Построение несоизмеримых индексов и
называют индексами.
Построение этих индексов требует
использования особенностей индексного
метода.
1) Изменение изучаемого явления неразрывно
связано с другими явлениями. При этом
показатели-сомножители играют роль весов.
2) Устранение влияния весов осуществляется
путём их фиксирования в числителе и
знаменателе на одном и том же уровне.

16.

При построении агрегатных индексов качественных показателей
количественные фиксируются в индексе динамики на уровне
отчёта, в индексе планового задания на уровне плана.
p, z, t, з
Пример:
1) I
PQ
Ф, Q,
Т const
PQ
P Q
1
1
0
1
104%
• Вывод: Розничный товарооборот в отчётном году увеличился на
4% в результате изменения цены единицы продукции.
2)
P Q
I PQ
P Q
пл
пл
0
пл
98%
• Вывод: Запланировано снижение розничного товарооборота на
2% в результате изменения цены.

17.

Пример:
3)
I
zQ
z Q
1
пл
1
80%
1
Вывод: В отчётном году по сравнению с планом
себестоимость продукции была снижена на 20% в
результате снижения себестоимости единицы
продукции.
4)
t1Q1
It
99%
t 0 Q1
Вывод: Трудоёмкость снизилась на 1% в отчётном году
по сравнению с базой в результате изменения
трудоёмкости на единицу продукции.

18.

Пример:
5)
I1
t
t Q
t Q
0
1
1
1
102%
Вывод: Общая выработка в отчётном году по
сравнению с базой увеличилась на 2% в
результате изменения трудоёмкости на единицу
продукции.
Абсолютное изменение показателя можно
определить, если вычесть знаменатель из
числителя.
t0Q1 t1Q1 10 тыс. руб.
Вывод: Абсолютное изменение выпущенной
продукции увеличилось на 10 тыс. рублей в
результате изменения трудоёмкости.

19.

При построении агрегатных индексов объёмных показателей
возникает проблема взвешивания, которая решается путём
умножения объемных показателей на соответствующие
качественные.
При этом качественные показатели фиксируются в индексах
динамики на уровне базиса, в индексах выполнения плана на
уровне плана.
p, z, t,
з
Ф, Q, Т
const
Пример:
1) I PQ
PQ
P Q
0
1
0
0
105%
Вывод: Объём по всем видам продукции увеличился на 5% в
отчётном году по сравнению с базисным в результате изменения
объёма продукции по каждому виду.

20.

Агрегатные индексы объемных и качественных показателей
строятся для неоднородной совокупности, т. е. совокупно
представленной различными видами продукции и имеющими
разную потребительскую стоимость.
I PQ
PQ
P Q
1
1
пл
пл
P1Q1 Pпл Qпл 1 млн.
Абсолютное увеличение товарооборота в отчётном периоде по
сравнению с планом составило 1 млн. рублей в результате
изменения цены единицы продукции и объёма по каждому виду
продукции.
PQ
P Q
1
1
0
0
PQ
P Q
1
1
0
1
PQ
*
P Q
0
1
0
0

21. Преобразование агрегатного индекса в средний из индивидуальных

• Преобразование агрегатного индекса в средний осуществляется
путём подстановки в числитель или знаменатель вместо
индексируемого показателя показатель, полученный из
индивидуального индекса. Критерием правильности построения
среднего индекса является его равенство агрегатному индексу.
• Если подстановка производится в числитель агрегатного
индекса, то полученный индекс называют средним
арифметическим, если в знаменатель – средним
гармоническим.
I zQ
zQ
z Q
I zQ
1
1
0
1
z1
iz z1 iz z0
z0
izQ
z Q
z 0
0
1
1
средняя арифметическая
I zQ
z1
z0
iz
z1Q1
z1
i Q1
z
средняя гармоническая

22. Индексы средних величин.

Индексы средних величин строятся для однородных
совокупности, т. е. для совокупности предприятий,
выпускающих один вид продукции.
Поэтому индексы средних величин характеризуют
изменение средней цены по группам предприятий
(кроме цены может быть средняя себестоимость,
средняя трудоёмкость и т. д.).
Агрегатный индекс цены динамики характеризует
среднее изменение цены по всем видам продукции.
В индексах средних величин максимизируется
изменение средней цены по группам предприятий.
xвзв
x* f
f
P
P *Q
Q
Q
dQ
Q

23.

• Доля – это удельный вес продукции, производимой на каждом
предприятии, в общем объеме продукции на всех предприятиях.
IP
P1
P0
PQ
Q
1
PQ
Q
1
0
0
P dQ
P dQ
0
1
0
1
0
0
• Правила построения индексов распространяются и на
индексы средних величин.
I P фикс .состав а
PQ
Q
1
1
1
PQ
Q
0
1
1
P dQ
P dQ
1
0
1
1
• Полученный индекс называется индексом средней цены
фиксированного состава.
• Средний индекс фиксированного состава характеризует
изменение средней величины показателя по совокупности
предприятий в результате изменения качественного показателя на
каждом предприятии.

24.

• Полученный индекс – индекс средней величины
структурных сдвигов. Он характеризует изменение средней
величины показателя по группам предприятий в общем объёме
выпущенной продукции.
I P стр.сдвигов
P Q P Q
Q
Q
0
1
0
1
0
0
P dQ
P dQ
0
1
0
0
• Полученный индекс – индекс переменного состава.
I P перем.состава
PQ
Q
1
1
1
PQ
Q
0
0
0
I Рперем.сост I Pф.с. * I Рстр.сдв.
P dQ
P dQ
1
0
1
0

25.

• Пример:
I z п .с .
z dQ
z dQ
1
1
0
0
98%
• Вывод: Средняя себестоимость по группам предприятий в
отчётном году по сравнению с предыдущим годом снизилась на
2% за счёт изменения себестоимости единицы продукции на
каждом предприятии и доли продукции, произведённой на
каждом предприятии в общем объёме выпущенной продукции.
• Пример:
z z1dQ1 z0dQ0 10 тыс. рублей
• Вывод: Абсолютная экономия от снижения себестоимости по
группам предприятий составила 10 тыс. рублей в результате
изменения себестоимости единицы продукции на каждом
предприятии и доли продукции, произведённой на каждом
предприятии в общем объёме выпущенной продукции.

26.

• Пример:
I z .ф.с.
z
z
1
dQ1
0
dQ1
101%
• Вывод: Средняя себестоимость по группам предприятий в
отчётном году по сравнению с предыдущим годом увеличилась
на 1% в результате изменения себестоимости продукции на
каждом предприятии.
• Пример:
z z1dQ1 z0dQ1 3 тыс. рублей
• Вывод: Абсолютный перерасход себестоимости по группам
предприятий составил 3 тыс. рублей в результате изменения
себестоимости единицы продукции на каждом предприятии.

27.

• Пример:
I z .стр.сдв.
z dQ
z dQ
0
1
0
0
95%
• Вывод: Средняя себестоимость по группам
предприятий в отчётном году по сравнению с
предыдущим годом снизилась на 5% в результате
изменения доли выпущенной продукции на каждом
предприятии в общем объёме выпущенной
продукции.

28. Выявление влияния факторов с помощью индексного метода.

Фиксирование фактора на том или ином уровне для устранения его
влияния на результативный фактор зависит от цели анализа и
выводов, которые хотят получить.
Теоретически возможно 3 случая:
1. Независимо от последовательности изучения влияния
факторов фиксированные факторы берутся на уровне
базисного периода.
згод зчас * d * Д
Изменение среднегодовой заработной платы отчётного периода по
сравнению с базисным периодом в результате изменения
часовой заработной платы составило:
зч1
з * d * Д0
ч1 0
зч 0
зч 0 * d 0 * Д 0

29.

2.
Независимо от последовательности изучения
влияния отдельных факторов неизменные факторы
фиксируются на уровне отчётного периода.
зч1
зч1 * d1 * Д 1
зч 0 зч 0 * d1 * Д 0
Первые два случая – это метод изолированного
изучения влияния факторов. Т. к. все факторы
являются взаимосвязанными, правильно
применять третий случай.

30.

3. Метод цепных подстановок. При этом методе выявление
влияния факторов производится с учётом качественных и
количественных показателей.
На первом месте модели следует ставить качественные
показатели. Увеличение цепи факторов на один фактор
каждый раз должно приводить к показателю, имеющему
реальный экономический смысл.
зч * d зд
зч * d * Д з год
Зч
зч * d * Д * Т ФОТ
Згод

31. Четырёхфакторная модель

• Можно изучить влияние каждого фактора:
IФОТ
I ФОТ
I ФОТ
I ФОТ
з
з
ч1
* d1 * Д1 * Т1
ч0
* d1 * Д1 * Т1
з
з
ч0
* d1 * Д 1 * Т 1
ч0
* d 0 * Д1 * Т1
з
з
з
з
ч0
* d 0 * Д1 * Т1
ч0
* d 0 * Д 0 * Т1
ч0
* d 0 * Д 0 * Т1
ч0
* d0 * Д 0 *Т 0

32.

Индексные системы могут применяться и для определения в
абсолютном выражении изменения сложного явления за счёт
влияния отдельных факторов.
Расчёты, связанные с определением изменения результативного
показателя, называют разложением абсолютного прироста
по факторам.
a0b1c1d1
a0зb0 c1d1
–а
d
–b
Д
–с
Т
a1b1–c1d a0b0c0
(a1 a0 )b1c1 a0 (b1 b0 )c1 a0b0 c1 c0

33.

Индексы так же, как и относительные величины, могут быть
базисные, могут быть цепные.
• Индивидуальные индексы просты по построению:
Базисные:
Цепные:
i P1 / 0
i P1 / 0
P1
P0
P1
P0
i P2 / 0
P2
0
i P2 / 1
P2
P1

34.

Рассмотрим построение базисных и цепных индексов на примере
агрегатных индексов цен и физического объёма продукции.
1. Базисные индексы:
I P1/ 0
PQ
PQ
1
1
0
1
I P2 / 0
PQ
P Q
2
2
0
2
Индекс цен с переменным составом называется индексом Паше.
I P1/ 0
PQ
P Q
1
0
0
0
2. Цепные индексы:
I P2 / 0
PQ
PQ
2
2
1
1
- Паше
I P2 / 0
PQ
P Q
I P2 / 0
2
0
0
0
- индекс Ласпейреса
PQ
PQ
2
1
1
1
- Ласпейреса

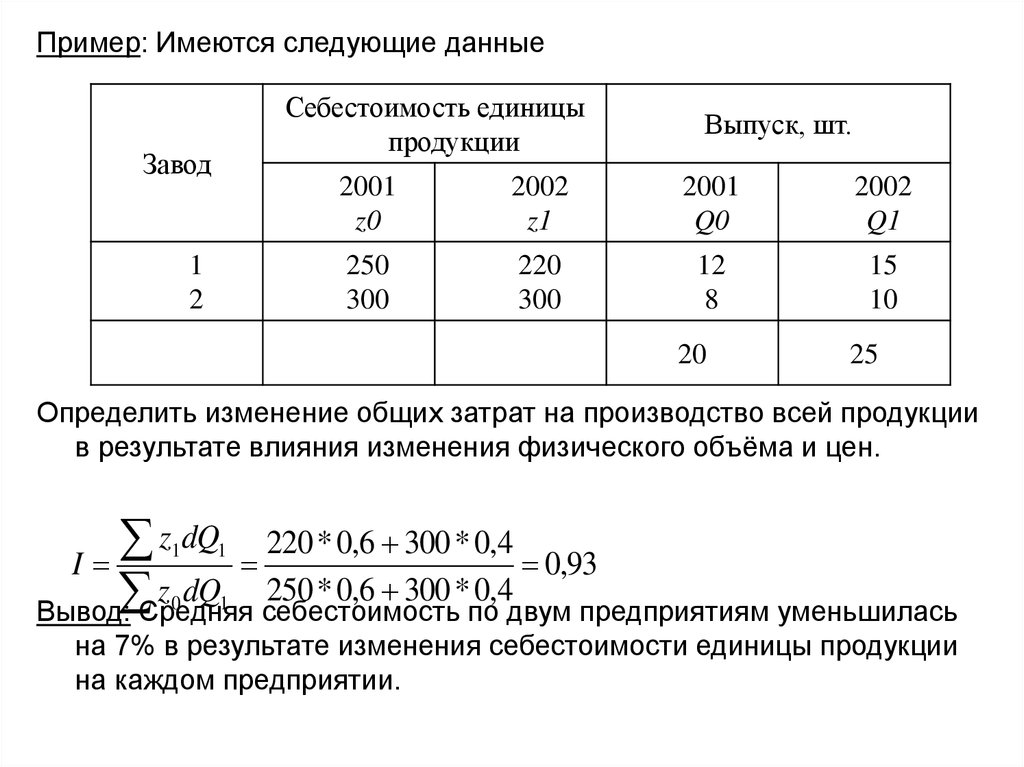
35.

Пример: Имеются следующие данные
Себестоимость единицы
продукции
Завод
1
2
Выпуск, шт.
2001
z0
2002
z1
2001
Q0
2002
Q1
250
300
220
300
12
8
15
10
20
25
Определить изменение общих затрат на производство всей продукции
в результате влияния изменения физического объёма и цен.
z dQ 220 * 0,6 300 * 0,4
I
0,93
z dQ 250 * 0,6 300 * 0,4
Вывод: Средняя себестоимость по двум предприятиям уменьшилась
1
1
0
1
на 7% в результате изменения себестоимости единицы продукции
на каждом предприятии.

36.

z dQ
I
z dQ
0
1
0
0
250 * 0,6 300 * 0,4
1
300 * 0,4 250 * 0,6
• Вывод: Средняя себестоимость по двум предприятиям осталась
без изменения в результате изменения доли выпускаемой
продукции на каждом предприятии в общем объёме.
z dQ
I
z dQ
1
1
0
0
220 * 0,6 300 * 0,4
0,93
300 * 0,4 250 * 0,6
• Вывод: Средняя себестоимость по двум предприятиям
уменьшилась на 7% в результате изменения себестоимости
единицы продукции на каждом предприятии и в результате
изменения доли выпускаемой продукции н каждом предприятии
в общем объёме.