Similar presentations:
Статика. «Дайте мне точку опоры, и я подниму Землю!»
1. СТАТИКА
«Дайте мне точку опоры, и я подниму Землю!» Эти словаприписывают Архимеду, уверовавшему во всемогущество
рычага. Даже если бы нашлась точка опоры, то, чтобы
сместить планету хотя бы на один сантиметр, руке
Архимеда пришлось бы проделать путь в 300 000 000 раз
больший, чем диаметр орбиты Земли!!!
2.
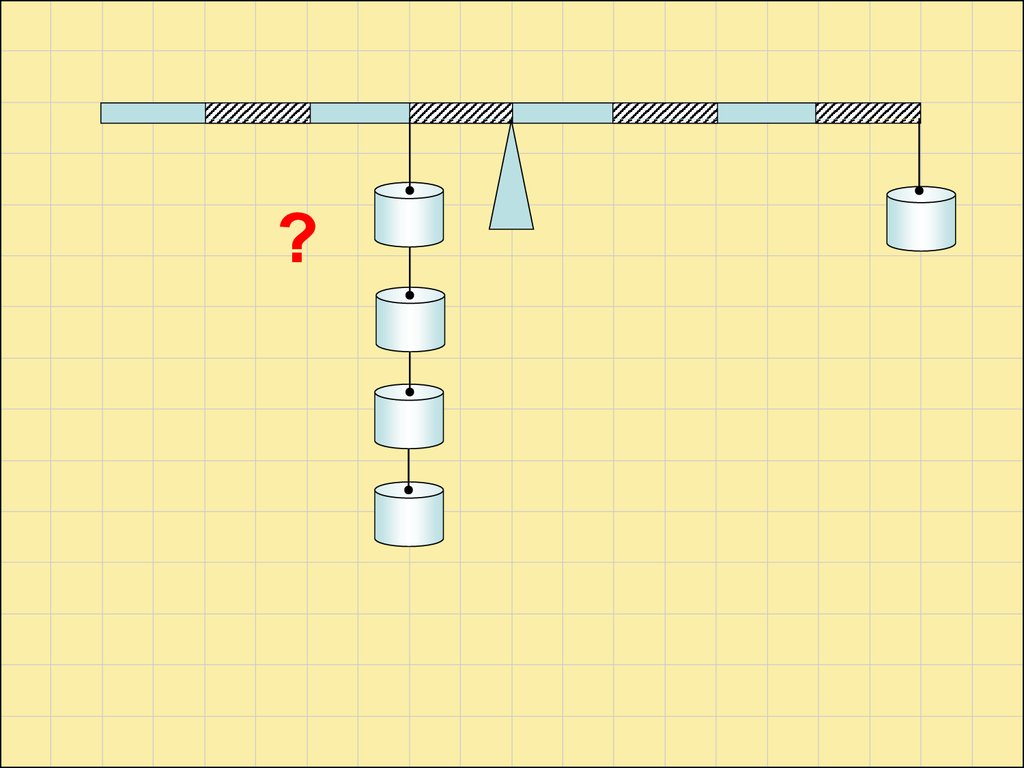
?3.
?4.
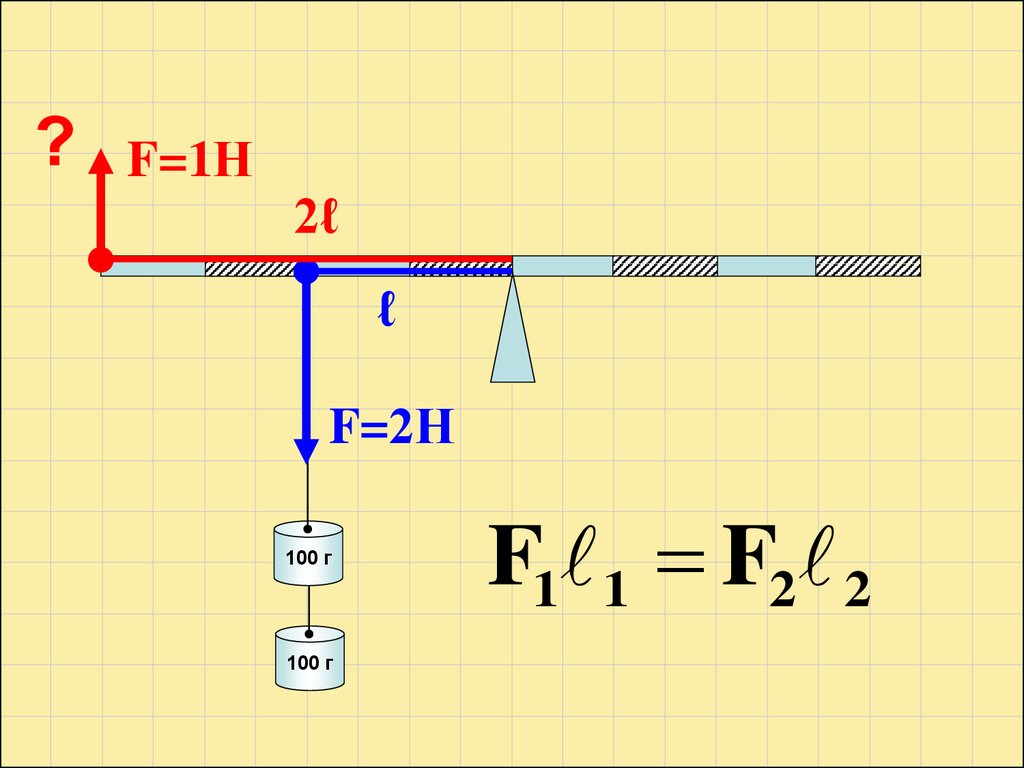
?F=1Н
2ℓ
ℓ
F=2Н
100 г
100 г
F1 1 F2 2
5.
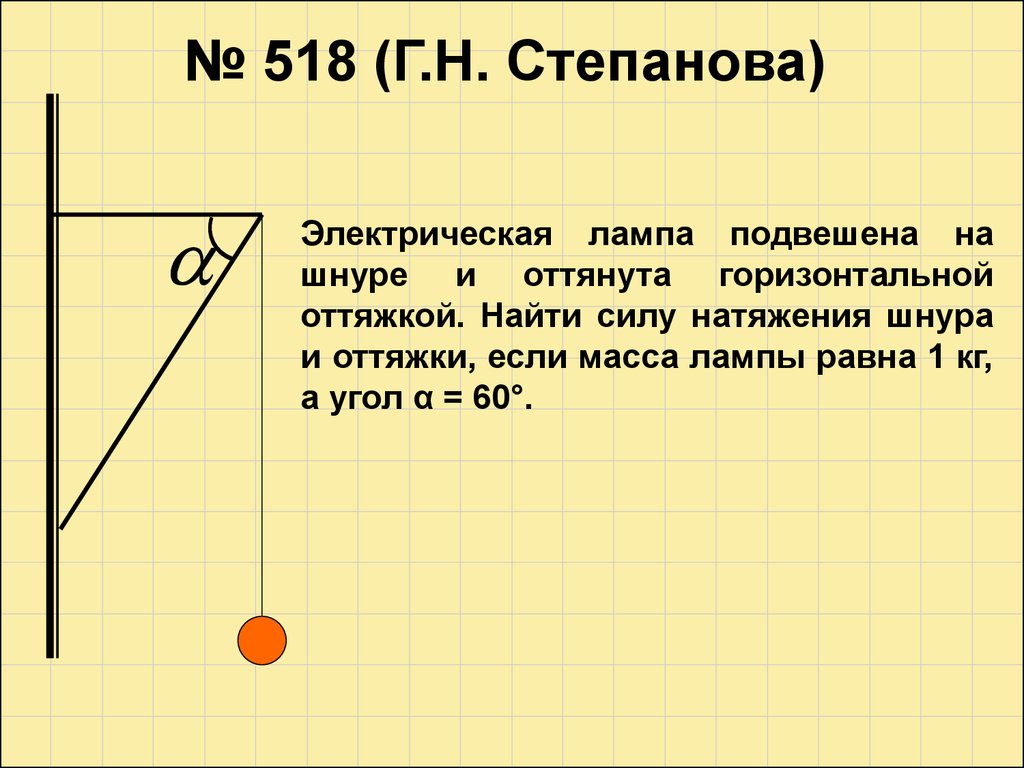
№ 518 (Г.Н. Степанова)Электрическая лампа подвешена на
шнуре и оттянута горизонтальной
оттяжкой. Найти силу натяжения шнура
и оттяжки, если масса лампы равна 1 кг,
а угол α = 60°.
6.
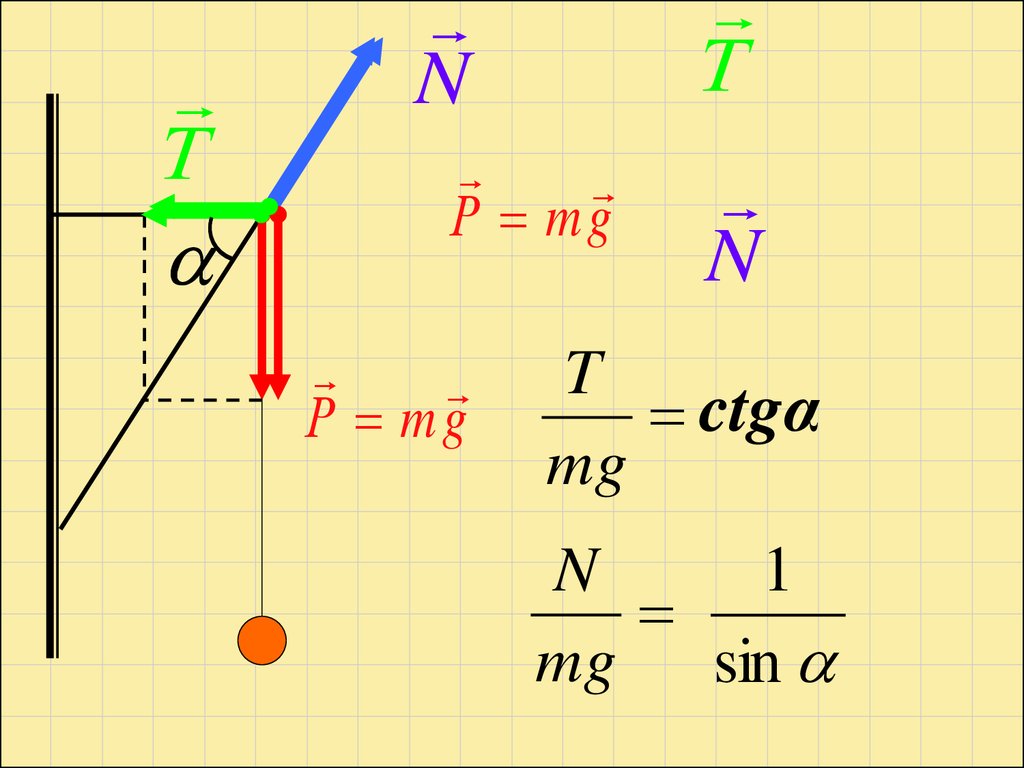
ТТ
N
Р mg
Р mg
N
T
ctgα
mg
N
1
mg sin
7.
ВА
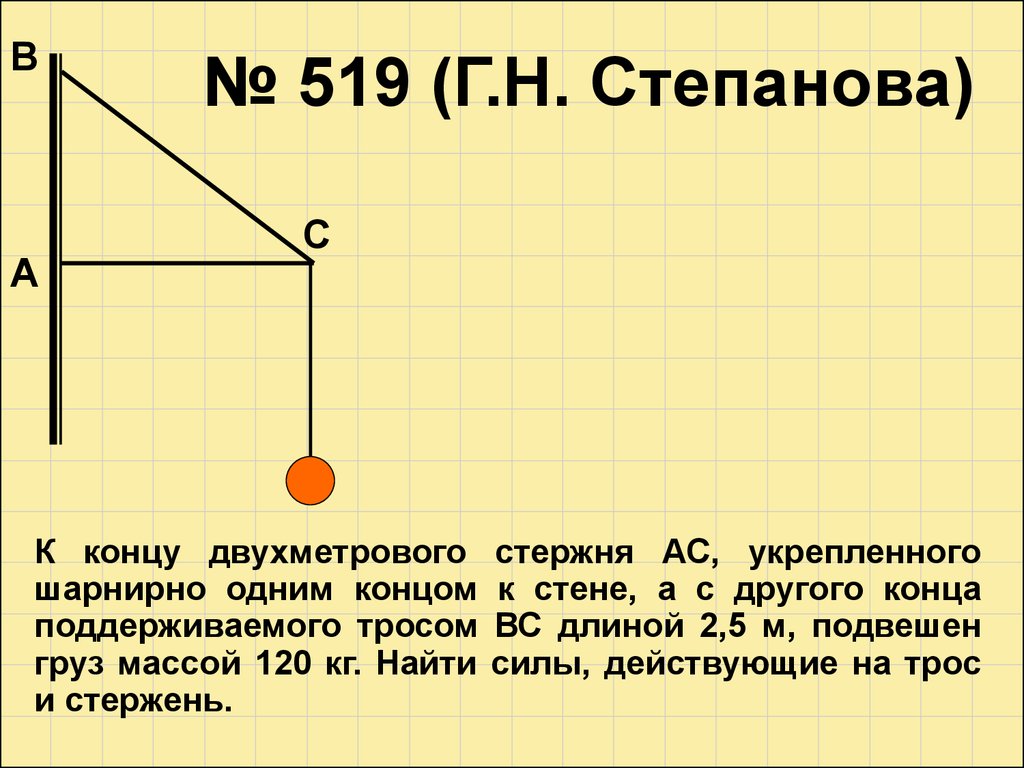
№ 519 (Г.Н. Степанова)
С
К концу двухметрового
шарнирно одним концом
поддерживаемого тросом
груз массой 120 кг. Найти
и стержень.
стержня АС, укрепленного
к стене, а с другого конца
ВС длиной 2,5 м, подвешен
силы, действующие на трос
8.
ТВ
А
Дано:
АС=2м=4/2 м
ВС=2,5м=5/2 м
m=120 кг
N-?
Т-?
Решение:
N
1) АВ=3/2 м
N
4
С
mg 3
4
N mg 1600 H
3
Р mg
3)
T
5
mg 3
2)
5
T m g 2000 H
3
9.
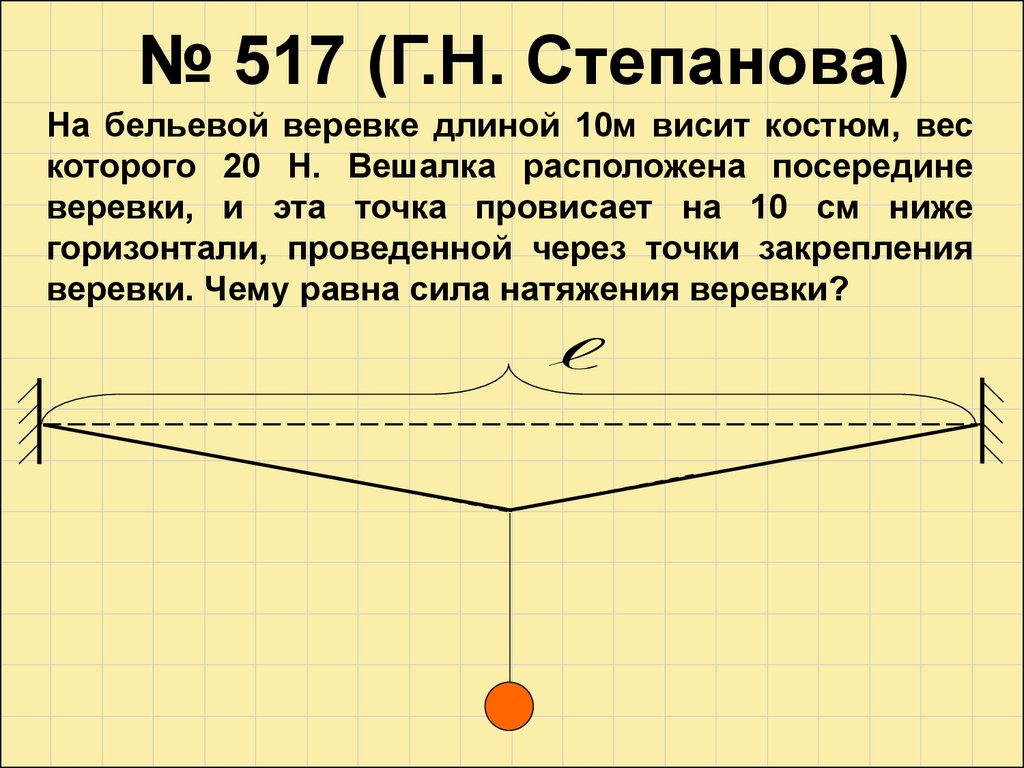
№ 517 (Г.Н. Степанова)На бельевой веревке длиной 10м висит костюм, вес
которого 20 Н. Вешалка расположена посередине
веревки, и эта точка провисает на 10 см ниже
горизонтали, проведенной через точки закрепления
веревки. Чему равна сила натяжения веревки?
10.
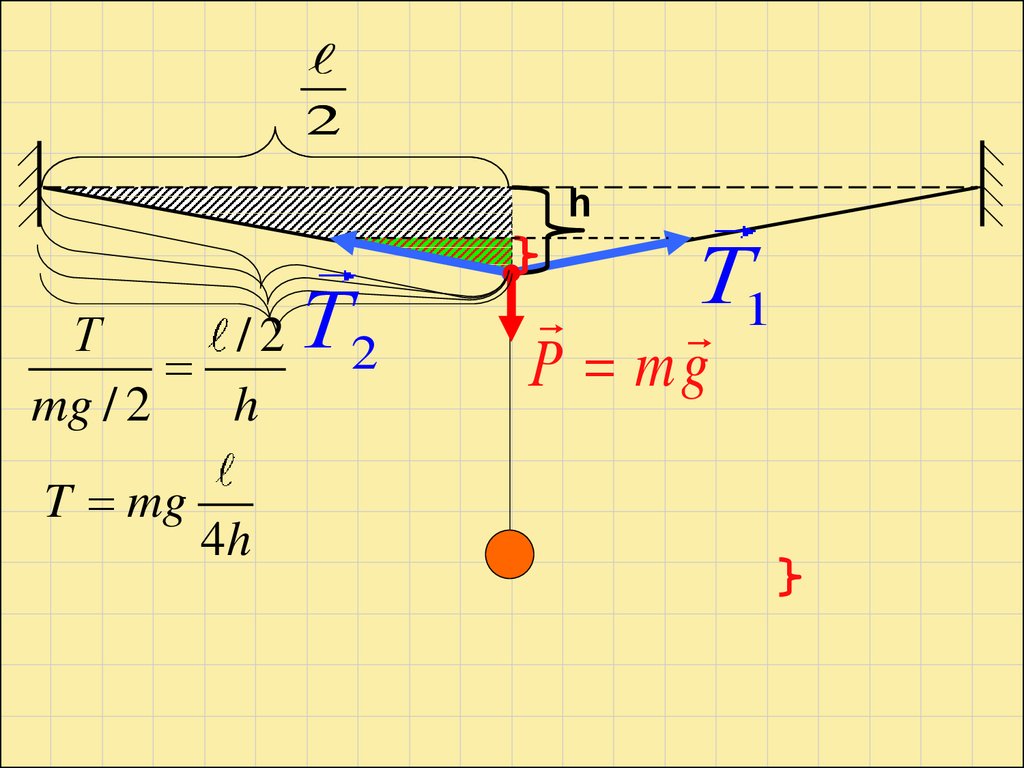
2h
Т
/2
mg / 2
h
T mg
4h
Т2
Т
1
Р mg
11.
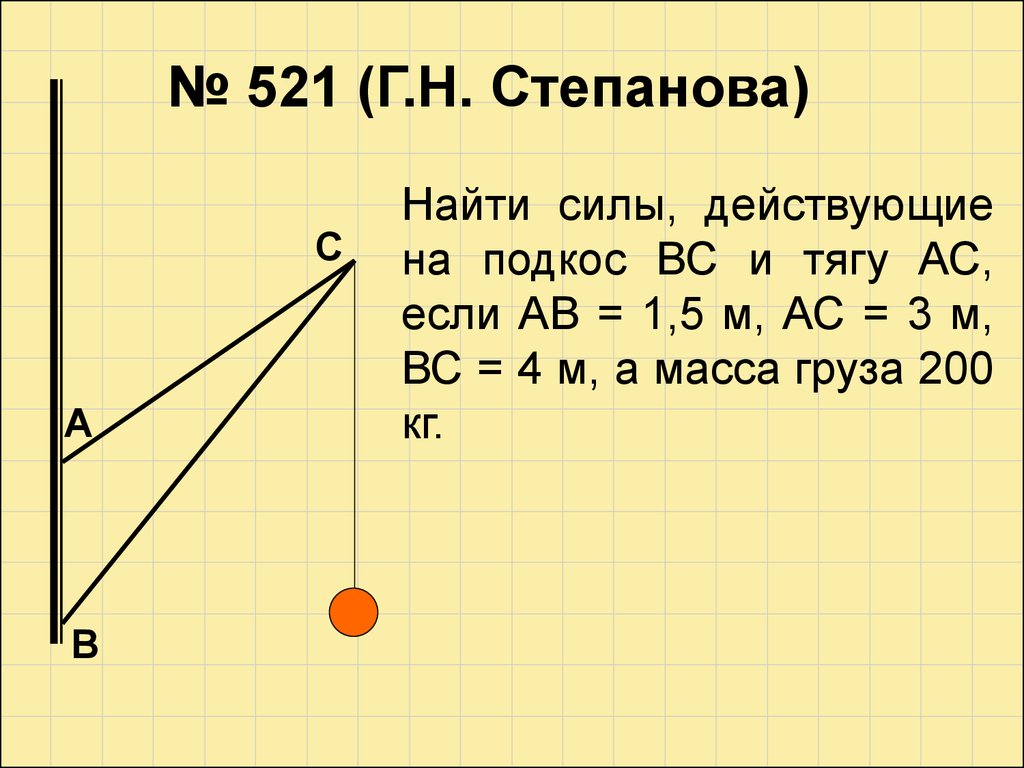
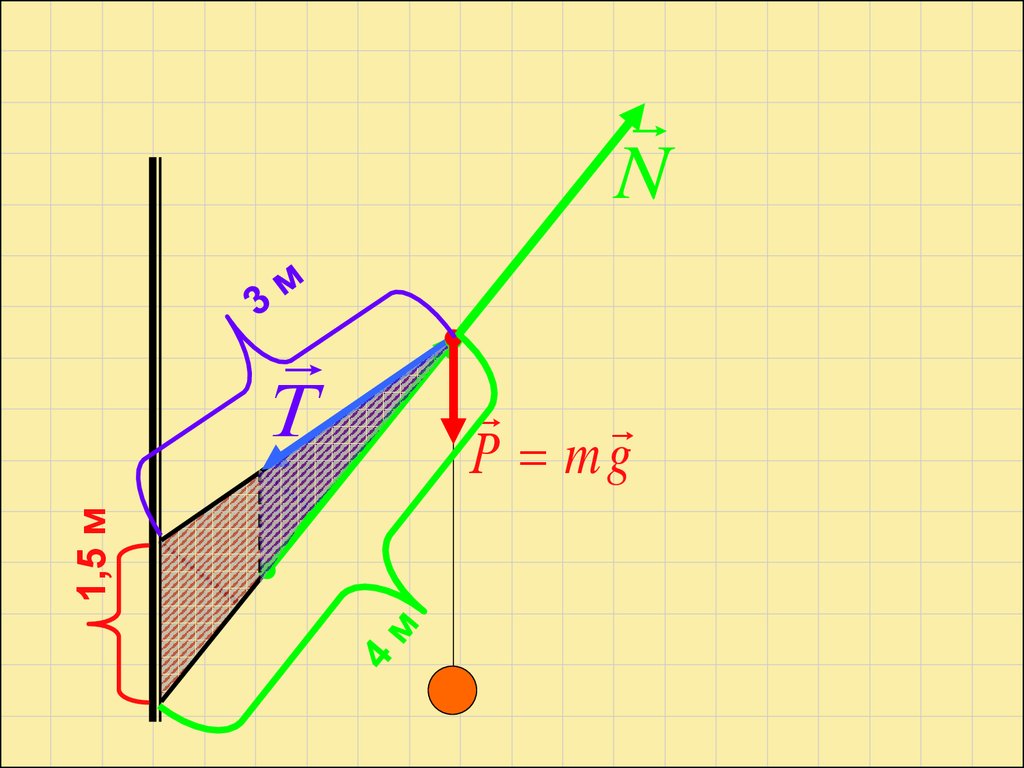
№ 521 (Г.Н. Степанова)С
А
В
Найти силы, действующие
на подкос ВС и тягу АС,
если АВ = 1,5 м, АС = 3 м,
ВС = 4 м, а масса груза 200
кг.
12.
N1,5 м
Т
Р mg
13.
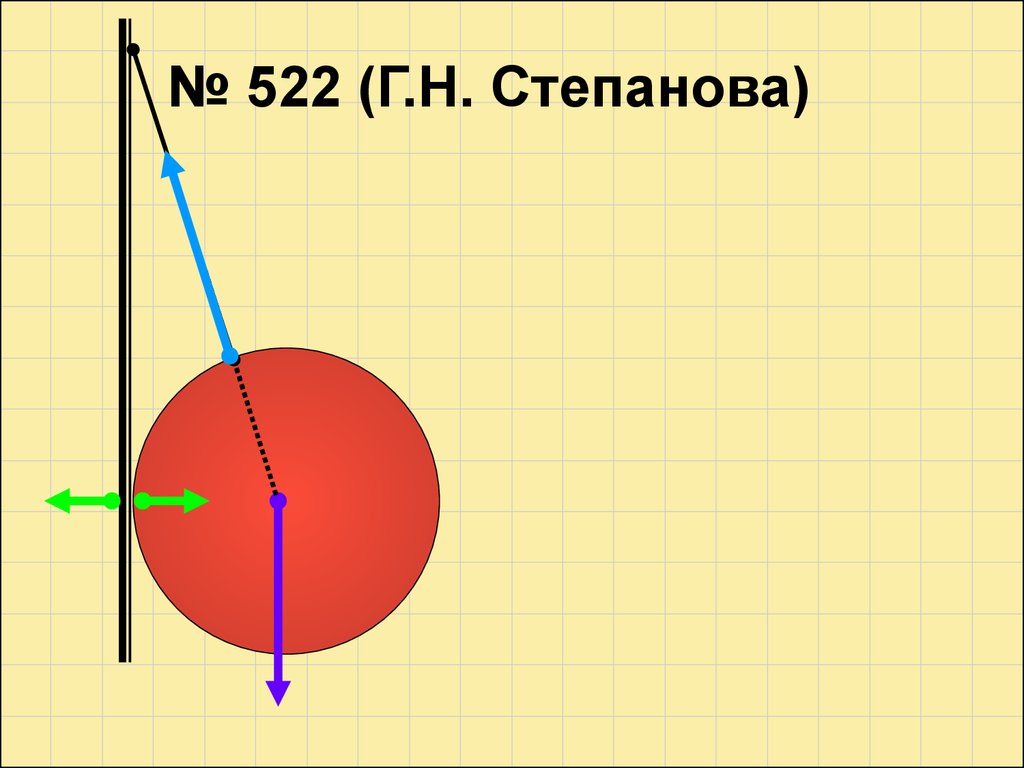
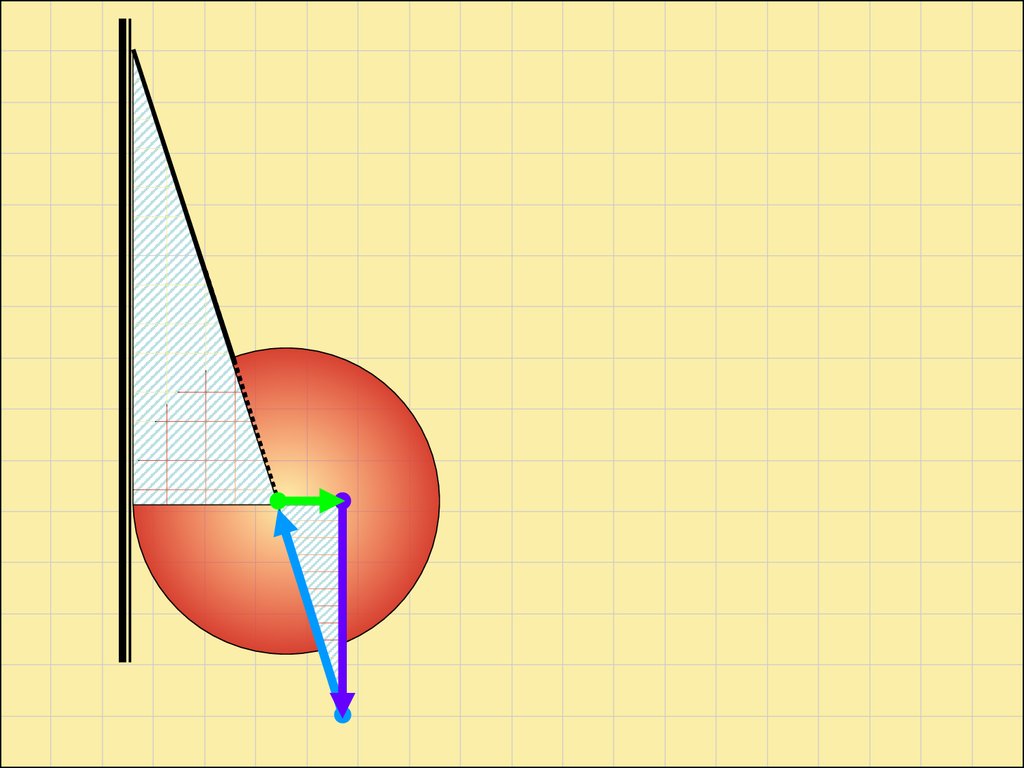
№ 522 (Г.Н. Степанова)14.
15.
Бревно длиной 12 м можно уравновесить в горизонтальномположении на подставке, отстоящей на 3 м от ее толстого конца.
Если же подставка находится в 6 м от толстого конца и на тонкий
конец сядет рабочий массой 60 кг, бревно снова будет в равновесии.
Определить массу бревна.
N1
2
0
4
8
6
12
X, м
∑Мiо=0:
3
О
P1 =m1g
+
10
mg
N
6
9
-
m g 6 mg 3
1
mg
m 2m1 120 кг
16.
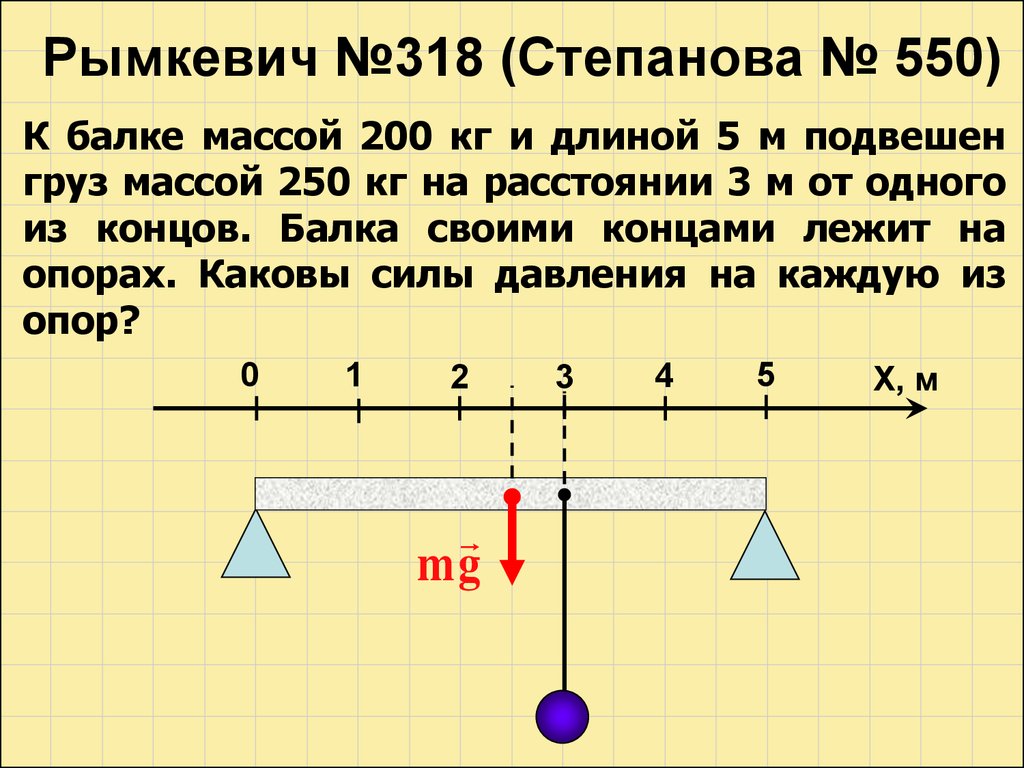
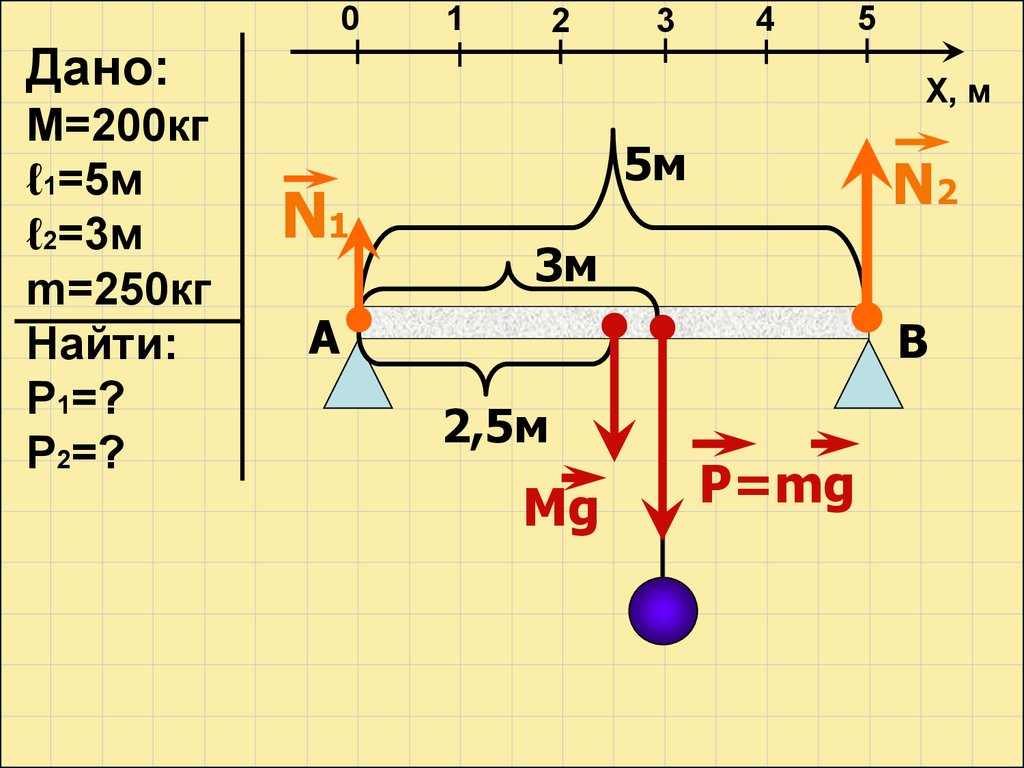
Рымкевич №318 (Степанова № 550)К балке массой 200 кг и длиной 5 м подвешен
груз массой 250 кг на расстоянии 3 м от одного
из концов. Балка своими концами лежит на
опорах. Каковы силы давления на каждую из
опор?
0
1
2
mg
3
4
5
X, м
17.
01
2
Дано:
M=200кг
ℓ1=5м
ℓ2=3м
m=250кг
Найти:
Р1=?
Р2=?
3
4
5
X, м
N1
5м
N2
3м
A
B
2,5м
Mg
P=mg
18.
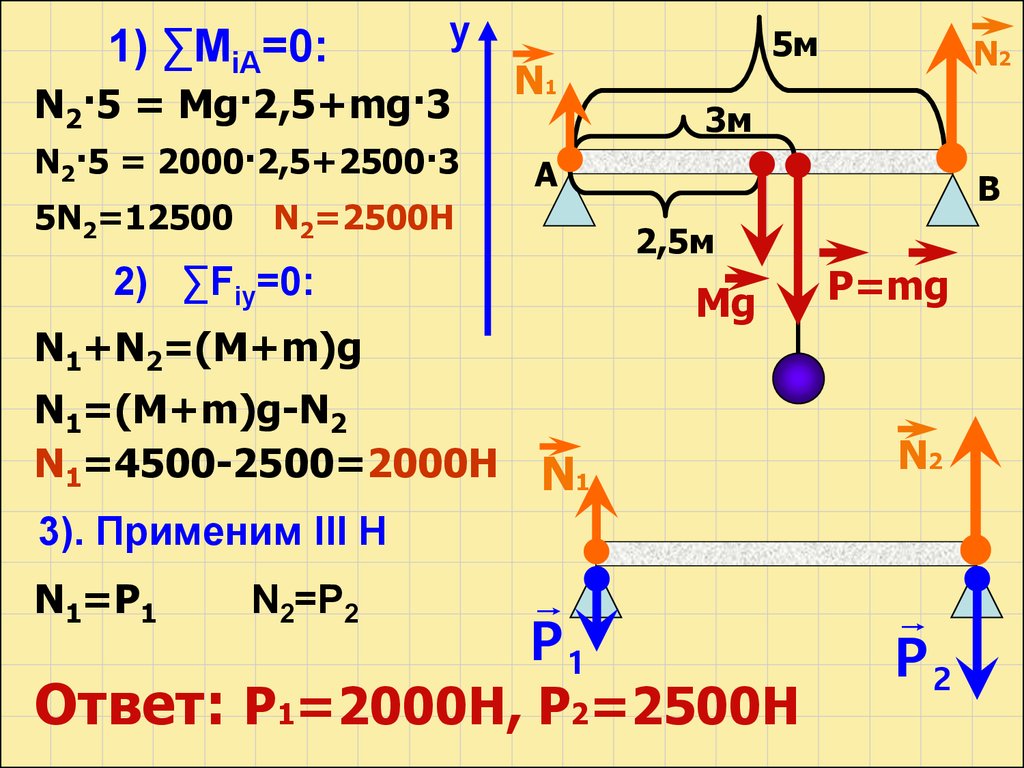
1) ∑МiA=0:у
N2·5 = Mg·2,5+mg·3
N2·5 = 2000·2,5+2500·3
5N2=12500
N1
N2
3м
A
N2=2500H
B
2,5м
2) ∑Fiy=0:
Mg
N1+N2=(M+m)g
N1=(M+m)g-N2
N1=4500-2500=2000H
5м
P=mg
N1
N2
Р1
Р2
3). Применим III H
N1=P1
N2=P2
Ответ: P1=2000H, P2=2500H
19.
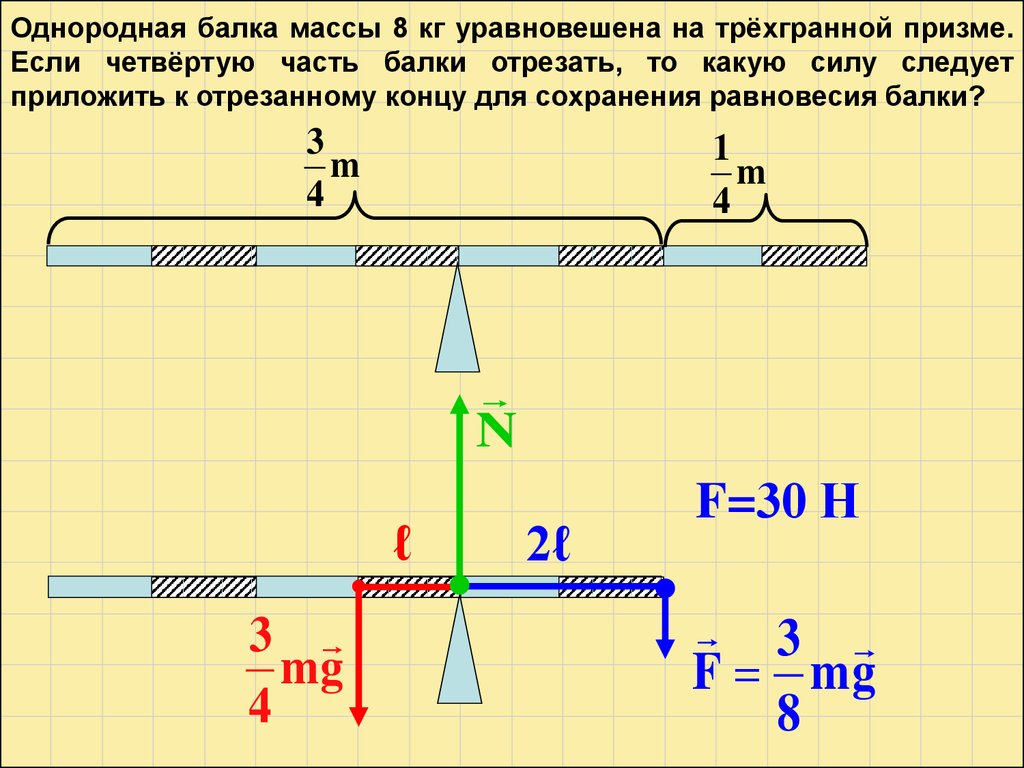
Однородная балка массы 8 кг уравновешена на трёхгранной призме.Если четвёртую часть балки отрезать, то какую силу следует
приложить к отрезанному концу для сохранения равновесия балки?
3
m
4
1
m
4
N
ℓ
3
mg
4
2ℓ
F=30 Н
3
F mg
8
20.
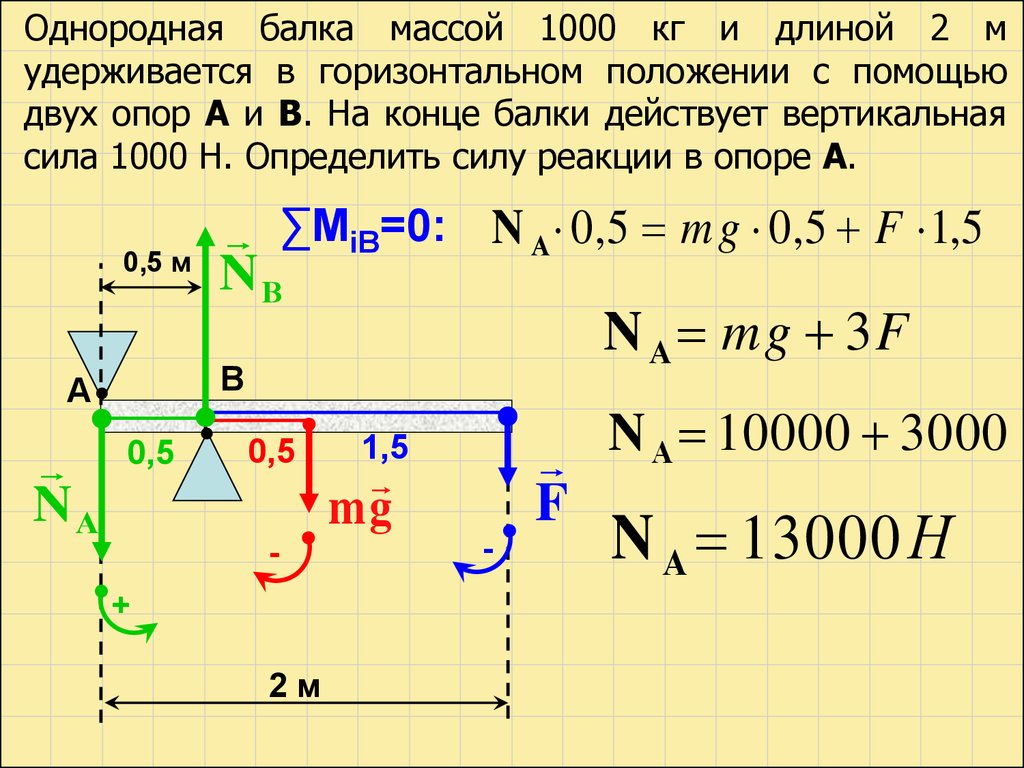
Однородная балка массой 1000 кг и длиной 2 мудерживается в горизонтальном положении с помощью
двух опор А и В. На конце балки действует вертикальная
сила 1000 Н. Определить силу реакции в опоре А.
0,5 м
N А mg 3 F
В
А
NА
∑МiВ=0: N А 0 ,5 m g 0 ,5 F 1,5
NВ
0,5
0,5
-
+
2м
N
10000
3000
А
F
1,5
mg
-
N А 13000 Н
21.
На однородный цилиндр навита веревка, конецкоторой закреплен в верхней точке наклонной
плоскости. Цилиндр расположен на наклонной
плоскости так, что веревка горизонтальна. Масса
цилиндра 10 кг. Найти модуль силы нормального
давления цилиндра на плоскость.
22.
∑Мiо=0:N mg N mg
ℓ
Т
О
N
ℓ
Fтр
mg
23.
1). ∑Мiо=0:N mg
2). Применим III H:
N mg
Р N mg 100 Н
N
Р
24.
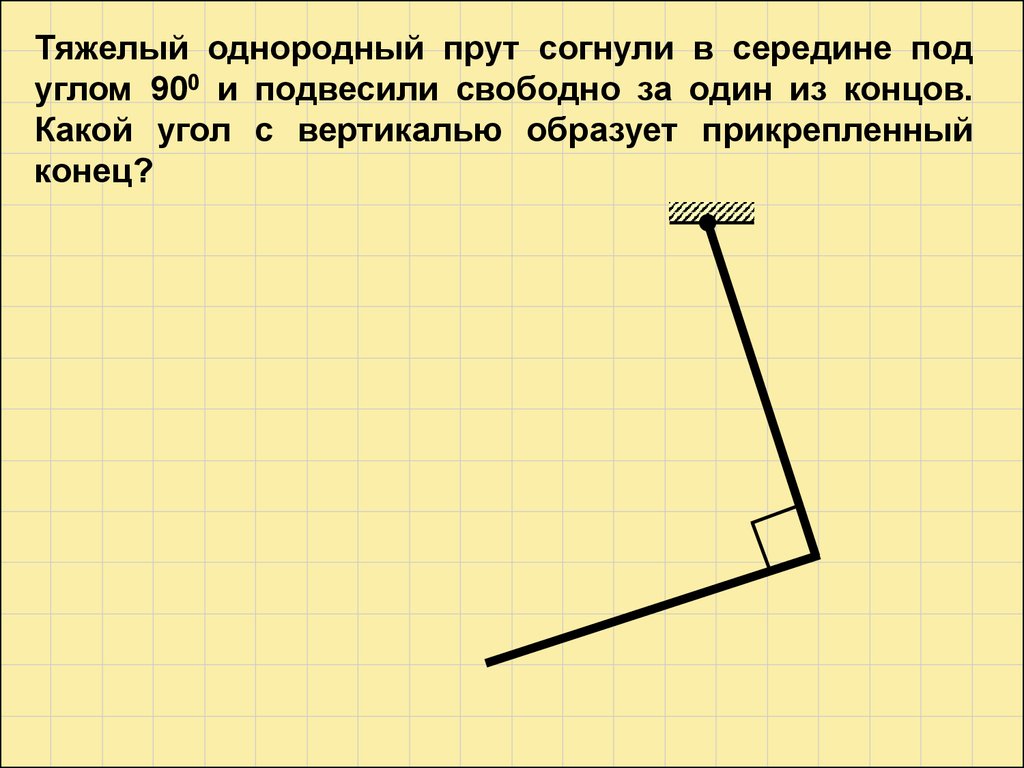
Тяжелый однородный прут согнули в середине подуглом 900 и подвесили свободно за один из концов.
Какой угол с вертикалью образует прикрепленный
конец?
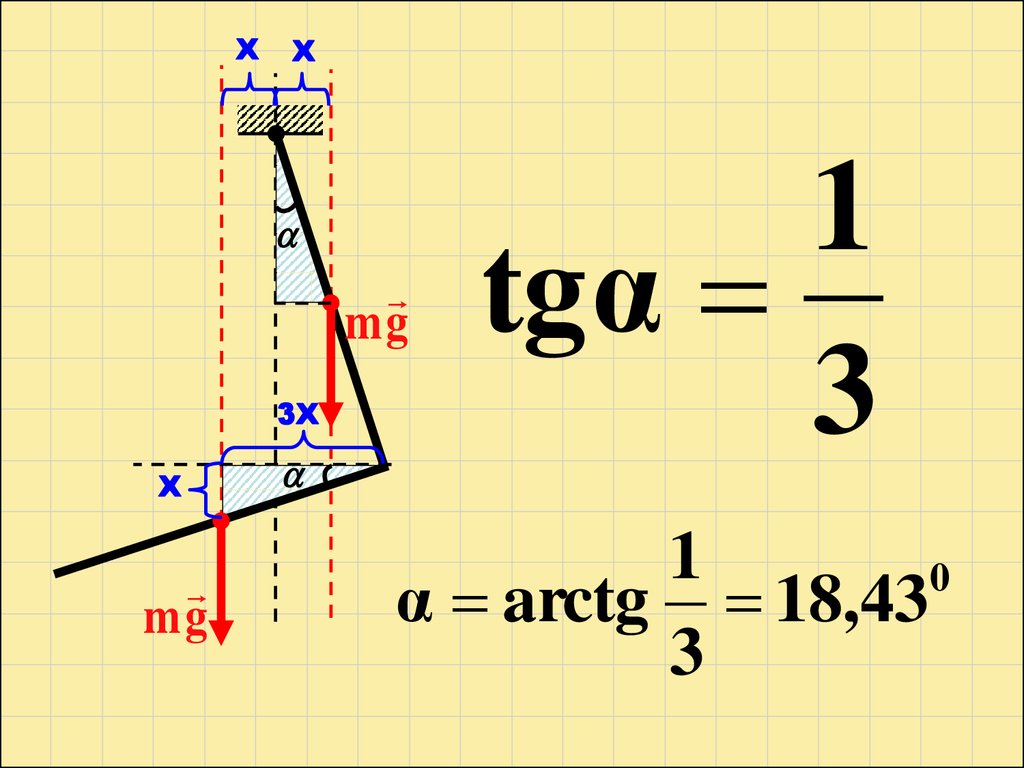
25.
XX
mg
3X
X
mg
1
tgα
3
1
0
α arctg 18,43
3
26.
D№ 324 (А.П. Рымкевич)
В
А
О
Стержень АО длиной 60 см, и массой 0,4 кг, укрепленный
шарнирно в точке О, поддерживается нитью АD.
Образующей угол 450 со стержнем. В точке В (АВ=20 см)
подвешен груз массой 0,6 кг. Найти силу натяжения нити и и
силу реакции в точке О.
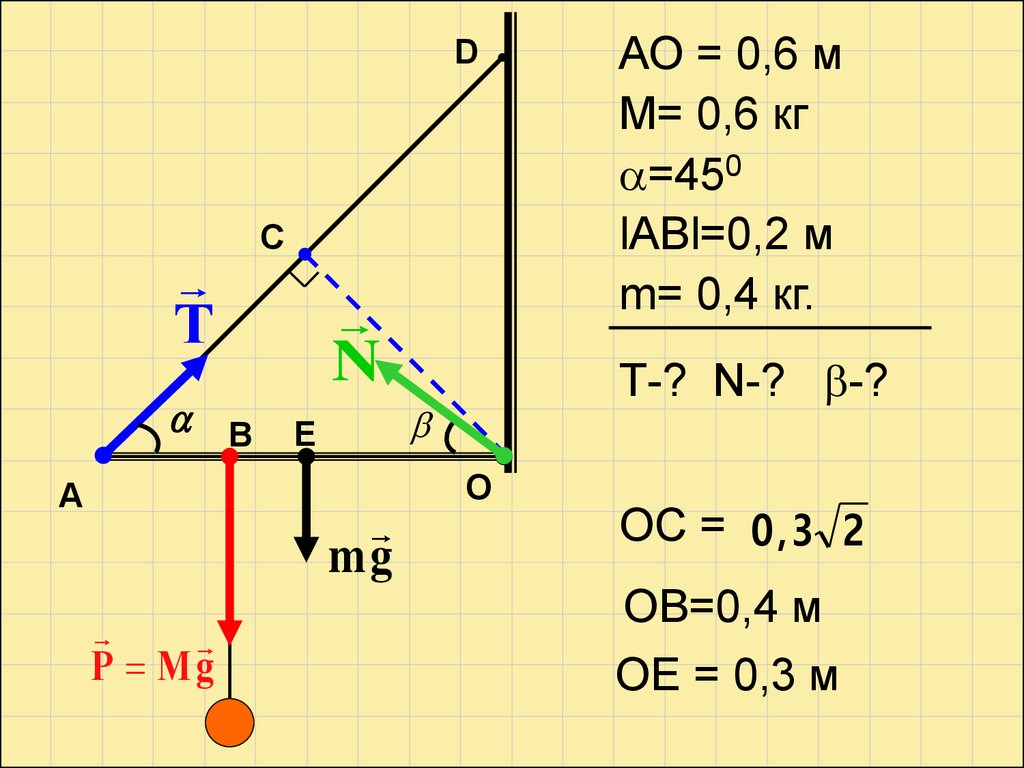
27.
DТ
C
В Е
А
N
Р Мg
Т-? N-? -?
mg
АО = 0,6 м
М= 0,6 кг
=450
lАВl=0,2 м
m= 0,4 кг.
О
ОС = 0,3 2
ОВ=0,4 м
ОЕ = 0,3 м
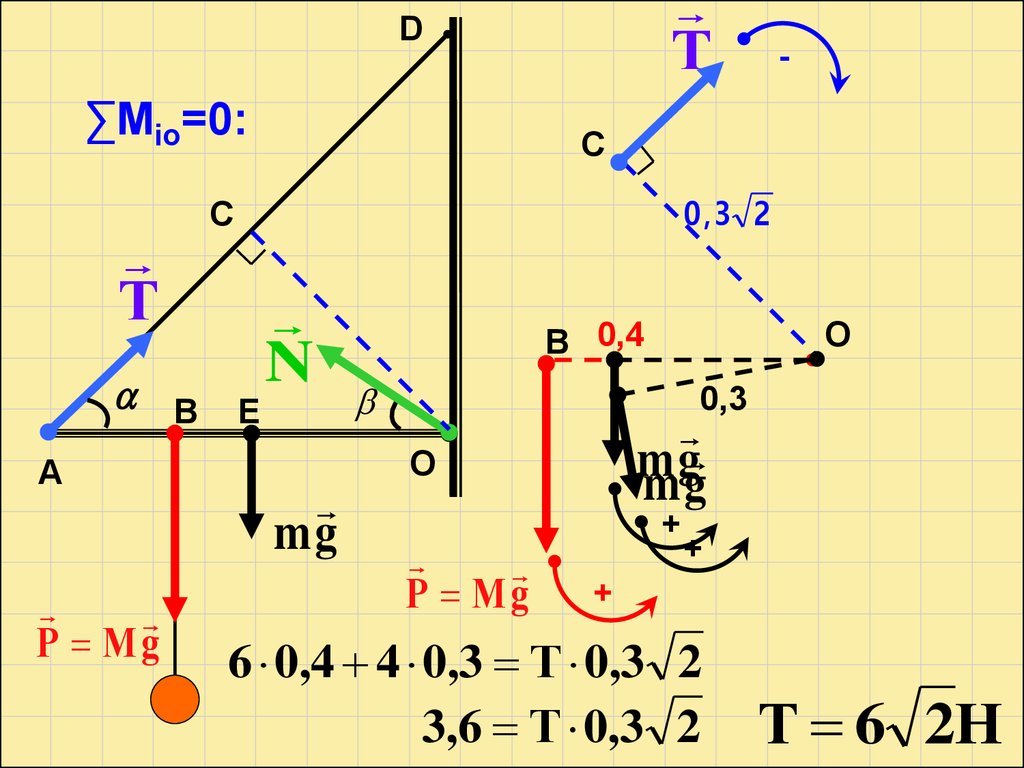
28.
ТD
∑Мiо=0:
А
Р Мg
C
0,3 2
C
Т
В
-
Е
N
mg
О
В 0,4
0,3
m
g
mg
О
Р Мg
+
+
+
6 0,4 4 0,3 Т 0,3 2
3,6 Т 0,3 2
Т 6 2Н
29.
Fy
ix
x
Т
Ncosβ Tcosα
Ncosβ 6Н (1)
N
F
iy
mg
Р Мg
0
(2) (1)
0
Nsinβ Tsinα (M m)g
Nsinβ (M m)g Tsinα
Nsinβ 10 6 4Н (2)
2
tgβ
3
β 33,7
0
30.
yNcosβ 6Н (1)
x
Nsinβ 10 6 4Н (2)
Т
N
mg
Р Мg
1
N (cos β sin β) 52
2
2
2
N 52 7,2Н
Ответы: N 7,2Н
Т 6 2Н
β 33,7
0
31.
При взвешивании на неравноплечих весах массатела на одной чашке получилась m1, а на другой m2. Определить истинную массу тела m.
ℓ1
m
ℓ1
m2
mℓ1=m1 ℓ2 (1)
m2ℓ1=m ℓ2 (2)
ℓ2
m1
ℓ2
m m1
(1):(2)
=
m2 m
m = m1 m 2
2
m
m = m1 m2
32.
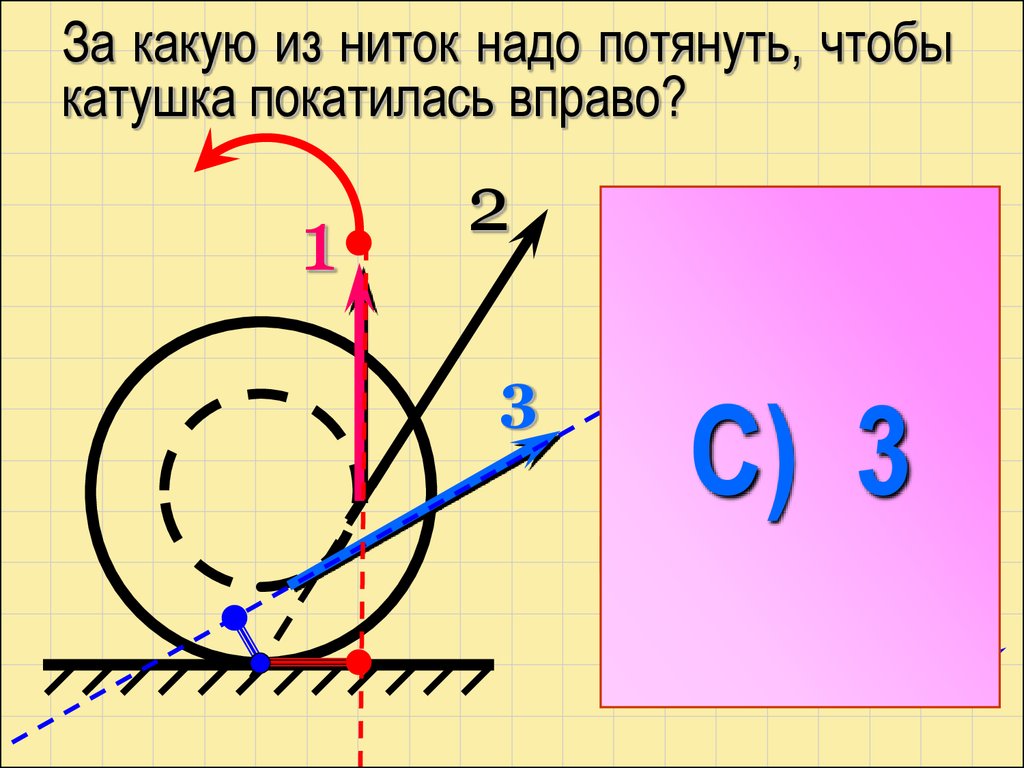
За какую из ниток надо потянуть, чтобыкатушка покатилась вправо?
1
2
3
А) 1
В) 1 или 2
С) 3
С) 3
D) За любую
Е) Катушка не может
покатиться вправо
33.
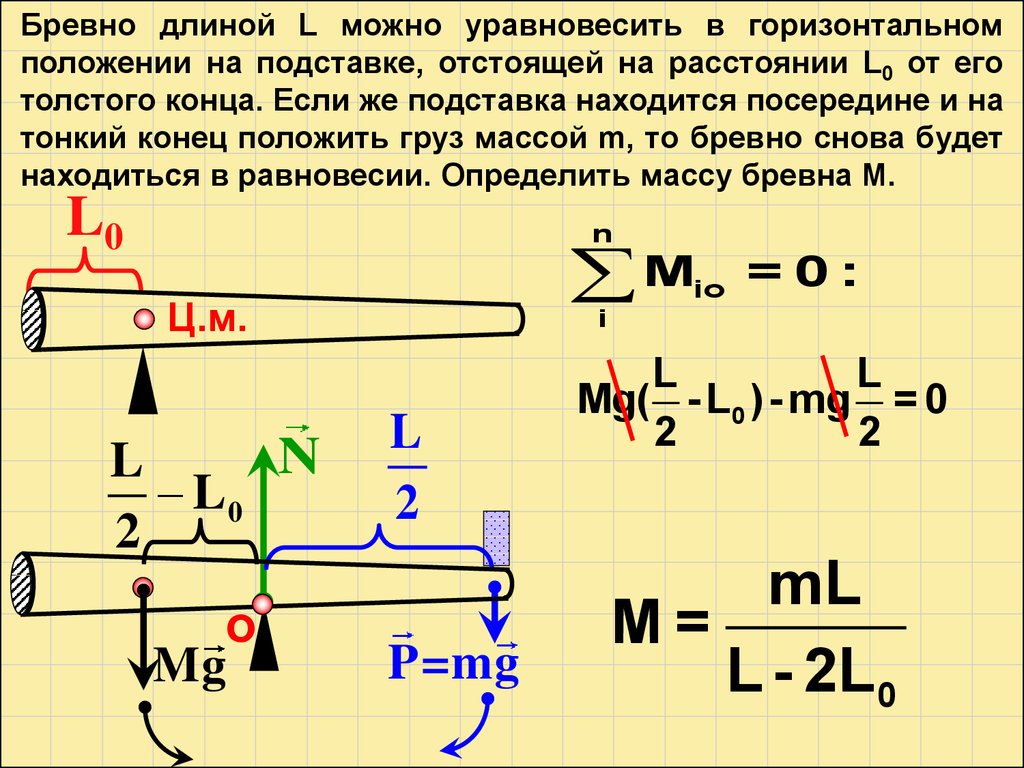
Бревно длиной L можно уравновесить в горизонтальномположении на подставке, отстоящей на расстоянии L0 от его
толстого конца. Если же подставка находится посередине и на
тонкий конец положить груз массой m, то бревно снова будет
находиться в равновесии. Определить массу бревна M.
L0
n
M
io
Ц.м.
N
L
L0
2
o
Mg
=0:
i
L
2
P=mg
L
L
Mg( - L0 ) - mg = 0
2
2
mL
M=
L - 2L0
34.
Бревно уравновешено на тросе. Какая часть бревнаокажется тяжелее, если его распилить в точке подвеса?
В) Правая
ℓл
ℓп
mл g
mп g
А) Левая В) Правая С) Массы равны
Фильм «Загадочный стержень»
35.
Два мальчика, массы которых m1 и m2 (m1> m2), сделалисебе качели, положив доску длиной L на упор
Определить массу доски m, считая ее однородной, если
известно, что она находится в равновесии, когда точка
опоры удалена на расстояние L0 (L0 < L/2) от одного из
концов, а мальчики сидят на концах доски
n
M
N
io
i
L0
=0 :
L
m1gL0 - mg( - L0 ) - m2g(L - L0 ) = 0
2
L
- L0
2
L-L0
o
P1 =m1g
mg P2 =m2g
L
m( - L0 ) = m1L0 - m2 (L - L0 )
2
m1L0 - m2 (L - L0 )
m=
L
L0
2
36.
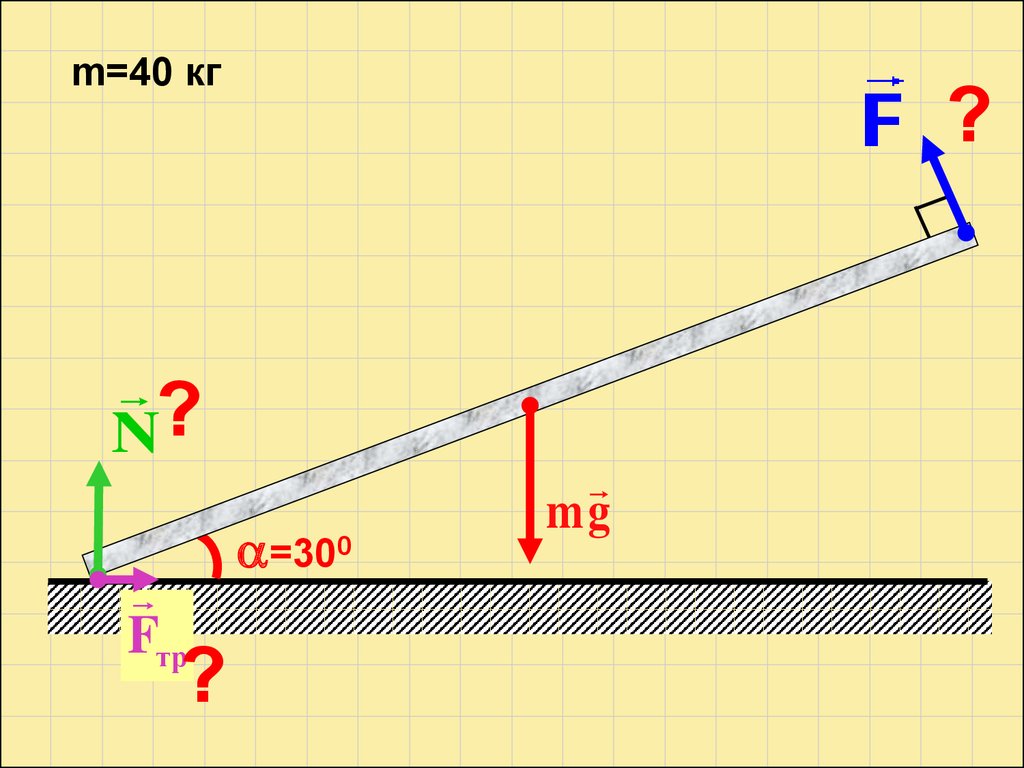
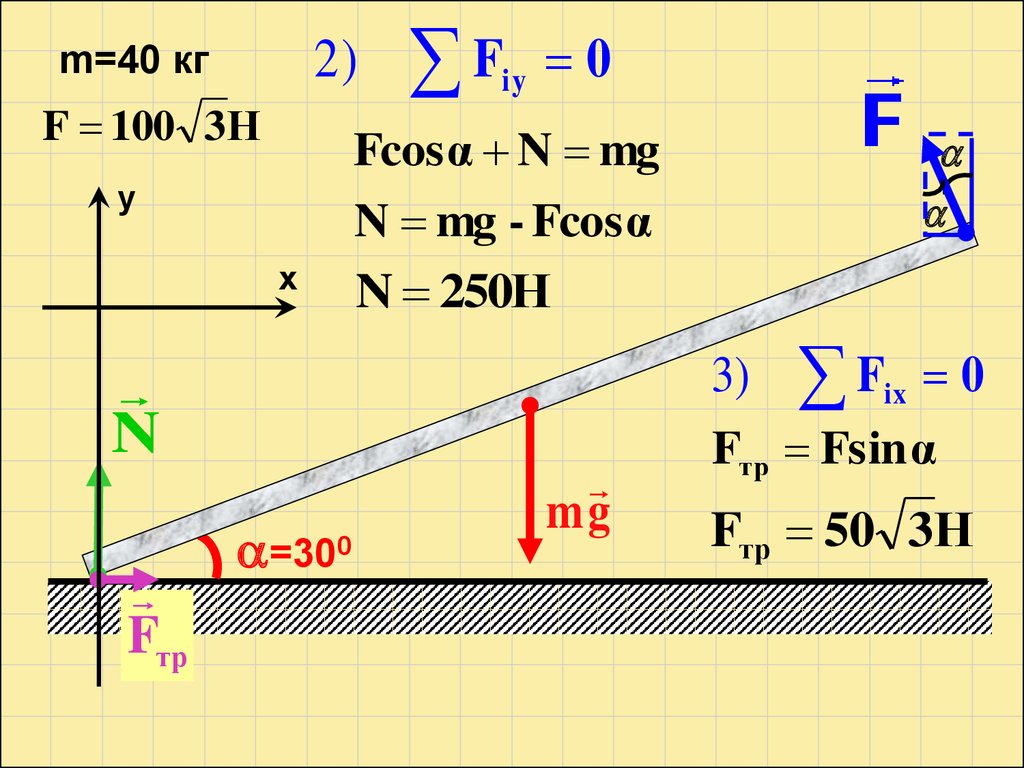
m=40 кгF ?
N?
Fтр
?
=300
mg
37.
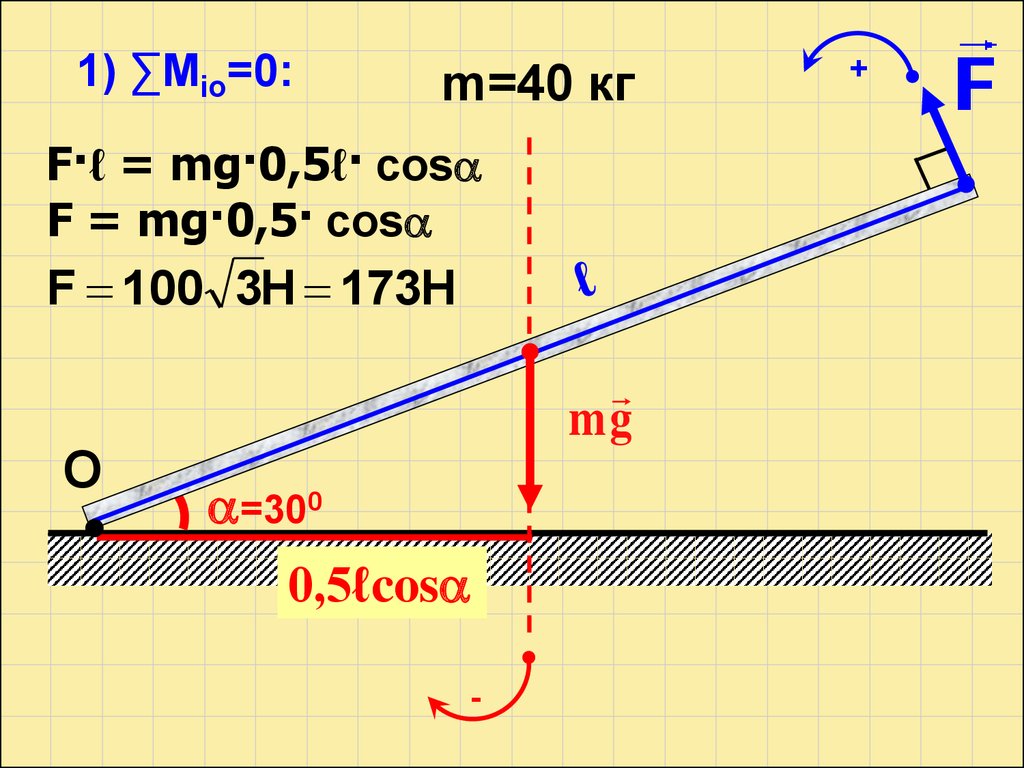
1) ∑Мiо=0:m=40 кг
F·ℓ = mg·0,5ℓ· cos
F = mg·0,5· cos
F 100 3Н 173Н
О
mg
=300
0,5ℓcos
-
+
F
38.
m=40 кг2)
F 100 3Н
iy
0
F
Fcosα N mg
N mg - Fcosα
y
x
N
Fтр
F
N 250Н
3)
=300
mg
F
ix
0
Fтр Fsinα
Fтр 50 3Н
39.
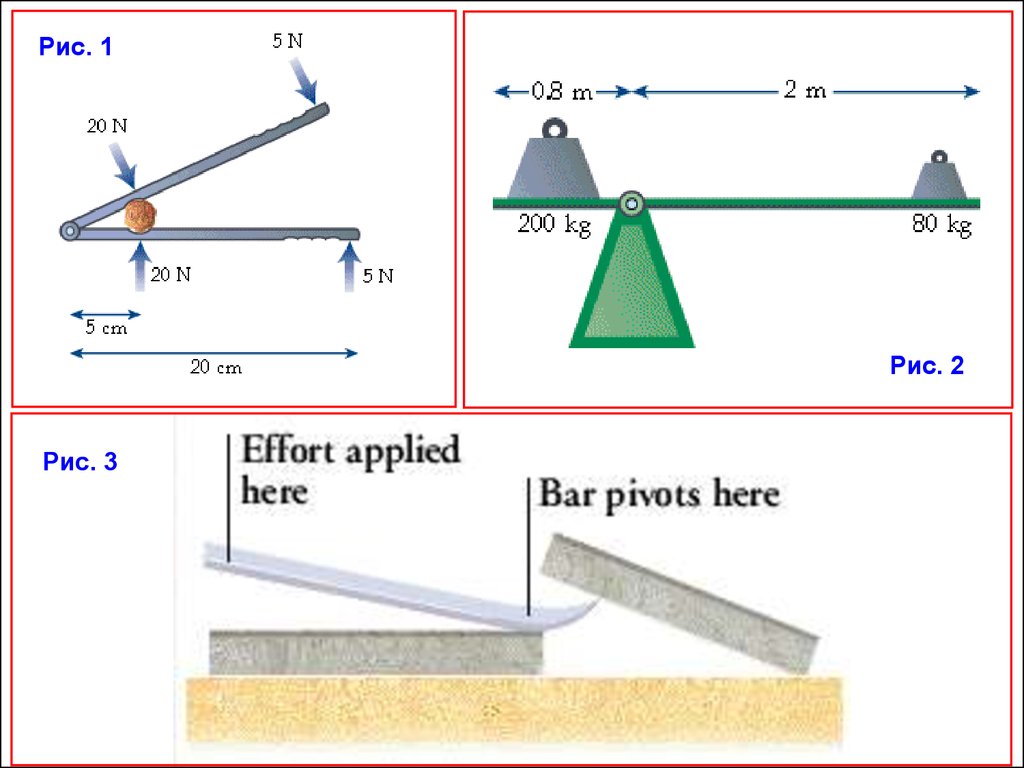
Рис. 1Рис. 2
Рис. 3
40.
Рис. 4Рис. 5
41.
42.
43.
44.
rF2
r
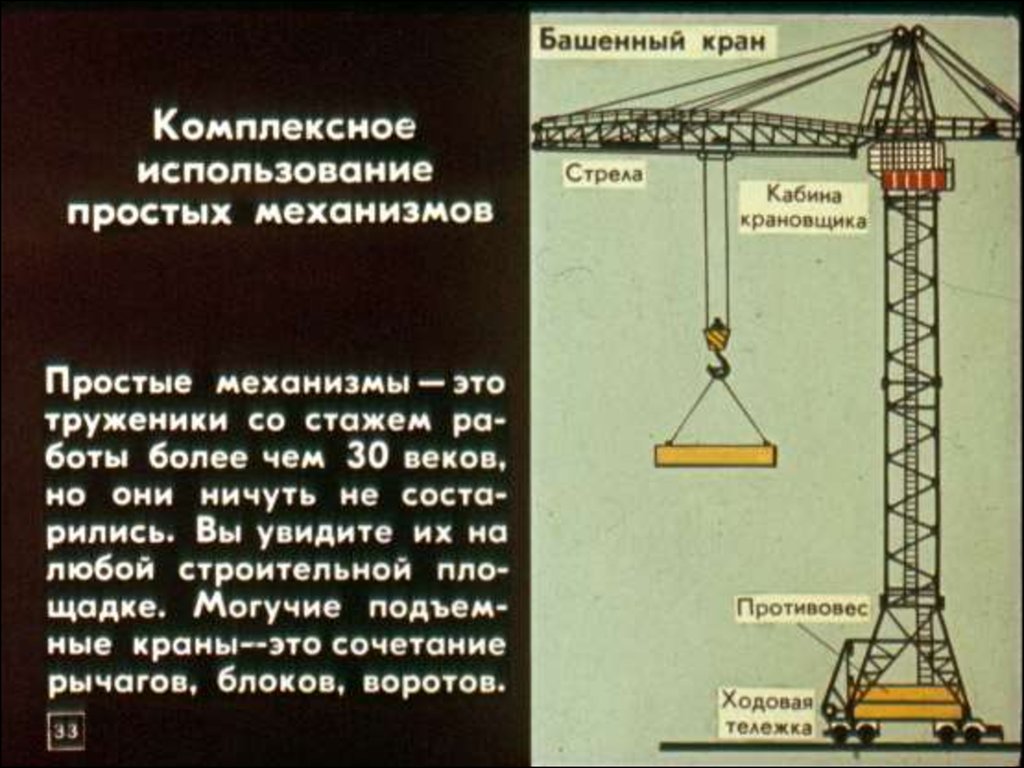
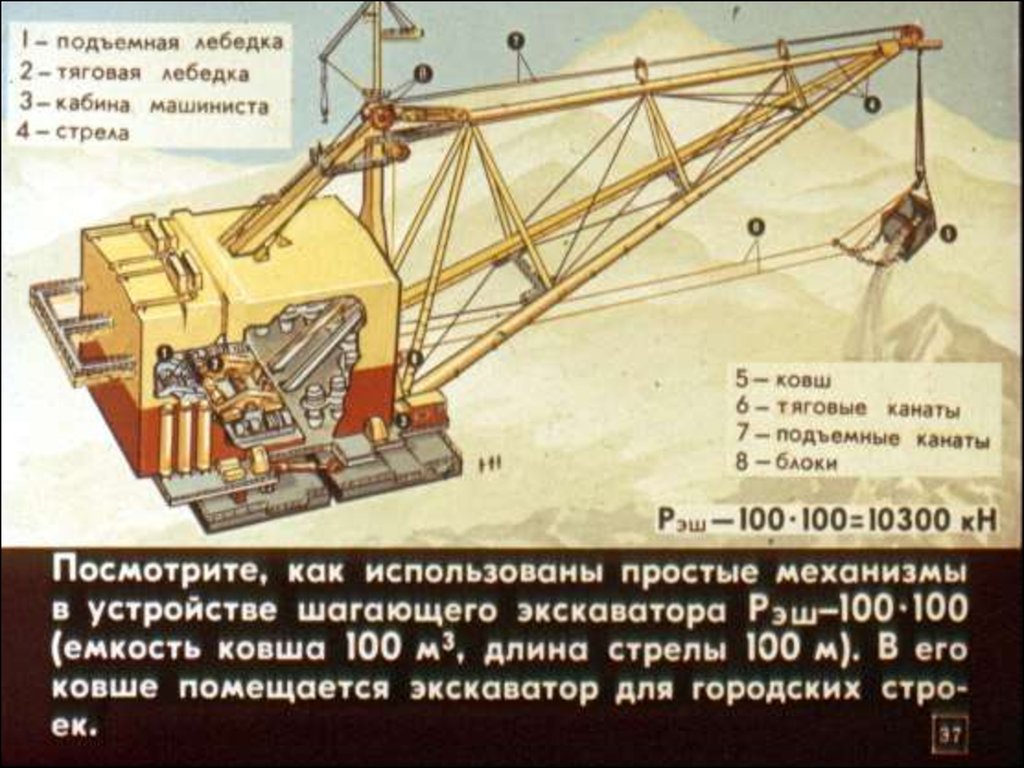
Подвижный блок Архимед принимал
за неравноплечий рычаг, дающий
выигрыш в силе в два раза.
2r
F1
2r
F1
F2



















 physics
physics








