Similar presentations:
Производная и дифференциал
1. Производная и дифференциал.
2.
• Первое правило Лопиталя (G.-F. de l’Hospital)0
(раскрытие неопределённости вида
)
0
Пусть функции f(x) и g(x) непрерывны и дифференцируемы
в окрестности точки х0 и равны нулю в этой точке
f(x0)=g(x0)=0.
Пусть g′(x)≠0 в окрестности точки х0. Тогда, если
существует предел отношения производных lim f ( x)
x x0 g ( x )
то существует и предел
формула:
f ( x)
lim
x x0 g ( x )
f ( x)
f ( x)
lim
lim
x x0 g ( x)
x x0 g ( x)
, причем справедлива
3. Теорема Лопиталя верна и в случае, когда
x , x , xЗамечание.
Если окажется, что отношение
производных
f ( x)
lim
x x0 g ( x )
снова представляет
собой неопределенность и f′(x) и g′(x)
удовлетворяют тем же требованиям, что и
функции f(x) и g(x), то правило Лопиталя
применяют повторно.
4. Пример 1. Найти
Пример 1.x 2 1 ln x
lim
x 1
ex e
Найти
x 1 ln x 0
x 1 ln x
lim
lim
x
x 1
x
e e
0 x 1
e e
2
2
1
2x
2 1 3
x
lim
x
x 1
e
e
e
5.
Пример 2.Найти
lim 2
x
arctan x
1 x 1
ln
2 x 1
1
arctan x
2
0
1
x
2
lim
lim
x
1 x 1
2
0 x 1 x 1
ln
2 x 1
2 x 1 x 1 2
1
1
2
2
2
x 1 x 1
1 x
0 1
x
lim
lim
lim
1
2
2
x 1 x x 1
x 1 x
x 1
0 1
1
x2
6.
Пример 3.Найти
x sin x
lim
x 0
x3
x sin x 0
x sin x
1 cos x 0
lim
lim
lim
3
2
x 0
x 0
3
x
3x
0 x 0
0
x
1 cos x
lim
x 0
3x
2
sin x 1
sin x 1
1
lim
lim
1
x 0 6 x
6 x 0 x
6
6
7.
• Второе правило Лопиталя(раскрытие неопределённости вида
)
Пусть функции f(x) и g(x) непрерывны и дифференцируемы
в окрестности точки х0, за исключением самой точки х0,
причем g′(x)≠0 .
Пусть
Тогда, если
lim f ( x) ,
x x0
lim g ( x)
x x0
существует предел отношения
f ( x)
f ( x)
производных lim
, то существует и предел lim
x x0 g ( x )
x x0 g ( x )
причем справедлива формула:
f ( x)
f ( x)
lim
lim
x x0 g ( x)
x x0 g ( x)
8.
Пример 4.ex
lim 2
x x
Найти
e
e
e
lim 2 lim
lim
x x
x x 2 x 2 x
x
x
x
e
lim
x
x
e
lim
x 2
x
2 x
9. Другие виды неопределённостей.
(0 , , 00 , 0 , 1 )Неопределённости вида
можно свести к
0
0
0 ,
и
, а затем
раскрыть с помощью правила Лопиталя.
10.
Пример 5.Найти
lim x ln x
x 0
ln x
ln x
lim x ln x 0 lim
lim
x 0
x 0 1
x 0 1
x
x
1 1
lim : 2 lim x 0
x 0 x
x 0
x
11.
Пример 6.Найти
1
lim
tan x
x cos x
2
sin x
1
1
lim
tan x lim
cos x
x cos x
x cos x
2
2
1 sin x 0
1 sin x
cos x
lim
lim
lim
lim cot x 0
cos x
0 x cos x
x
x sin x
x
2
2
2
2
12.
00
Неопределённости вида
0 , , 1
имеют место при рассмотрении функций
y f ( x) g ( x )
если при х→a функция f(x) стремится
соответственно к 0, 1 и ∞, а g(x)соответственно к 0, ∞ и 0.
Эти неопределённости с помощью тождества
f ( x) g ( x ) e g ( x ) ln f ( x )
сводятся к неопределённости вида 0 .
13.
Пример 7.Найти
lim x 0 lim e
x
x 0
0
ln x x
x 0
e
lim x
x 0
lim e x ln x
lim x ln x
x 0
x
x 0
0 e 1
см. пример 5
0
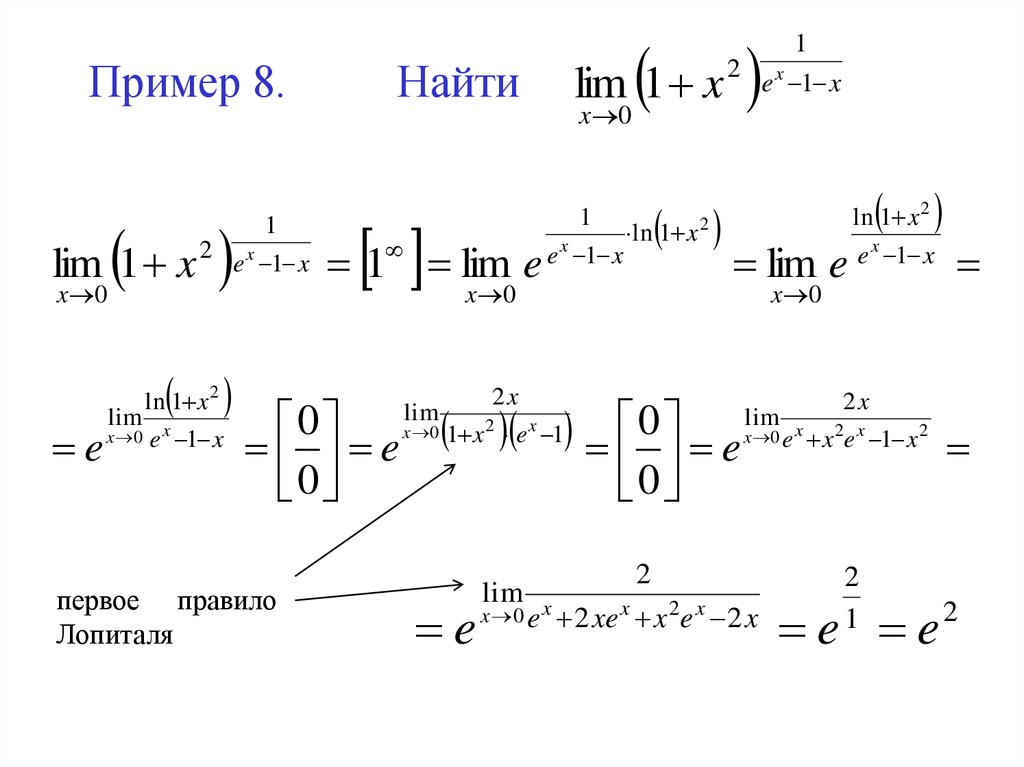
14.
Пример 8.lim 1 x
x 0
e
lim
x 0
2
ln 1 x 2
e x 1 x
1
e x 1 x
Найти
x 0
1
1 lim e
lim 1 x
e x 1 x
ln 1 x
x 0
2
2
1
e x 1 x
ln 1 x 2
lim e
e x 1 x
x 0
2x
2x
0 x 0 1 x2 e x 1 0 x 0 e x x2e x 1 x2
e
e
0
0
первое правило
Лопиталя
lim
e
lim
lim
2
x 0 e x 2 xe x x 2 e x 2 x
2
1
e e
2
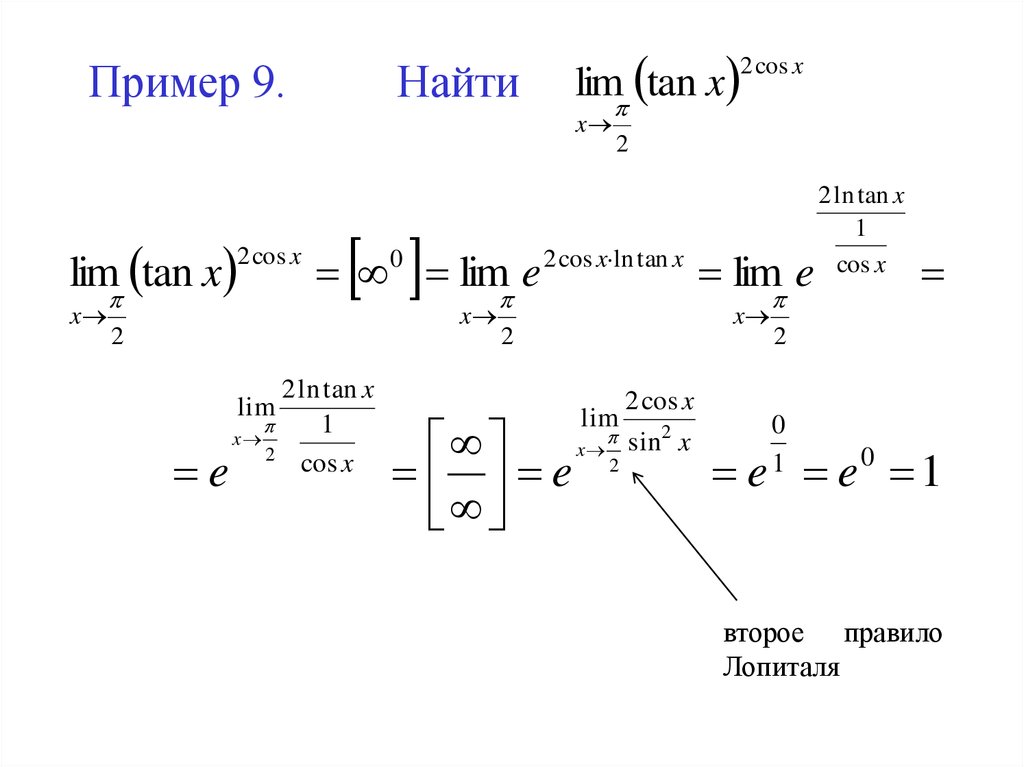
15.
Пример 9.Найти
2 cos x
lim tan x
x
lim tan x
2 cos x
x
0 lim e 2 cos x ln tan x lim e
2
2 ln tan x
1
x
2
cos x
lim
e
2
x
x
2
lim
x
e 2
2 cos x
sin2 x
2 ln tan x
1
cos x
2
0
1
e e 1
0
второе правило
Лопиталя













 mathematics
mathematics








