Расположение плоскости, в зависимости от коэффициентов уравнения

1.

Расположение плоскости, в зависимости от
коэффициентов уравнения.
1) А 0. Вy Cz D 0 плоскость, параллельная оси Оx
Вектор
N (0; B; C ) перпендикулярен оси Оx.

2.

2) В = 0. Ax Cz D 0 плоскость, параллельная оси Оy
Вектор N ( A; 0; C ) перпендикулярен оси Оy.

3.

3) С = 0. Ax By D 0 плоскость, параллельная оси Oz.
Вектор N ( A; B; 0) перпендикулярен оси Оz.

4.

4) А = 0, В = 0.
Сz D 0
xOy,
плоскость, параллельная плоскости
так как эта плоскость параллельна двум осям – Ox
и
Oy.

5.

5) А = 0, С = 0.
плоскость, параллельная плоскости
так как эта плоскость параллельна двум осям –
Ox
и
By D 0
xOz,
Oz.

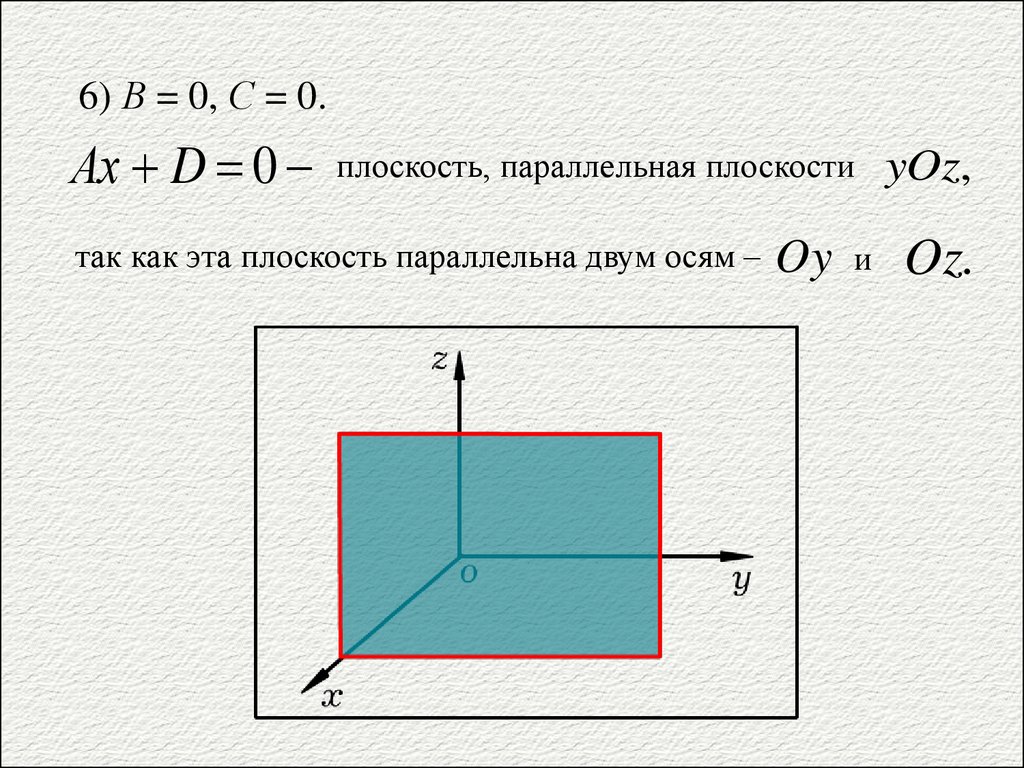
6.

6) В = 0, С = 0.
плоскость, параллельная плоскости
так как эта плоскость параллельна двум осям –
Oy
и
Аx D 0
yOz,
Oz.

7.

7) А = 0, D = 0.
By Сz 0
плоскость,
проходящая через
ось Ox,
так как она параллельна оси
Ox
и проходит через начало координат.
8) В = 0, D = 0.
плоскость,
Ax Сz 0 проходящая через
ось Oy,
так как она параллельна оси Oy
и проходит через начало координат.

8.

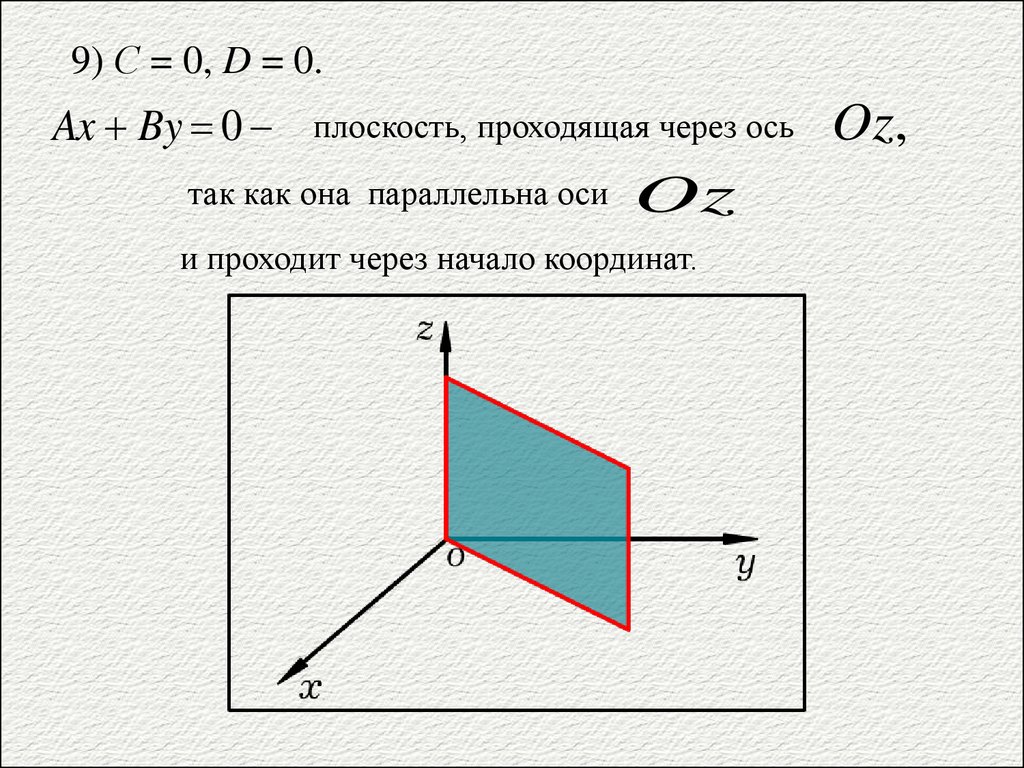
9) С = 0, D = 0.
Ax By 0
плоскость, проходящая через ось
так как она параллельна оси
Oz
и проходит через начало координат.
Oz,

9.

10) А = 0, В = 0, D = 0.
Сz 0 или z 0 координатная плоскость
xOy.
11) А = 0, С = 0, D = 0.
Dy 0 или y 0
координатная плоскость
12) В = 0, С = 0, D = 0.
Ax 0 или x 0 координатная плоскость
xOz.
yOz.
13) D = 0.
Ax By Сz 0
плоскость, проходящая через начало координат.

10.

3.1.3. Уравнение плоскости в отрезках на осях
имеет вид
x y z
1,
a b c
им удобно пользоваться при построении плоскости.

11.

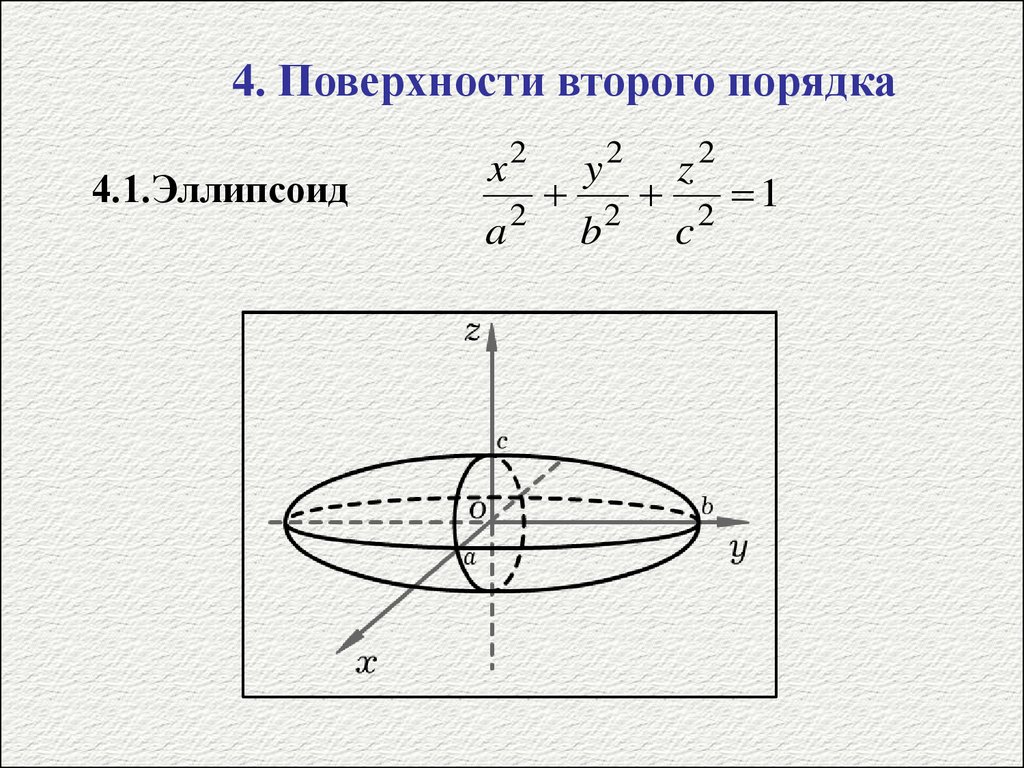
4. Поверхности второго порядка
4.1.Эллипсоид
x2
a
2
y2
b
2
z2
c
2
1

12.

2
2
2
x
y
z
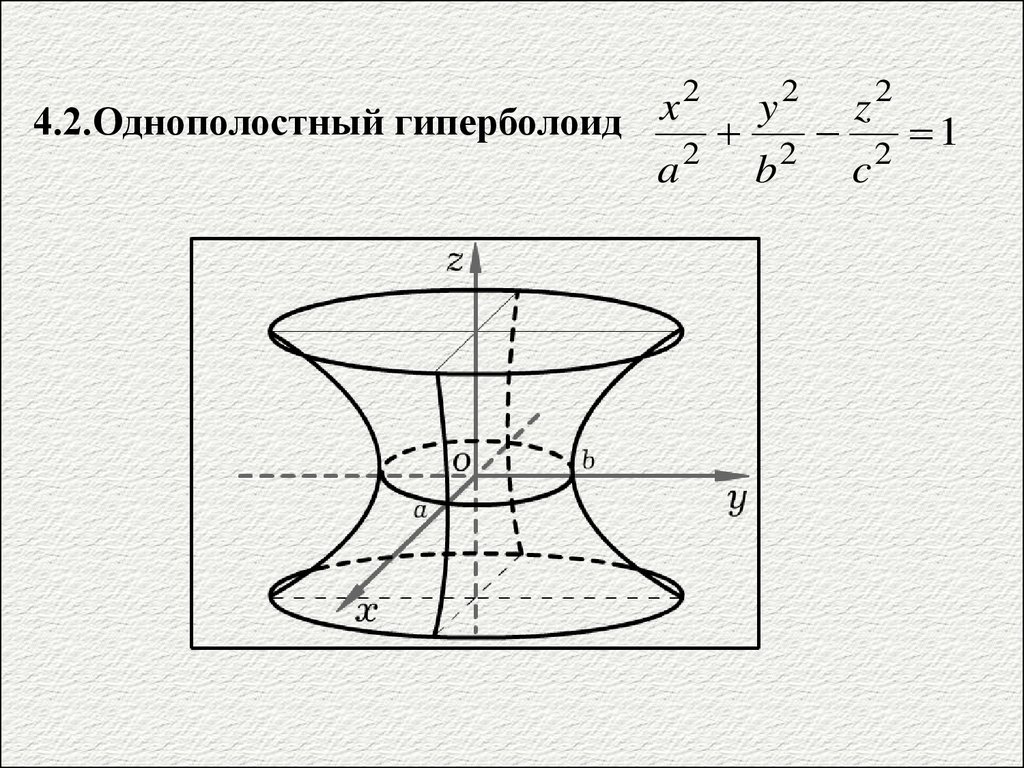
4.2.Однополостный гиперболоид
2 2 1
2
a
b
c

13.

4.3. Двуполостный гиперболоид
x2
a2
y2
b2
z2
c2
1

14.

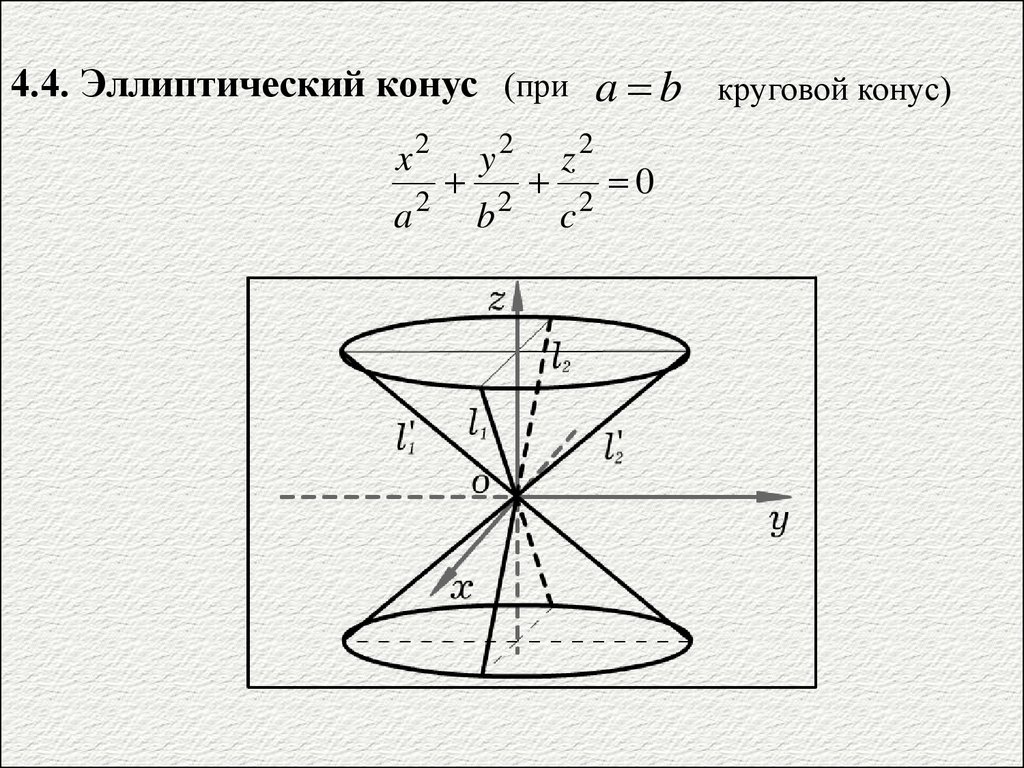
4.4. Эллиптический конус (при a b круговой конус)
x2
a2
y2
b2
z2
c2
0

15.

4.5. Эллиптический параболоид
x2 y2
2z
p
q

16.

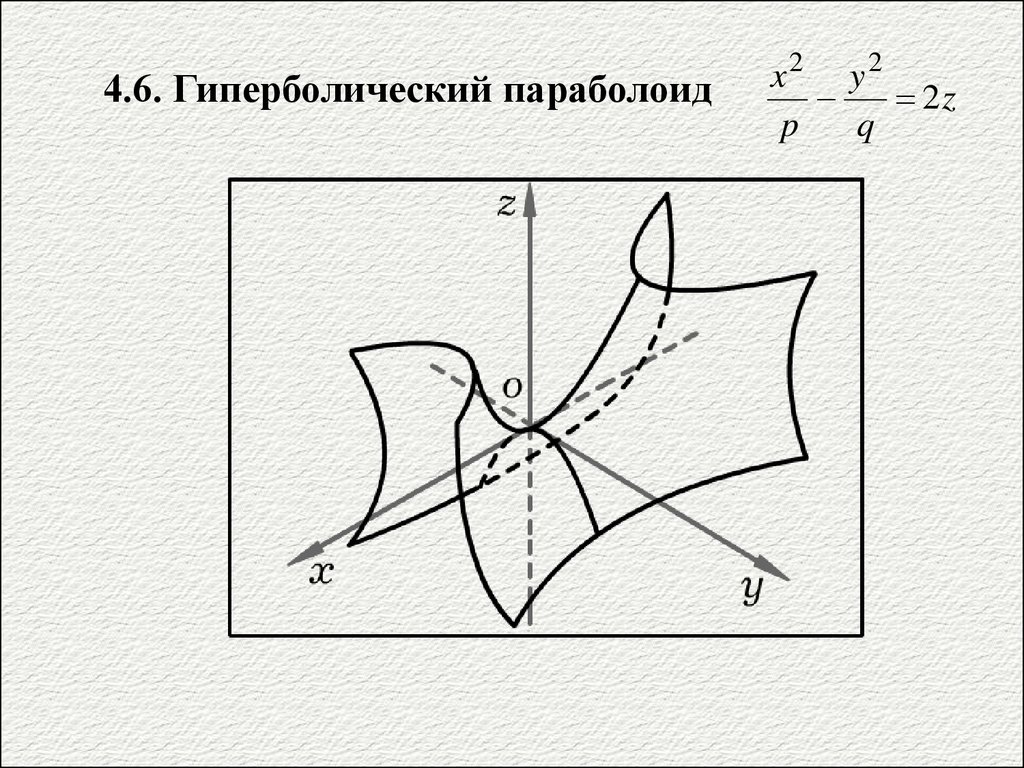
4.6. Гиперболический параболоид
x2 y2
2z
p
q

17.

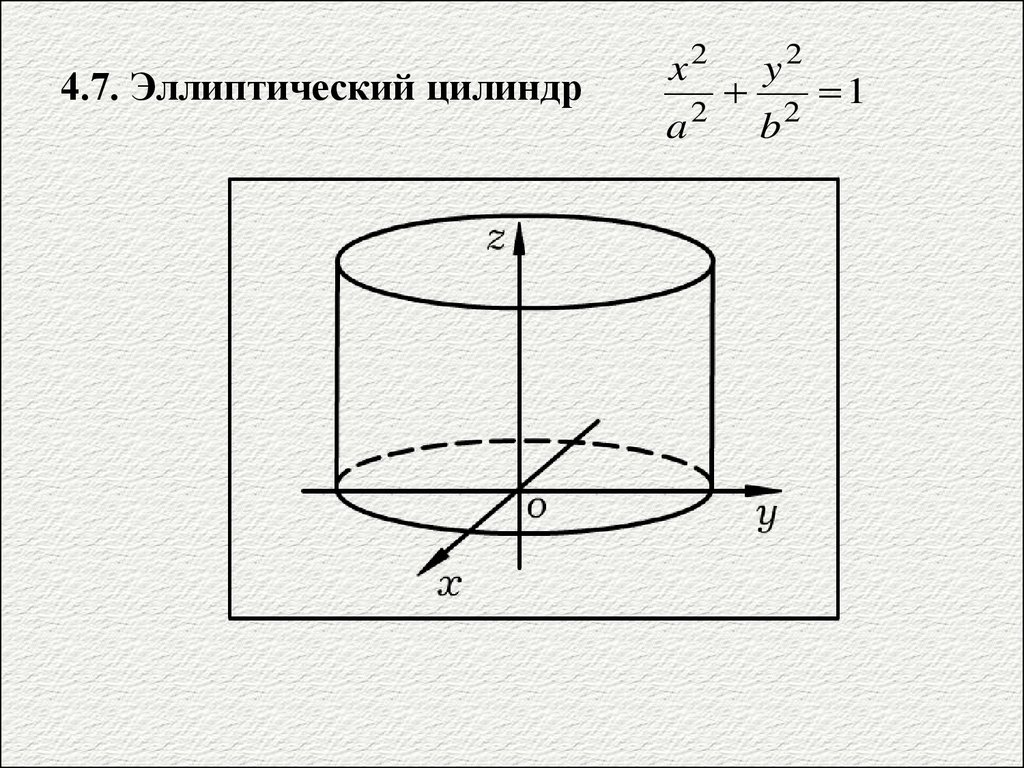
4.7. Эллиптический цилиндр
x2
a
2
y2
b
2
1

18.

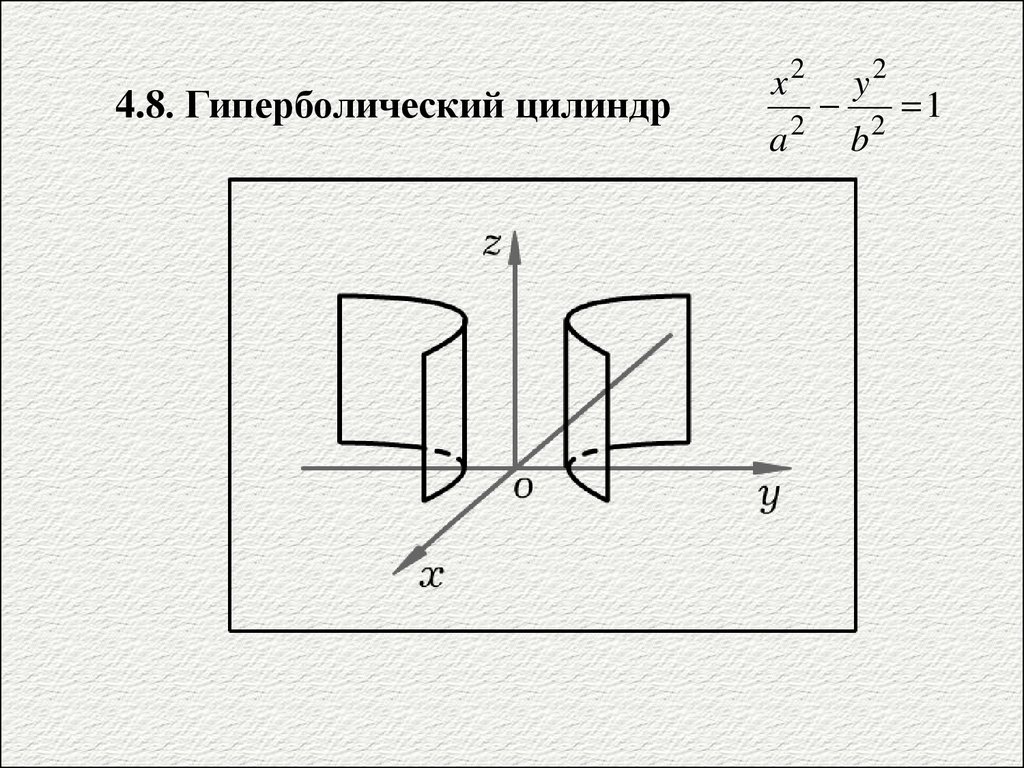
4.8. Гиперболический цилиндр
x2
a
2
y2
b
2
1

19.

4.9. Параболический цилиндр
x 2 py
2