Поверхности второго порядка

1. Поверхности второго порядка

Поверхности вращения
Канонические уравнения поверхностей второго порядка
Цилиндрические
поверхности
параллельными координатным осям
с
образующими,

2. Поверхности вращения

3. Поверхности вращения

4. Поверхности вращения

Рассмотрим поверхность вращения, заданную уравнением
F ( x 2 y 2; z) 0
Правило
Для построения этой поверхности задаем x = 0, рисуем линию
на плоскости YOZ с уравнением F ( y 2 ; z ) 0 , затем
вращаем ее вокруг оси OZ.
Аналогично изображаются поверхности:
F ( x 2 z2; y ) 0
(задаем x = 0, рисуем линию на плоскости
YOZ , затем вращаем ее вокруг оси OY )
F (y 2 z2; x ) 0
(задаем y = 0, рисуем линию на плоскости
XOZ , затем вращаем ее вокруг оси OX )

5. Поверхности вращения

z x2 y 2
Пример 1
Зададим x = 0, и получим уравнение линии на плоскости YOZ:
z y
2
z
параболоид
вращения
0
x
y

6. Поверхности вращения

z2 x 2 y 2
Пример 2
Зададим x = 0, и получим уравнение линии на плоскости YOZ:
z2 y 2
z y
- уравнения двух прямых
z
конус
0
x
y

7. Поверхности вращения

x 2 y 2 z2 R 2
Пример 3
Зададим x = 0, и получим уравнение линии на плоскости YOZ:
y 2 z2 R 2
- уравнение окружности
z
сфера
0
y
x
В общем случае уравнение сферы с центром в точке (a; b; c) и
2
2
2
x a y b z c R2
радиусом R:

8. Канонические уравнения поверхностей второго порядка

Поверхности второго порядка делятся на
1) вырожденные
и
2) невырожденные
Вырожденные поверхности второго порядка это плоскости и точки,
которые задаются уравнением второго порядка. Если уравнению
второго порядка не удовлетворяет ни одна точка пространства, то
тоже говорят, что уравнение определяет вырожденную поверхность
(мнимую поверхность второго порядка).
Невырожденные поверхности второго порядка подразделяются на пять
типов.

9. Канонические уравнения поверхностей второго порядка

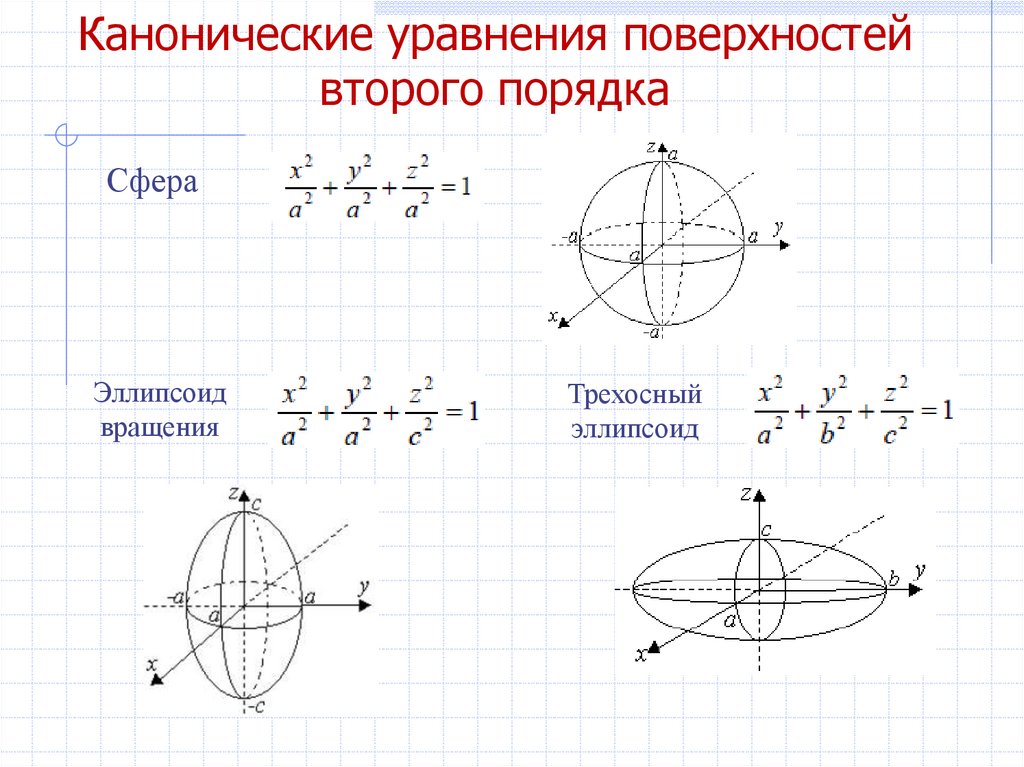
1
Эллипсоид
Эллипсоидом называется геометрическое место точек
пространства, координаты которых в некоторой
декартовой системе координат удовлетворяют
уравнению:
где a, b, c – положительные константы.
Величины a, b и c называются полуосями эллипсоида.
Если все они различны, то эллипсоид называется трехосным.
Если две из трех полуосей равны, эллипсоид является поверхностью
вращения. Он получается в результате вращения эллипса вокруг одной из
своих осей.
Эллипсоид, у которого все три полуоси равны, называют сферой.

10. Канонические уравнения поверхностей второго порядка

Сфера
Эллипсоид
вращения
Трехосный
эллипсоид

11. Канонические уравнения поверхностей второго порядка

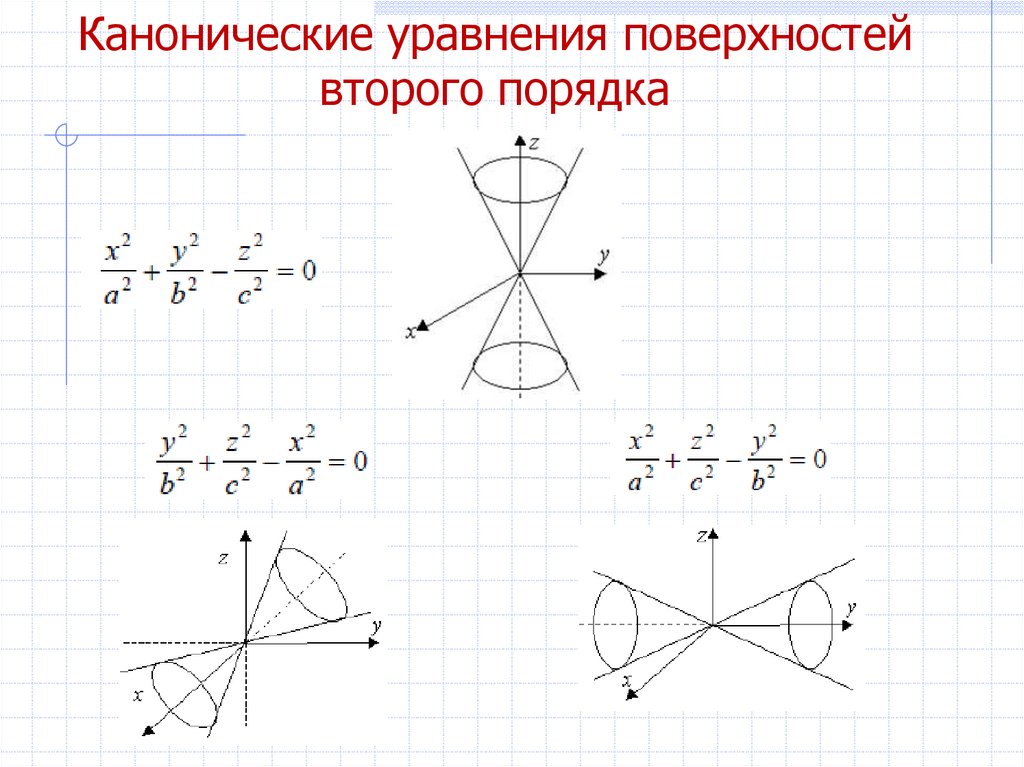
2
Конус второго порядка
Конусом называется геометрическое место точек
пространства, координаты которых в некоторой
декартовой системе координат удовлетворяют
уравнению
где a, b, c – положительные константы.
Величины a, b и c называются полуосями конуса. Центр симметрии
O называется вершиной конуса.
Если a = b, то конус является поверхностью вращения. Он получается в
результате вращения прямой
c
z y
b
вокруг оси Oz .

12. Канонические уравнения поверхностей второго порядка

13. Канонические уравнения поверхностей второго порядка

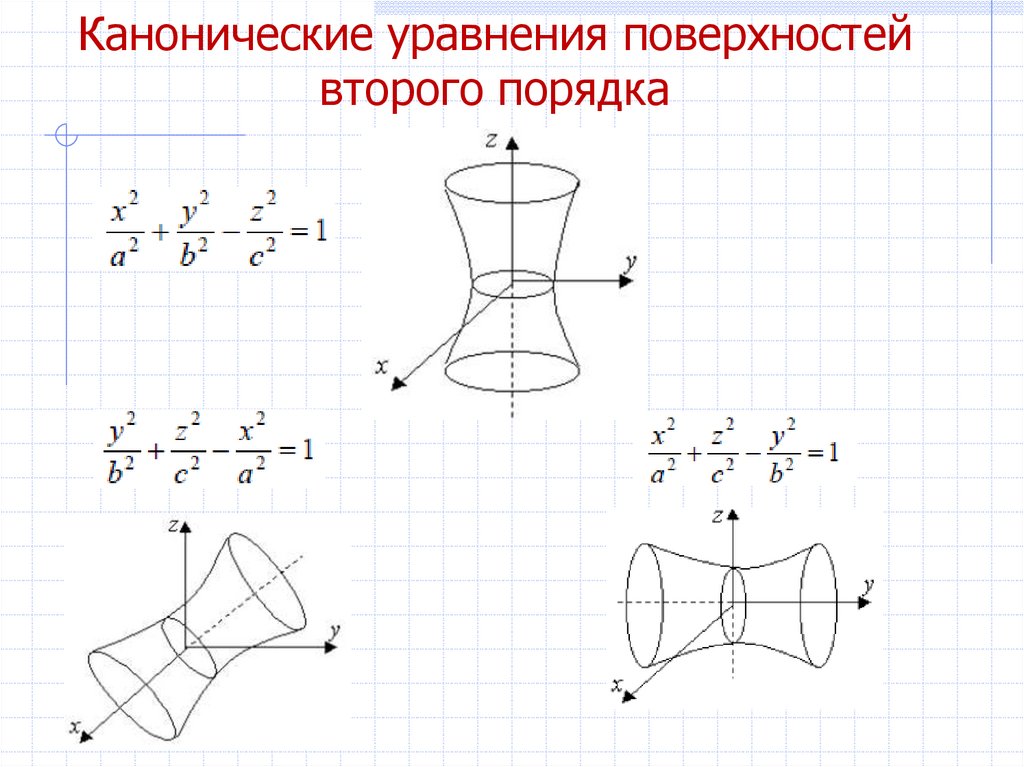
3
Гиперболоиды
Однополостным
гиперболоидом
называется
геометрическое
место
точек
пространства,
координаты которых в некоторой декартовой системе
координат удовлетворяют уравнению
где a, b, c – положительные константы.
Величины a, b и c называются полуосями однополостного
гиперболоида.
Если a = b, то однополостный гиперболоид является поверхностью
вращения. Он получается в результате вращения гиперболы
y2 z2
2 1 вокруг своей мнимой оси.
2
b
c

14. Канонические уравнения поверхностей второго порядка

15. Канонические уравнения поверхностей второго порядка

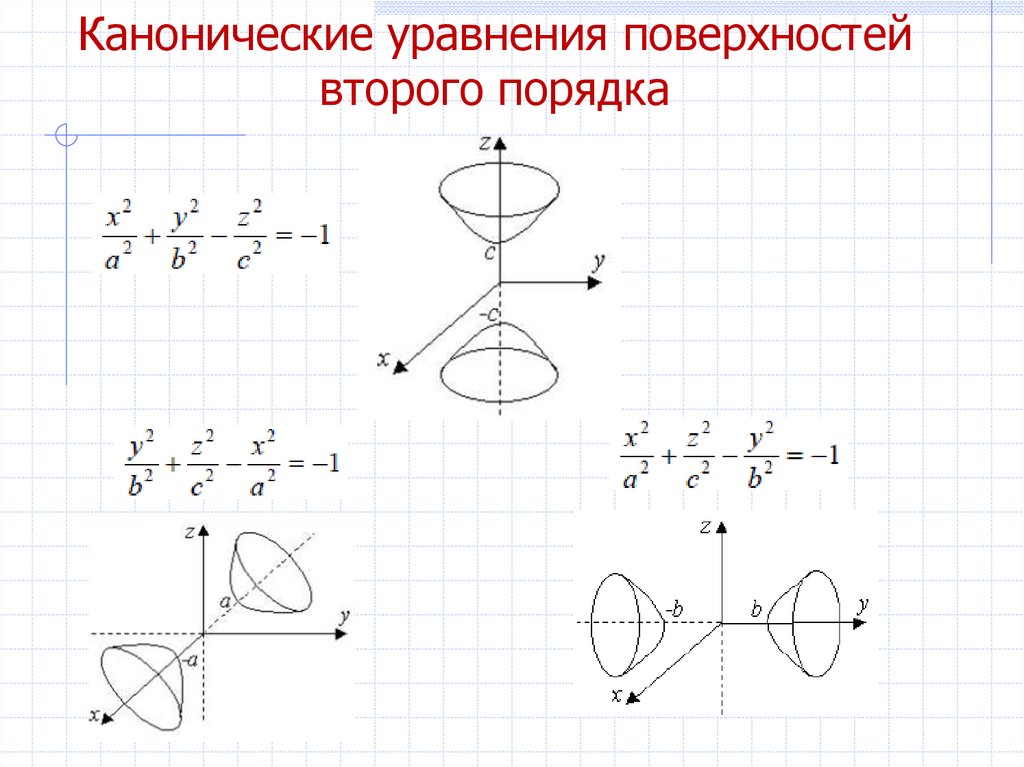
Двуполостным
гиперболоидом
называется
геометрическое
место
точек
пространства,
координаты которых в некоторой декартовой системе
координат удовлетворяют уравнению
где a, b, c – положительные константы.
Величины
a, b
и
c
называются полуосями двуполостного
гиперболоида.
Если a = b, то двуполостный гиперболоид является поверхностью
вращения. Он получается в результате вращения гиперболы
y2 z2
2 2 1
b
c
вокруг своей действительной оси.

16. Канонические уравнения поверхностей второго порядка

17. Канонические уравнения поверхностей второго порядка

4
Параболоиды
Эллиптическим
параболоидом
называется
геометрическое
место
точек
пространства,
координаты которых в некоторой декартовой системе
координат удовлетворяют уравнению
x2 y2
2 2z ,
2
a
b
где a, b – положительные константы.
Величины a и b называются параметрами параболоида. Точка O
называется вершиной параболоида.
Если a = b, то параболоид является поверхностью вращения. Он
получается в результате вращения параболы
y 2 2b 2 z вокруг оси Oz.

18. Канонические уравнения поверхностей второго порядка

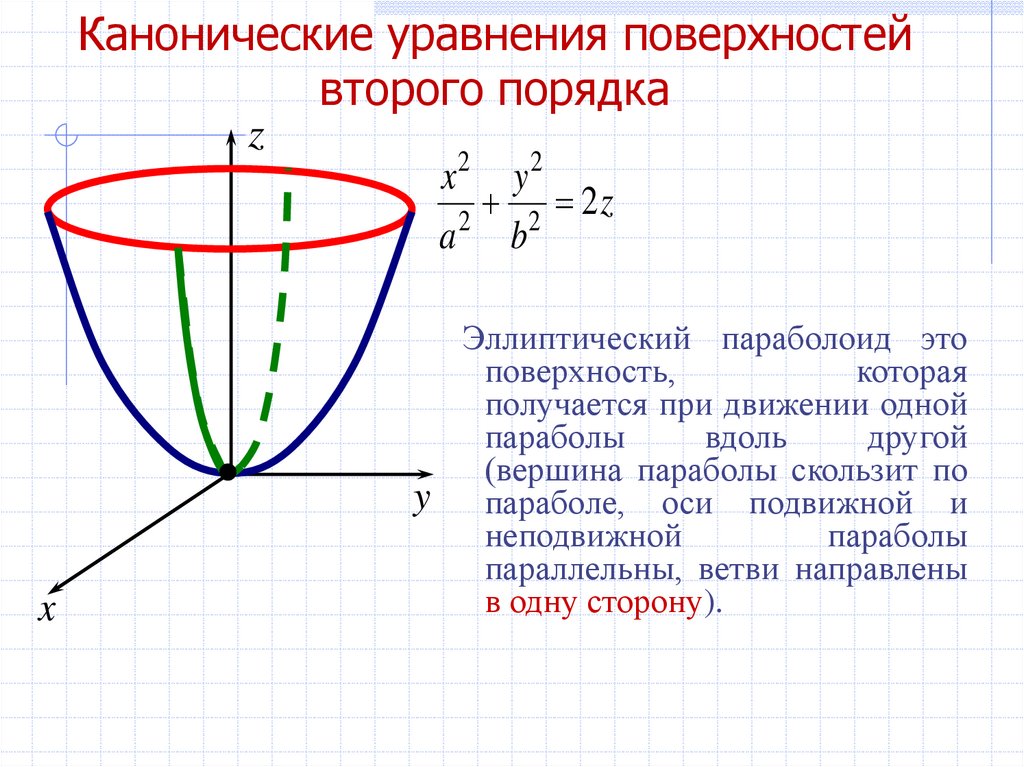
z
x
x2 y2
2 2z
2
a b
Эллиптический параболоид это
поверхность,
которая
получается при движении одной
параболы
вдоль
другой
(вершина параболы скользит по
y параболе, оси подвижной и
неподвижной
параболы
параллельны, ветви направлены
в одну сторону).

19. Канонические уравнения поверхностей второго порядка

Замечания: 1) Уравнение
x2 y 2
2 2 z
2
a
b
тоже определяет эллиптический
«развернутый» вниз.
параболоид,
2
2
2
2
x
z
y
z
2) Уравнения
2 2 y и 2 2 2 x
2
a
c
b
c
определяют эллиптические параболоиды, с
симметрии Oy и Ox соответственно.
но
осями

20. Канонические уравнения поверхностей второго порядка

Гиперболическим
параболоидом
называется
геометрическое
место
точек
пространства,
координаты которых в некоторой декартовой системе
координат удовлетворяют уравнению
x2 y2
2 2z ,
2
a b
где a, b – положительные константы.
Величины a и b называются параметрами параболоида.

21. Канонические уравнения поверхностей второго порядка

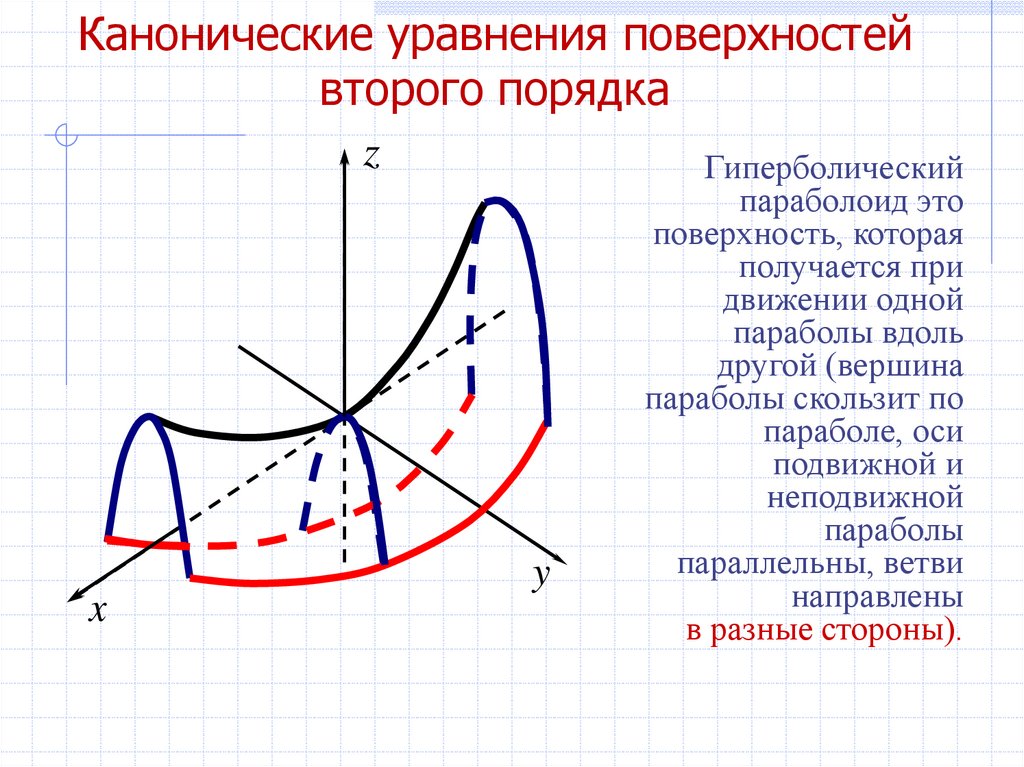
z
x
y
Гиперболический
параболоид это
поверхность, которая
получается при
движении одной
параболы вдоль
другой (вершина
параболы скользит по
параболе, оси
подвижной и
неподвижной
параболы
параллельны, ветви
направлены
в разные стороны).

22. Канонические уравнения поверхностей второго порядка

2
2
x
y
Замечания: 1) Уравнение
2 2 z
2
a
b
тоже определяет параболоид, но «развернутый» вниз.
z 2 x2
y2 z2
2) Уравнения 2 2 2 y и 2 2 2 x
c
a
b
c
определяют параболоиды, «вытянутые» вдоль осей Oz и
Oy соответственно.
3) Уравнение вида
также определяет гиперболический
параболоид

23. Канонические уравнения поверхностей второго порядка

5
Цилиндры
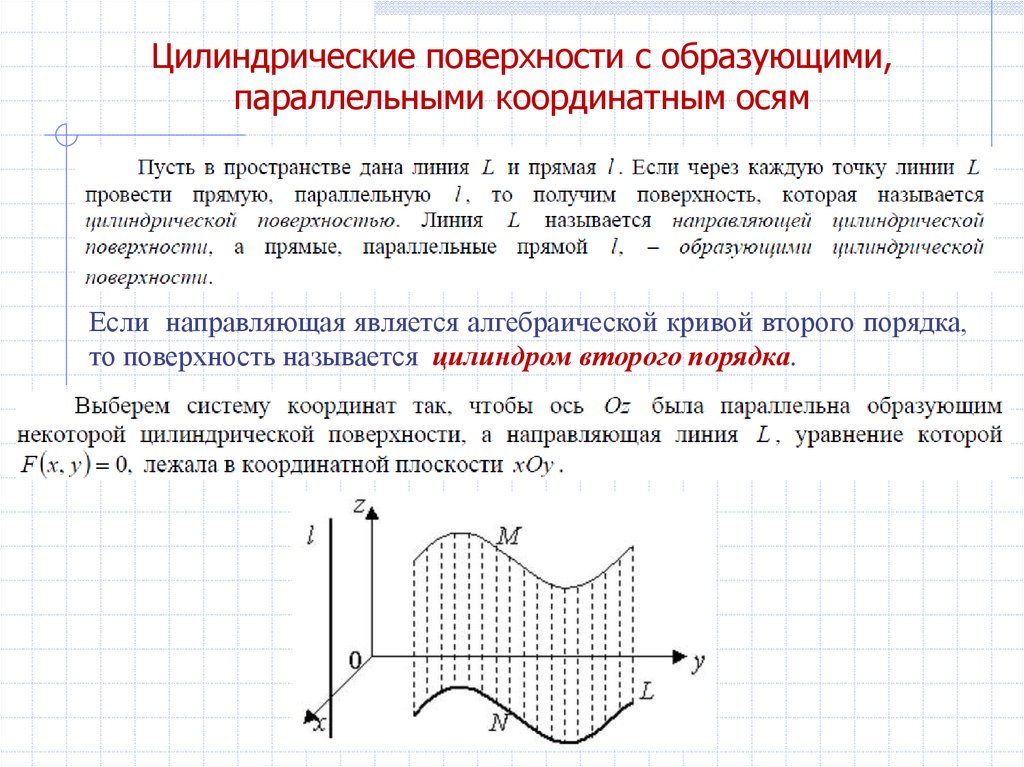
Цилиндрической поверхностью (цилиндром) называется
поверхность, которую описывает прямая (называемая
образующей), перемещающаяся параллельно самой себе
вдоль некоторой кривой (называемой направляющей) .
Цилиндры называют по виду направляющей: круговые,
эллиптические, параболические, гиперболические.

24. Цилиндрические поверхности с образующими, параллельными координатным осям

Если направляющая является алгебраической кривой второго порядка,
то поверхность называется цилиндром второго порядка.

25. Цилиндрические поверхности с образующими, параллельными координатным осям

Правило
Для построения поверхности F(x,y)=0 сначала рисуем линию L с таким же
уравнением на плоскости XOY, затем переносим ее параллельно оси OZ.

26.

Цилиндрические поверхности с образующими,
параллельными координатным осям
Уравнение
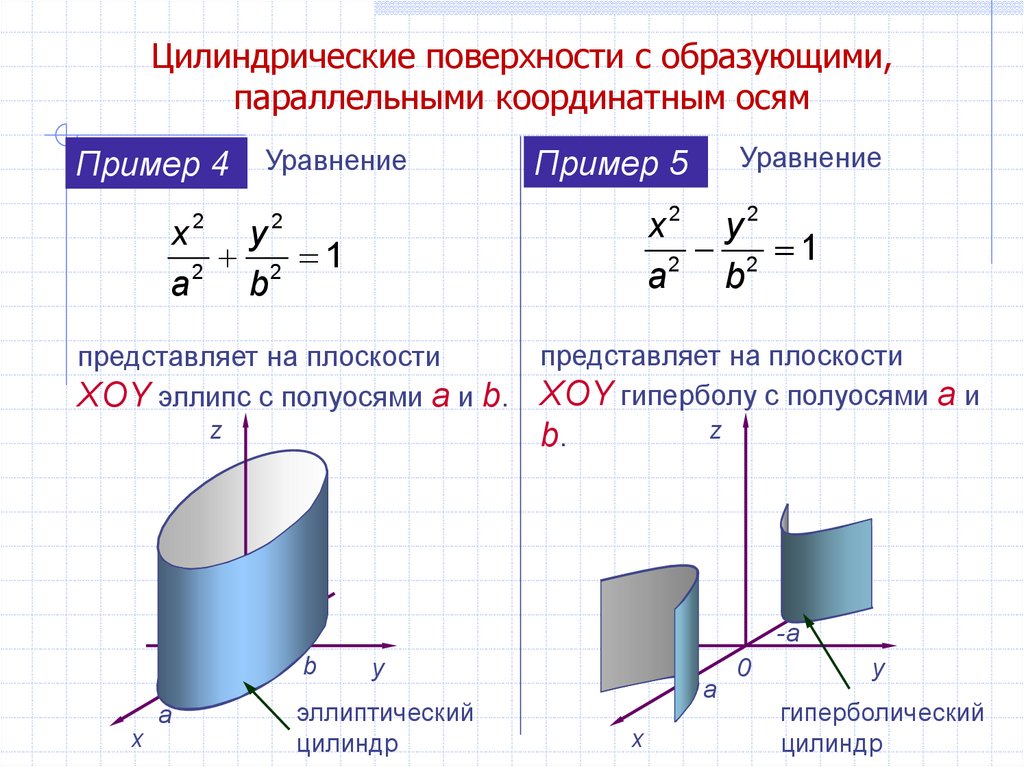
Пример 4
2
Уравнение
Пример 5
x2 y 2
2 1
2
a
b
2
x
y
2 1
2
a
b
представляет на плоскости
XOY эллипс с полуосями а и b.
z
представляет на плоскости
XOY гиперболу с полуосями а и
z
b.
-a
0
a
x
b
y
эллиптический
цилиндр
a
x
0
y
гиперболический
цилиндр

27.

Цилиндрические поверхности с образующими,
параллельными координатным осям
F ( x; z ) 0; F ( y ; z ) 0
Эти уравнения представляют собой цилиндрические поверхности у
которых образующие параллельны осям OY и OX.
Для построения первой поверхности рисуем линию на плоскости
XOZ, затем переносим ее параллельно оси OY , для построения
второй поверхности рисуем линию на плоскости YOZ, затем
переносим ее параллельно оси OX .
z
Пример 6
Уравнение
y 2 2pz
параболический
цилиндр
представляет на
плоскости YOZ
параболу.
0
x
y

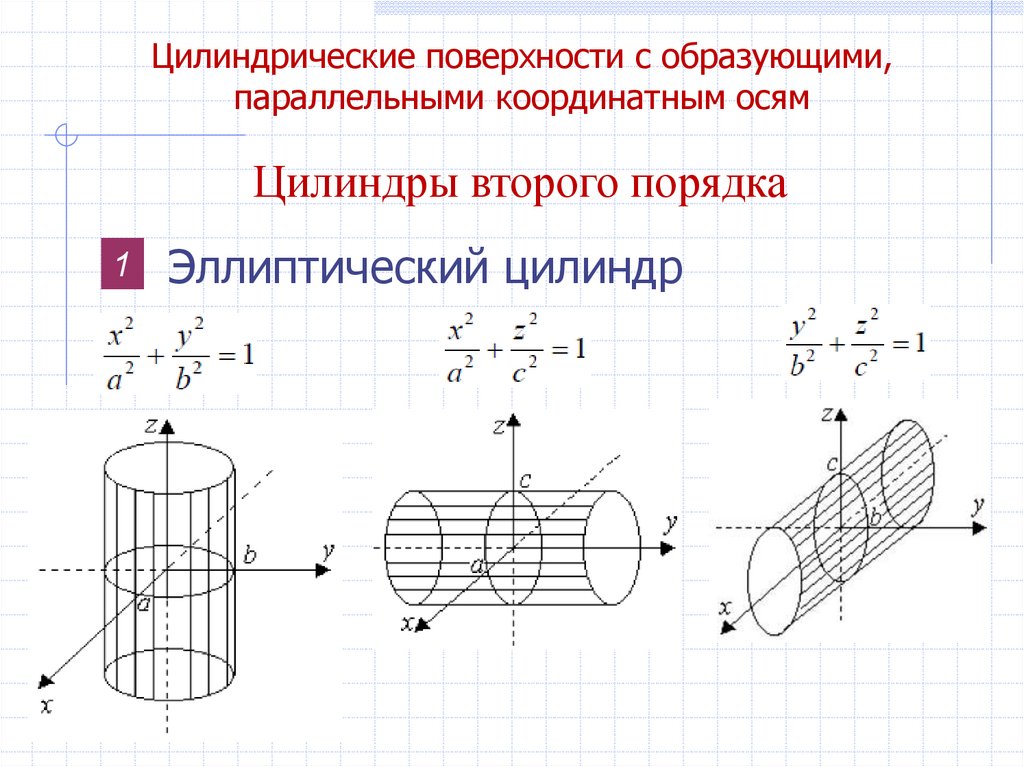
28. Цилиндрические поверхности с образующими, параллельными координатным осям

Цилиндры второго порядка
1
Эллиптический цилиндр

29. Цилиндрические поверхности с образующими, параллельными координатным осям

2
Гиперболический цилиндр
z
0
x
y

30. Цилиндрические поверхности с образующими, параллельными координатным осям

3
Параболический цилиндр