Similar presentations:
Модуль числа. (6 класс)
1. Модуль числа
Урок № 692.
№ 571) Діляться на 2: 252, 160, 210, 336, 520, 890.
2) Діляться на 5: 125, 305, 160, 210, 520, 890.
3) Діляться на 10: 160, 210, 520, 890.
4) Діляться і на 2, і на 5: 160, 210, 520, 890.
3.
360 : 15 + 5 · (500 – 34 · 12) = 4843
6
3
0
0
1
5
2
4
×
3
4
1
2
6
8
6
0
6
0
3
4
0
4
0
5
0
0
– 4
0
8
=
5
·
9
2
=
4
6
0
4
6
4
+
2
4
=
4
9
2
8
4
8
4.
5.
DС
- 12,9
-5
Cім
А В
0 1
Жодного
01
x
2 2,5
x
6.
x- 4- 3- 2 - 10
1
2 3 4
7. Назвати число протилежне даному:
7–7
–4
4
–(–5)
–(+3)
–5
3
-(-6)
-6
–(–2)
–2
–(+9)
9
–(–(–8))
8
8.
Назвіть три числа, які є цілими, але неє натуральними?
Укажіть координату точки, яка
віддалена від початку відліку на 20
одиничних відрізків.
СКІЛЬКИ РОЗВ’ЯЗКІВ МАЄ ЗАДАЧА?
1
1
1
Які з чисел 3; -5,8; 4,7;
; ; 0; 2
2
3
2
1005; -99
можуть виражати відстань від початку відліку
до точки координатної прямої?
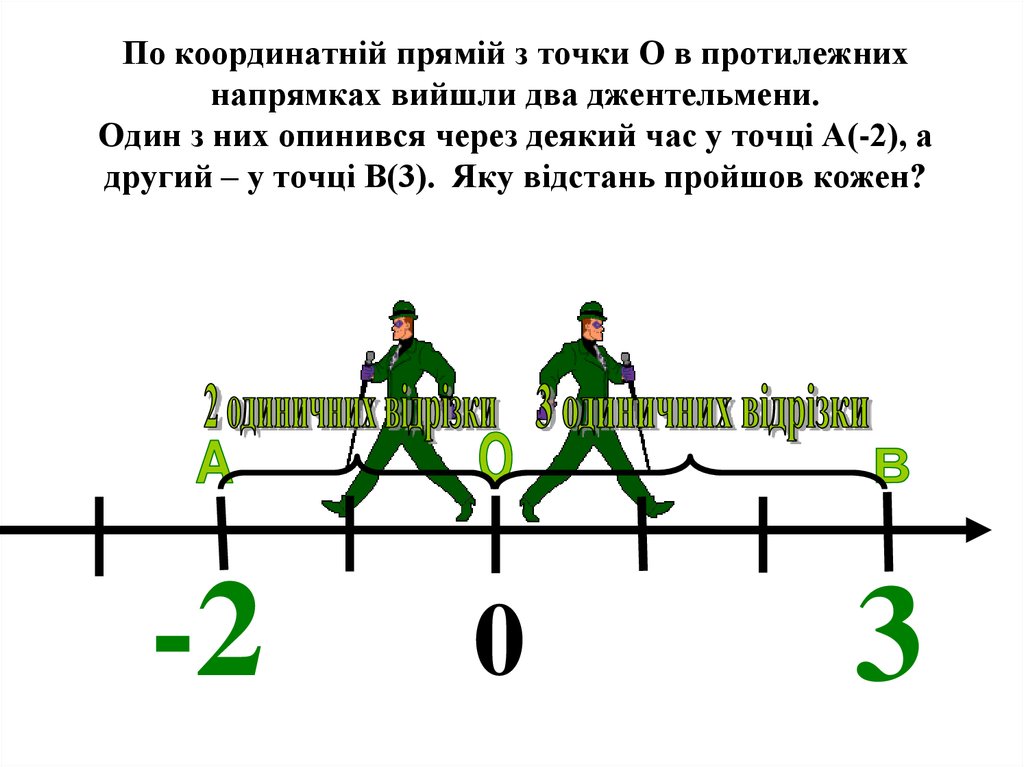
9. По координатній прямій з точки О в протилежних напрямках вийшли два джентельмени. Один з них опинився через деякий час у точці А(-2), а другий
– у точці В(3). Яку відстань пройшов кожен?-2
0
3
10.
–3| –3 | = 3
–4
5
0
|5|=5
0
| –4 | = 4
– 3,5
0
| –3,5 | = 3,5
6
|6|=6
10
| 10 | = 10
|0|= 0
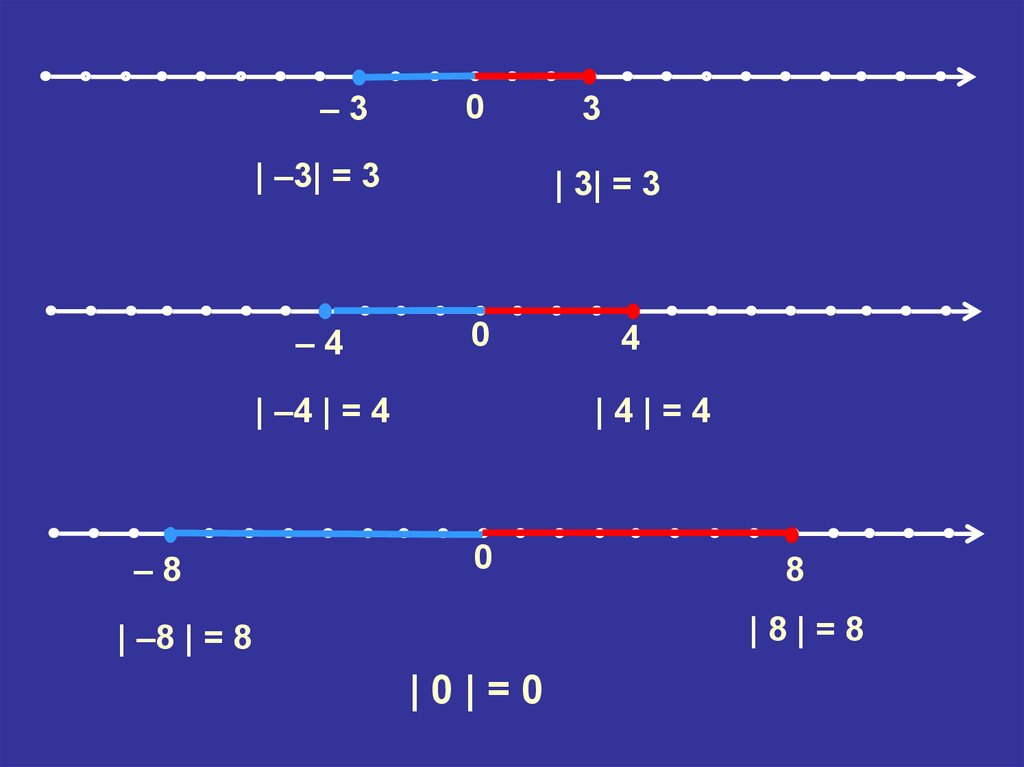
11.
–30
| –3| = 3
–4
| 3| = 3
0
| –4 | = 4
–8
3
4
|4|=4
0
8
|8|=8
| –8 | = 8
|0|=0
12.
–а0
|–а|=а
а
|а|=а
| –а|=|а|
• модуль числа не може бути від’ємним;
• модулі протилежних чисел рівні.
13. Означення модуля
a14.
15.
x 3x = 3 або х=- 3
–3
0
3
16.
x 0х=0
0
17.
x 3Немає коренів!!!
0
18.
x 2-2
0
-2<x<2
2
19.
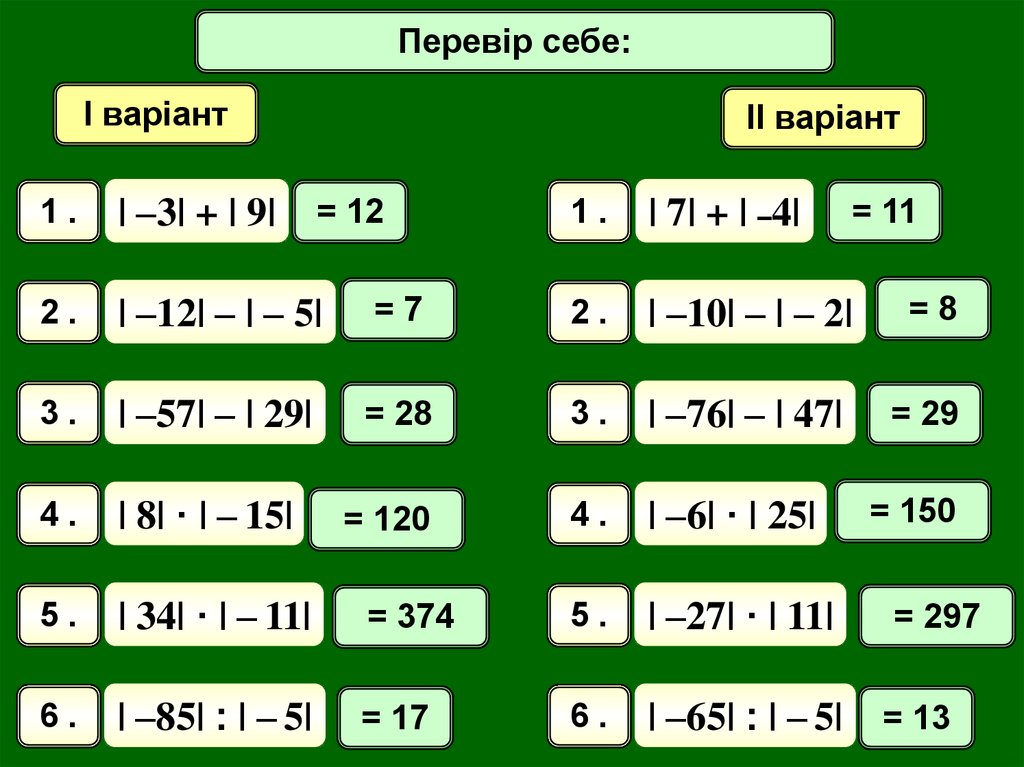
СамостійнаПеревір себе:
робота
І варіант
ІІ варіант
1.
| –3| + | 9|
2.
| –12| – | – 5|
3.
| –57| – | 29|
4.
| 8| · | – 15|
5.
| 34| · | – 11|
6.
| –85| : | – 5|
1.
| 7| + | –4|
=7
2.
| –10| – | – 2|
=8
= 28
3.
| –76| – | 47|
= 29
= 120
4.
| –6| · | 25|
= 374
5.
| –27| · | 11|
= 17
6.
| –65| : | – 5| = 13
= 12
= 11
= 150
= 297
20. Підсумок уроку.
Швидко відповідаємо на запитання: на дошцізаписане число 9
• Яке це число?
• Його модуль?
• Йому протилежне?
• Йому обернене?
• Де розташоване на координатній прямій?
• Відстань від початку відліку?
• Відстань між ним і йому протилежним?
• Число, що має менший модуль?
• Розв’язком якого рівняння може бути?
21.
Домашнє завданняЧитати § 23
№ 1005, 1011, 1025
Повторити § 3 № 98, № 1113(1)











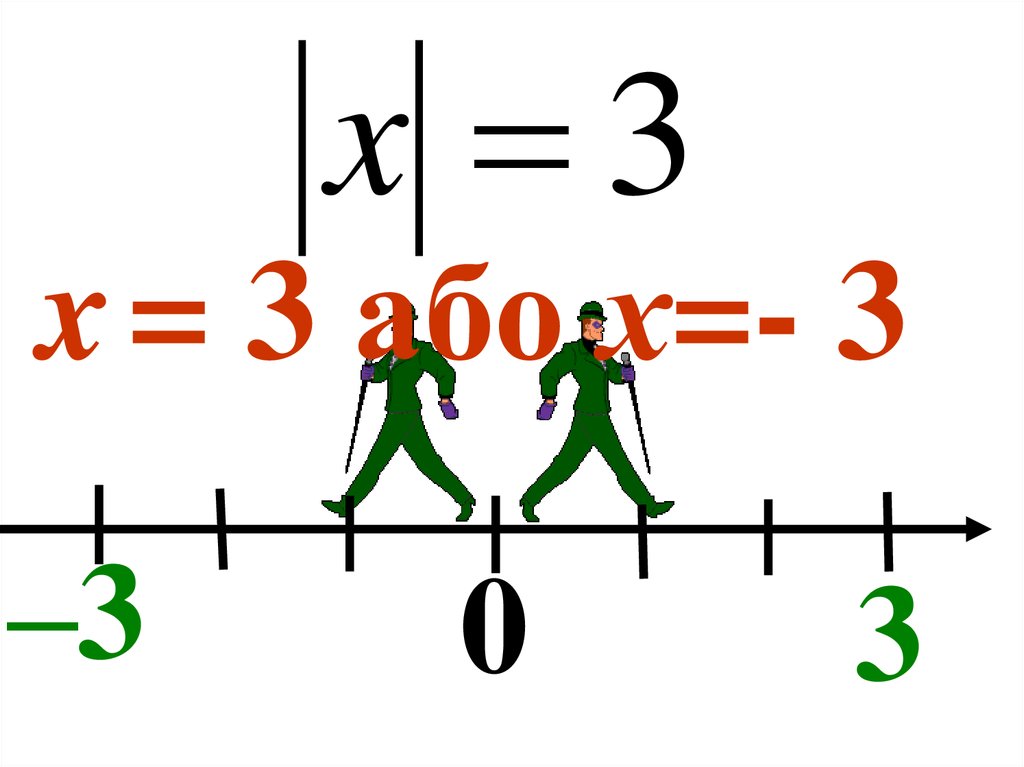

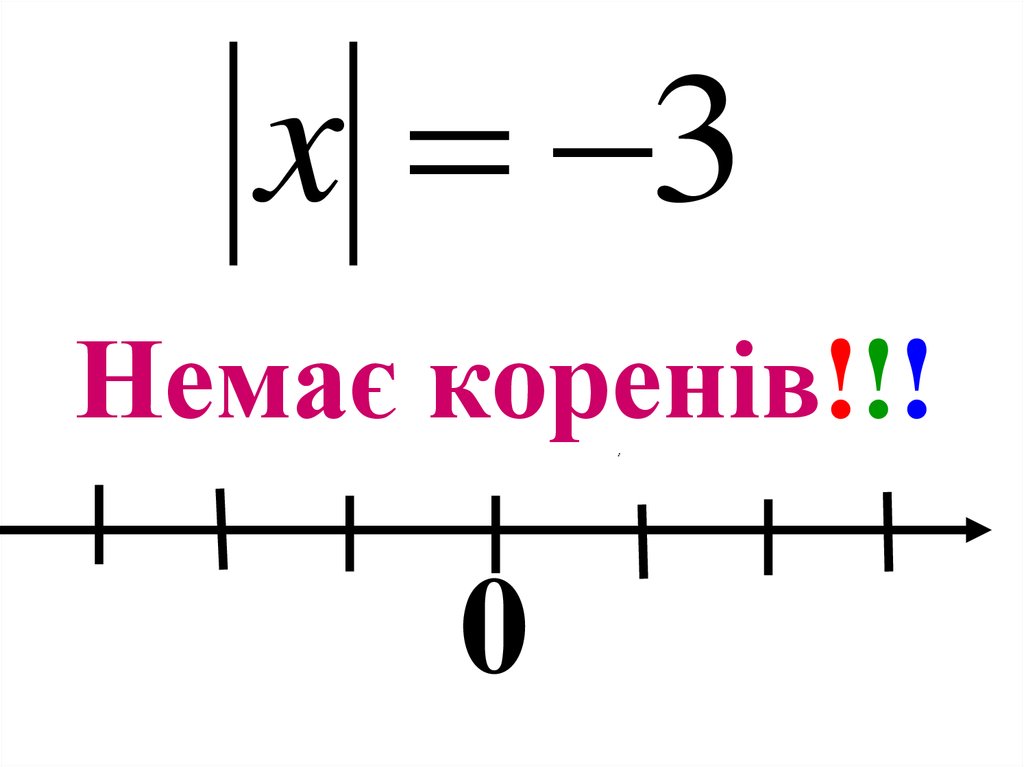



 mathematics
mathematics








