Similar presentations:
Планирование производственно- хозяйственной деятельности
1. ПЛАНИРОВАНИЕ ПРОИЗВОДСТВЕННО-ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ
МЭИ каф. ЭКОПЛАНИРОВАНИЕ
ПРОИЗВОДСТВЕННОХОЗЯЙСТВЕННОЙ
ДЕЯТЕЛЬНОСТИ
2.
МЭИ каф. ЭКОПланирование
–
это
разработка
и
установление
руководством
предприятия
системы
количественных
и
качественных
показателей его развития, определяющих темпы,
пропорции и тенденции развития данного
предприятия как в текущем периоде, так и на
перспективу.
3. Принципы планирования
МЭИ каф. ЭКОПринципы планирования
Принцип единства
Принцип участия
Принцип непрерывности
Принцип гибкости
Принцип точности
4. Методы планирования
МЭИ каф. ЭКОМетоды планирования
Балансовый
Расчетно-аналитический
Экономико-математическое моделирование
Графоаналитический
Программно-целевой
5. Задачи планирования
МЭИ каф. ЭКОЗадачи планирования
1. Планирование объемов выпуска продукции в
течение планового периода
2. Планирование путей развития производства
3. Обоснование производственной программы
Разработка балансов производственных мощностей
Выбор
оптимального варианта производственной
программы
Определение потребности в ресурсах
Разработка мероприятий по повышению качества
продукции
Расчет
технико-экономических
показателей
производства
6. Оптимизация режимов работы электростанций
МЭИ каф. ЭКООптимизация режимов
работы электростанций
7.
МЭИ каф. ЭКООдной из важнейших задач
эксплуатации является экономичное
распределение энергетической нагрузки
между электростанциями энергосистемы
и отдельными их блоками и агрегатами.
При таком распределении обеспечивается
минимальный расход энергоресурсов на
выработку требуемого количества энергии.
8. Экономико-математическая модель задачи оптимизации
МЭИ каф. ЭКОЭкономико-математическая модель
задачи оптимизации
1. Целевая функция
n
E E1 E 2 ... E n Ei min
i 1
2. Уравнение ограничений
• балансовое
n
W W1 W2 ... Wn Wi
i 1
в виде неравенств
Wi min Wi Wi max
9. Метод относительных приростов
МЭИ каф. ЭКОМетод относительных приростов
Для обеспечения минимального расхода
тепла и топлива, нагрузка работающих
агрегатов должна быть такой, чтобы величина
удельного прироста расхода тепла этих
агрегатов была одинакова.
Еn
Е1
Е2
r1;
r2 ;...;
rn
W1
W2
Wn
r1 r2 ... rn r
10. Виды энергетических характеристик
МЭИ каф. ЭКОВиды энергетических характеристик
• Расходные (абсолютные)
• Относительные
• Дифференциальные
11.
МЭИ каф. ЭКОАбсолютные
(расходные)
характеристики
показывают взаимосвязь между первичной и
вторичной энергией. К ним относятся зависимости:
• расхода топлива электростанции от ее мощности
Вст = f (Pст)
• расхода топлива котлом от его
теплопроизводительности
Вк = f (Qч)
• расход тепла турбин в зависимости от ее
электрической мощности
Qч = f (Pт)
12.
МЭИ каф. ЭКООтносительные характеристики используются для
расчета первичной энергии от нагрузки. К ним
относятся
зависимости
удельных
расходов
топлива, теплоты и КПД от нагрузки:
bуд = f (Pст); ηст = f (Pст).
Удельные расходы характеризуют экономичность
работы:
• для котла, тут/ГДж
bк Вч / Qк
• для турбин, (ГДж/ч)/МВт
qк Qт / Рт
• для блока или электростанции, тут/МВт
bуд Вч / Р
13.
МЭИ каф. ЭКОДифференциальные
характеристики
используются
для
определения
оптимальных режимов работы агрегатов;
т.е. нахождения условий, при которых
расход
топлива,
теплоты
или
себестоимости
энергии
будет
минимальным при условии соблюдения
графика нагрузки.
∂ Вст
∆ Вст
= f (Pст)
= f (Pст).
∂ Рст
∆ Рст
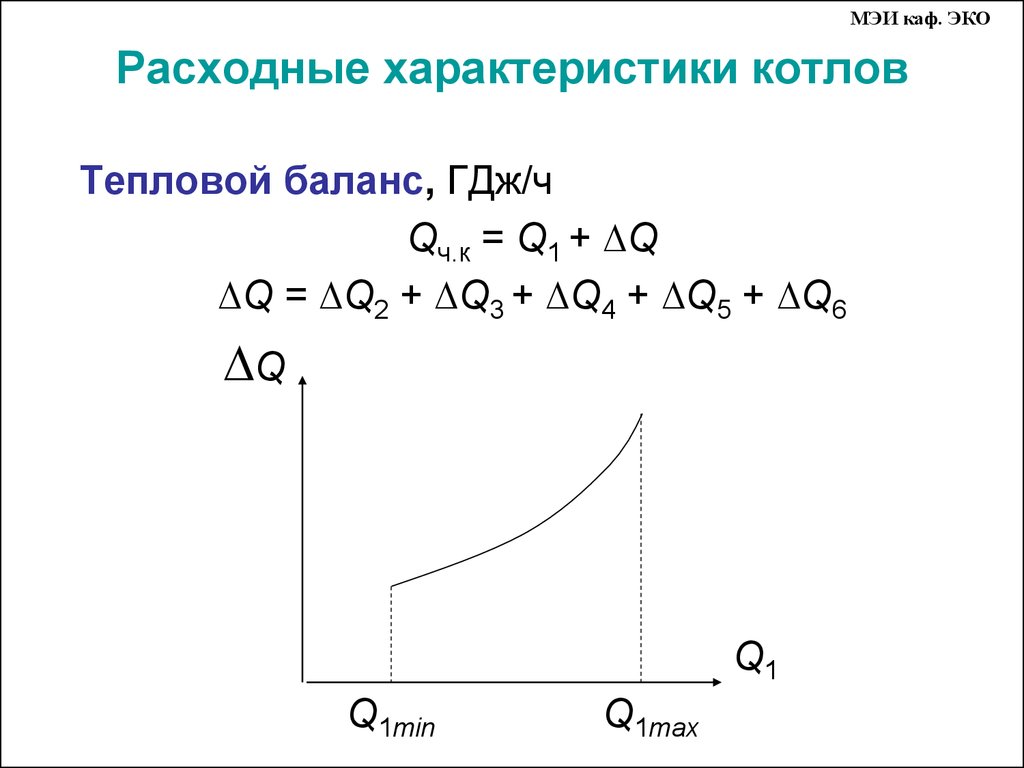
14. Расходные характеристики котлов
МЭИ каф. ЭКОРасходные характеристики котлов
Тепловой баланс, ГДж/ч
Qч.к = Q1 + ∆Q
∆Q = ∆Q2 + ∆Q3 + ∆Q4 + ∆Q5 + ∆Q6
∆Q
Q1
Q1min
Q1mах
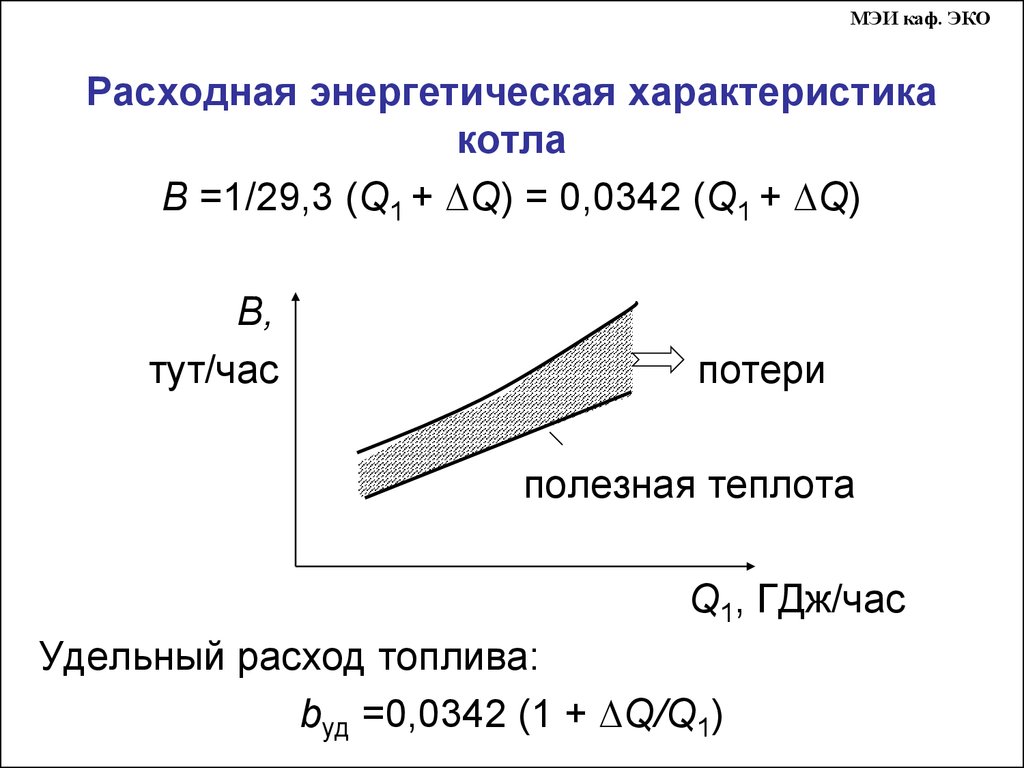
15.
МЭИ каф. ЭКОРасходная энергетическая характеристика
котла
В =1/29,3 (Q1 + ∆Q) = 0,0342 (Q1 + ∆Q)
В,
тут/час
потери
полезная теплота
Q1, ГДж/час
Удельный расход топлива:
bуд =0,0342 (1 + ∆Q/Q1)
16.
МЭИ каф. ЭКОДифферециальная характеристика котла
d ∆Q
dB
rк =
= 0,0342 (1 +
dQ1
)
dQ1
17.
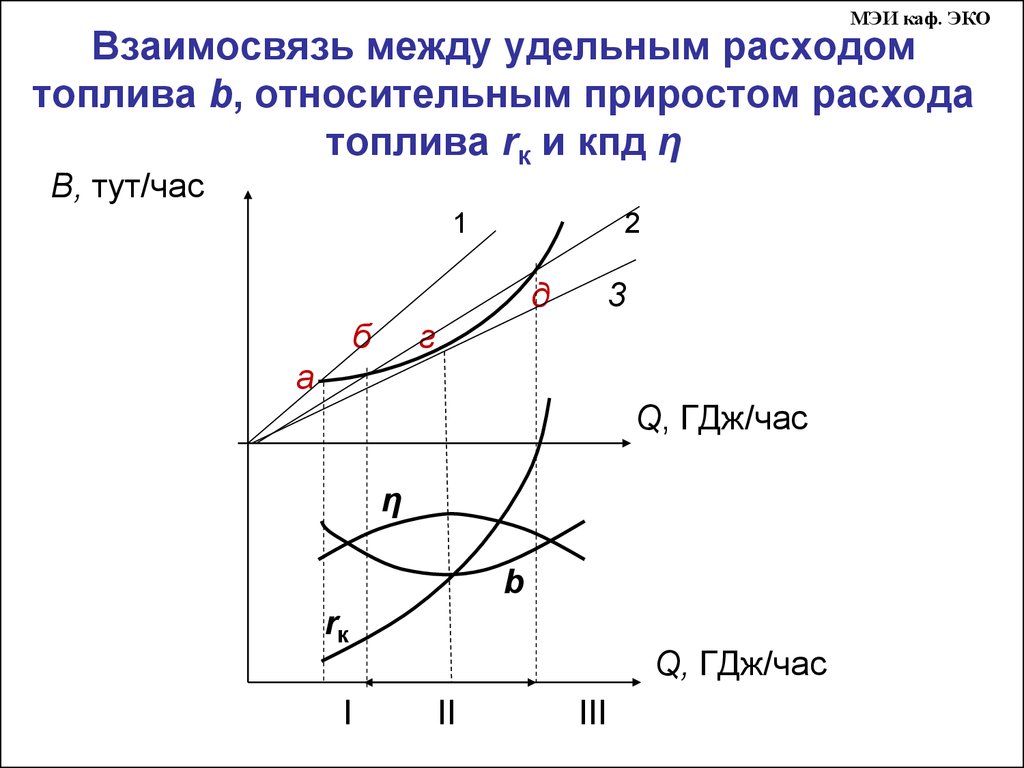
МЭИ каф. ЭКОВзаимосвязь между удельным расходом
топлива b, относительным приростом расхода
топлива rк и кпд η
В, тут/час
1
2
д
б
3
г
а
Q, ГДж/час
η
b
rк
I
Q, ГДж/час
II
III
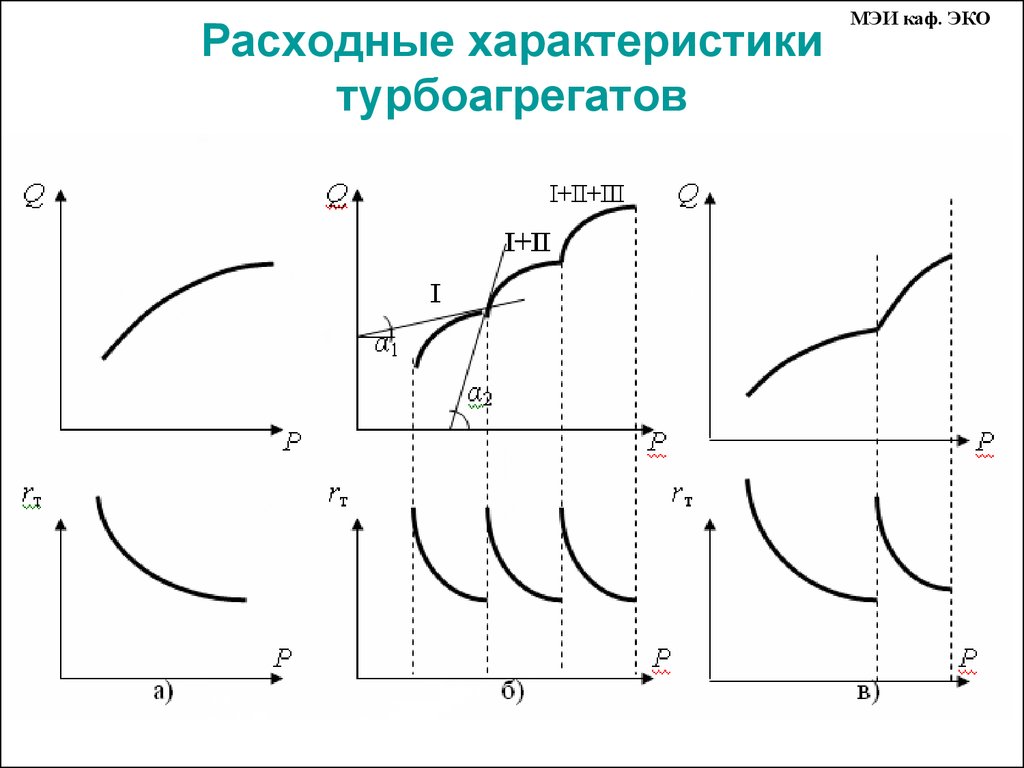
18. Расходные характеристики турбоагрегатов
МЭИ каф. ЭКО19.
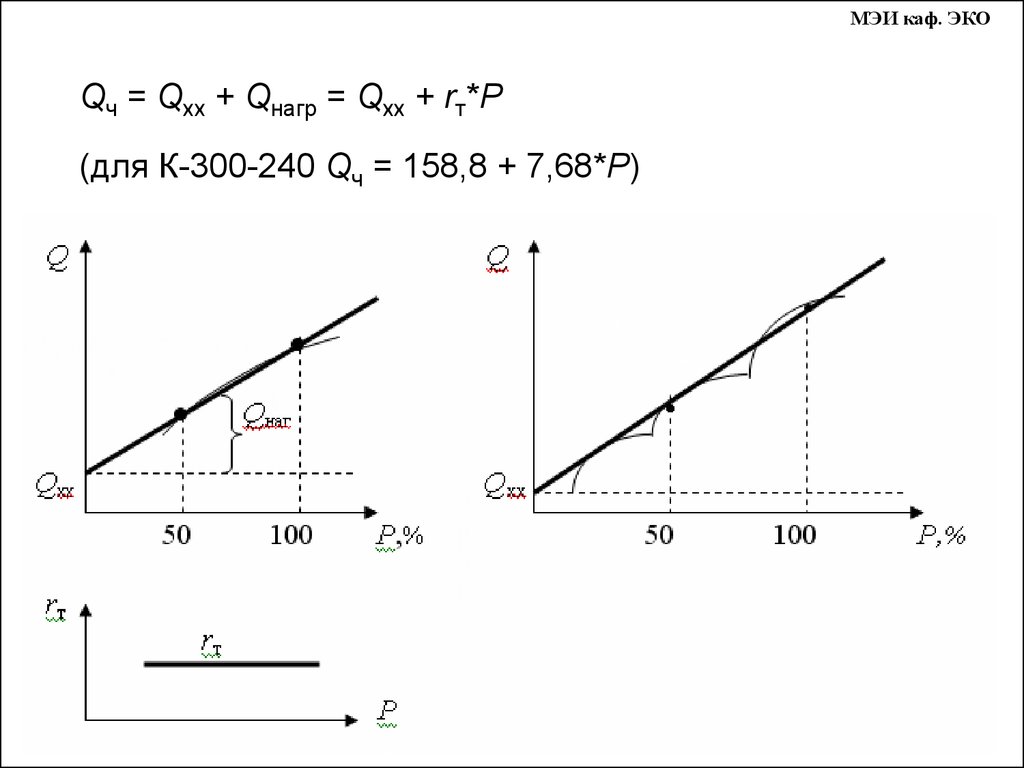
МЭИ каф. ЭКОQч = Qхх + Qнагр = Qхх + rт*Р
(для К-300-240 Qч = 158,8 + 7,68*Р)
20.
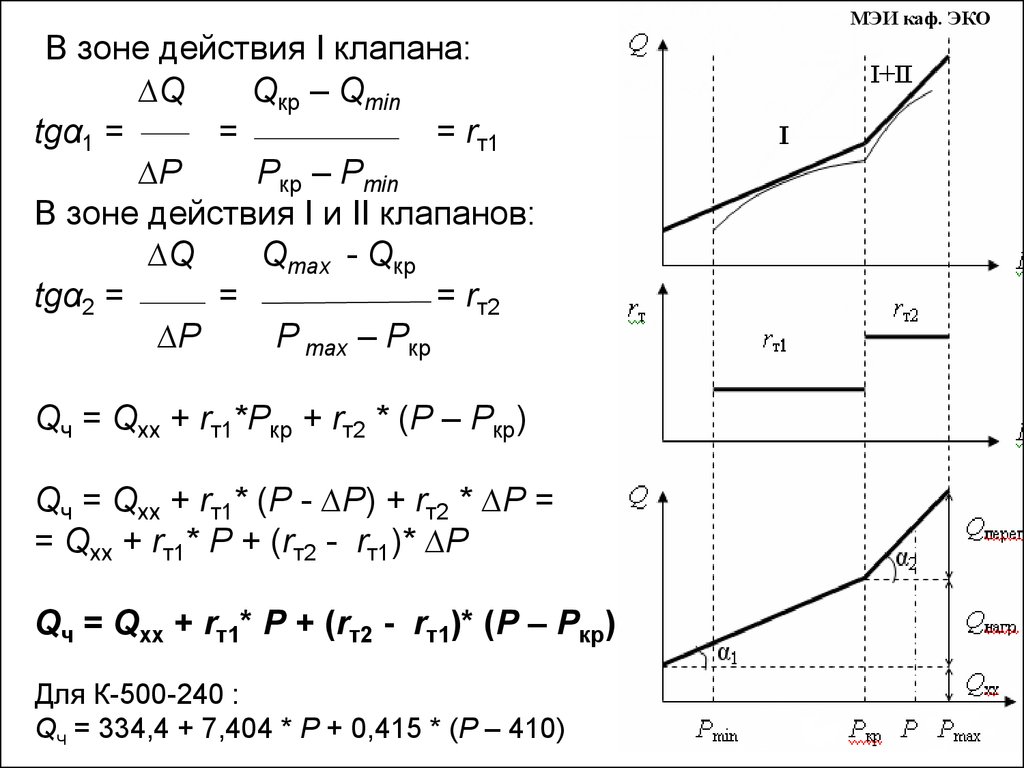
В зоне действия I клапана:∆Q
Qкр – Qmin
tgα1 =
=
= rт1
∆P
Ркр – Рmin
В зоне действия I и II клапанов:
∆Q
Qmах - Qкр
tgα2 =
=
= rт2
∆P
Р mах – Ркр
Qч = Qхх + rт1*Ркр + rт2 * (Р – Ркр)
Qч = Qхх + rт1* (Р - ∆Р) + rт2 * ∆Р =
= Qхх + rт1* Р + (rт2 - rт1)* ∆Р
Qч = Qхх + rт1* Р + (rт2 - rт1)* (Р – Ркр)
Для К-500-240 :
Qч = 334,4 + 7,404 * Р + 0,415 * (Р – 410)
МЭИ каф. ЭКО
21.
МЭИ каф. ЭКОРасходные характеристики ТЭЦ
Qч = Qхх+ δт ∆т + δп∆п + (βт + δ′т ∆т) Dт +
+ (βп + δ′п ∆п) Dп +
n
j
rт1 Р + ( rтj 1 – rт )(Р – Ркр i)
j 1
Qч = Qхх + βтDт + βпDп +
1
rт Р
+
n
( rтj 1 – rтj
j 1
)(Р – Ркр i)
ПТ-80-130/565:
Qч = 62,7 + 1,72 Dп + 0,557 Dт + 8,82 Р +1,08 (Р – Ркр1)
22.
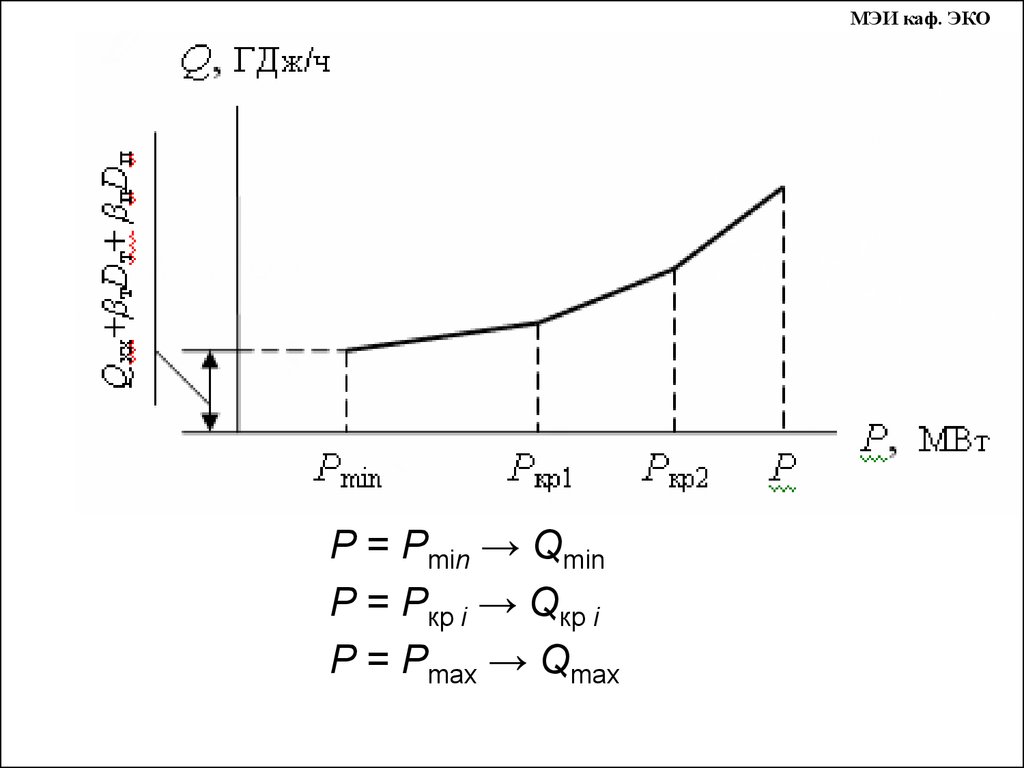
МЭИ каф. ЭКОР = Рmin → Qmin
Р = Ркр i → Qкр i
Р = Рmах → Qmах
23.
МЭИ каф. ЭКО24.
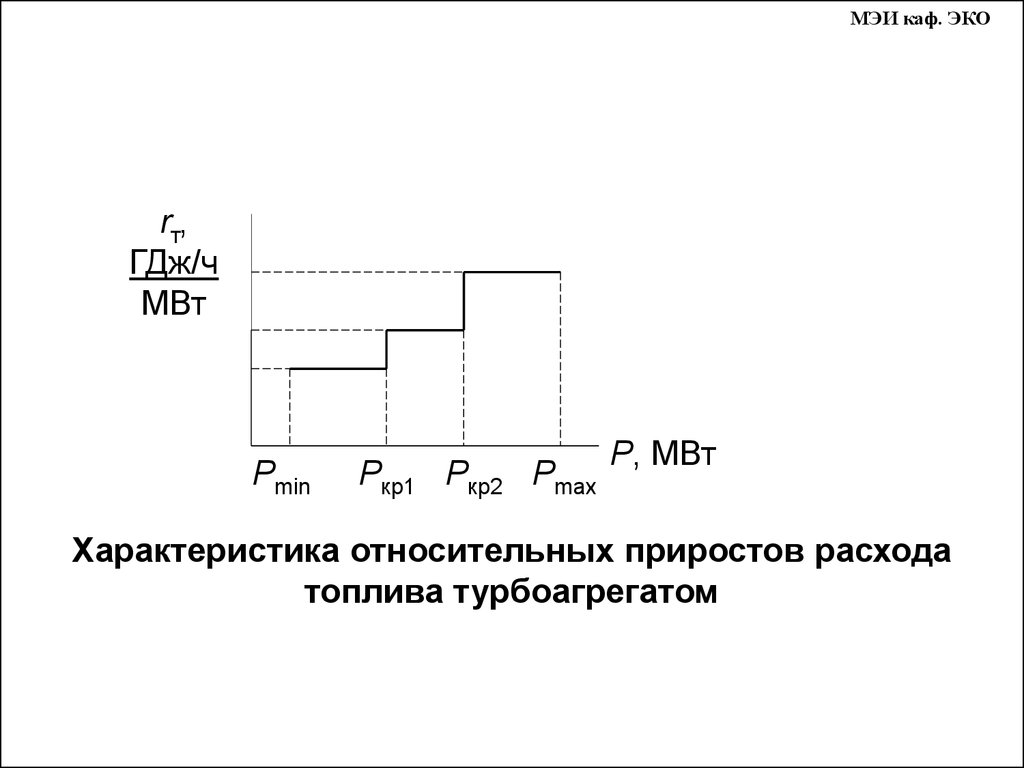
МЭИ каф. ЭКОrт,
ГДж/ч
МВт
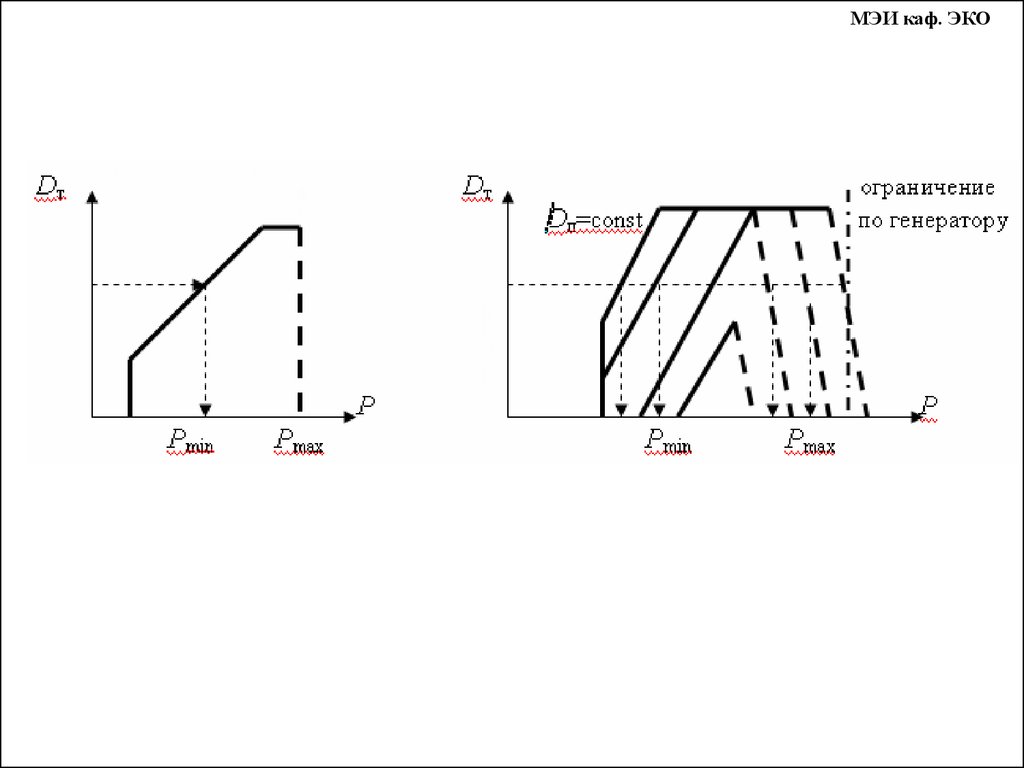
Рmin
Ркр1 Ркр2 Рmax
Р, МВт
Характеристика относительных приростов расхода
топлива турбоагрегатом
25. Методы оптимального распределения нагрузки между котлами в котельной
МЭИ каф. ЭКОМетоды оптимального
распределения нагрузки
между котлами в
котельной
26. rк1 = rк2 = rк3 = …= rкi = … = rкn rк1 Ц1 = rк2 Ц2= rк3 Ц3= …= rкm Цm= … = rкn Цn
МЭИ каф. ЭКОrк1 = rк2 = rк3 = …= rкi = … = rкn
rк1 Ц1 = rк2 Ц2= rк3 Ц3= …= rкm Цm= … = rкn Цn
Цm
Цn
Ц1
Ц2
rк1
rк 2
... rкm
... rкn
Цб
Цб
Цб
Цб
27.
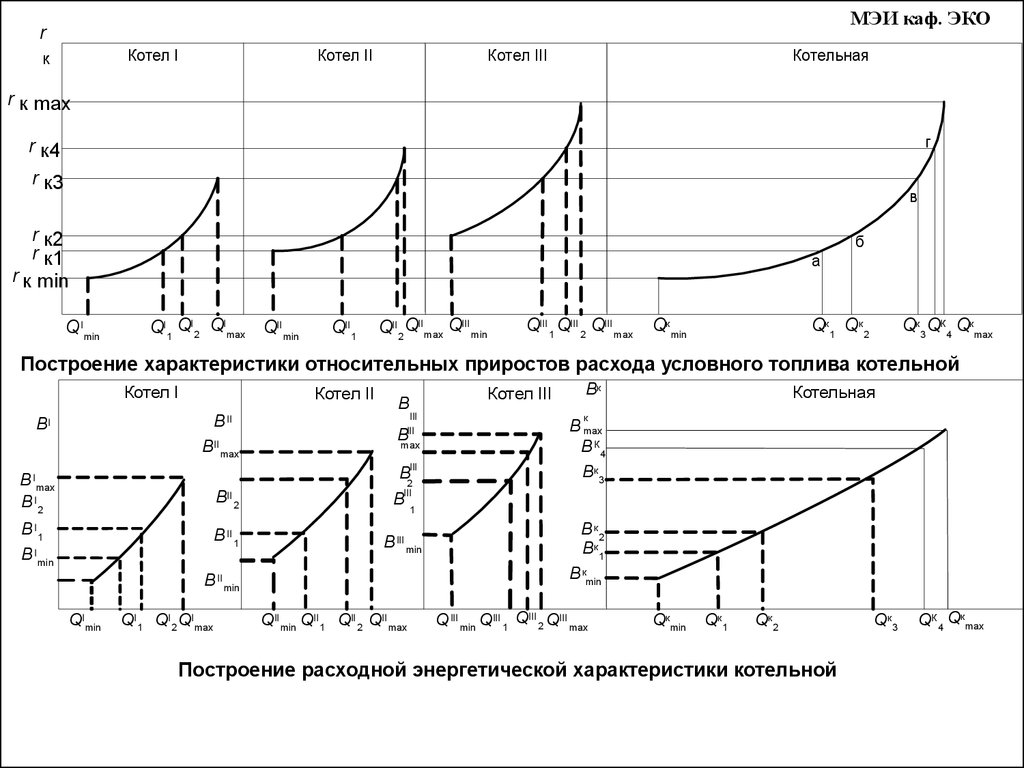
МЭИ каф. ЭКОr
Котел I
к
Котел II
Котел III
Котельная
r к max
г
r к4
r к3
в
r к2
r к1
б
а
r к min
QImin
QI1 QI 2 QImax
QII min
QII 1
QII 2 QII max QIII min
QIII 1 QIII 2 QIII max
Qкmin
Qк1 Qк 2
Qк3 QК 4 Qкmax
Построение характеристики относительных приростов расхода условного топлива котельной
Котел I
Котел II
В II
ВI
ВII max
Котел III
В
III
III
max
В
В2III
В I max
В I2
ВII 2
ВIII
В I1
В I min
В II 1
В III min
QI 1 QI 2 QI max
Котельная
к
В max
В К4
Вк 3
1
В к2
Вк 1
В кmin
В II min
QI min
Вк
QII min QII 1 QII 2 QII max
Q III min QIII 1 QIII 2 QIII max
Qк min
Qк 1
Qк2
Построение расходной энергетической характеристики котельной
Qк 3
QК 4 Qк max
28.
МЭИ каф. ЭКОк
I
II
III
Qmin
Qmin
Qmin
Qmin
к
Q1
I
Q1
к
Q2
I
Q2
II
Qmin
II
Q1
III
Qmin
III
Qmin
к
I
II
III
Bmin
Bmin
Bmin
Bmin
к
B1
к
B2
I
B1
I
B2
II
Bmin
II
B1
III
Bmin
III
Bmin
29. Методы оптимального распределения нагрузки между турбоагрегатами теплоэлектростанции
МЭИ каф. ЭКОМетоды оптимального
распределения нагрузки
между турбоагрегатами
теплоэлектростанции
30.
МЭИ каф. ЭКО1
1
r
Q1 = Qхх1 + т1Р + ( rт12 – rт1
)(Р – Ркр)
1
т2Р
Q2 = Qхх2 + r
2
т2
+( r
1
r
– т2 )(Р – Ркр)
31.
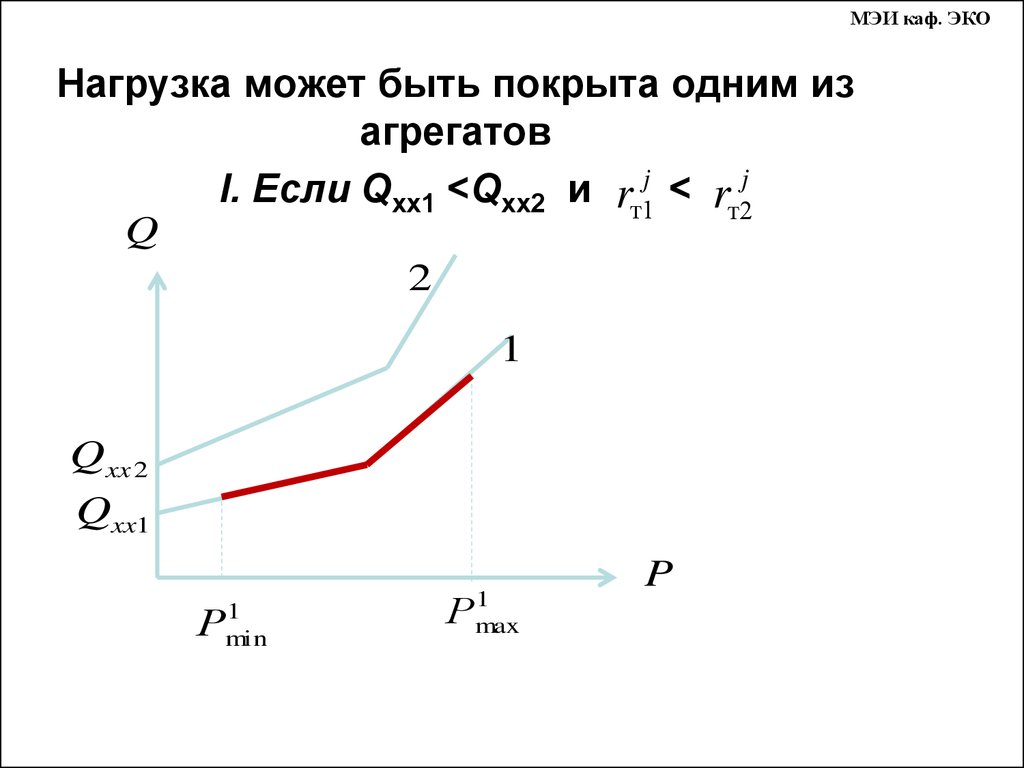
МЭИ каф. ЭКОНагрузка может быть покрыта одним из
агрегатов
I. Если Qхх1 <Qхх2 и rт1j < rт2j
Q
2
1
Qxx 2
Qxx1
Р
1
min
1
Рmax
P
32.
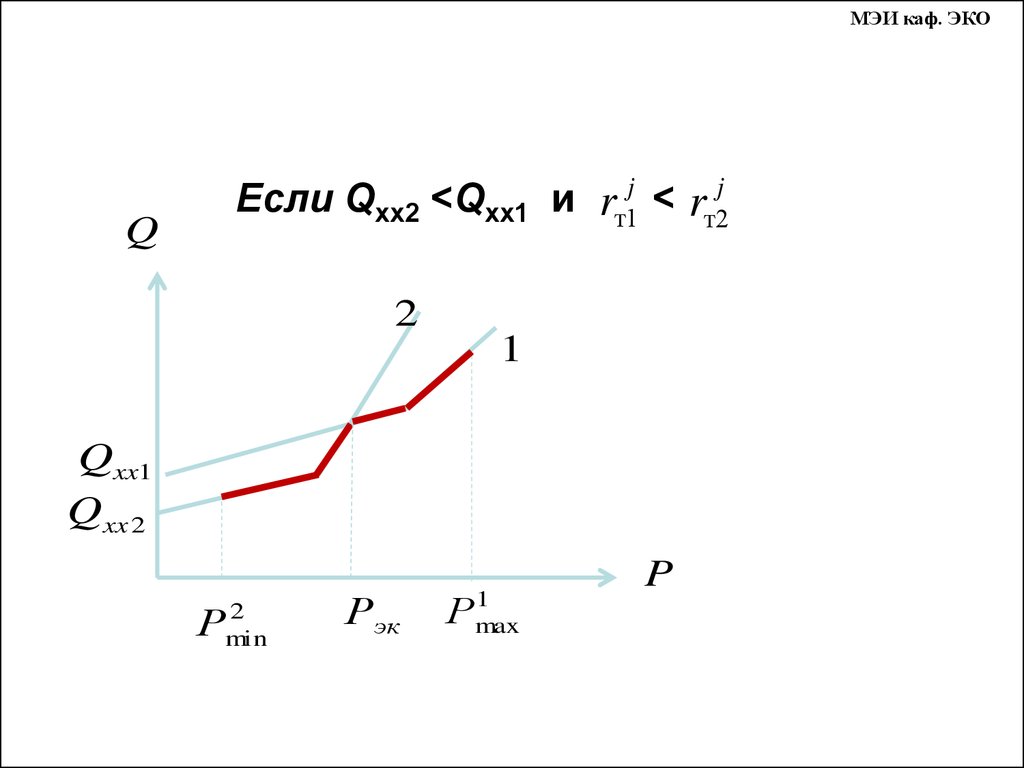
МЭИ каф. ЭКОЕсли Qхх2 <Qхх1 и rт1j < rт2j
Q
2
1
Qxx1
Qxx 2
Р
2
min
Рэк
1
Рmax
P
33.
МЭИ каф. ЭКОQ
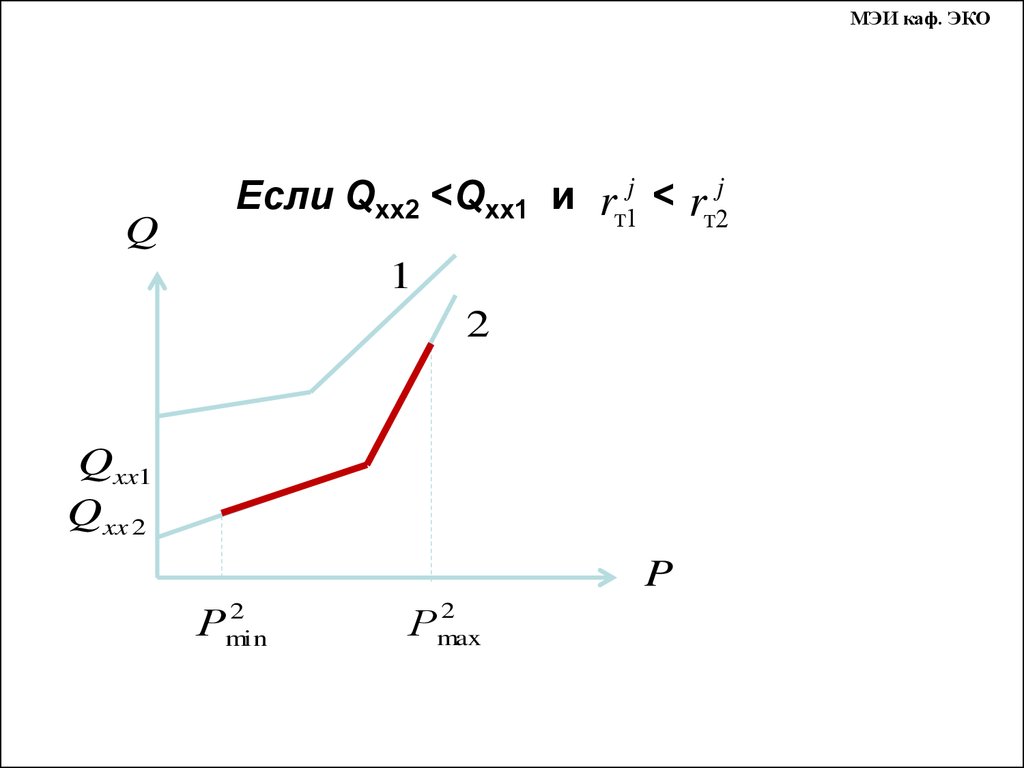
Если Qхх2 <Qхх1 и rт1j < rт2j
1
2
Qxx1
Qxx 2
P
2
Рmin
2
Рmax
34.
МЭИ каф. ЭКО.
rт1 rт 2 ... rтn
rт1 rт 2 ... rтn
















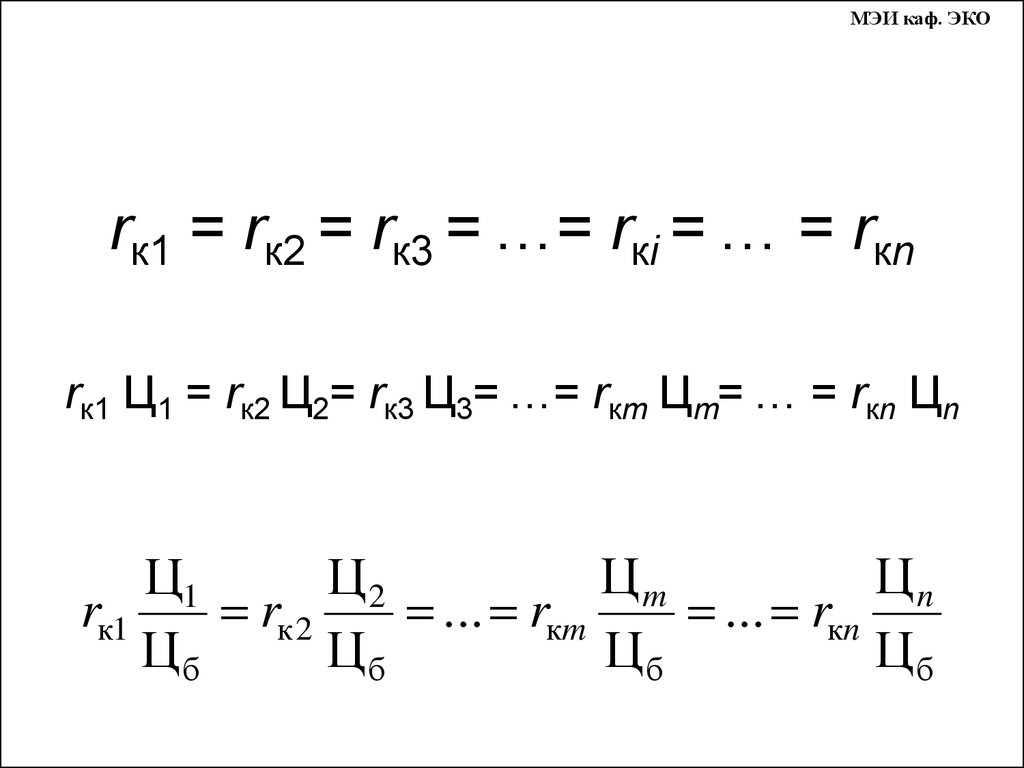


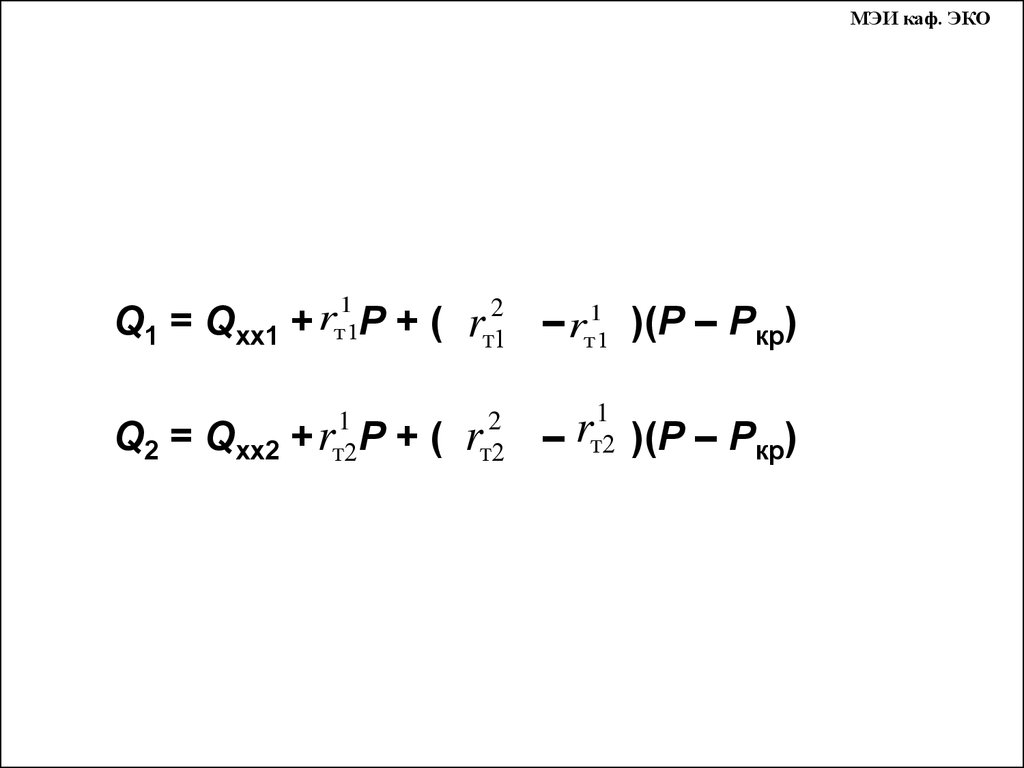
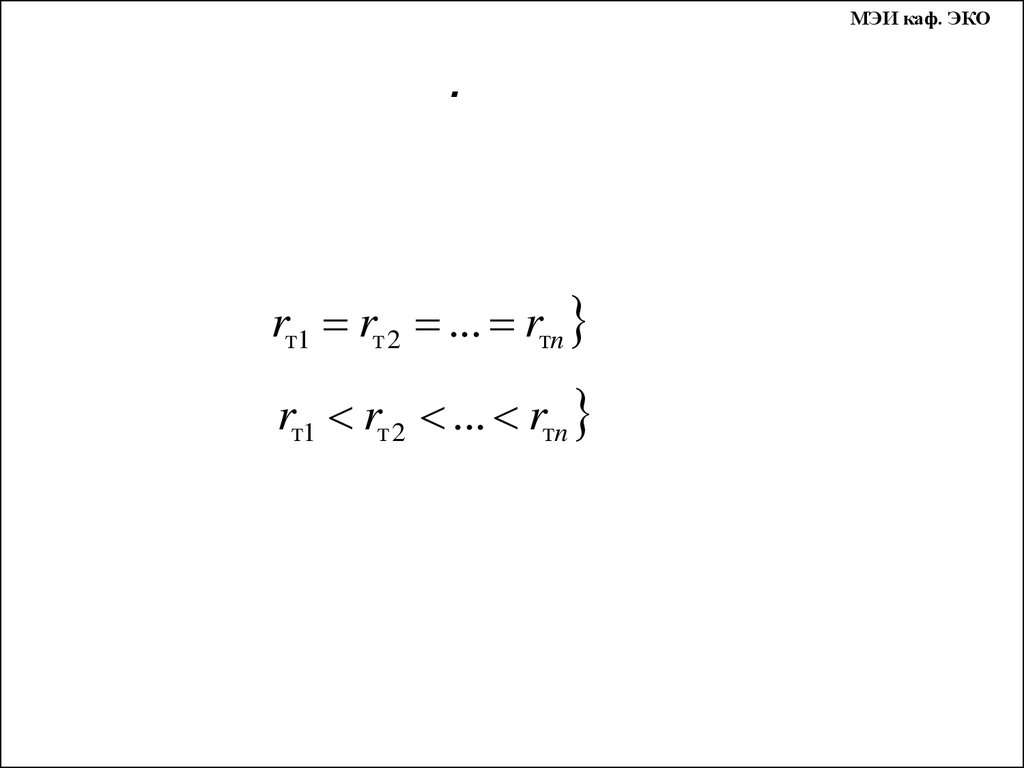
 management
management industry
industry








