Выбор оптимальной надежности объектов наземной космической инфраструктуры

1. Выбор оптимальной надежности объектов наземной космической инфраструктуры

2. Общая постановка задачи оптимизации надежности

Общая задача выбора оптимальной надежности объекта НКИ и путей ее обеспечения
может быть сформулирована следующим образом.
Требуется выбрать такие проектные параметры объекта НКИ
N , N з ,Cэ ,Cтр ,Tтр ,Tпр , Nи ,
при которых суммарные затраты минимизируются, т. е.
С С P,PN ,Cод ,Cодз ,Cотк min
при выполнении дисциплинирующих условий, связывающих стоимость и надежность
с проектными параметрами
Сод Сод N , Nз ,Cэ ,Cтр ,Tтр ,Tпр , Nи , Nпр , К ;
Р N ,N з ,Cэ ,Cтр ,Tтр ,Tпр ,Nи ,Nпр ,

3.

и ограничений по массе и габаритам
Gдоп G N , Nз ,Cэ ,Cтр ;
Lдоп L N , Nз ,Cэ ,Cтр .
Требуется определить оптимальную надежность агрегата, если стоимость приобретения
агрегата определяется по формуле:
К2
Спр К 1 1 .
Поскольку время отказов имеет экспоненциальное распределение, то вероятность
безотказной работы за время Т будет:
Р е Т
причем среднее время между отказами:
Т ср
1

4.

а среднее число отказов за время Т:
nср T
Полезное время работы агрегата за время Т будет:
Т п.в.р T nсрТ вос Т 1 Т вос
Суммарные затраты на один час работы агрегата будут:
С
Спр С1эТ
Т 1 Т вос
Подставив вместо Спр ( ) его значение будем иметь:
К 1 С1эТ К 1К 2
С1
Т 1 Т вос
Для выбора оптимальной надежности (вероятности безотказной работы) необходимо
найти такое , которое обращает функцию затрат С1 в минимум, а затем полученное
значение opt подставить в формулу (5.67).

5.

Взяв производную
С1
и приравняв ее нулю, найдем оптимальное значение:
opt
К1К 2
К1 С1эТ
1
1
К1 С1эТ
Т вос К1К 2
Подставляя значение орt из (24.4) в (5.67), получаем оптимальное значение
вероятности безотказной работы агрегата:
Popt exp optT

6. Определение оптимального режима тренировок

Если обозначить через t интенсивность отказов элемента после тренировки, то
средняя интенсивность отказов в течение времени t будет:
T тр t
ср
t dt
T тр
t
ср
Для определения минимальной ср приравняем производную t к нулю:
1
Т тр t Т тр 0
t
Количество не отказавших за время тренировок элементов должно быть равно N
элементам, используемым в объекте НКИ:
Tтр
Nотр Ne
t dt
0
где Nотр — количество элементов, поставленных на тренировку.

7.

Tтр t
После тренировки не откажет Ne
t dt
Tтр
элементов, а откажет соответственно
T t
N 1 exp t dt
T
тр
Nотк
тр
Определим суммарные затраты, которые включают в себя:
а) стоимость элементов, поставленных на тренировку:
T
Сэ1N exp t dt
0
тр
Сэ1N отр
б) стоимость тренировки:
Стр N отр Т тр Стр N Т тр
T
exp t dt
0
тр
в) ущерб от отказа элементов:
T t
Сэ 2N 1 exp t dt
T
тр
Сэ 2Nотк
тр

8. Определение оптимального времени замены элементов

Затраты, связанные с профилактической заменой элемента, равны C п .з , а
затраты при отказе элемента во время работы Cо. р , то средняя стоимость замены
элементов за время Т Т зм будет:
Сср nо.рСо.р nп.зCп.з
где nо. р , и nп . з — число отказавшихся во время работы и замененных в
профилактических целях элементов. Соответственно эти величины определяются по
формулам:
nо. р n 1 P Т зм
nп .з nP Т зм
где n — среднее число замененных элементов
n
Т
Т змср

9.

Подставив
nо.р , nп .з и nв выражение для средних затрат, будем иметь:
Т
Сср ср Со. р 1 Р Т зм Сп.з Р Т п.з
Т зм
Задача определения оптимального времени замены элементов КСНО сводится к
выбору такого Т зм , при котором удельные средние затраты Сср , определяемые по
формуле (5.88), минимальны.
Следует отметить, что для экспоненциального распределения времени службы
элементов их профилактическая замена целесообразна, поскольку функция Сср Сср Т зм
монотонно убывает и не имеет минимума

10. Выбор оптимального распределения надежности отдельных элементов НКИ.

Вероятность безотказной работы объекта НКИ при отсутствии резервирования
может быть определена по формуле (для случая малых значений)
P Pi 1 qi 1 qi
Отсюда
N
N
N
i 1
i 1
i 1
N
q1 1 P q i
i 1
Суммарная стоимость объекта НКИ складывается из стоимостей отдельных
элементов:
N
Ai
A1 N Ai
A1
Ai
С Сi
N
q1 i 2 q i
i 1
i 1 q i
i 2 qi
1 P qi
N
N
i
1
i
i
i 2
Следует выбрать вероятность отказа i-го элемента q i таким образом, чтобы
суммарная стоимость объекта НКИ была минимальной.

11.

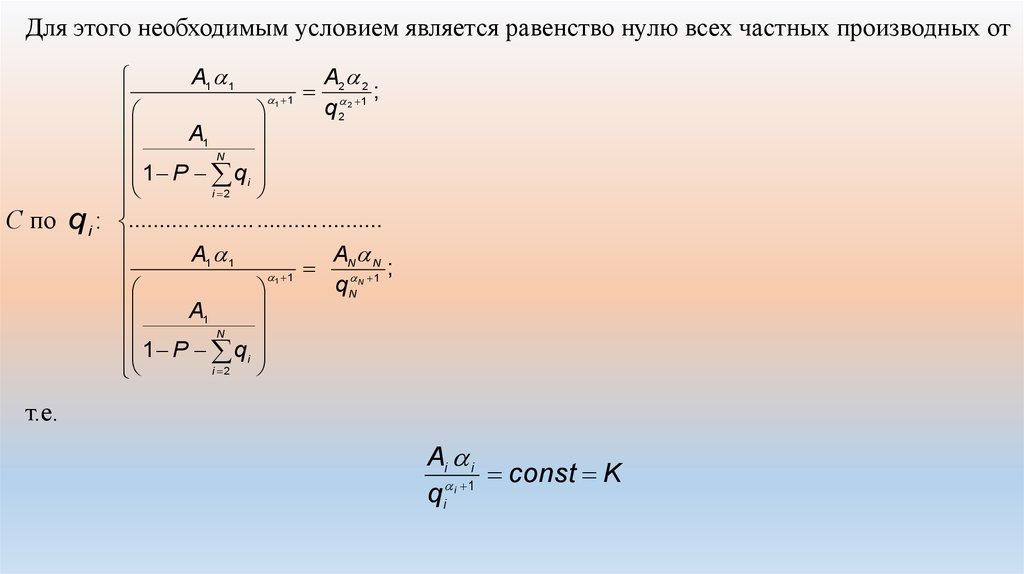
Для этого необходимым условием является равенство нулю всех частных производных от
A1 1
A2 2
;
1
1
q2
A
1
N
1 P q
i
i 2
С по q i : .......... .......... .......... ..........
A1 1
AN N
;
1
1
qN
A1
N
1 P q i
i 2
1
1
2
N
т.е.
Ai i
const K
1
qi
i

12.

Из (24.26) имеем
Ai i
qi
K
1
i 1
Подставив q i вычисленное по формуле (24.27), в формулу (24.22), будем иметь:
Ai i
P 1
K
i 1
N
1
i 1
Откуда при i const можно определить
N A 1 1
i
i
i 1
K
1
P
i
i 1

13.

Выражение (24.27) с учетом (24.29) можно записать
q i 1 P
A
A
i
i
1
i 1
N
i 1
i
i
1
i 1
Полученная зависимость дает возможность найти оптимальное распределение
надежности отдельных элементов при заданной надежности всего НКИ (или агрегата
НКИ), а также совместно с уравнением (24.24) позволяет найти зависимость P f C при
оптимальном распределении надежности отдельных элементов. Имея зависимость P f C
и пользуясь методикой для выбора оптимальной надежности объекта НКИ или его
агрегатов, изложенной выше, можно определить оптимальную надежность всего НКИ.

14. Определение оптимального числа резервных элементов НКИ

Если надежность всей НКИ задана, то при наличии резервирования вероятность
безотказной работы будет:
P 1 qini
N
i 1
Определение оптимального числа резервных элементов n i заключается в выборе такого
вектора N (с компонентами n i), который минимизирует суммарную стоимость НКИ.
Суммарная стоимость НКИ может быть представлена следующей зависимостью:
C C0 Ci a 1g i a 2 l i3 ni
N
i 1
При определении оптимального количества резервных элементов следует учитывать
возможность существования ограничений по массе и габаритам, которые для данного
случая могут быть представлены в следующем виде:
N
Gдоп i ni
i 1
где i 1gi 2l i3 , i 2 l i3
Lдоп
N
i 1
i
ni

15.

Оптимизацию будем проводить методом неопределенных множителей Лагранжа, для чего
составим функцию
N
F x i ni 1 q in P
i 1
i 1
N
i
и, приравняв производные по n i и к нулю, получим
x i q in ln q i
N
q in
P 1
i 1
0;
i
i
0.
Решение этой системы уравнений позволяет найти оптимальное значение
где bi
xi
ln q i
1 P bi
ln N
bi
n i i 1
ln q i