Similar presentations:
Производная сложной функции
1.
Пусть переменная y есть функция от переменнойu, y=f(u).
И пусть переменная
переменной x, u=φ(x).
u
есть
То есть задана сложная функция
y f (x )
функция
от
2.
Если y=f(u), u=φ(x) – дифференцируемыефункции своих аргументов, то производная
сложной функции существует и равна
производной
данной
функции
по
промежуточному аргументу, умноженной на
производную
самого
промежуточного
аргумента по независимой переменной:
y f (u ) u x
3.
Дадим аргументу х приращение Δх, не равное 0,тогда функции u=φ(x), y=f(u) получат приращения
Δu и Δy.
Предположим, что Δu не равно нулю, тогда в
силу дифференцируемости функции y=f(u)
получим:
y
lim
f (u )
u 0
u
Причем, величина
f (u )
не зависит от Δu.
4.
На основании теоремы о связи бесконечно малыхвеличин с пределами функций функцию, стоящую
под знаком предела, можно представить как
сумму этого предела и бесконечно малой
величины:
y
f (u ) ( u )
u
где α(Δu) – бесконечно малая величина при u 0
Отсюда:
y f (u ) u ( u ) u
Делим обе части равенства на Δx:
y
u
u
f (u )
( u )
x
x
x
5.
Т.к.по
условию
функция
u=φ(x)
дифференцируема, то она непрерывна в точке x.
Следовательно, при
и u 0
x 0
( u ) 0
Переходим в последнем равенстве к пределу при
x 0
y
u
u
y lim
lim
f (u ) lim ( u ) lim
x 0 x
x 0 x
x 0
x 0 x
f (u ) u x
u x
0
6.
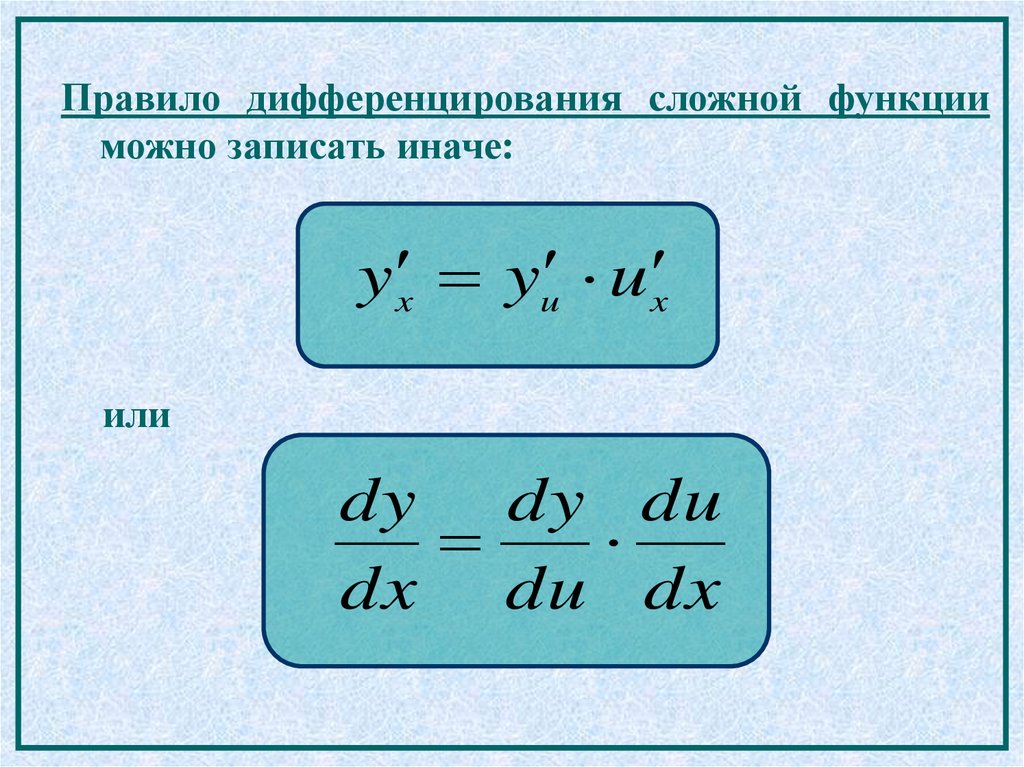
Правило дифференцирования сложной функцииможно записать иначе:
y x yu u x
или
dy dy du
dx du dx
7.
Найти производные сложных функций:1
y
x 5
3
8.
2y 3 x 5 x 5
3
1
x 5 x
2
2
1
2
3
2
1
x 5
x
2
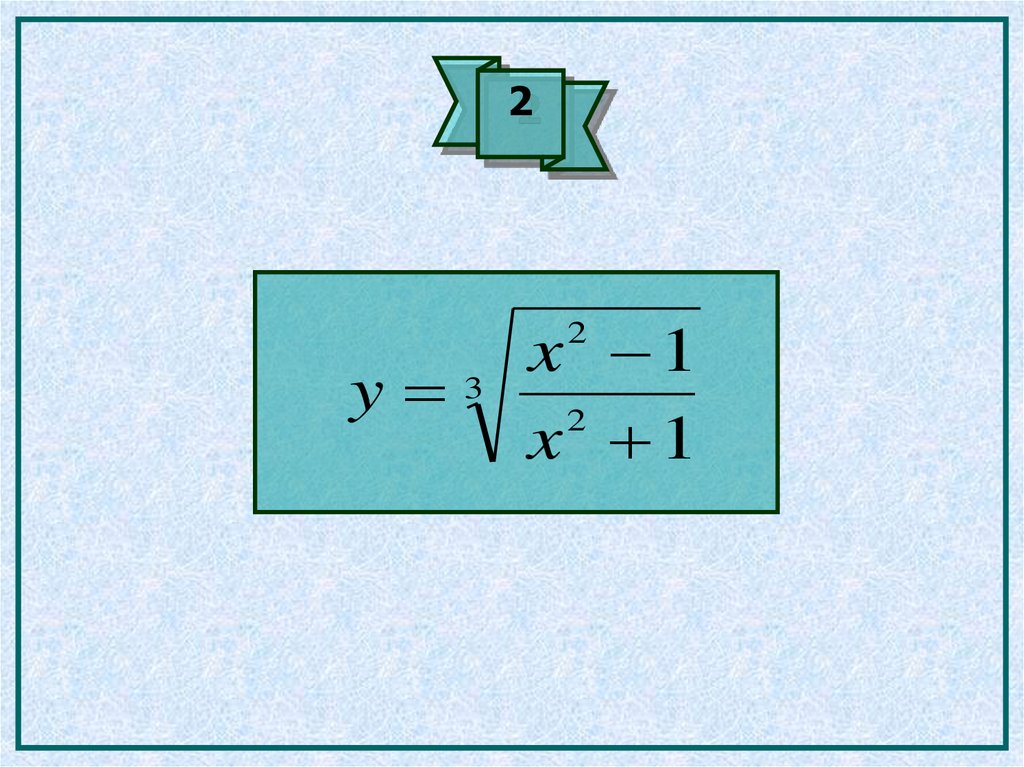
9.
2y 3
x 1
2
x 1
2
10.
1 x 1y 2
3 x 1
2
2
3
2
3
x 1
2
x 1
2
1 x 1 ( x 1) ( x 1) ( x 1) ( x 1)
2
2
2
3 x 1
( x 1)
2
2
2
2
2
11.
23
1 x 1 2 x ( x 1) 2 x ( x 1)
2
2
2
3 x 1
( x 1)
2
1 x2 1
2
3 x 1
2
2
3
2
2 x3 2 x 2 x3 2 x
2
2
( x 1)
2
3
2
1 x 1
4x
2 2
3 x 1 ( x 1) 2








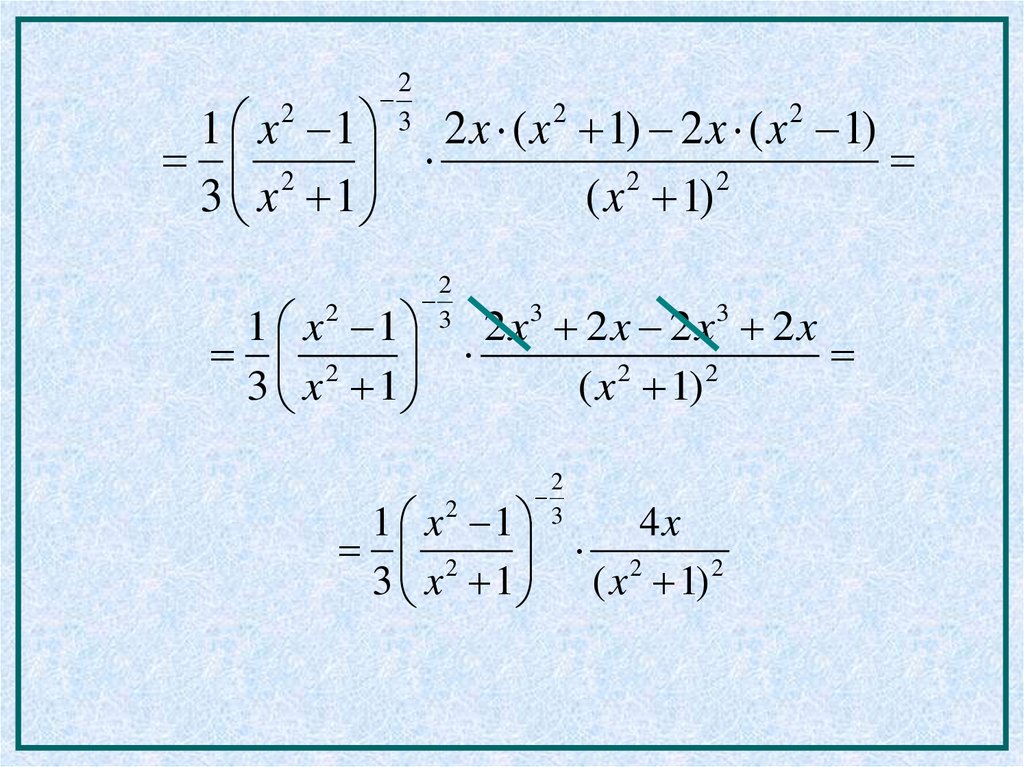
 mathematics
mathematics








