Similar presentations:
Наибольшее и наименьшее значение функции
1.
При нахождении наибольшего и наименьшегозначения функции нескольких переменных,
непрерывной на некотором множестве, следует
иметь в виду, что эти значения достигаются
функцией или в точках экстремума или на
границе множества.
2.
Найти наибольшее и наименьшеезначение функции
1
1
z
2
2
1 x 1 y
на круге с радиусом, равным 1,
с центром в начале координат.
3.
1Найдем частные производные.
z
2x
z x
x
(1 x 2 ) 2
z
2y
z y
2 2
y
(1 y )
4.
2Найдем критические точки.
z
2x
0
2 2
x
(1 x )
z
2y
0
2 2
y
(1 y )
Одна критическая точка (0,0).
x 0
y 0
5.
3Найдем критические точки на границе области.
x y 1
2
2
y 1 x
2
2
1
1
1
1
z
2
2
2
2
1 x 1 1 x
1 x
2 x
2 x2 1 x2
3
3
2
2
2
2
4
(1 x )( 2 x ) 2 2 x x x
2 x2 x4
6.
4x 2x2 x (2 x 1)
z
0
2
4 2
2
4 2
(2 x x )
(2 x x )
3
2
x1 0
1
x2
2
1
x3
2
1
x
2
1
y
2
- критические точки на границе
области.
1
x
2
1
y
2
1
x
2
1
y
2
1
x
2
1
y
2
7.
4Найдем значения
точках.
z (0,0) 2
функции
1 4
1
z
,
2 3
2
1
1 4
z
,
2
2 3
3
z ( 1,0)
2
в
критических
1
1 4
z
,
2
2 3
1 4
1
z
,
2 3
2
3
z 1,0
2
8.
z наиб (0,0) 21
1
1
1
z наим z
,
,
z
2
2
2
2
1
1 4
1
1
z
,
,
z
2
2
2 3
2







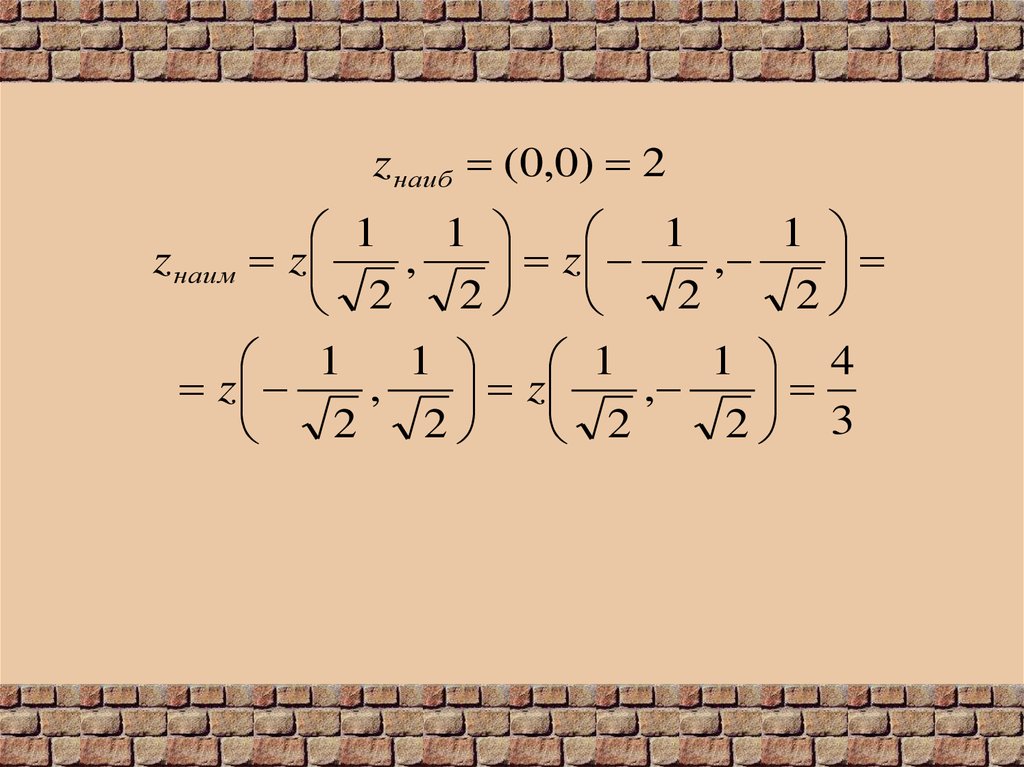
 mathematics
mathematics








