Компланарные векторы. (Урок 5)

1. Компланарные векторы

Урок 5

2. Цели урока

• Ввести определение компланарных векторов.
• Рассмотреть признак компланарности трех
векторов и правило параллелепипеда,
сложение трех некомпланарных векторов.

3. Новый материал

Определение.
Векторы называются компланарными, если при
откладывании от одной и той же точки они будут
лежать в одной плоскости.
Иначе: векторы называются компланарными, если
имеются равные им векторы, лежащие в одной
плоскости.
Любые два вектора компланарны.
Три вектора, среди которых имеются два
коллинеарных, также компланарны.
Почему?
Три произвольных вектора могут быть как
компланарными, так и некомпланарными.

4. Новый материал

Устно: 355
D1
C1
A1
B1
D
A
C
B

5. Новый материал

Признак компланарности трех векторов:
Если вектор с можно представит ь в виде с х а у b ,
где х и у некоторые числа , то векторы a , b и с компланарны .
Дано : а , b , с
а
b
с x a y b .
Доказать : а , b , с компланарны

6. Новый материал

Признак компланарности трех векторов:
Доказатель ство .
а
Пусть a и b неколлинеарны .
Отложим от некоторой точки пространст ва О
b
векторы ОА a и ОВ b .
Векторы ОА и ОВ лежат в плоскости ОАВ.
С Построим векторы х а и у b .
В1
В
Для определенности будем считать
b
О
ОС х а у b
а
А
А1
что х 0 , y 0. ОА1 х а и ОВ1 y b .
Векторы ОА1 и ОВ1 также лежат в плоскости ОАВ.
Их сумма вектор ОС х ОА у ОВ , равный вектору с , лежит
в плоскости ОАВ.

7. Новый материал

Итак , векторы ОА а , ОВ b , ОС c лежат в одной плоскости ,
т . е . векторы а , b , и c компланарны .
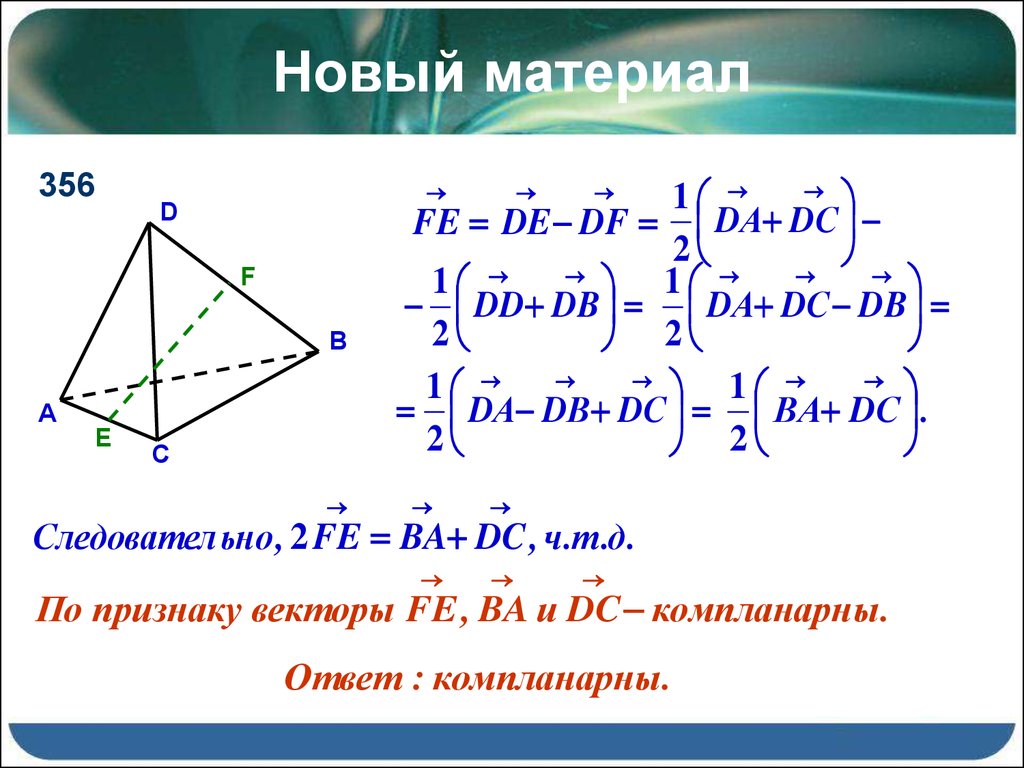
356
Дано : АВСD тетраэдр
D
Е середина АС ,
F
B
F середина BD .
Доказать : 2 FE ВА DC .
A
E
C
Компланарны ли векторы FE , BA и DC?

8. Новый материал

356
D
F
B
A
E
1
DА
DС
FE DE DF
2
1
1
DD DB DА DС DB
2
2
1
1
DА DВ DС ВА DС .
2
2
C
Следовател ьно , 2 FE BA DC , ч .т .д .
По признаку векторы FE , BA и DC компланарны .
Ответ : компланарны .

9. Новый материал

Определение.
Разложить вектор p по векторам a и b , это значит ,
представит ь его в виде р х а у b .
Утверждение, обратное признаку компланарности
векторов:
Если векторы р , а и b компланарны , то вектор р можно
представит ь в виде р х а у b , где х и у некоторые числа .
Докажем это.

10. Новый материал

Доказатель ство .
Пусть a и b неколлинеарны .
Отложим от некоторой точки пространст ва О
Р
В
p
b
Р1
Так как векторы компланарны,
то они лежат в одной плоскости.
векторы р , a и b .
Проведем через точку Р прямую , параллельн ую
О
А
а
ВО .
Тогда ОР ОР1 Р1 Р , но ОР1 х а , т .к . ОР1 || а , Р1 Р у b , т .к . Р1 P || b ,
следовател ьно , ОР х а у b ,
А если р || b , то р 0 а у b .
т .е , р х а у b , ч .т .д .

11. Новый материал

Мы умеем на плоскости складывать векторы по
правилу треугольника и параллелограмма. А если в
пространстве?
Для сложения трех некомпланарных векторов
пользуются правилом параллелепипеда. В чем оно
заключается?
B1
D
A1
С
c
b
О
В
Е
а
А
а b c OA OB OC OE OC OD

12. Решение упражнений

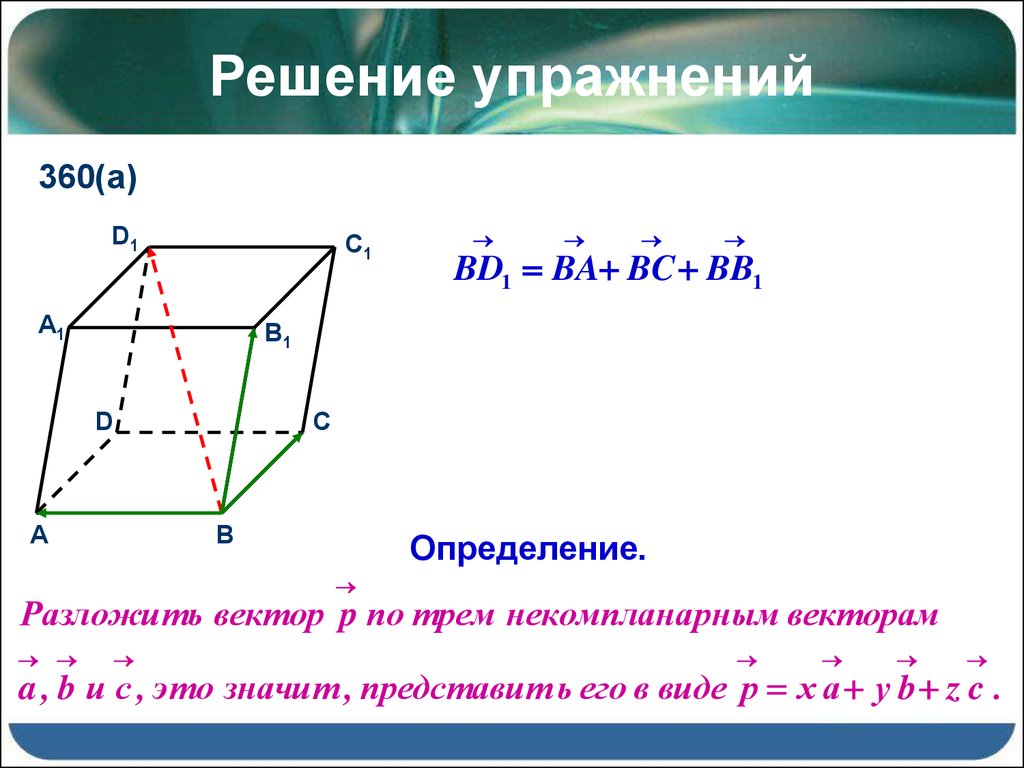
360(а)
D1
C1
A1
BD1 BA BC BB1
B1
D
A
C
B
Определение.
Разложить вектор p по трем некомпланарным векторам
a , b и с , это значит , представит ь его в виде р х а у b z c .

13. Домашнее задание

п. 39, 40
вопросы 13-15 стр. 97
358, 360(б), 368(а, б)