Similar presentations:
Планарные графы
1. Планарные графы
Лекция 62. Определение планарного графа
Граф,изображенный на
плоскости или на шаре,
называется плоским или
планарным графом, если его
ребра (дуги) не пересекаются
в точках, отличных от вершин
графа.
3. ПРИМЕРЫ
Планарный графНепланарный граф
1
2
1
2
5
3
5
3
4
4
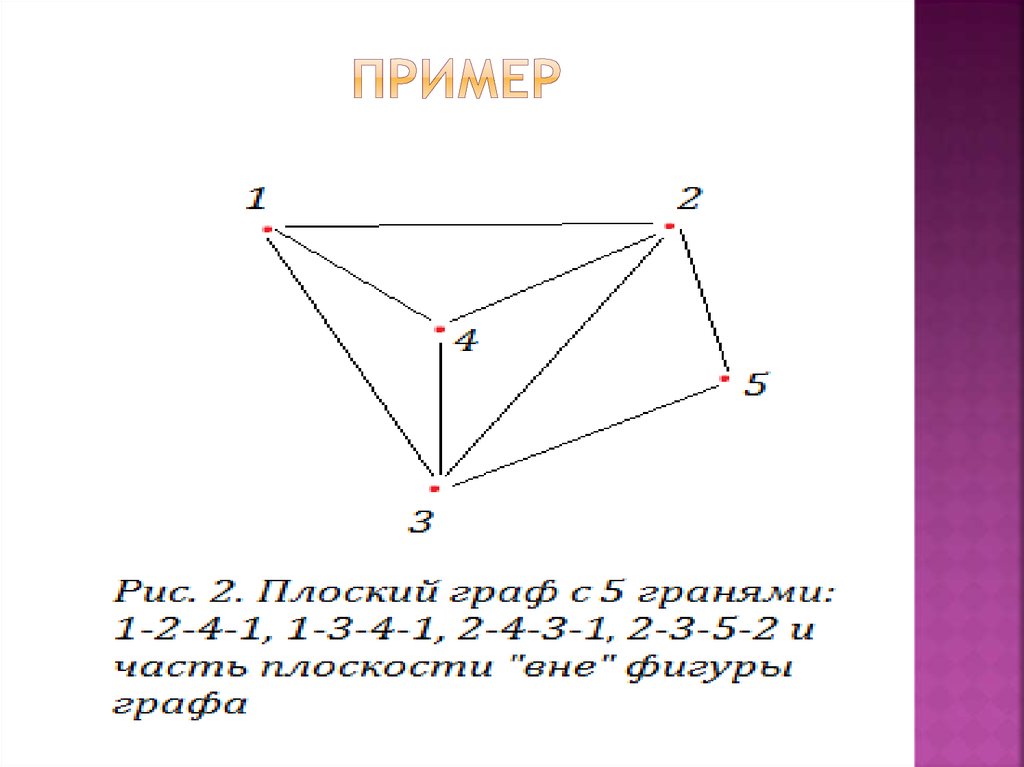
4. Что такое «грань»
Гранью (страной) вплоском представлении
графа называется часть
плоскости, ограниченная
простым циклом и не
содержащая внутри
других циклов.
5. пример
6. Экскурс в историю
Интереск планарным графам возник в
эпоху великих географических открытий:
высоко ценились точные и четкие карты,
но чем больше красок использовались на
карте, тем она дороже. Отсюда задача:
сколько красок нужно, чтобы все
страны на ней, имеющие общую
границу, были окрашены в разный
цвет, а число этих красок было
минимально?
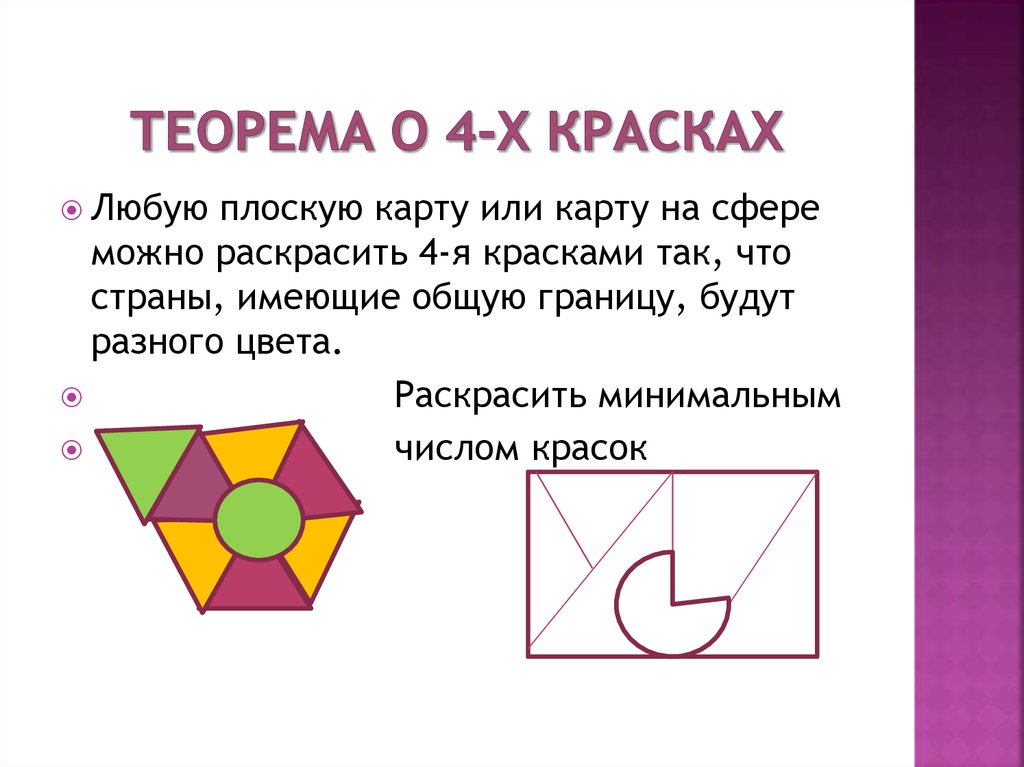
7. ТЕОРЕМА О 4-Х КРАСКАХ
Любуюплоскую карту или карту на сфере
можно раскрасить 4-я красками так, что
страны, имеющие общую границу, будут
разного цвета.
Раскрасить минимальным
числом красок
8. САМОСТОЯТЕЛЬНО РАСКРАСИТЬ МИНИМАЛЬНЫМ ЧИСЛОМ КРАСОК
9. САМОСТОЯТЕЛЬНО
Длякаких из этих тел справедлива
теорема о четырех красках?
10. Теорема эйлера
ПустьВ - количество вершин в
графе, Г - количество граней в
плоском представлении графа, Р количество рёбер в графе. Тогда
получаем формулу Эйлера для
связного планарного графа:
В+Г-Р=2
11. Примеры
G1(X,U)G2(X,U)
2
2
1
3
1
3
4
5
4
12. Формула эйлера для несвязного графа
Для несвязногопланарного графа с K
компонентами связности
формула Эйлера имеет
вид:
В + Г - Р = K + 1.
13. пример
Несвязный планарный граф с К = 3компонентами:
1
2
5
6
7
3
4
8
В+Г-Р=К+1
9
14. Теорема куратовского - понтрягина
Граф планарен тогда и только тогда, когдаон не содержит подграфов типов,
приведённых ниже:
15. Самостоятельно проверить планарность графа
32
4
7
1
5
6
16. САМОСТОЯТЕЛЬНО
Проверитьпланарность графов,
приведенных ниже в
персональных
заданиях.
17. Персональные задания 1- 6
01
1
1
1
0
1
1
1
0
0
1
0
1
1
1
0
1
0
0
1
0
1
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
0
0
0
1
0
1
0
1
0
1
0
0
1
0
0
0
1
1
0
1
0
1
1
0
1
0
0
0
1
0
1
0
1
0
0
1
0
№1
№2
№3
0
1
0
1
0
0
0
0
1
1
0
1
1
0
1
1
0
1
0
1
0
0
1
1
1
1
0
1
0
0
0
1
0
1
1
0
1
0
1
1
1
1
0
0
1
1
0
1
0
1
1
1
1
0
0
0
0
0
0
1
0
1
1
1
0
1
1
1
0
0
1
0
1
1
0
№4
№5
№6
26
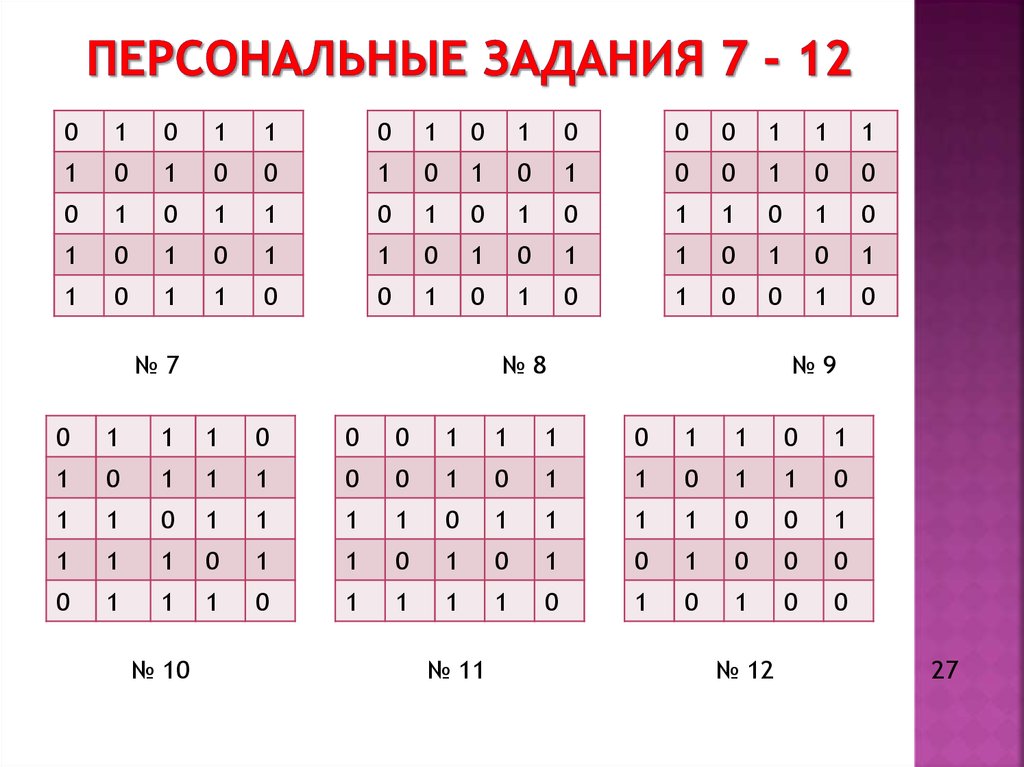
18. Персональные задания 7 - 12
01
0
1
1
0
1
0
1
0
0
0
1
1
1
1
0
1
0
0
1
0
1
0
1
0
0
1
0
0
0
1
0
1
1
0
1
0
1
0
1
1
0
1
0
1
0
1
0
1
1
0
1
0
1
1
0
1
0
1
1
0
1
1
0
0
1
0
1
0
1
0
0
1
0
№7
№8
№9
0
1
1
1
0
0
0
1
1
1
0
1
1
0
1
1
0
1
1
1
0
0
1
0
1
1
0
1
1
0
1
1
0
1
1
1
1
0
1
1
1
1
0
0
1
1
1
1
0
1
1
0
1
0
1
0
1
0
0
0
0
1
1
1
0
1
1
1
1
0
1
0
1
0
0
№ 10
№ 11
№ 12
27
19. Персональные задания 13 - 18
01
0
1
1
0
1
0
1
1
0
1
0
1
1
1
0
1
0
1
1
0
1
0
1
1
0
1
1
0
0
1
0
1
1
0
1
0
0
0
0
1
0
1
1
1
0
1
0
1
1
0
0
0
1
1
1
1
0
1
1
1
1
1
0
1
1
0
1
0
1
0
1
1
0
№ 13
№ 14
№ 15
0
1
0
1
0
0
0
1
1
0
0
1
0
0
1
1
0
1
1
1
0
0
1
0
1
1
0
1
1
0
0
1
0
1
1
1
1
0
1
1
0
1
0
1
1
1
1
1
0
1
1
0
1
0
1
0
1
1
0
1
0
1
1
1
0
0
1
1
1
0
1
0
1
1
0
№ 16
№ 17
№ 18
28
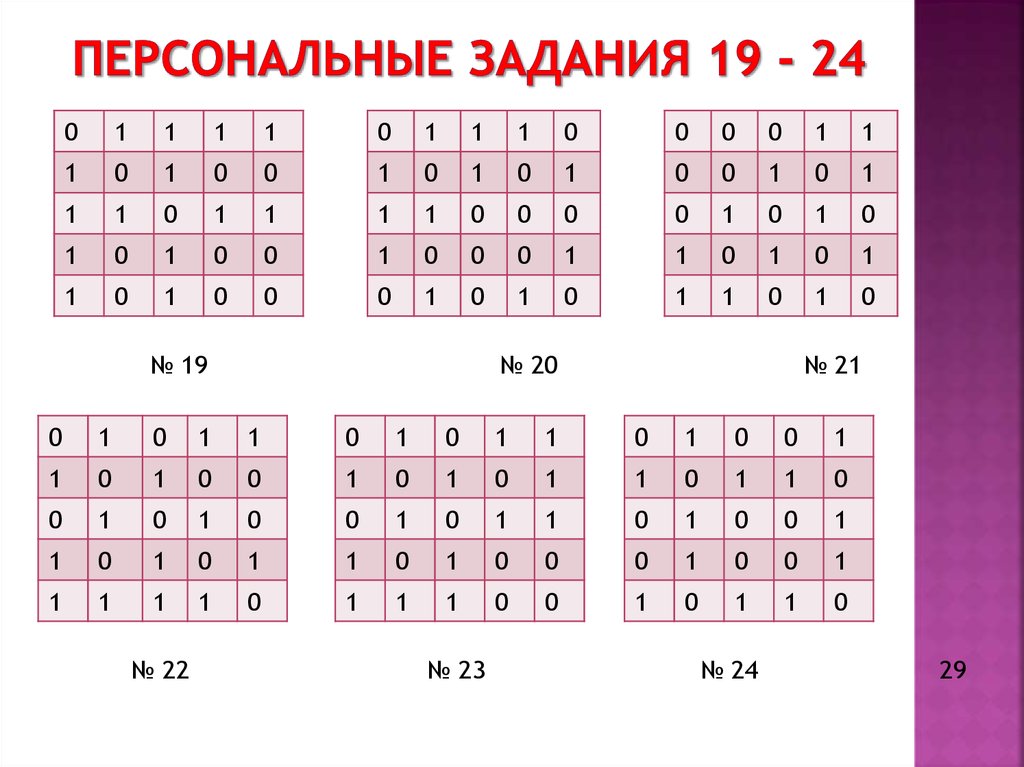
20. Персональные задания 19 - 24
01
1
1
1
0
1
1
1
0
0
0
0
1
1
1
0
1
0
0
1
0
1
0
1
0
0
1
0
1
1
1
0
1
1
1
1
0
0
0
0
1
0
1
0
1
0
1
0
0
1
0
0
0
1
1
0
1
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
1
0
№ 19
№ 20
№ 21
0
1
0
1
1
0
1
0
1
1
0
1
0
0
1
1
0
1
0
0
1
0
1
0
1
1
0
1
1
0
0
1
0
1
0
0
1
0
1
1
0
1
0
0
1
1
0
1
0
1
1
0
1
0
0
0
1
0
0
1
1
1
1
1
0
1
1
1
0
0
1
0
1
1
0
№ 22
№ 23
№ 24
29
















 mathematics
mathematics








