Similar presentations:
Теория графов. Планарные графы
1. Теория графов
Планарные графы2. ОПРЕДЕЛЕНИЕ
Планарным графом называется граф,который может быть изображен в
плоскости, так что его ребра не
пересекаются.
Граф, который не является планарным, называется непланарным.
2
3. Пример изображения графа как планарного
34. Пример изображения графа как планарного
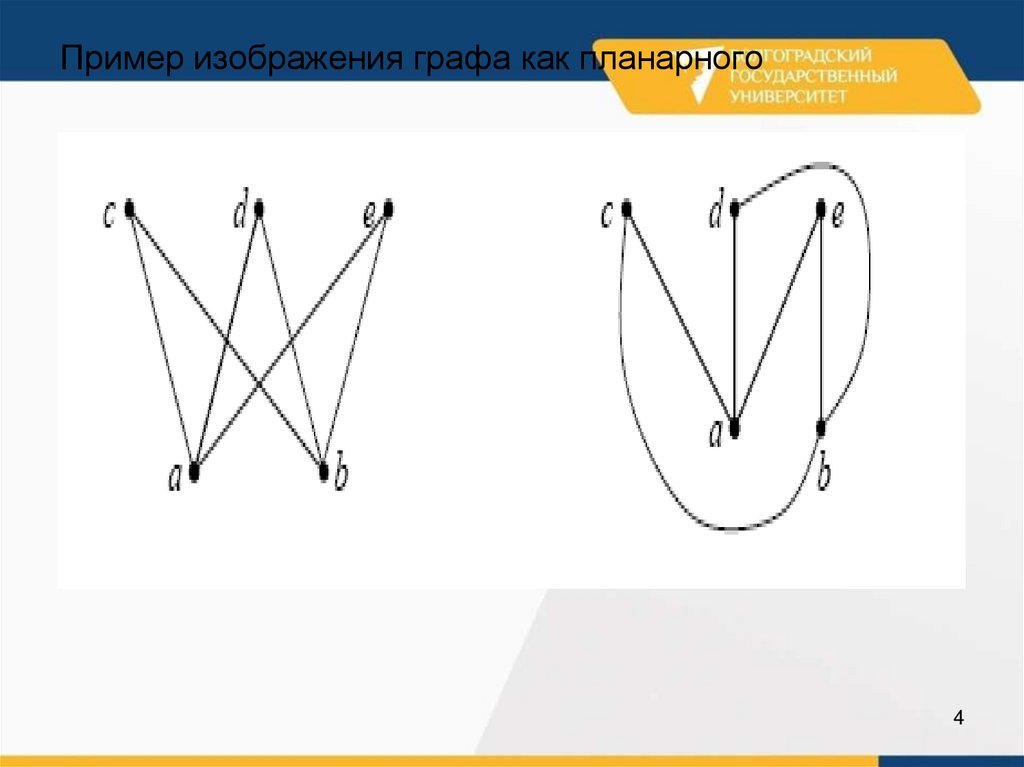
45. Пример изображения графа как планарного
56. Понятие плоского графа
• Плоским графом называется граф,вершины которого являются точками
плоскости,
а ребра – непрерывными плоскими
линиями без самопересечений, которые
соединяют соответствующие вершины
так, что никакие два ребра не имеют
общих точек, кроме инцидентной им
обоим вершиной.
6
7.
• Граф называется планарным, если онизоморфен некоторому плоскому
графу.
7
8.
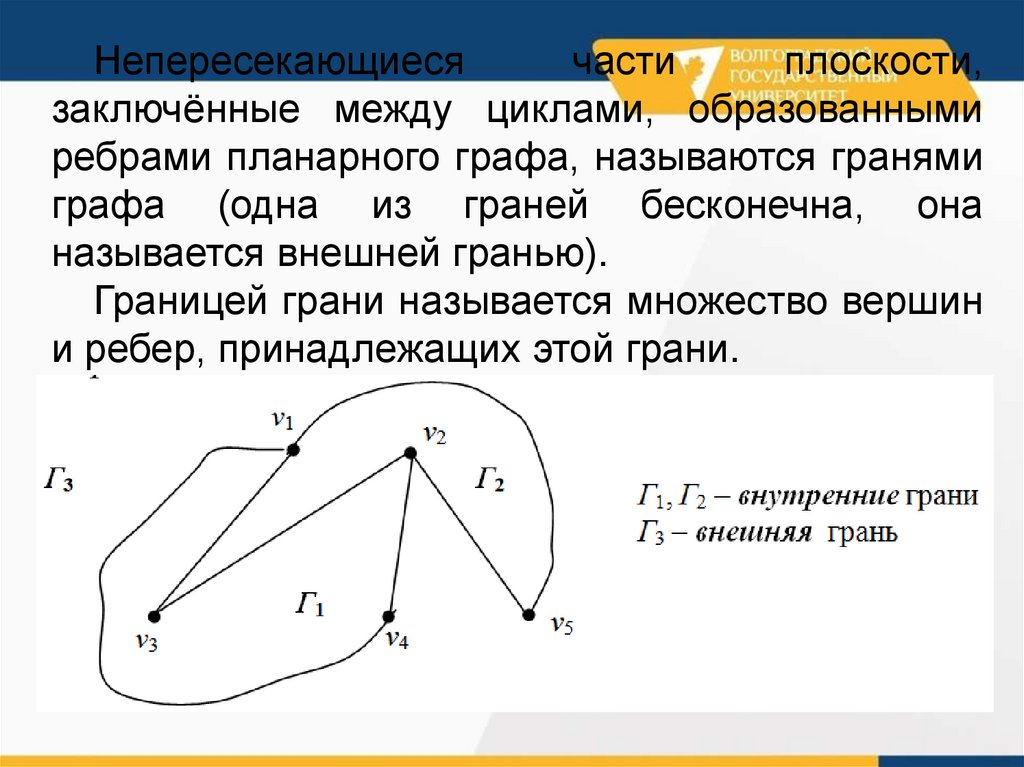
Непересекающиесячасти
плоскости,
заключённые между циклами, образованными
ребрами планарного графа, называются гранями
графа (одна из граней бесконечна, она
называется внешней гранью).
Границей грани называется множество вершин
и ребер, принадлежащих этой грани.
9.
• Всегда имеется одна неограниченнаявнешняя грань, все остальные грани
называются внутренними.
• Если в плоском графе нет циклов, то у
него имеется только одна грань.
9
10. Задача Эйлера
Задача. Три соседа имеют три общих колодца. Можно липровести непересекающиеся дорожки от каждого дома к
каждому колодцу?
То, что не получилось на рисунке, не является
доказательством невозможности соединения дорожками
домиков и колодцев. Для доказательства воспользуемся
следующей теоремой Эйлера.
11. Теорема Эйлера
ТЕОРЕМА.Если G – связный планарный граф,
содержащий υ вершин, e ребер и f
граней, то υ – e + f = 2.
11
12.
Доказательство.Пусть G – связный планарный граф, который имеет k
вершин. Рассмотрим некоторый остов этого графа. Остов
имеет всего одну внешнюю грань f=1, v=k вершин и e=k-1
ребер,
т.е.
v - e + f = k - (k - 1) + 1 = 2.
Будем поочередно добавлять к остову недостающие
ребра графа G. При каждом добавлении число вершин не
изменится, число ребер увеличивается на единицу, так же
как и число граней, поскольку при добавлении к остову
ребра,
связывающего
две
несмежные
вершины,
получается цикл, разделяющий текущую грань на две.
Таким образом, формула будет верна для всякого
графа, получающегося в результате таких операций, а
поскольку графом G заканчивается вся эта процедура, то
эта формула будет верна и для него.
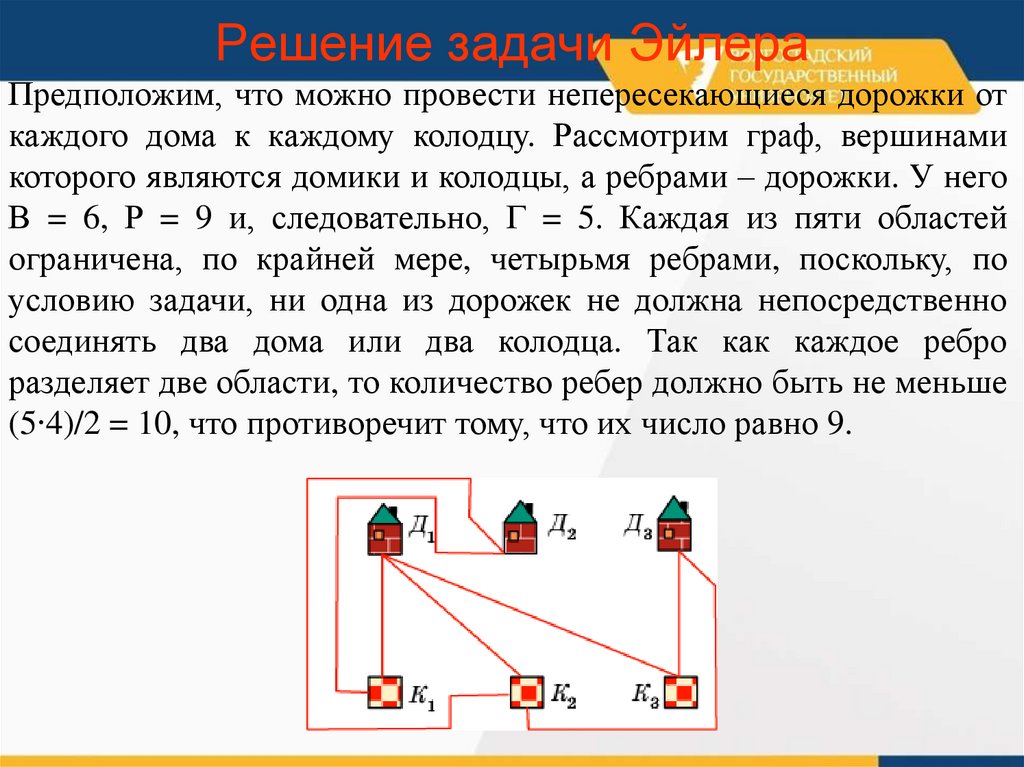
13. Решение задачи Эйлера
Предположим, что можно провести непересекающиеся дорожки откаждого дома к каждому колодцу. Рассмотрим граф, вершинами
которого являются домики и колодцы, а ребрами – дорожки. У него
В = 6, Р = 9 и, следовательно, Г = 5. Каждая из пяти областей
ограничена, по крайней мере, четырьмя ребрами, поскольку, по
условию задачи, ни одна из дорожек не должна непосредственно
соединять два дома или два колодца. Так как каждое ребро
разделяет две области, то количество ребер должно быть не меньше
(5∙4)/2 = 10, что противоречит тому, что их число равно 9.
14.
ТЕОРЕМА.Полный двудольный граф K3,3 не
является планарным.
14
15.
• Лемма.В произвольном связном планарном
графе G с количеством вершин не
менее трех имеет место неравенство
3υ – e ≥ 6.
15
16.
• ТЕОРЕМА.Полный граф K5 не является
планарным.
16
17. Доказательство:
• Граф К5 имеет пять вершин и десятьребер.
• 3υ – e = 3*5 – 10 = 5
• Согласно Лемме: в произвольном
связном планарном графе G с
количеством вершин не менее трех имеет
место неравенство 3υ – e ≥ 6.
Следовательно граф К5 непланарный.
17
18. Признак планарности/непланарности графов
19.
Графы Понтрягина - Куратовского, играют важнуюроль в теории планарности графов. Они не являются
планарными графами.
Граф K5 представляет собой полный граф наименьшего
порядка, который, не являясь планарным графом (полные
графы K2, K3, K4 - планарные), становится планарным
после удаления хотя бы одного его ребра.
Второй (двудольный граф K33) является моделью
известной задачи о трех домах и трех колодцах.
20. Теорема Понтрягина-Куратовского
Граф планарен тогда и только тогда,когда он не содержит подграфов,
гомеоморфных К5 или К3,3.
20
21. Понятие гомеоморфности графов
• Два графа называются гомеоморфнымиили тождественными с точность до
вершины степени 2, если они могут быть
получены с одного и того же графа с
помощью операции введения вершины в
ребро степени 2.
21
22. Операция введения вершины в ребро
• Добавлением вершины w в ребро (u,v)называется операция, в результате
которой получаем два ребра (u,w) и (w,v),
а ребро (u,v) удаляется из графа G.
22
23. Примеры
2324. Примеры
2425. Эквивалентная форма критерия планарности
• Теорема.Граф планарен тогда и только тогда,
когда в нем нет подграфов,
стягиваемых к графам К5 или К3,3.
25
26. Примеры
2627.
• Теорема.Если два связных графа гомеоморфны,
то они либо оба планарны, либо оба
непланарны.
• Теорема.
Произвольный граф, гомеоморфный
графу К3,3 или К5,не является
планарным.
27
28.
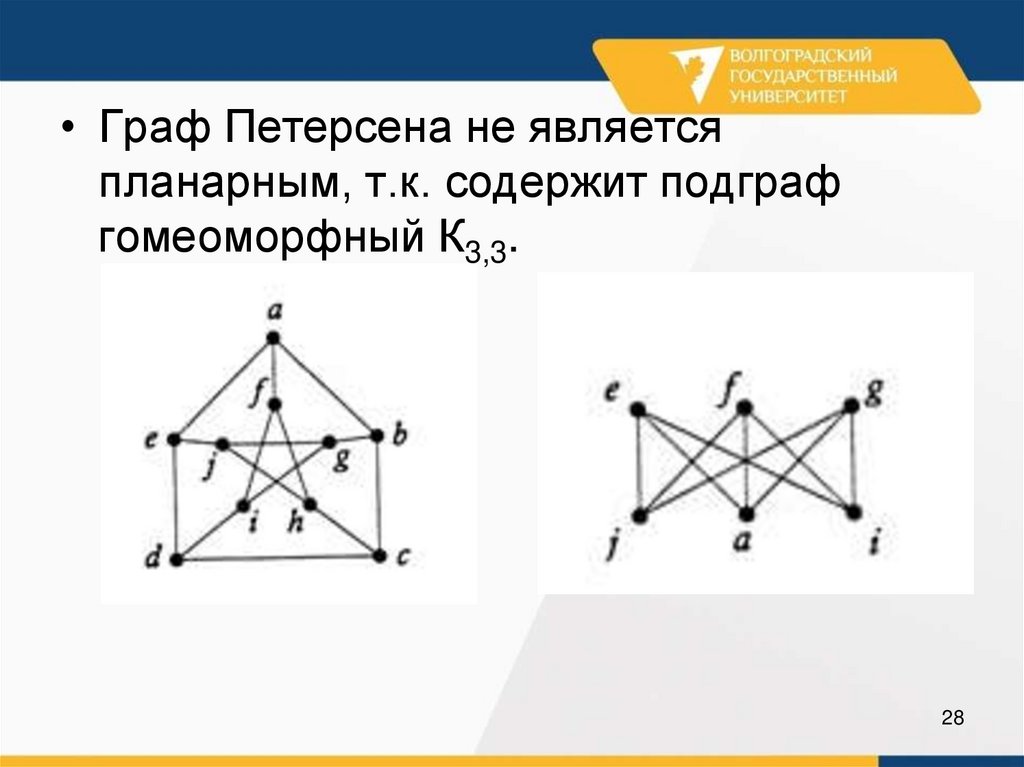
• Граф Петерсена не являетсяпланарным, т.к. содержит подграф
гомеоморфный К3,3.
28
29. Гамма-алгоритм
На вход подаются графы, обладающие следующимисвойствами:
• граф связный;
• граф имеет хотя бы один цикл;
• граф не имеет мостиков, т. е. ребер, после удаления
которых граф распадается на две компонеты
связности.
Если нарушено свойство (1), то граф нужно укладывать
отдельно по компонентам связности.
Если нарушено свойство (2), то граф — дерево и
нарисовать его плоскую укладку тривиально.
29
30.
Случай нарушения свойства (3) рассмотримболее подробно. Если в графе есть мостики, то их
нужно разрезать, провести отдельно плоскую
укладку каждой компоненты связности, а затем
соединить их мостиками.
Здесь может возникнуть трудность: в процессе
укладки концевые вершины мостика могут
спрятаться внутри плоского графа. Нарисуем
одну компоненту связности и будем присоединять
к ней другие последовательно. Каждую новую
компоненту связности будем рисовать в той
грани, в которой лежит концевая вершина
соответствующего мостика. Так как граф
связности мостиками компонент связности
является деревом, мы сумеем получить плоскую
укладку.
30
31.
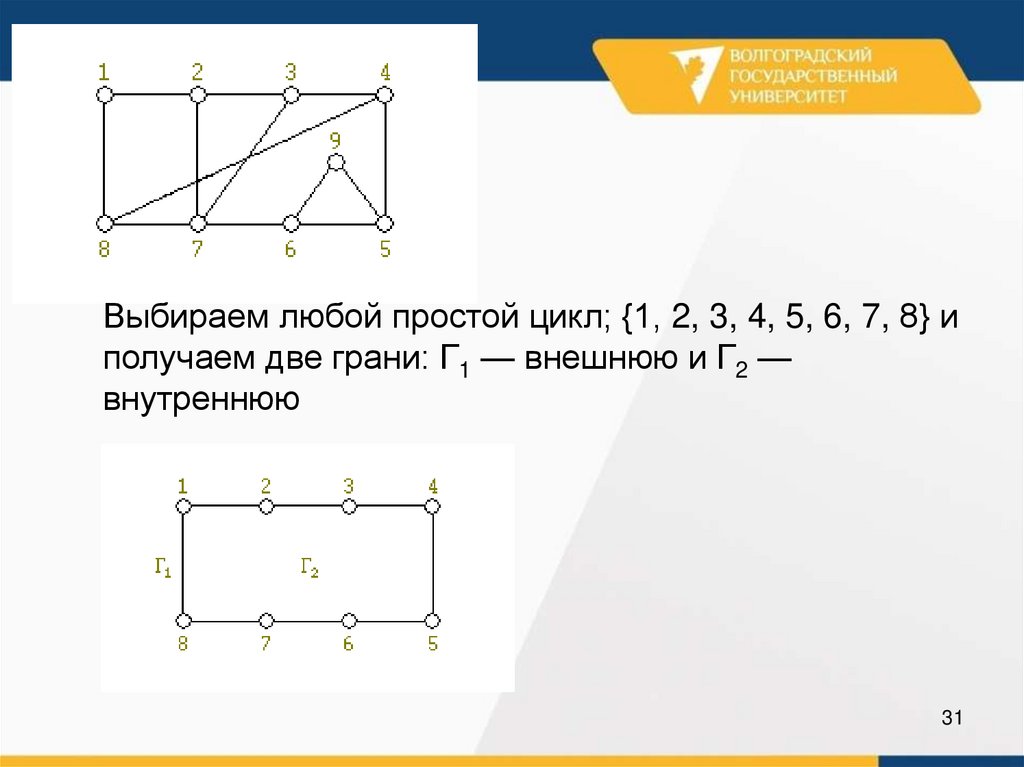
Выбираем любой простой цикл; {1, 2, 3, 4, 5, 6, 7, 8} иполучаем две грани: Γ1 — внешнюю и Γ2 —
внутреннюю
31
32.
Обозначим выбранный цикл как G′. На каждом шаге будем строитьмножество сегментов. Каждый сегмент S относительно уже
построенного графа G′ представляет собой одно из двух:
ребро, оба конца которого принадлежат G′, но само оно не
принадлежит G′;
связную компоненту графа G – G′, дополненную всеми ребрами
графа G, один из концов которых принадлежит связной компоненте, а
второй из графа G′.
Те вершины, которые одновременно принадлежат G′ и какому-то
сегменту, назовем контактными.
Контактные вершины обведены в квадрат.
32
33.
1. Выберем любой простой цикл C исходного графа G; изобразим егона плоскости в виде грани, которую примем за уже уложенную
часть G′; сформируем сегменты Si; если множество сегментов
пусто, то перейти к п. 3.
2. (Общий шаг). Пока множество сегментов непусто:
a) Для каждого сегмента S найти множество Γ(S). Если
существует сегмент S, для которого |Γ(S)| = 0, то граф не
планарный, конец.
b) Выбираем один из сегментов с минимальным числом,
вмещающих его граней.
c) Выбираем одну из подходящих граней для выбранного
сегмента.
d) В данном сегменте выбираем цепь между двумя контактными
вершинами и укладываем ее в выбранной грани. Учтем
изменения в структуре сегментов и перейдем к п. a).
3. (Завершение). Построена плоская укладка G′ исходного графа G,
конец.
33





























 mathematics
mathematics








