Планарные графы

1.

Планарные графы
Лектор: Завьялов Олег Геннадьевич
кандидат физико-математических наук, доцент
1

2.

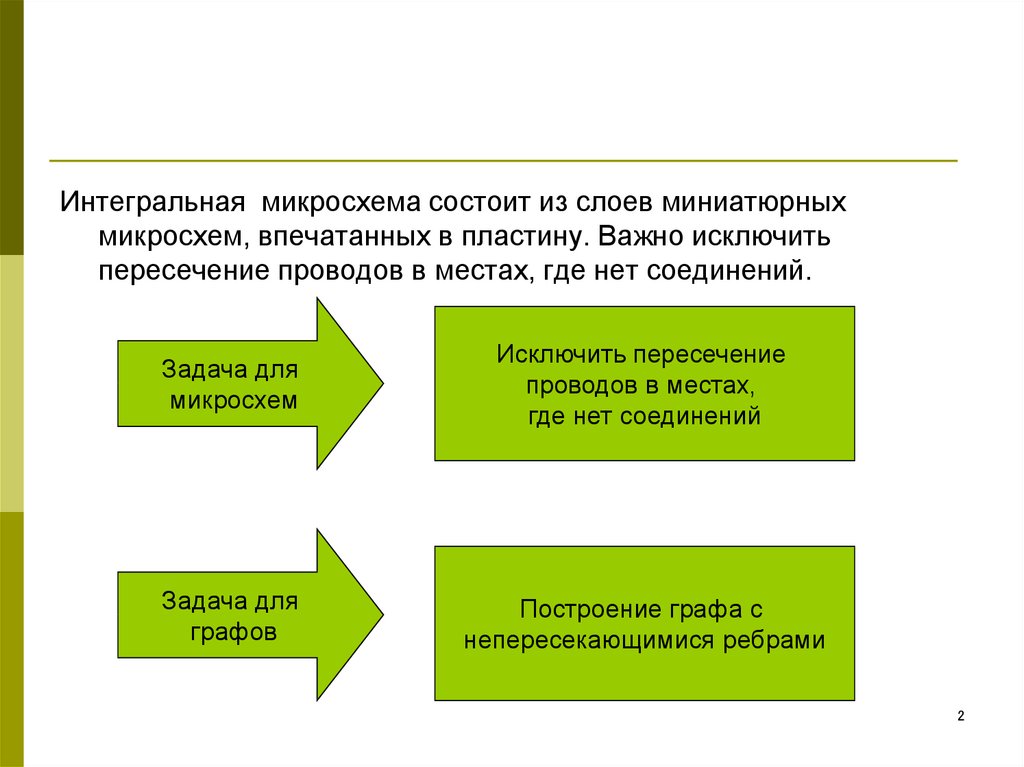
Интегральная микросхема состоит из слоев миниатюрных
микросхем, впечатанных в пластину. Важно исключить
пересечение проводов в местах, где нет соединений.
Задача для
микросхем
Исключить пересечение
проводов в местах,
где нет соединений
Задача для
графов
Построение графа с
непересекающимися ребрами
2

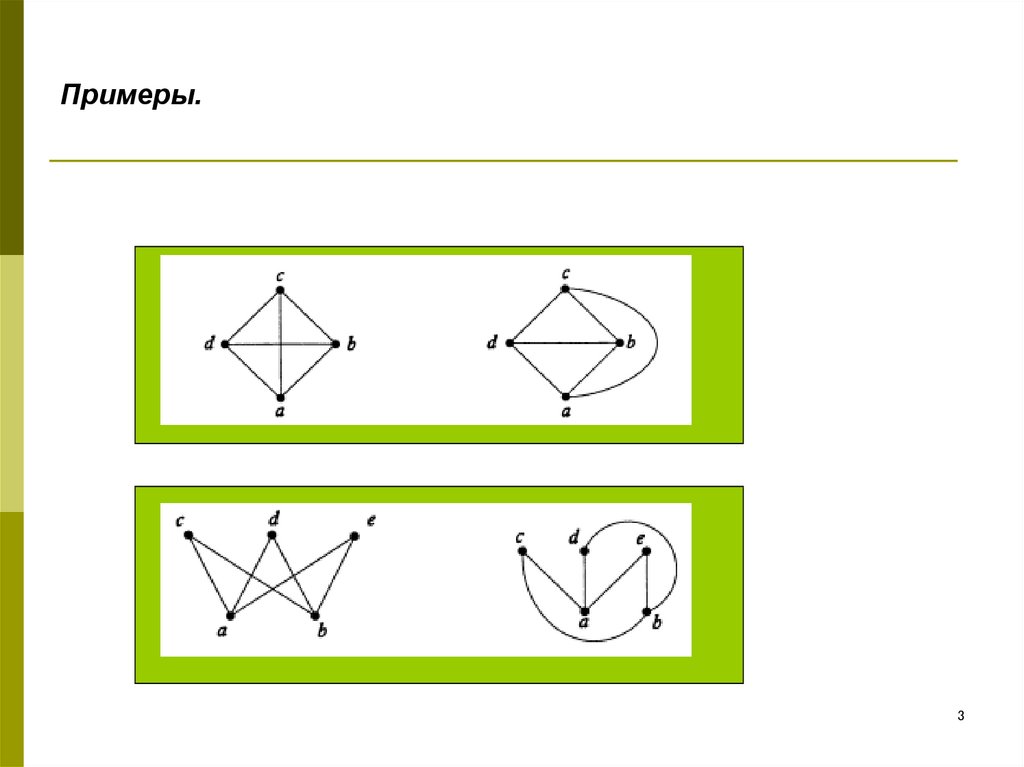
3. Примеры.

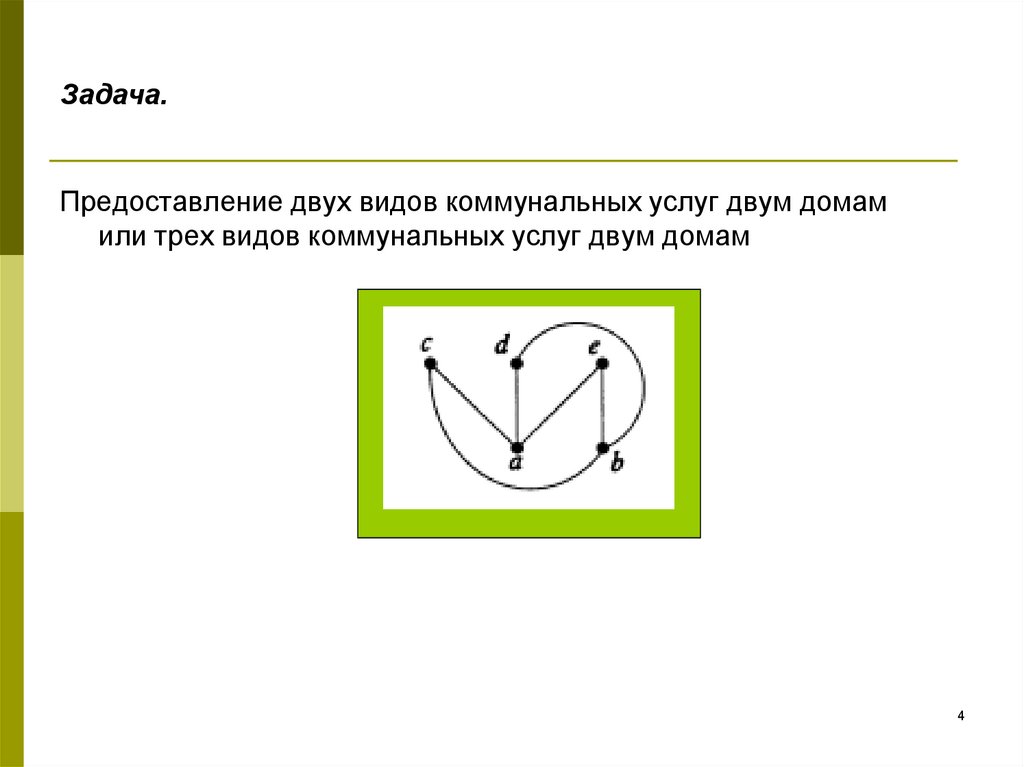
3

4. Задача.

Предоставление двух видов коммунальных услуг двум домам
или трех видов коммунальных услуг двум домам
4

5. Определения.

Планарным графом называется граф, который может быть
изображен в плоскости так, что его ребра не пересекаются.
Граф, который не является планарным, называется
непланарным.
Если граф планарен и нарисован так, что никакие линии не
пересекаются, и его необходимо разрезать вдоль ребер, то
граф окажется разделенным на части, включая внешнюю
часть. Такие части называются гранями. Граница каждой
грани является циклом.
Грань планарного графа – максимальный участок плоскости
такой, что любые две точки этого участка могут быть
соединены кривой, не пересекающей ребро графа.
5

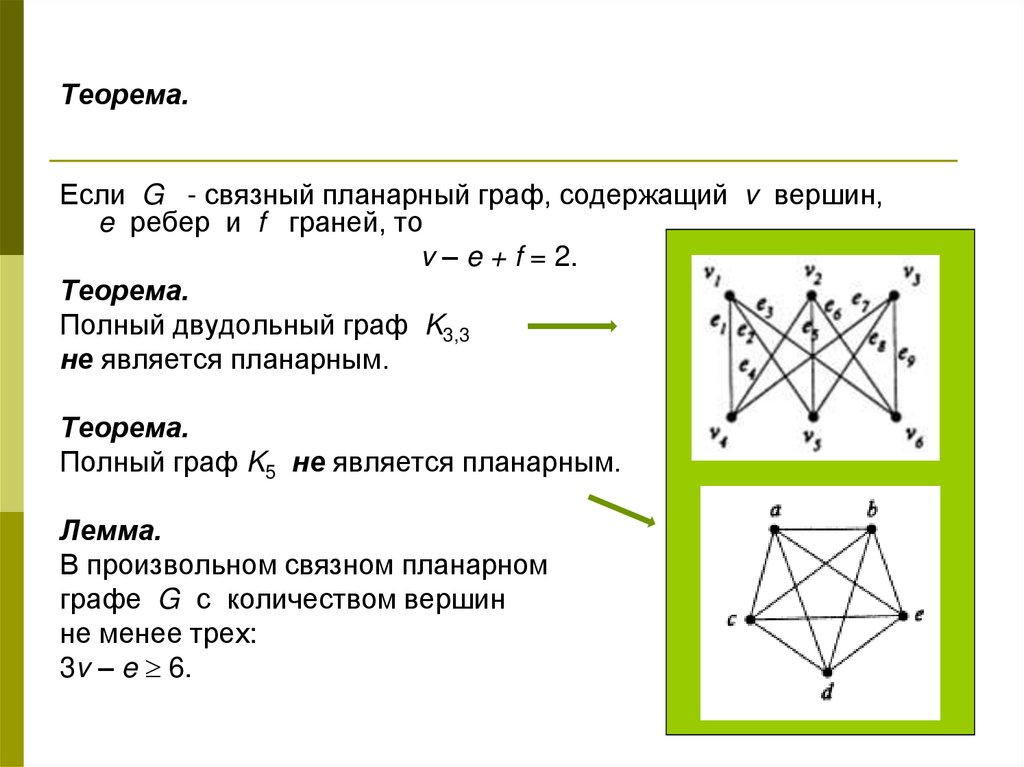
6. Теорема.

Если G - связный планарный граф, содержащий v вершин,
e ребер и f граней, то
v – e + f = 2.
Теорема.
Полный двудольный граф K3,3
не является планарным.
Теорема.
Полный граф K5 не является планарным.
Лемма.
В произвольном связном планарном
графе G с количеством вершин
не менее трех:
3v – e 6.
6

7. Теорема.

Каждый планарный граф G содержит вершину степени 5 или менее.
Теорема.
Если два связных графа гомеоморфны, то они либо оба планарны,
они либо оба непланарны.
Теорема.
Произвольный граф, гомеоморфный графу K3,3 или K5 , не является
планарным.
Теорема. (Куратовский)
Граф является планарным тогда и только тогда, когда он не содержит
подграф, гомеоморфный
K3,3 или K5 .
7

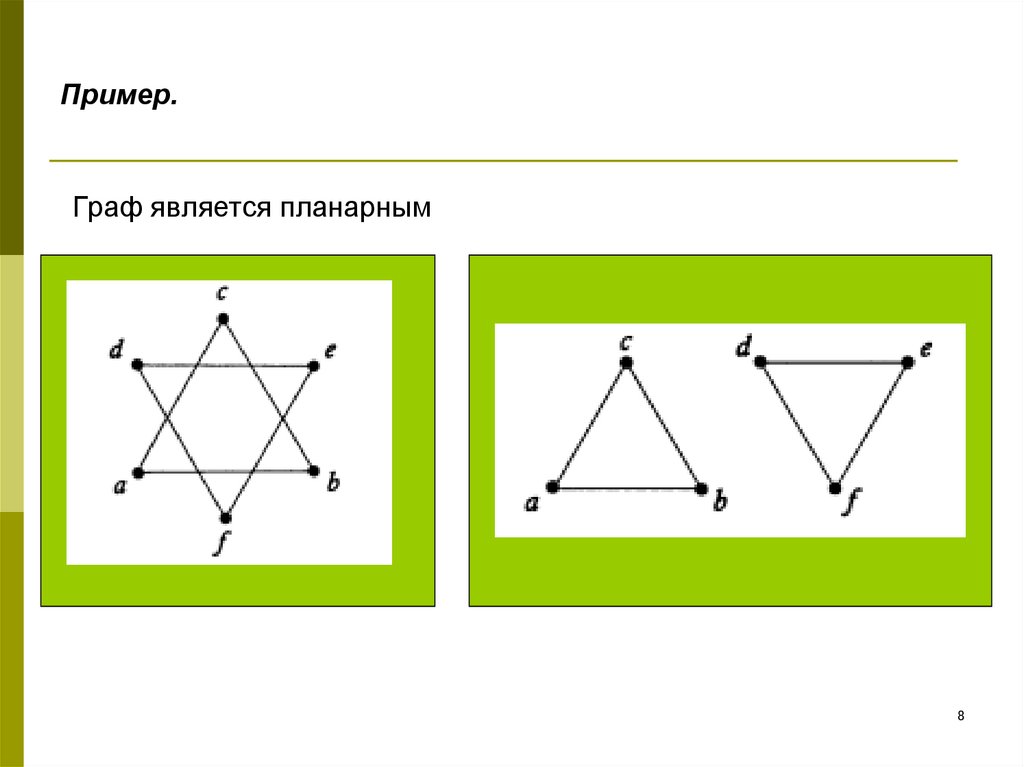
8. Пример.

Граф является планарным
8

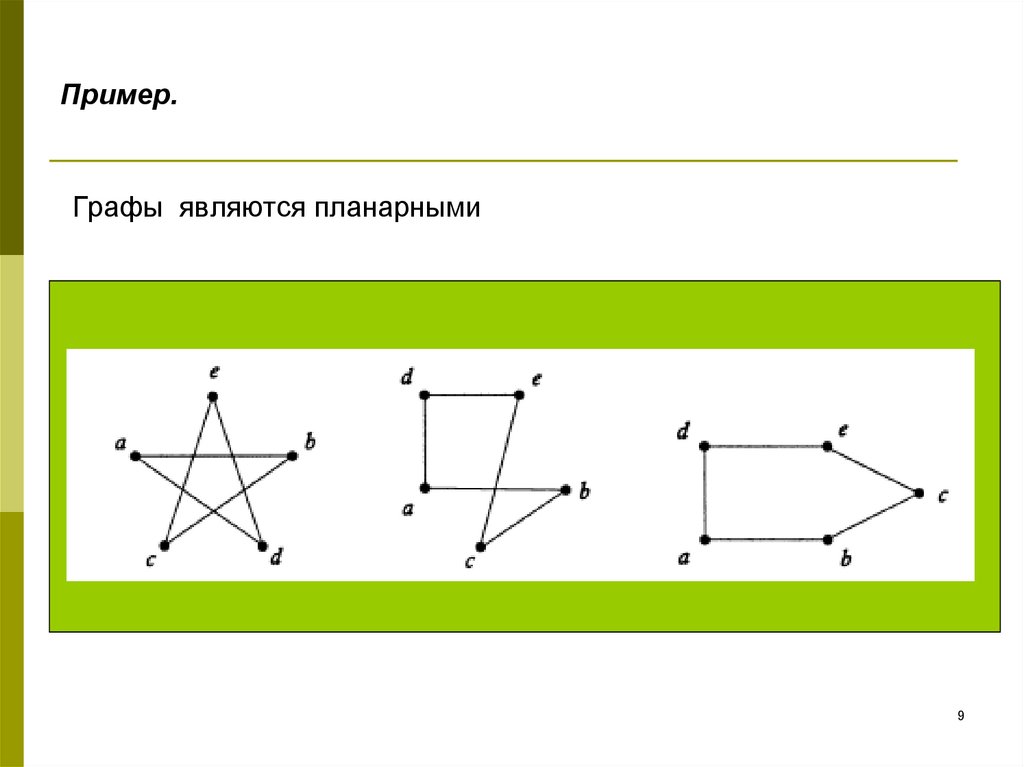
9. Пример.

Графы являются планарными
9

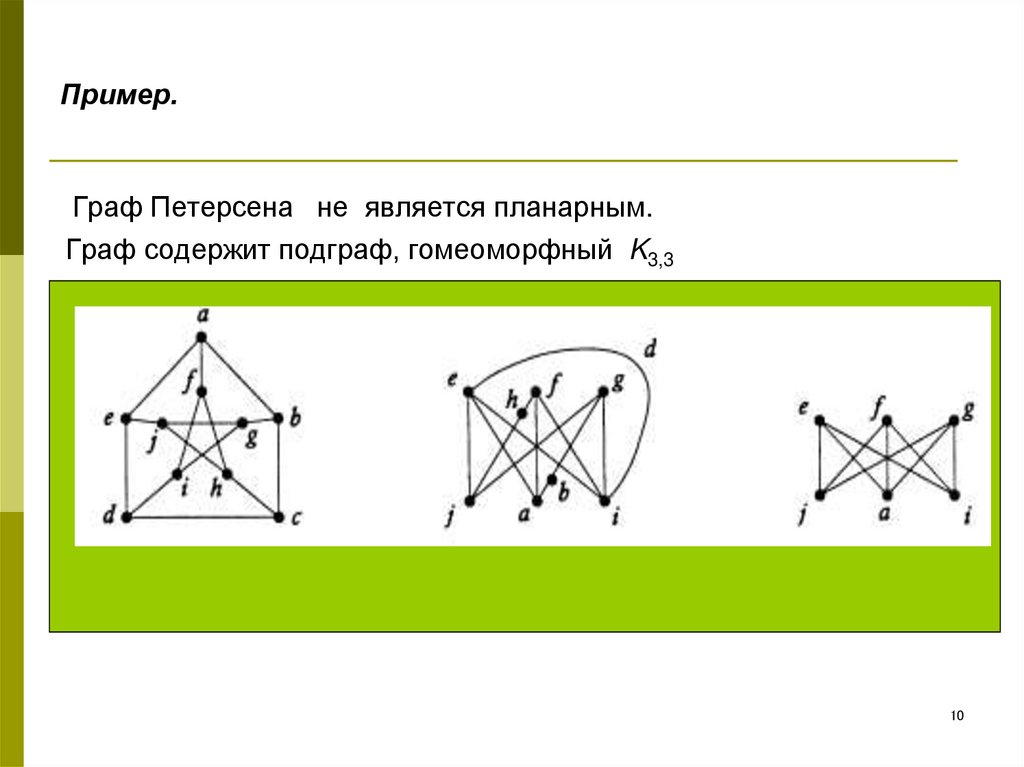
10. Пример.

Граф Петерсена не является планарным.
Граф содержит подграф, гомеоморфный K3,3
10

11.

Раскраска графов
11

12. Проблема 4-х красок.

Карту необходимо раскрасить, используя только 4 цвета так, чтобы
любые две граничащие страны были раскрашены разными цветами.
Известно, что:
Для раскрашивания карты 5 красок достаточно, а 3 – нет.
Задача решена численными расчетами перебором огромного числа
случаев.
12

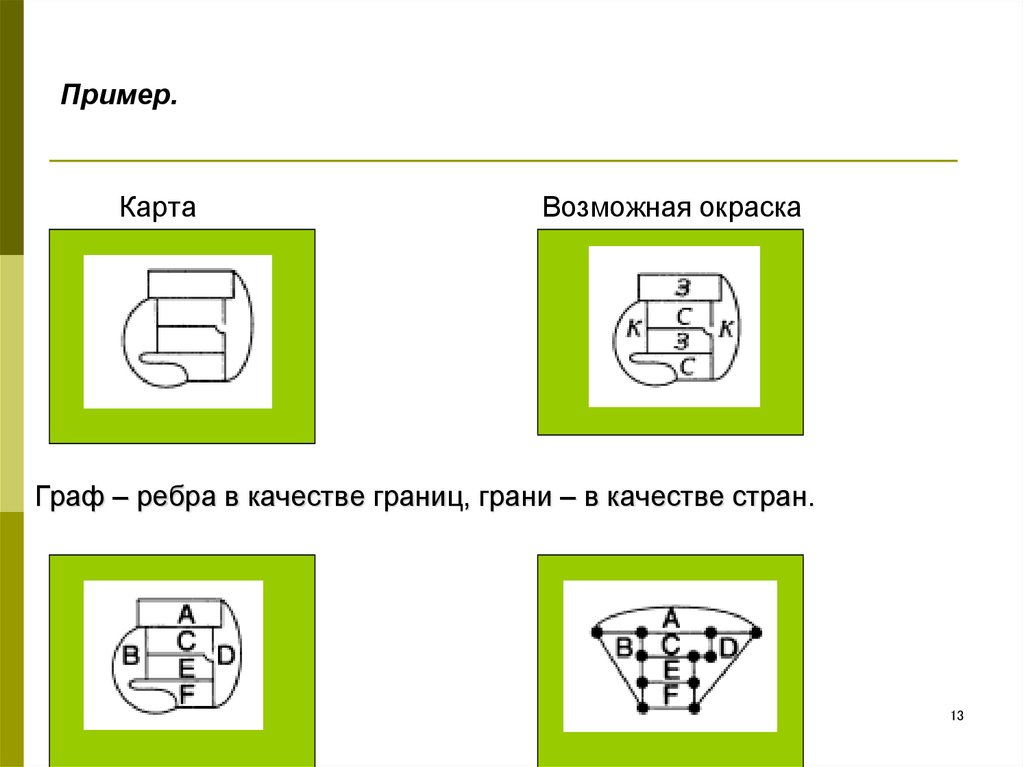
13. Пример.

Карта
Возможная окраска
Граф – ребра в качестве границ, грани – в качестве стран.
13

14. Пример.

Двойственный граф G' формируется путем замены граней (стран)
вершинами и соединения их ребрами, если грани в исходном графе
смежные.
В двойственном графе G' вершины являются смежными тогда и
только тогда, когда соответствующие грани являются смежными в
исходном графе G.
Двойственный граф G'
14

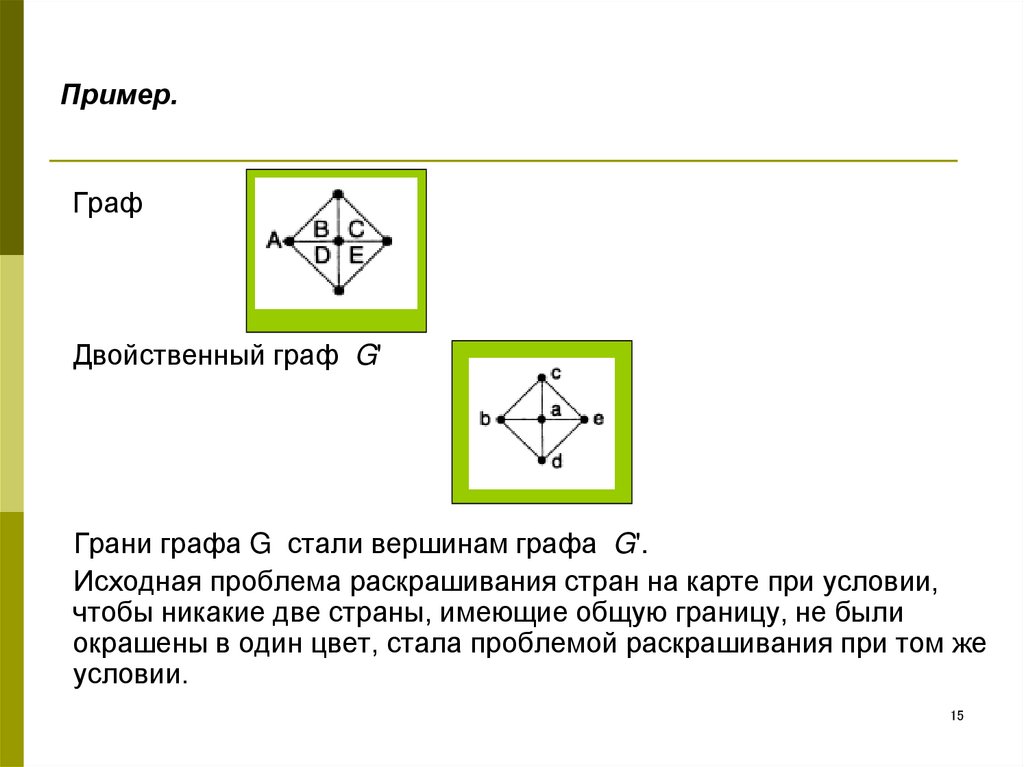
15. Пример.

Граф
Двойственный граф G'
Грани графа G стали вершинам графа G'.
Исходная проблема раскрашивания стран на карте при условии,
чтобы никакие две страны, имеющие общую границу, не были
окрашены в один цвет, стала проблемой раскрашивания при том же
15
условии.

16. Задача (Г.Д. Бирхгоф)(G.D. Birkhoff).

Зафиксируем для графа количество цветов.
Сколько существует способов раскрашивания вершин при условии,
что никакие две смежные не будут одного цвета?
Имеется 5 цветов и необходимо раскрасить граф.
5 цветов для раскрашивания 1-ой вершины,
4-ре цвета – для второй.
5 4 = 20 способов раскрашивания.
16

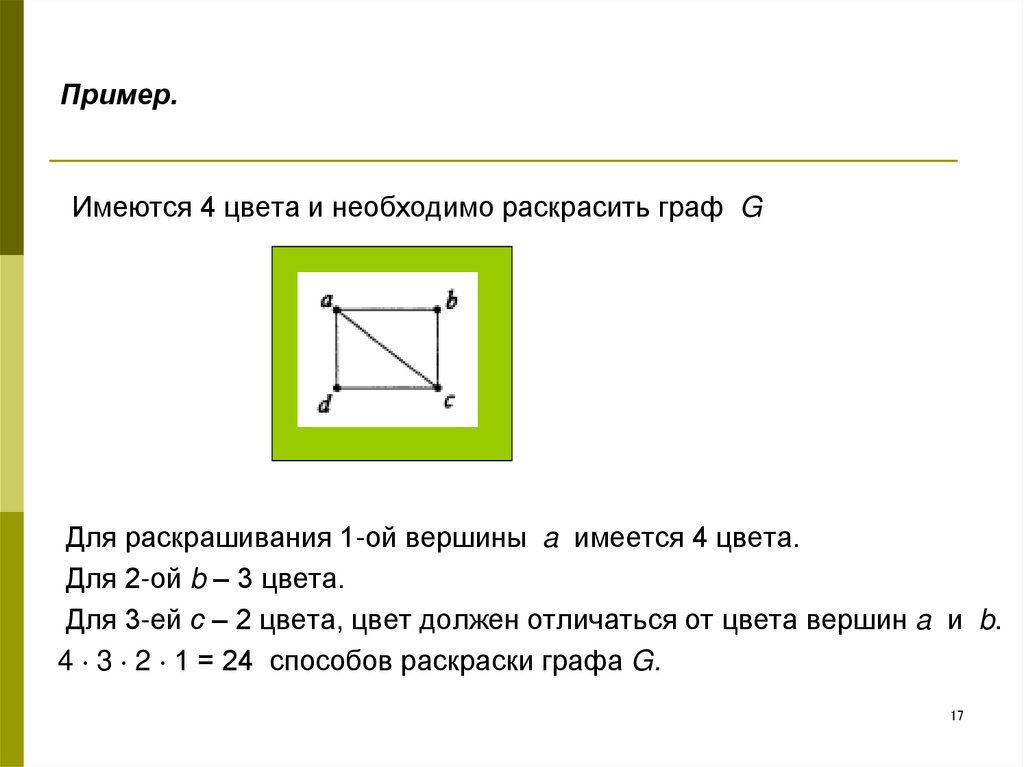
17. Пример.

Имеются 4 цвета и необходимо раскрасить граф G.
Для раскрашивания 1-ой вершины a имеется 4 цвета.
Для 2-ой b – 3 цвета.
Для 3-ей с – 2 цвета, цвет должен отличаться от цвета вершин a и b.
4 3 2 1 = 24 способов раскраски графа G.
17

18. Пример (предыдущий).

Имеется цветов для раскрашивания графа G.
Имеется цветов для раскрашивания вершины a,
-1 цветов для раскрашивания вершины b,
-2 цветов для раскрашивания вершины c,
-2 цветов для раскрашивания вершины d.
( - 1) ( - 2) ( - 3) = СG( ) способов раскраски графа G с
использованием цветов.
CG(0) = CG(1) = CG(2) = 0.
18

19. Определение.

Пусть G – граф. Раскраской графа G называется окрашивание
вершин графа G такое, что никакие две смежные вершины не имеют
один цвет.
Пусть СG( ) обозначает количество способов раскраски графа G с
использованием цветов, так что никакие две смежные вершины
не имеют один цвет, то есть СG( ) - количество способов раскраски
графа G.
Для фиксированного графа G функция СG( ) является
полиномиальной функцией от , называемой хроматическим
многочленом графа G.
Хроматическое число графа – это наименьшее число цветов,
которое используется для раскраски графа. Это наименьшее
положительное число n, что СG(n) = 0.
19

20. Пример.

Пусть граф G состоит из пяти изолированных вершин, так что в нем
нет ребер, нет смежных вершин.
Если раскрашивать граф цветами, то будем иметь вариантов
для каждой вершины, будет существовать
= 5
способов раскраски графа и СG( ) = 5 .
Если граф состоит из k изолированных вершин, СG( ) = k ,
хроматическое число = 1.
20

21. Пример.

Пусть G - граф K5 . Каждая из пяти вершин является смежной с
остальными 4-мя вершинами.
Граф раскрашиваем цветами,
для 1-ой вершины имеется вариантов цвета.
2-ая вершина смежная с 1-ой, имеется - 1 вариантов цвета.
3-я вершина смежная с 1-ой и со 2-ой, имеется - 2 вариантов
цвета.
4-ая вершина смежная с каждой из первых трех раскрашенных,
имеется - 3 вариантов цвета.
5-ая вершина смежная с каждой из первых 4-х, имеется - 4
вариантов цвета.
СG( ) = ( - 1) ( - 2) ( - 3) ( - 4) способов.
Граф G не может быть раскрашен 4-мя цветами, СG( ) = 0.
Граф G не является планарным не противоречит утверждению, что
планарный граф может быть окрашен 5-ю цветами.
21

22. Пример.

Пусть G - граф Kn .
СG( ) = ( - 1) ( - 2) ( - 3) … ( - (n - 1)) способов.
Хроматическое число графа G равно n.
22

23. Теорема.

Если G = G1 G2 G3 … Gn ,
где G1 , G2 , G3 , … , Gn - компоненты графа G,
то СG( ) = СG1( ) СG2( ) СG3( ) … СGn( ).
Следствие. СG( ) = 0 тогда и только тогда, когда СGn( ) = 0 для
некоторого 1 i n.
Следствие. Если для раскраски графа G требуется k цветов, то и для
одной из его компонент требуется для раскраски k цветов.
23

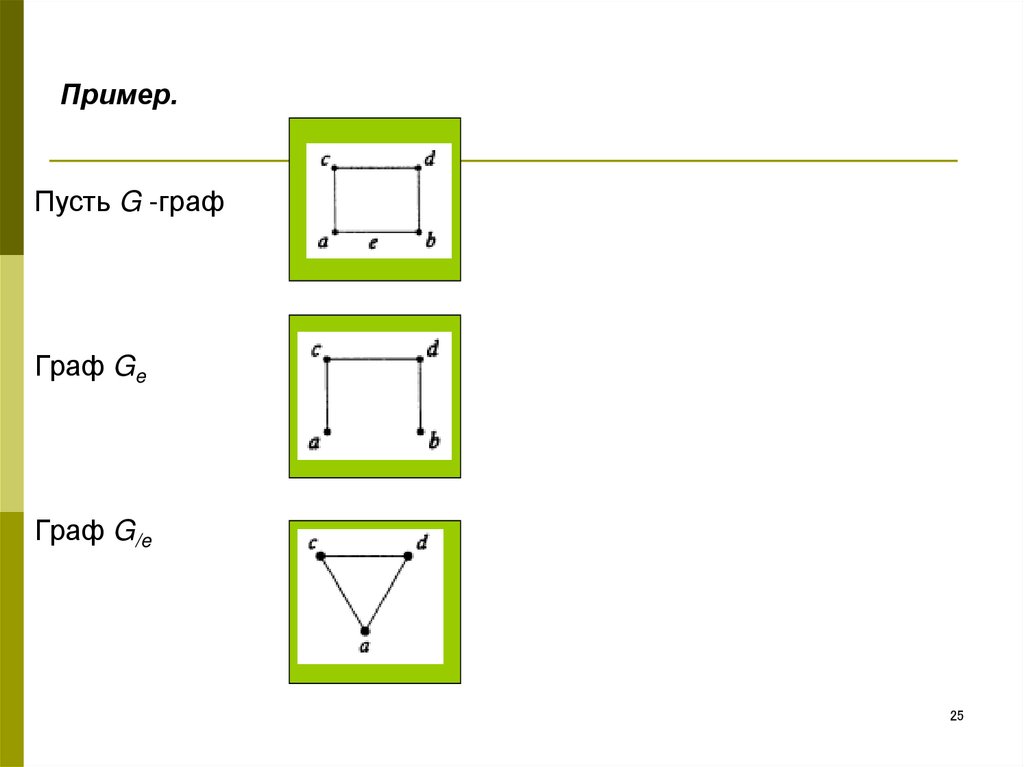
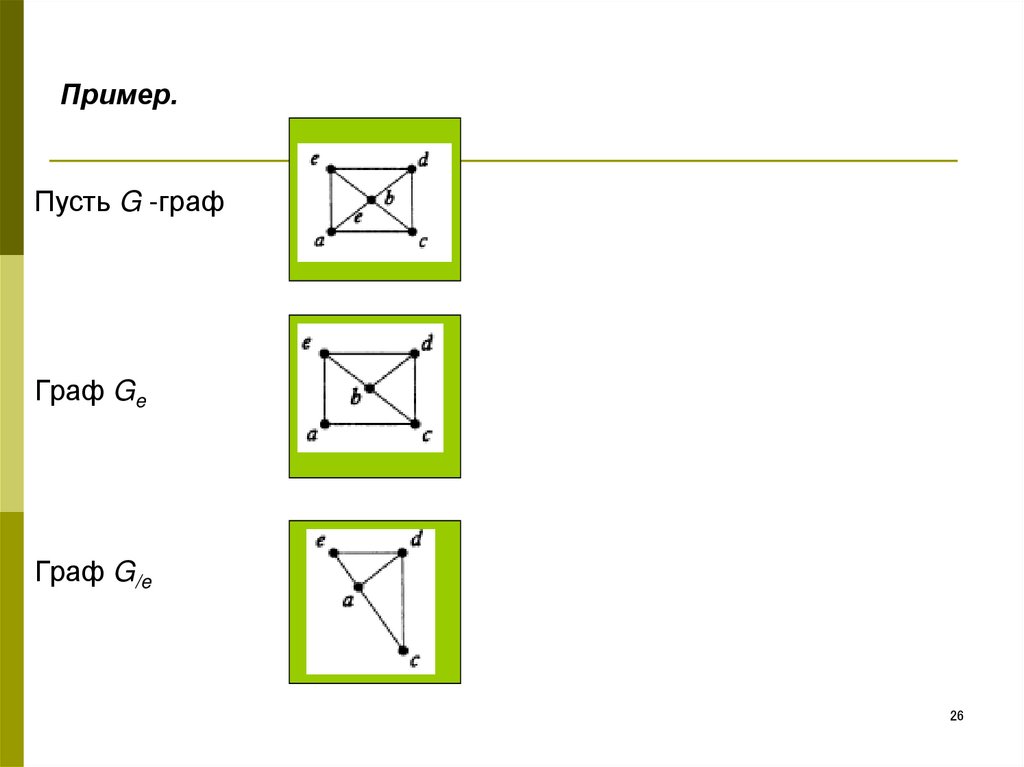
24.

Раскрашивание только связных графов.
Граф G( V, E). e = {a, b} - ребро.
Граф Ge - граф G, в котором удалено ребро e, но сохранены вершины
a и b.
Граф G/e - граф Gi с отождествленными (склеенными)
вершинами a и b.
Граф G/e - гомоморфным образом графа Gi ,
где гомоморфизм f : Ge G/e определен на всех вершинах графа Gi
f(a) = f(b) и f(v) = v для всех v из V – {a, b}.
Для ребер
f({u, v}) = {f (u), f(v)}.
f=f f
Функция с такими свойствами называется стягивающим
отображением.
24

25. Пример.

Пусть G -граф
Граф Ge
Граф G/e
25

26. Пример.

Пусть G -граф
Граф Ge
Граф G/e
26

27. Теорема.

Для произвольного планарного графа G с ребром e имеет место
равенство
CGe ( ) = CG ( ) + CG/e ( )
27

28. Теорема.

Для произвольного планарного графа G с n вершинами функция
СG ( ) представляет собой многочлен n –ой степени.
28

29. Теорема.

Для произвольного непустого связного графа G постоянный член в
СG ( ) равен 0. Если граф G имеет две или более вершин, то
сумма коэффициентов многочлена СG ( ) равна 0.
29

30. Теорема.

Произвольный планарный граф G можно раскрасить, используя
только пять цветов.
30

31.

Последний слайд лекции
!!