Similar presentations:
Эпюр №1. Точка, прямая, плоскость
1.
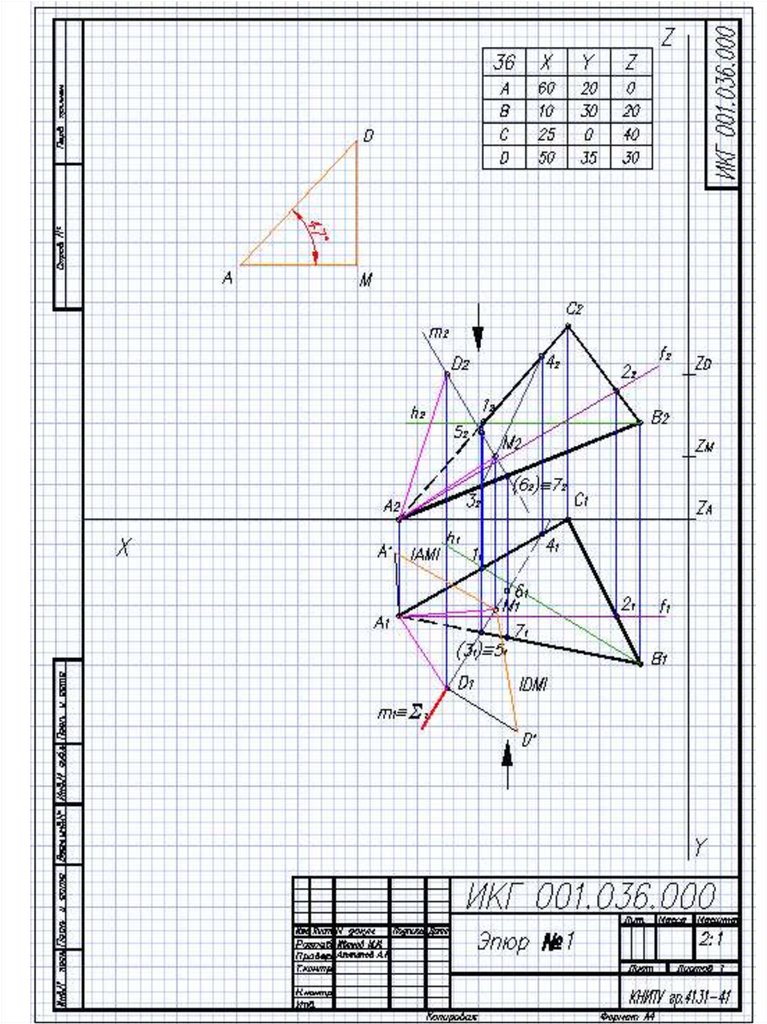
ЭПЮР №1ТОЧКА, ПРЯМАЯ, ПЛОСКОСТЬ
Определить натуральную величину
угла между прямой AD и
плоскостью треугольника ABC.
Выполнить графическое решение
задачи на формате А3 в масштабе 2:1
2.
913
17
21
25
29
20
0
60
5
10
55
25
55
0
50
20
55
40
70
0
65
60
0
45
15
5
0
40
60
20
5
50
55
0
25
45
50
2
6
10
14
18
22
26
30
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
0
50
20
50
65
20
10
20
20
0
45
0
10
45
25
55
0
55
5
55
30
60
20
10
25
65
0
0
50
65
0
60
60
10
10
55
20
50
10
10
10
70
20
15
20
50
10
0
20
5
50
65
65
10
10
15
5
55
25
55
0
25
45
50
3
7
11
15
19
23
27
31
Z
70
40
0
65
65
40
0
55
65
20
0
60
65
10
0
35
60
45
0
10
15
30
10
60
80
0
30
70
55
50
5
15
45
55
10
0
0
55
20
50
55
5
25
10
10
20
60
75
60
15
5
45
0
5
60
55
0
20
45
55
65
20
10
45
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
60
0
45
15
15
0
40
60
20
5
50
55
20
0
20
5
10
55
25
55
20
50
20
55
40
70
0
65
15
60
30
60
№ варианта
70
45
0
20
60
45
5
70
80
45
0
10
70
50
0
60
65
40
0
70
60
45
5
75
75
35
0
65
75
0
35
75
№ варианта
№ варианта
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
10
20
60
70
60
15
5
45
25
5
60
55
0
20
45
55
45
55
10
0
0
55
20
50
55
5
25
10
50
60
0
55
X Y
Точка
5
65
10
0
35
60
45
0
10
75
30
10
60
80
0
30
70
70
40
0
65
65
40
0
55
65
25
0
60
70
0
40
60
X Y Z
Точка
1
X Y Z
Точка
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
№ варианта
Точка
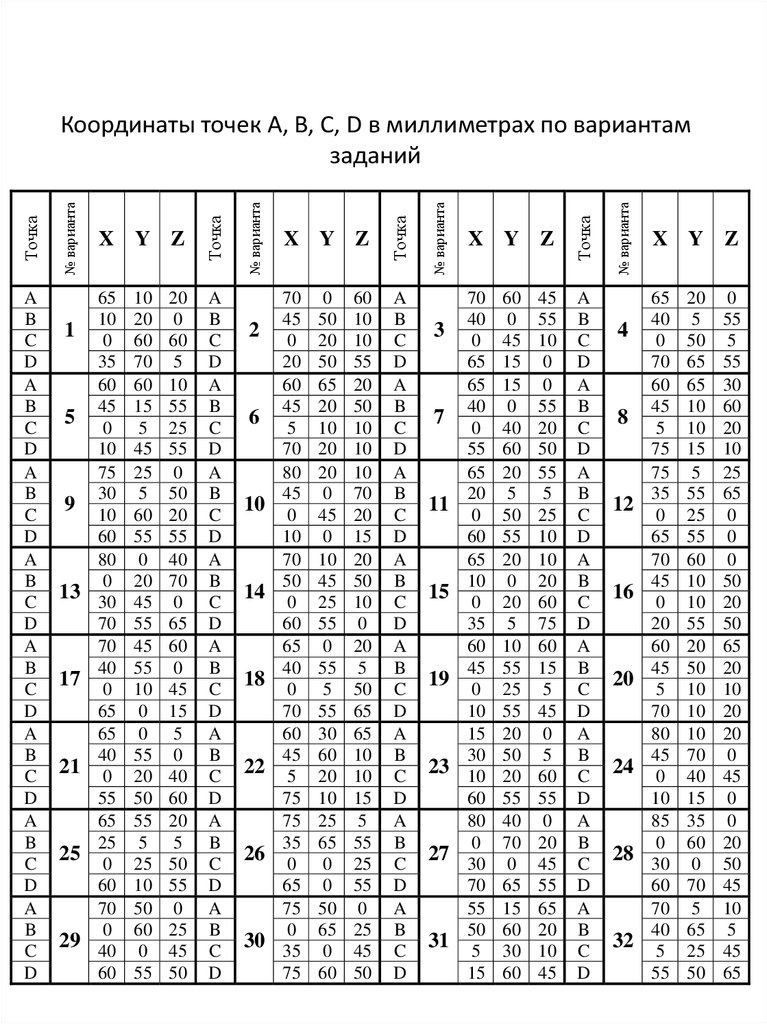
Координаты точек A, B, C, D в миллиметрах по вариантам
заданий
4
8
12
16
20
24
28
32
X Y
Z
65
40
0
70
60
45
5
75
75
35
0
65
70
45
0
20
60
45
5
70
80
45
0
10
85
0
30
60
70
40
5
55
0
55
5
55
30
60
20
10
25
65
0
0
0
50
20
50
65
20
10
20
20
0
45
0
0
20
50
45
10
5
45
65
20
5
50
65
65
10
10
15
5
55
25
55
60
10
10
55
20
50
10
10
10
70
40
15
35
60
0
70
5
65
25
50
3.
Откладываем координатные оси X, Y, Z4.
По оси X откладываем координаты X т. А5.
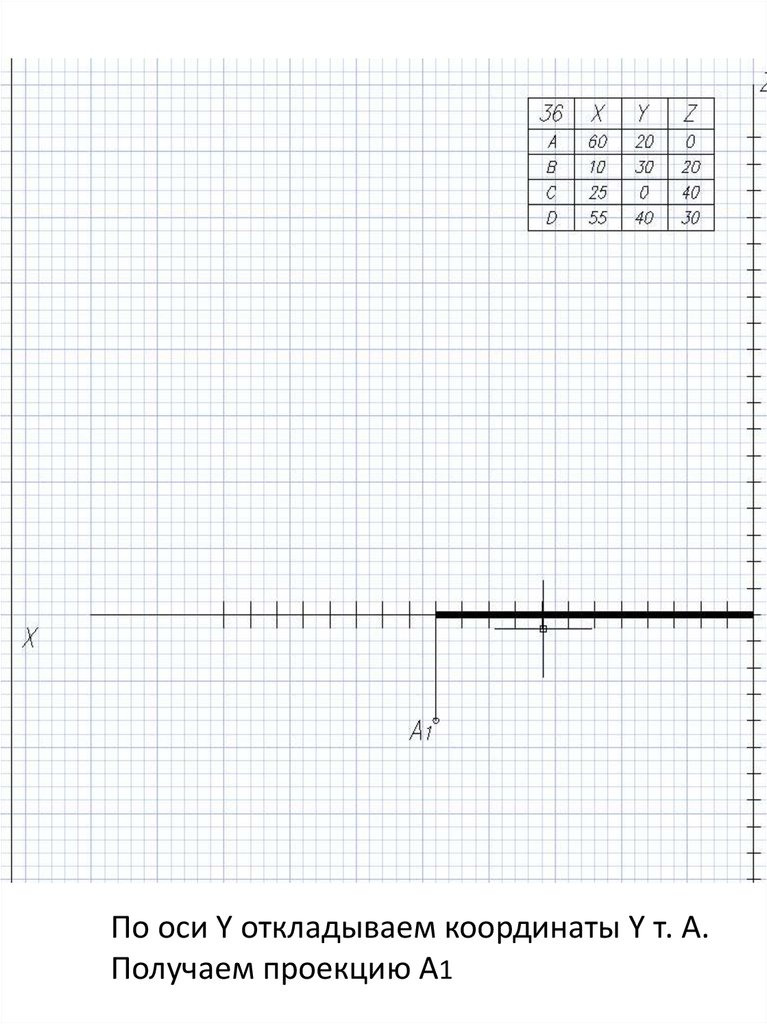
По оси Y откладываем координаты Y т. А.Получаем проекцию А1
6.
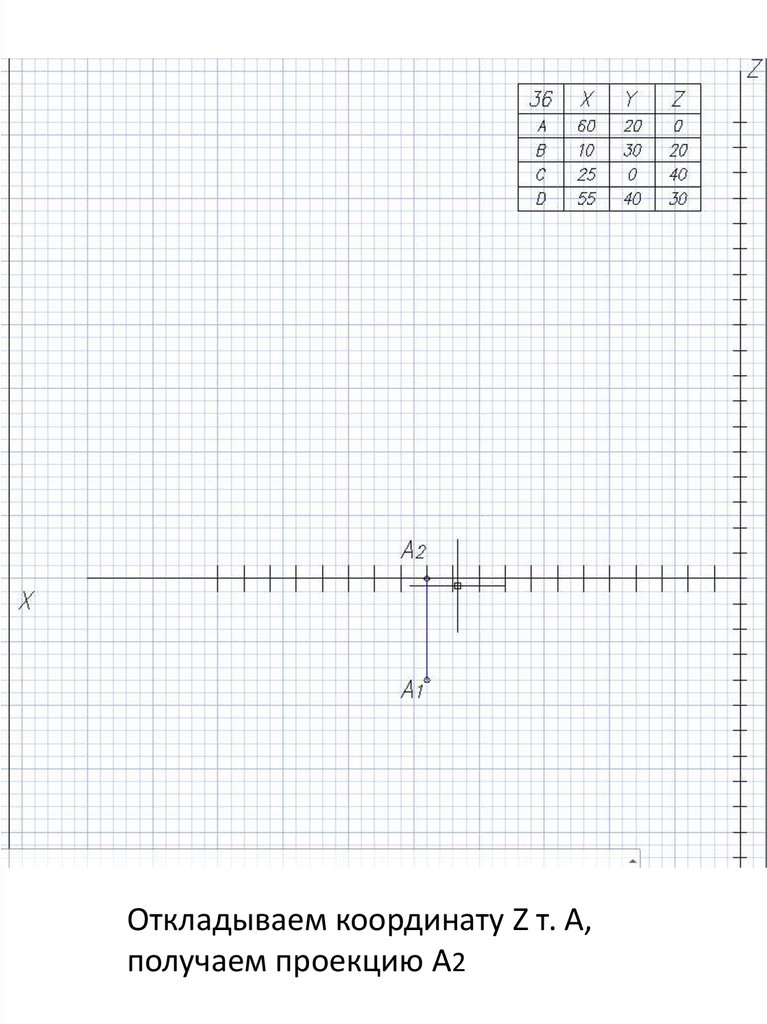
Откладываем координату Z т. А,получаем проекцию А2
7.
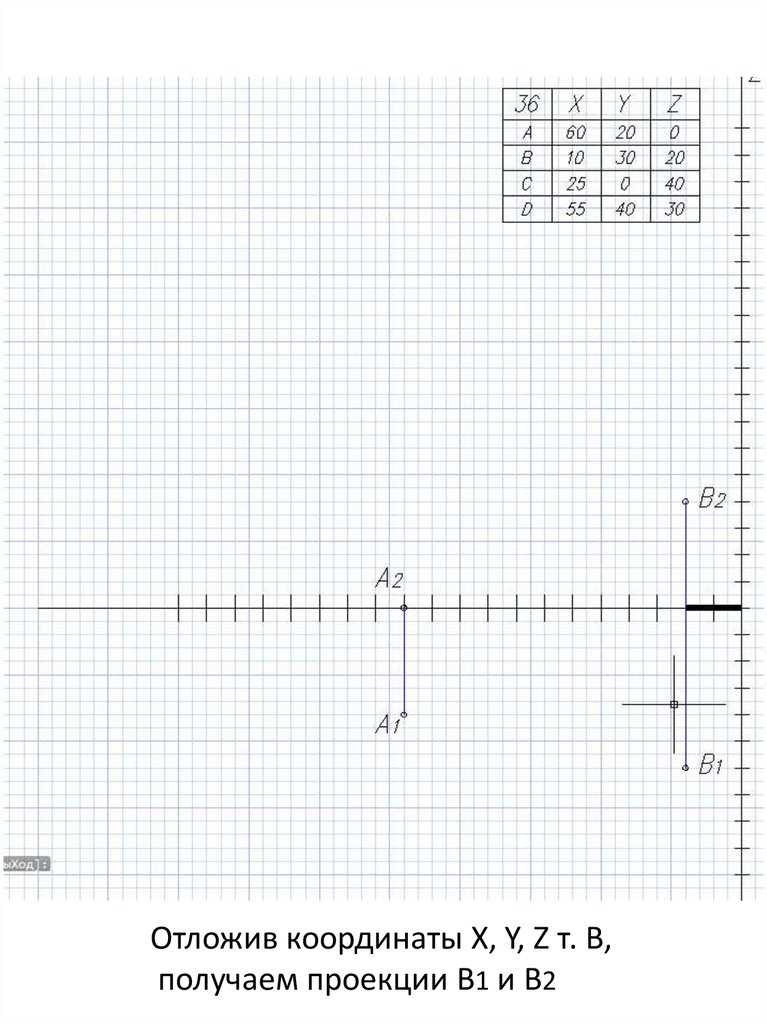
Отложив координаты X, Y, Z т. В,получаем проекции В1 и В2
8.
Аналогично получаем проекции С1 и С2 т. С9.
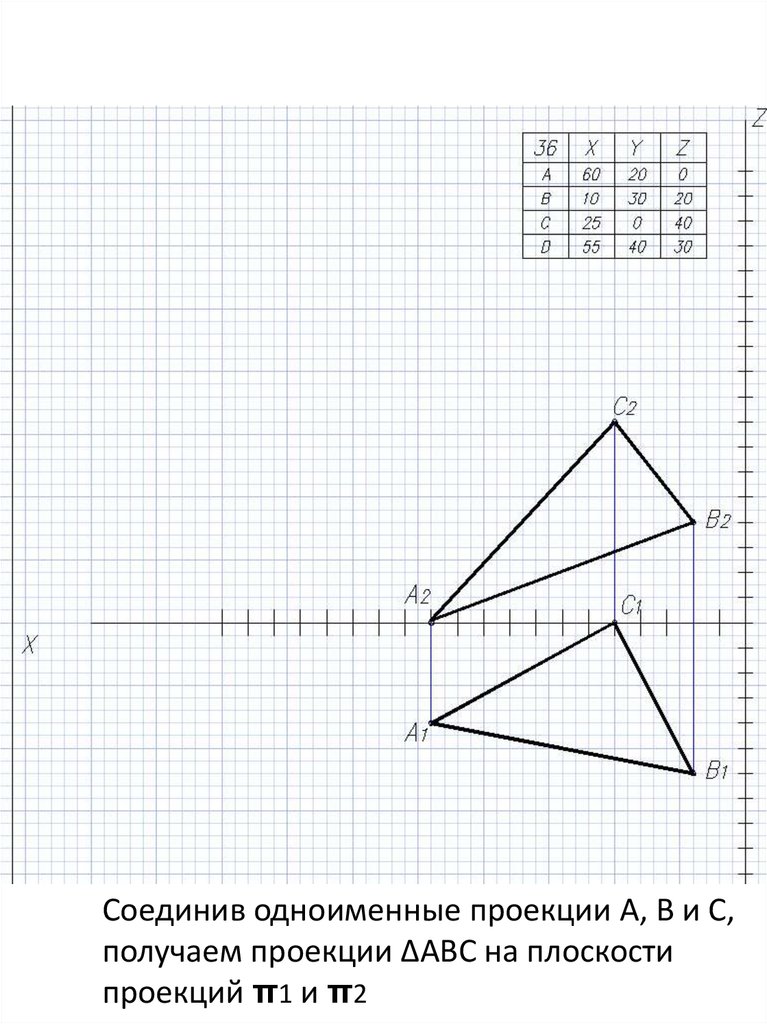
Соединив одноименные проекции А, В и С,получаем проекции ∆АВС на плоскости
проекций π1 и π2
10.
Отложив координаты X, Y, Z т. D,получаем проекции D1 и D2
11.
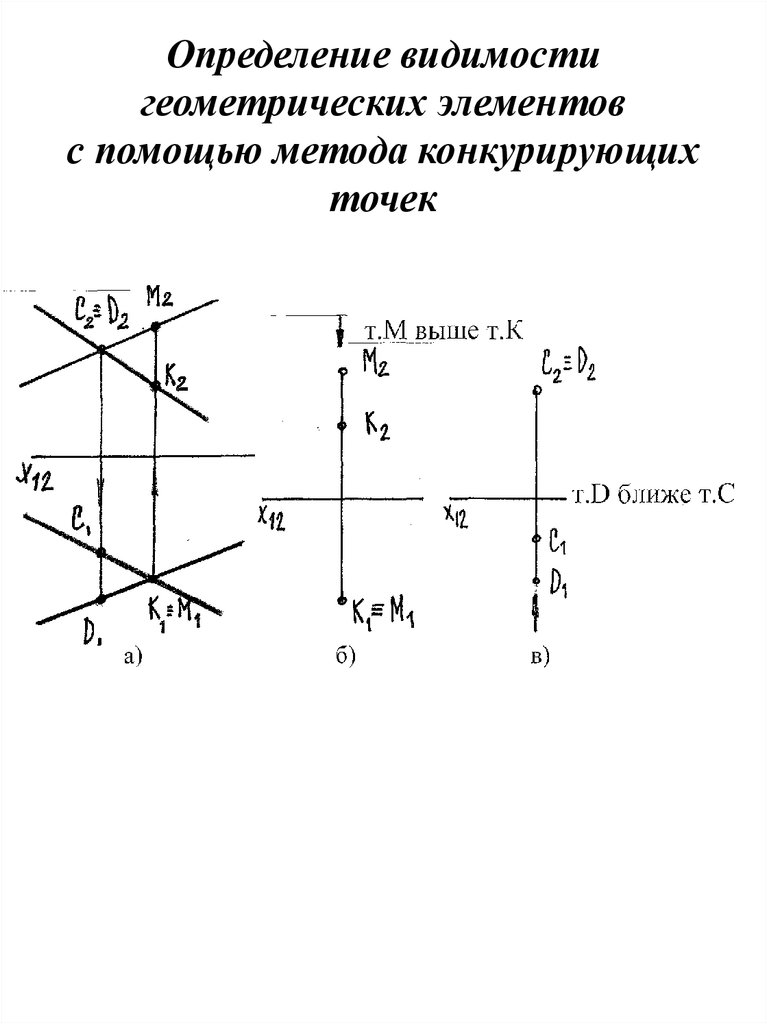
Прямая перпендикулярна плоскости, если онаперпендикулярна двум пересекающимся
прямым этой плоскости. Для того чтобы
прямые углы спроецировались в натуральную
величину, один из лучей должен быть
горизонталью и фронталью. В ∆АВС строим
горизонталь плоскости (h2‖оси X)
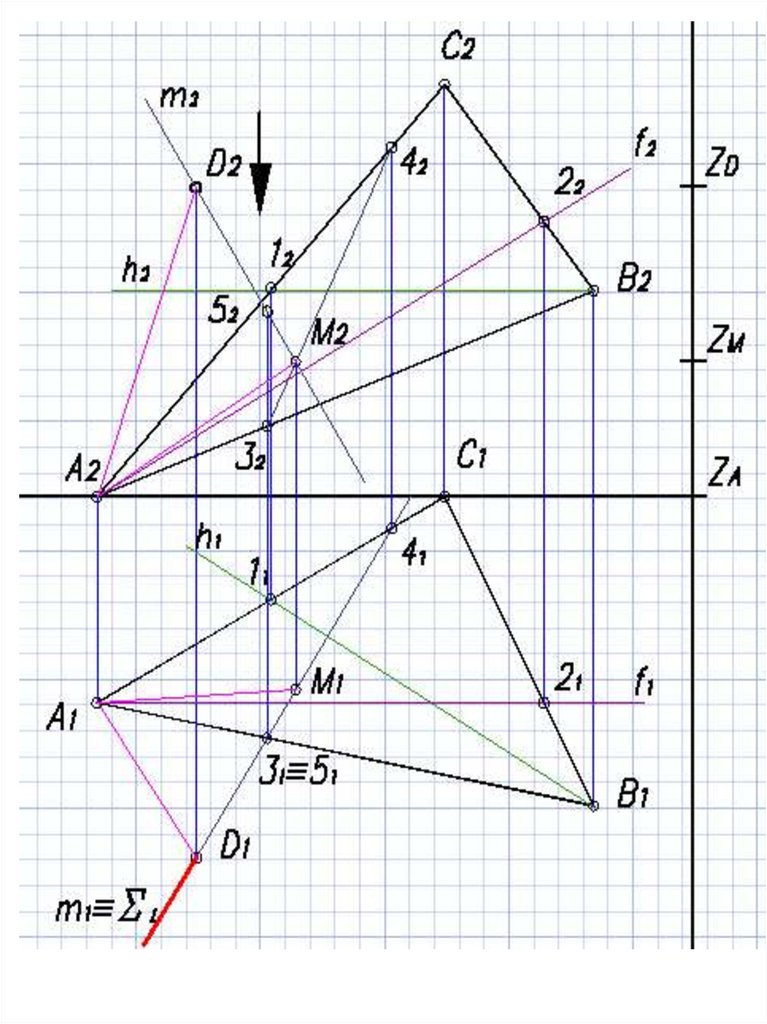
12.
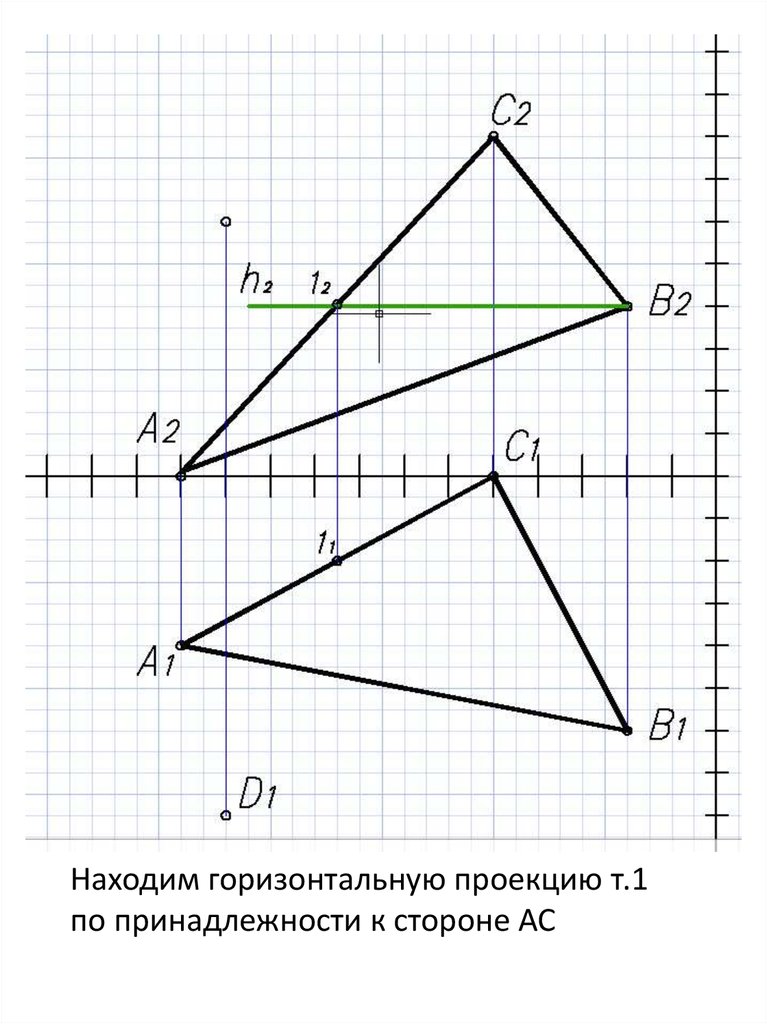
Находим горизонтальную проекцию т.1по принадлежности к стороне АС
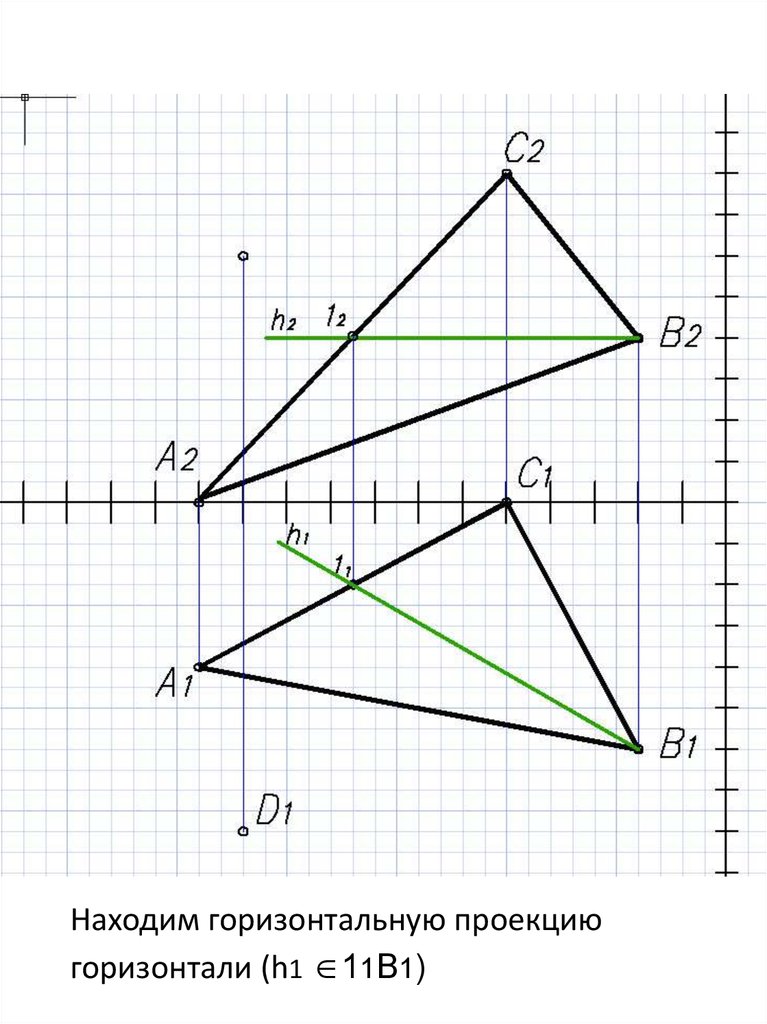
13.
Находим горизонтальную проекциюгоризонтали (h1 11В1)
14.
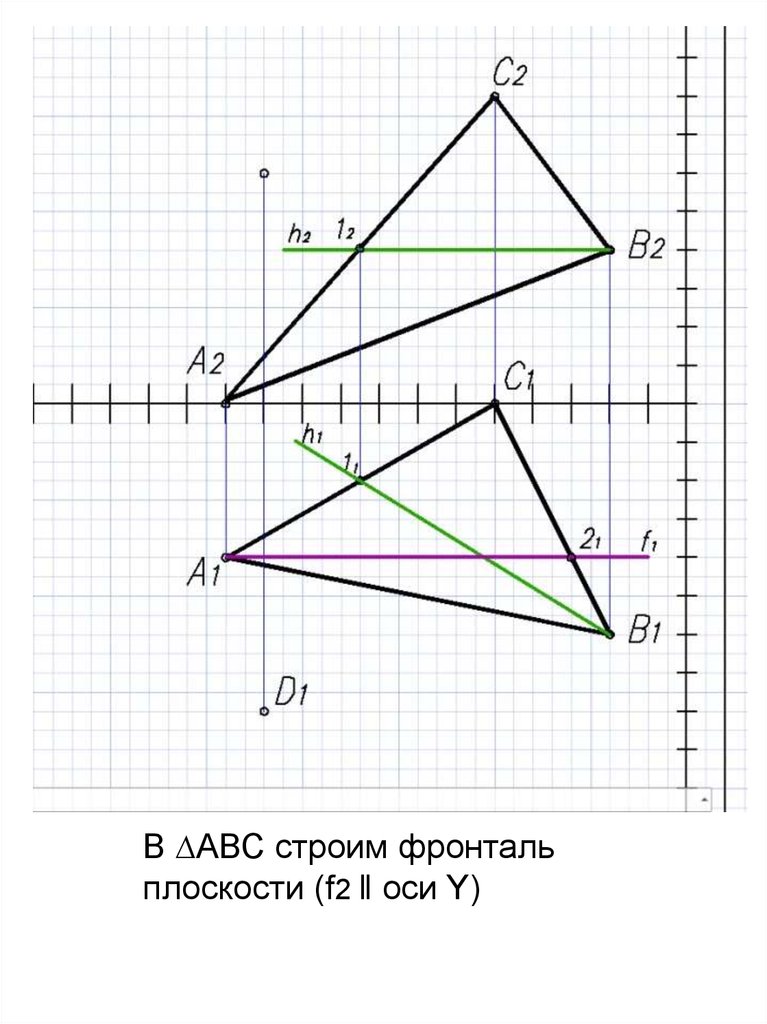
В ∆АВС строим фронтальплоскости (f2 ‖ оси Y)
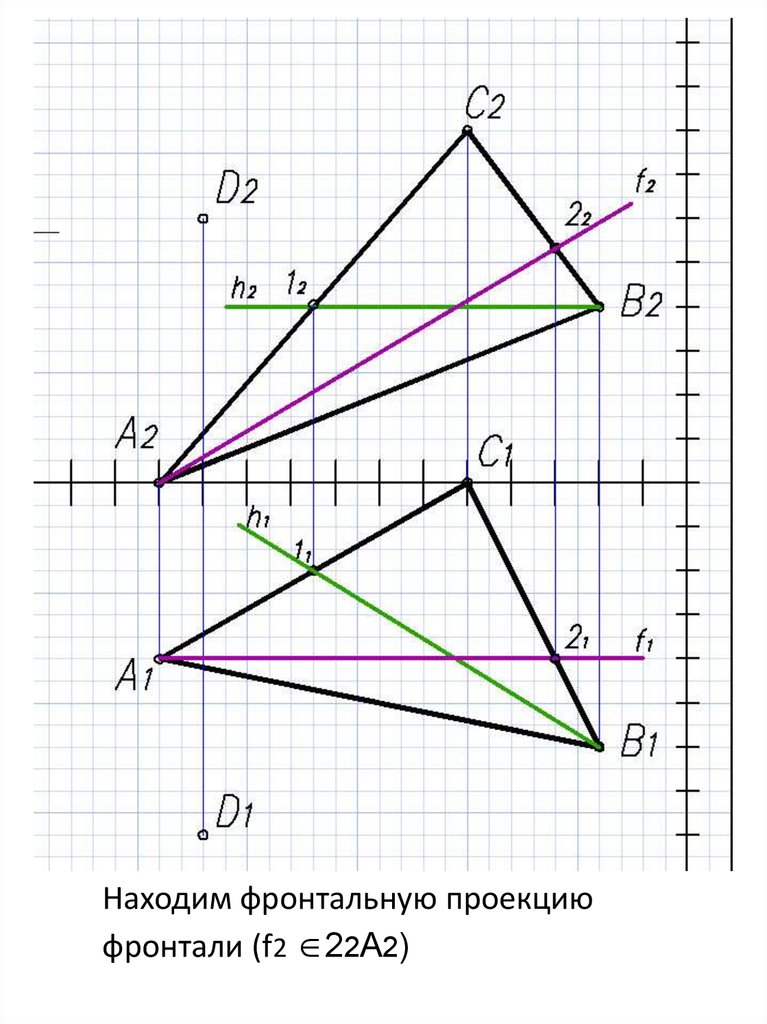
15.
Находим фронтальную проекциюфронтали (f2 22A2)
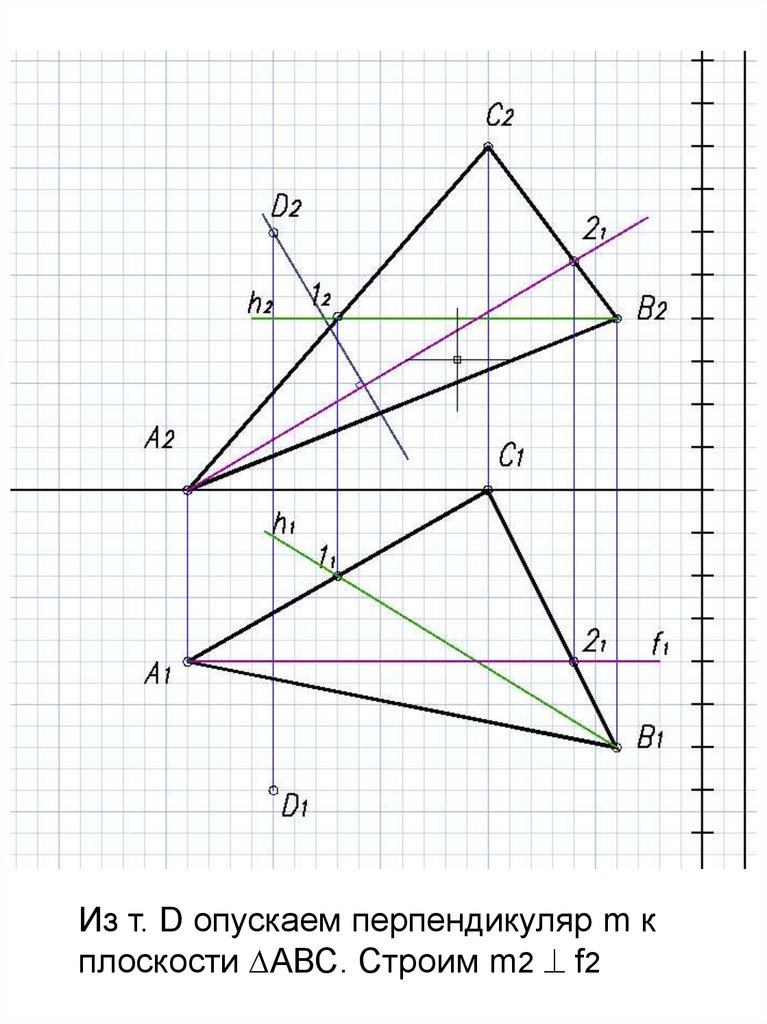
16.
Из т. D опускаем перпендикуляр m кплоскости ∆АВС. Строим m2 f2
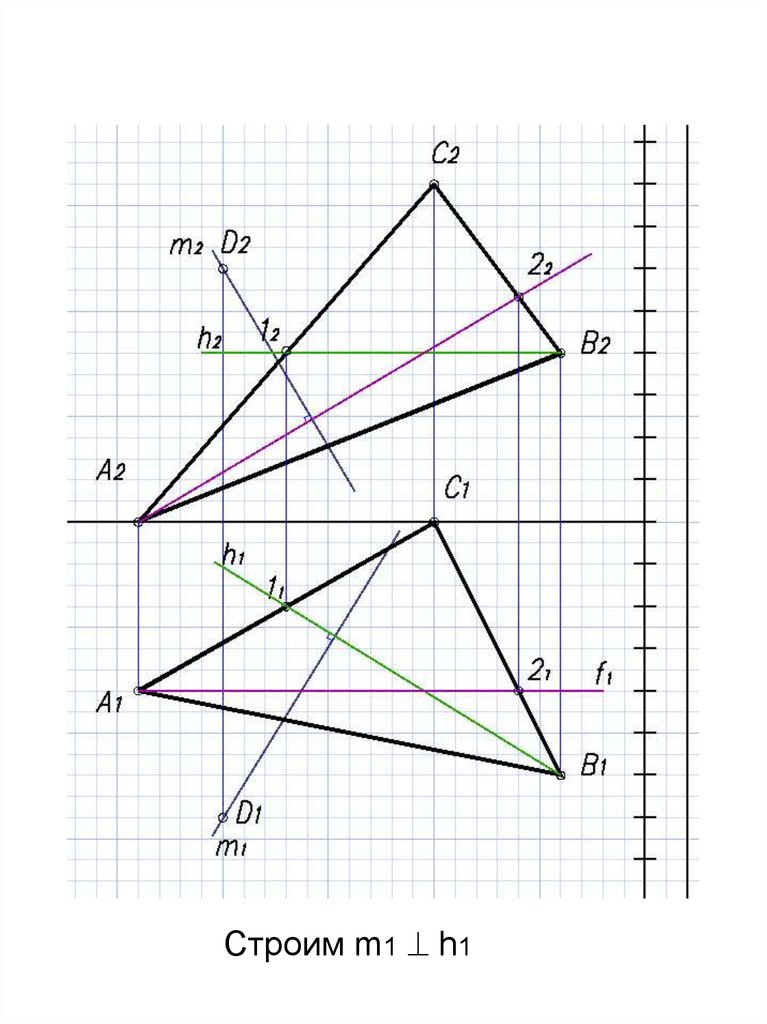
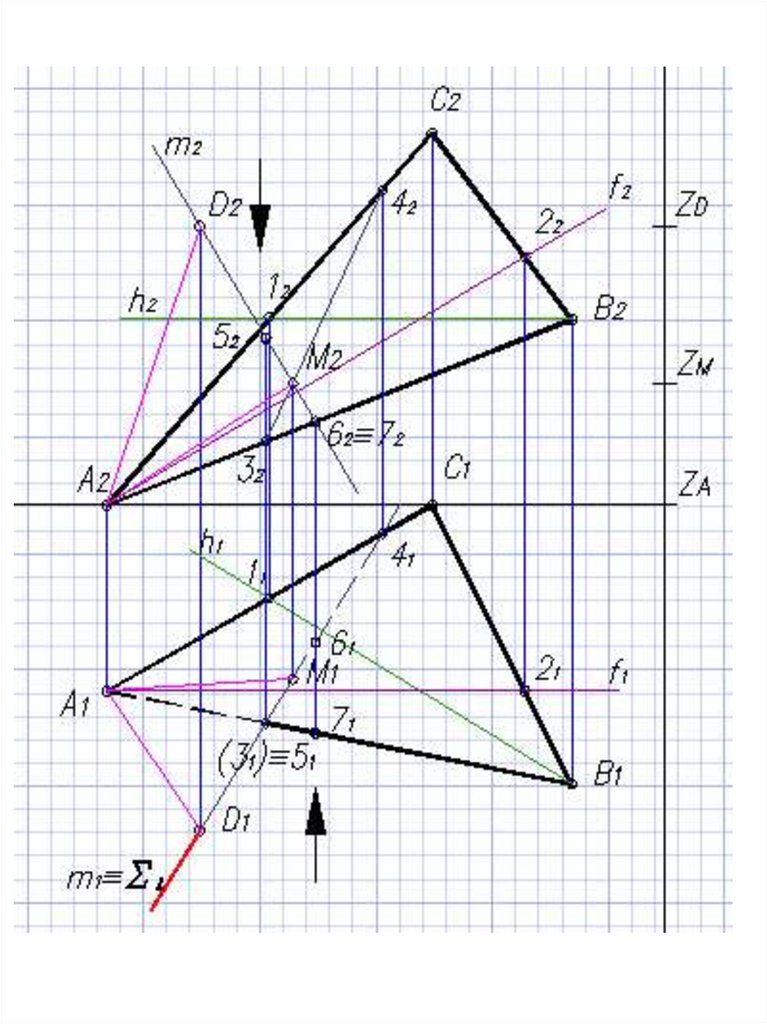
17.
Строим m1 h118.
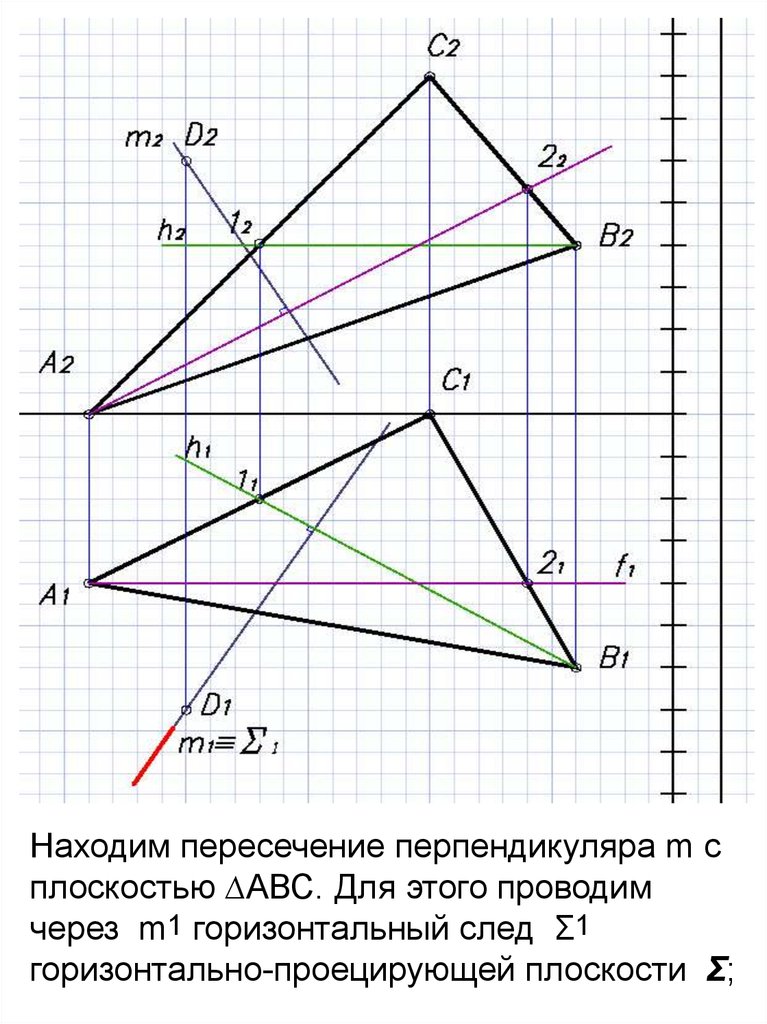
Находим пересечение перпендикуляра m cплоскостью ∆АВС. Для этого проводим
через m1 горизонтальный след Σ1
горизонтально-проецирующей плоскости Σ;
19.
Находим линию 3 4 пересечениявспомогательной плоскости с плоскостью
∆АВС
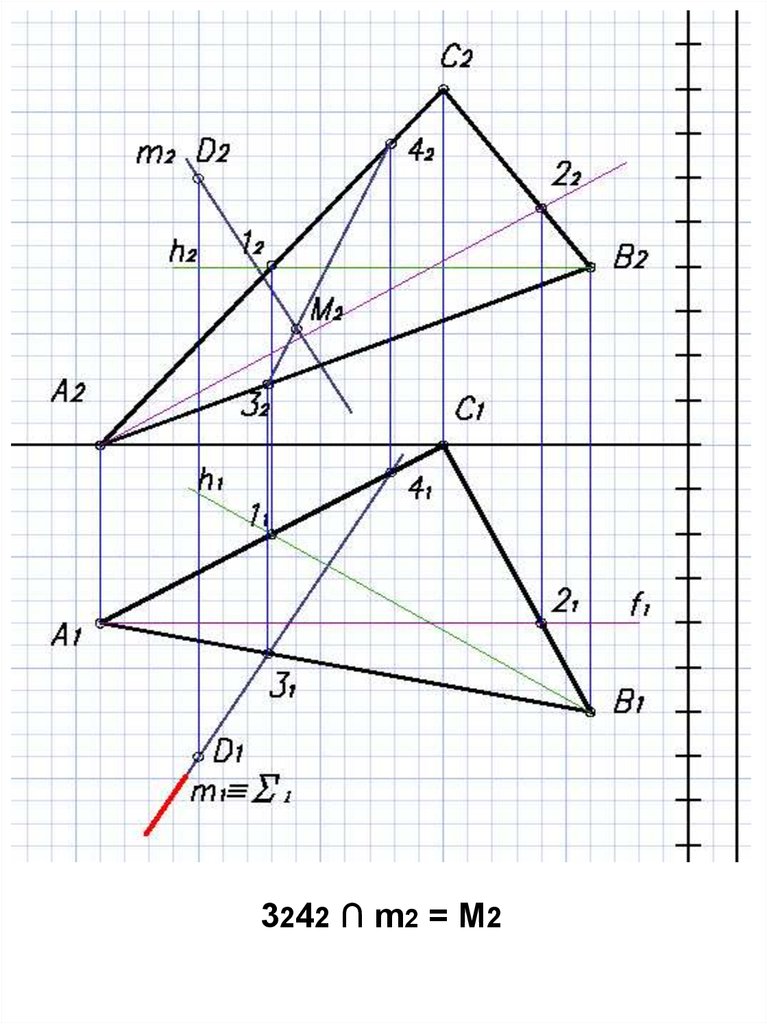
20.
21.
3242 ∩ m2 = M222.
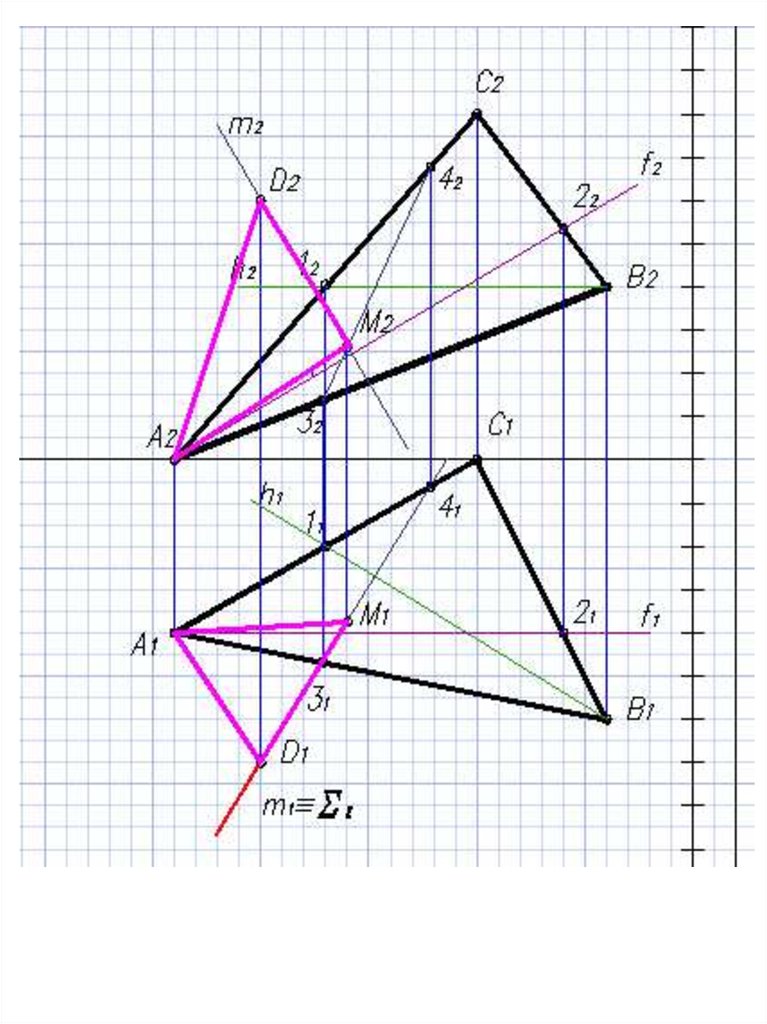
M1 m123.
АМ – проекция ребра AD на плоскость ∆АВС24.
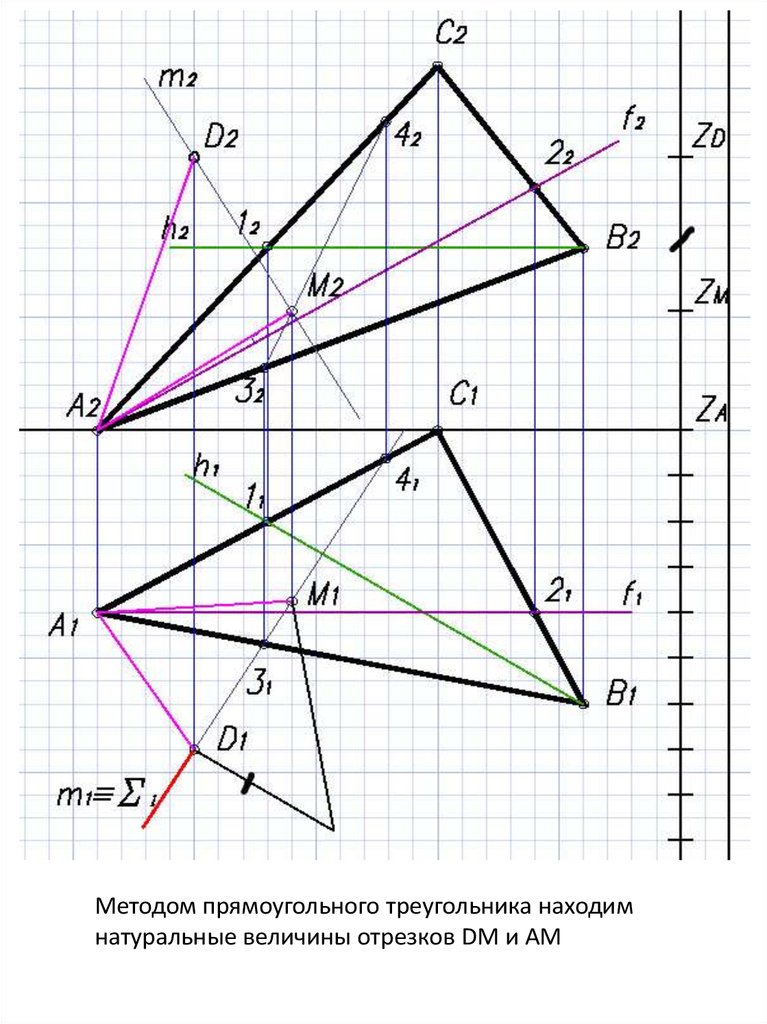
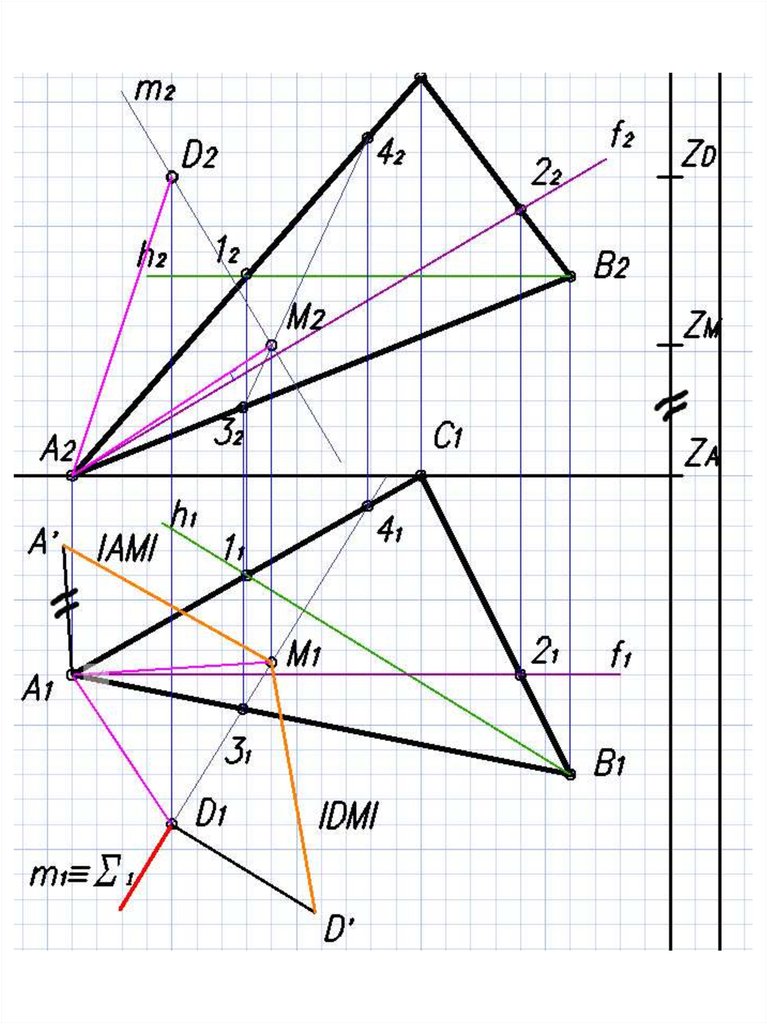
25.
Методом прямоугольного треугольника находимнатуральные величины отрезков DM и AM














 mathematics
mathematics








