Similar presentations:
Прямая на плоскости
1.
Прямая на плоскости.2.
Прямая на плоскости.1.Теоретическая часть
2.Задачи
3.Решения задач
Оглавление
3.
Прямая на плоскости.1.Простейшие задачи на плоскости
1.1 Расстояние между двумя точками
1.2 Деление отрезка в данном отношении
2. Прямая линия на плоскости
2.1 Общее уравнение прямой
2.2 Каноническое уравнение прямой
2.3 Уравнение прямой, проходящей через две точки
2.4 Уравнение прямой, проходящей через данную точку в заданном направлении
2.5 Уравнение прямой в отрезках
2.6 Нормальное уравнение прямой
2. 7 Расстояние от точки до прямой
2.8 Координаты точки пересечения двух прямых
2.9 Угол между двумя прямыми
2.10 Условие параллельности и перпендикулярности двух прямых
2.11 Уравнение пучка прямых
3.Основные формулы
4.
Прямая на плоскости.Оглавление:
1.ПРОСТЕЙШИЕ ЗАДАЧИ НА ПЛОСКОСТИ
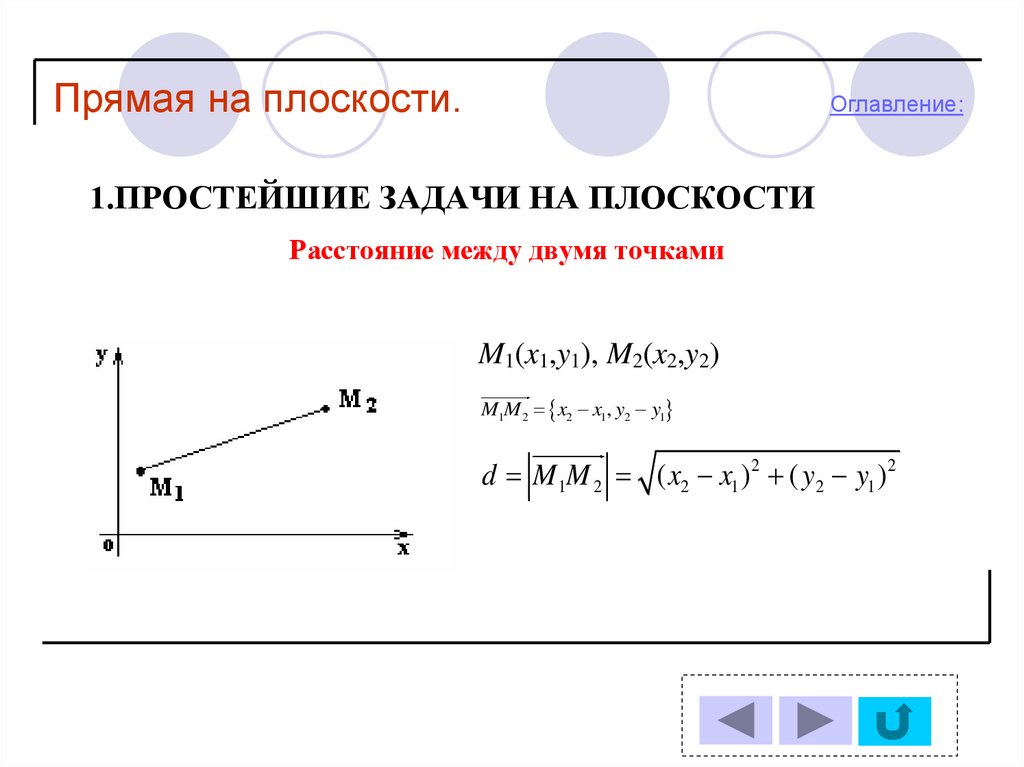
Расстояние между двумя точками
M1(x1,y1), M2(x2,y2)
M1M 2 x2 x1, y2 y1
d M 1M 2 ( x2 x1 ) 2 ( y2 y1 ) 2
5.
Прямая на плоскости.Оглавление:
Деление отрезка в данном отношении
Точка M(x,y) делит отрезок M1M2 в отношении
M 1M
MM 2
:
x x1 y y1
, M1M MM 2 , x x y y ,
2
2
координаты точки М находятся по формулам:
x1 x2
x
1
y y1 y2
1
.
6.
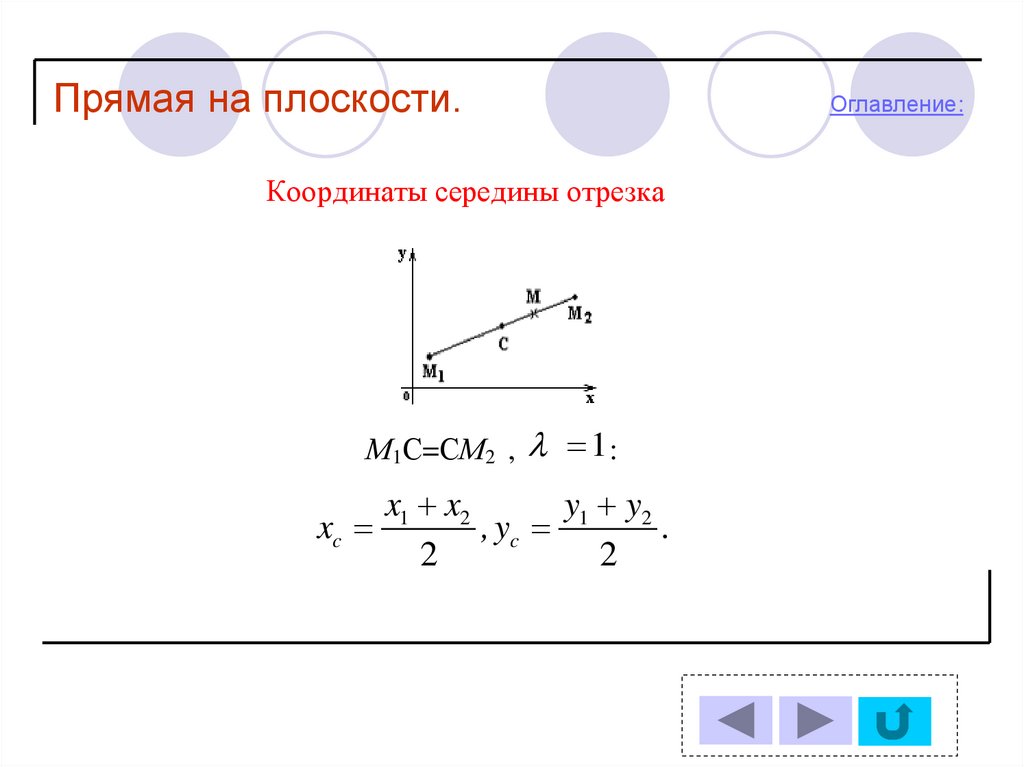
Прямая на плоскости.Координаты середины отрезка
М1С=СМ2 , 1 :
x1 x2
y1 y2
xc
, yc
.
2
2
Оглавление:
7.
Прямая на плоскости.Оглавление:
2.ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
Общее уравнение прямой
Общее уравнение прямой на плоскости XOY получается из общего
уравнения плоскости в пространстве при z = 0.
L: Ax+By+C=0.
А = 0 (В = 0) L OX ( OY);
С=0 0 , 0 L .
Уравнение прямой, проходящей через точку М(x0,y0) перпендикулярно
вектору n A, B , принимает вид:
A( x x0 ) B( y y0 ) 0 .
8.
Прямая на плоскости.Канонические и параметрические уравнения прямой
Уравнения прямой, проходящей через точку М (x0,y0)
a
параллельно направляющему вектору {l,m} :
x x0 y y0
l
m
x x0 lt ,
t ( , ).
y y0 mt ,
Оглавление:
9.
Прямая на плоскости.Оглавление:
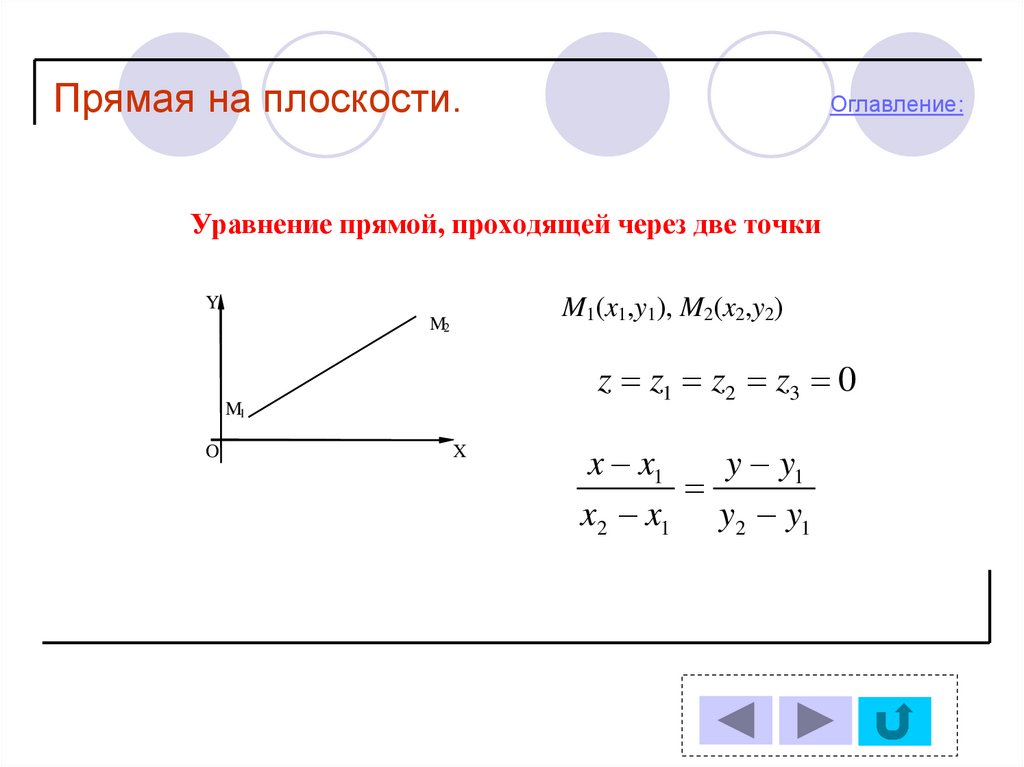
Уравнение прямой, проходящей через две точки
Y
M1(x1,y1), M2(x2,y2)
M2
z z1 z2 z3 0
M1
O
X
x x1
y y1
x2 x1 y2 y1
10.
Прямая на плоскости.Оглавление:
Уравнение прямой, проходящей через данную точку в заданном направлении
Прямая составляет угол с осью OX.
Угловым коэффициентом прямой
называется число k tg .
Из общего уравнения прямой
Ax+By+C=0, B 0
А b C
k
,
y k x b,
B.
B
Прямая пересекает ось OY в точке (0,b).
11.
Прямая на плоскости.Оглавление:
Уравнение прямой, проходящей через данную точку в заданном направлении
Прямая задана двумя точками М1(x1,y1) и
М2(x2,y2).
Из уравнения прямой, проходящей через две
точки, имеем
y2 y1
( x x1 ).
y y1
x2 x1
y2 y1
tg k .
x2 x1
y y1 k ( x x1 ).
12.
Прямая на плоскости.Оглавление:
Уравнение прямой в отрезках
Общее уравнение прямой Ax+By+C=0 может быть преобразовано
x
y
x y
1,
1
С
к виду уравнения прямой «в отрезках»: С
.
a
b
А
В
Прямая в отрезках пересекает ось OX в точке А(а,0) и ось OY в
точке В(0,b).
13.
Прямая на плоскости.Оглавление:
Нормальное уравнение прямой
Из нормального уравнения плоскости в пространстве, полагая z =
0 и учитывая, что
cos( ) sin ,
2
получаем нормальное уравнение прямой на плоскости в виде:
x cos y sin p 0 .
Здесь OP p - расстояние от прямой до начала координат,
- угол между перпендикуляром к прямой и осью OX.
14.
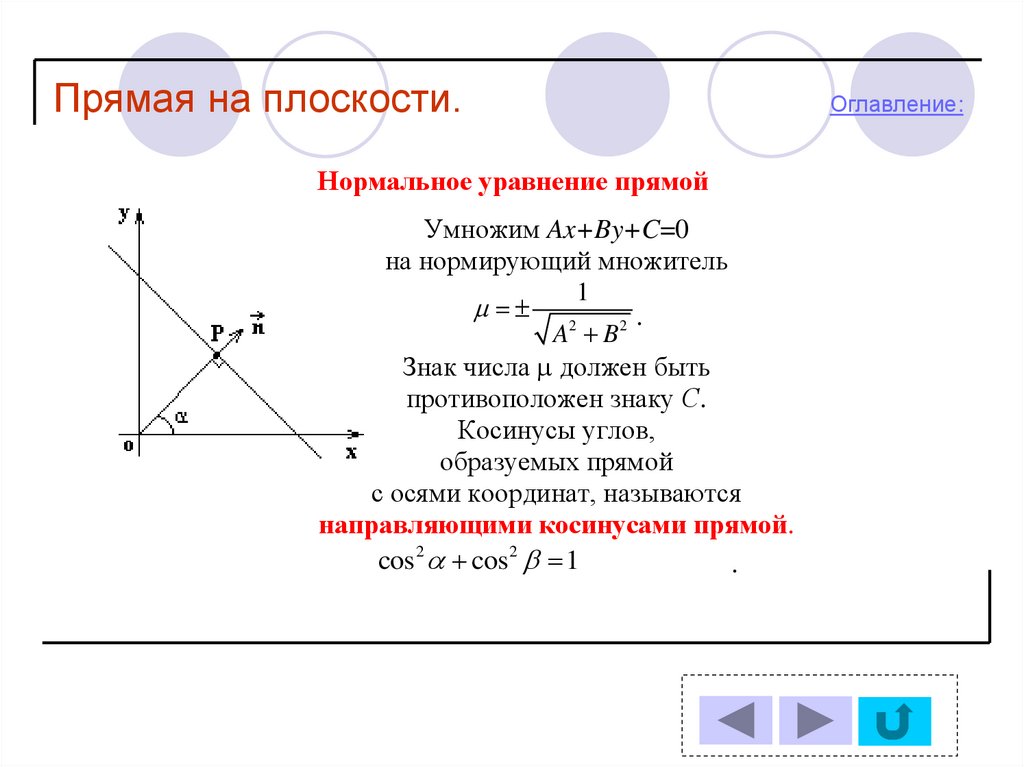
Прямая на плоскости.Нормальное уравнение прямой
Умножим Ax+By+C=0
на нормирующий множитель
1
2
.
A B2
Знак числа должен быть
противоположен знаку С.
Косинусы углов,
образуемых прямой
с осями координат, называются
направляющими косинусами прямой.
cos2 cos2 1
.
Оглавление:
15.
Прямая на плоскости.Оглавление:
Расстояние от точки до прямой
Расстояние d от точки M0(x0,y0) до прямой L: Ax+By+C=0,
x cos y sin p 0 :
M o , L d x0 cos y0 sin p
Ax0 By0 C
A B
2
2
.
>0 - точка М0 и начало координат лежат по разные стороны от
прямой, в противном случае <0.
16.
Прямая на плоскости.Оглавление:
Координаты точки пересечения двух прямых
L1 A1 x B1 y C1 0,
x0 , y0
,
L2 A2 x B2 y C2 0
B1
x0
C1
C1
B2 C2
C
, y0 2
A1 B1
A1
À2
B2
A2
A1
A2
A1
,
B1 по формулам Крамера, если A
2
B2
B1
B2
0.
17.
Прямая на плоскости.Оглавление:
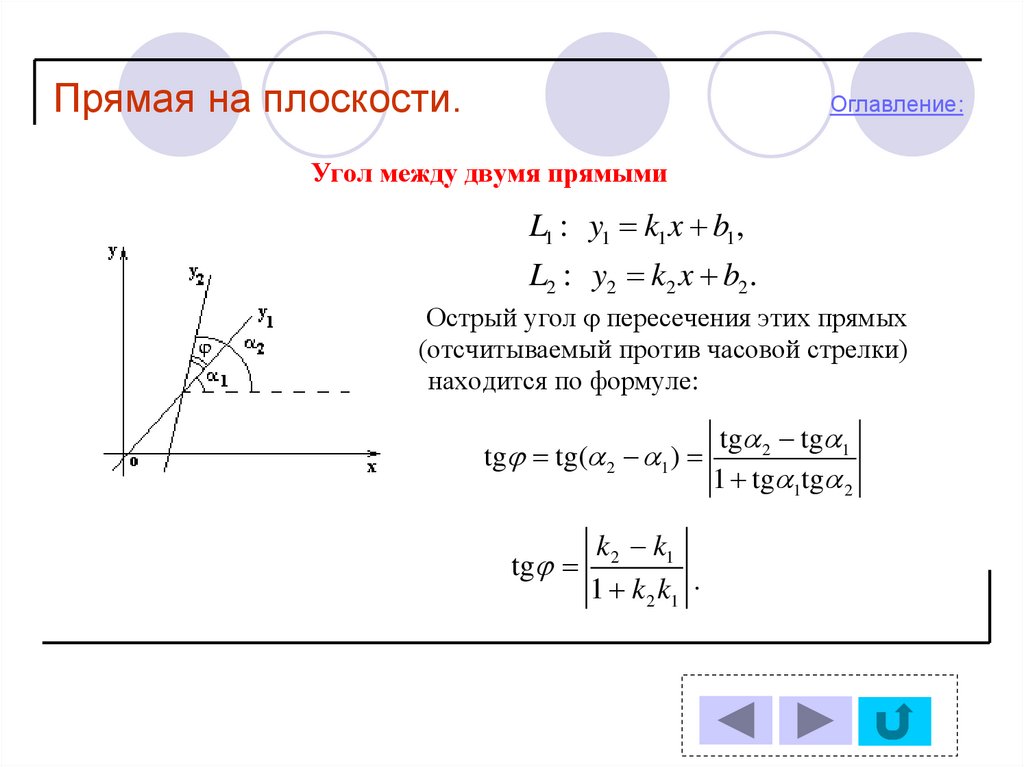
Угол между двумя прямыми
L1 : y1 k1 x b1 ,
L2 : y2 k2 x b2 .
Острый угол пересечения этих прямых
(отсчитываемый против часовой стрелки)
находится по формуле:
tg tg( 2 1 )
k2 k1
tg
1 k2 k1 .
tg 2 tg 1
1 tg 1tg 2
18.
Прямая на плоскости.L1 : А1 x + B1 y + C1=0, L2 : A2 x + B2 y + C2=0,
A
A
tg 1 1 , tg 2 2 ,
B1
B2
угол между прямыми определяется формулой:
A1B2 A2 B1
tg
.
A1 A2 B1B2
Оглавление:
19.
Прямая на плоскости.Оглавление:
Условие параллельности и перпендикулярности двух
прямых
L1 : y1 k1 x b1 , L2 : y2 k2 x b2 .
L1 L2
L1 L2
k1=k2
k1k2 = -1
tg
( 0 ,
(
2
, tg
k2 k1
0)
1 k2 k1
k2 k1
)
1 k2 k1
k1
1
k2
.
L1
L1
L1 : А1 x + B1 y + C1=0, L2 : A2 x + B2 y + C2=0:
A1 A2
L А1В1 – А2В1=0,
B1 B2 ,
L А1А2+В1В2=0.
2
2
20.
Прямая на плоскости.Оглавление:
Уравнение пучка прямых
Совокупность всех прямых плоскости, проходящих через
некоторую точку M o (x0,y0), называется пучком прямых с центром M o .
Если A1x+B1y+C1=0 и A2x+B2y+C2=0 - уравнения двух прямых,
уравнение
то
точке
в
пересекающихся
Mo ;
A1x+B1y+C1+ (A2x+B2y+C2)=0 определяет все прямые пучка, кроме
второй из прямых.
21.
Прямая на плоскости.Оглавление:
3.ОСНОВНЫЕ ФОРМУЛЫ
d
( x2 x1 ) 2 ( y2 y1 ) 2
x1 x2
x
,
1
y y1 y2 ,
1
1
x1 x2
;
2
y y2
y 1
2
x
-расстояние между точками A(x1,y1) и
B(x2,y2);
-координаты точки С(x,y), которая
делит отрезок, соединяющий точки
A(x1,y1) и B(x2,y2), в отношении
AC
CB ;
-координаты середины отрезка АВ;
22.
Прямая на плоскости.x1
y1 1
x2
y2 1 0
x3
y3 1
x1
1
S x2
2
x3
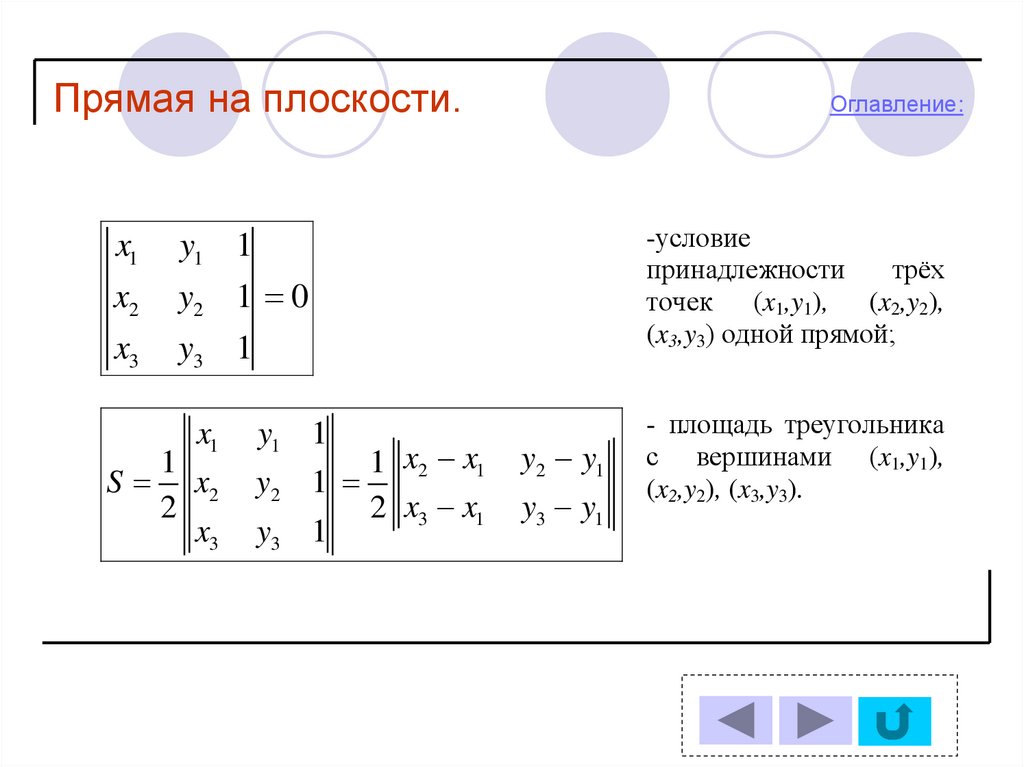
-условие
принадлежности
трёх
точек (x1,y1), (x2,y2),
(x3,y3) одной прямой;
y1 1
y2
y3
Оглавление:
1 x2 x1
1
2 x3 x1
1
y2 y1
y3 y1
- площадь треугольника
с вершинами (x1,y1),
(x2,y2), (x3,y3).
23.
Прямая на плоскости.Ax+By+C=0
A(x-x0)+B(y-y0)=0
x x0 y y0
l
m
Оглавление:
- общее уравнение прямой;
- уравнение прямой, проходящей через
точку (x0,y0) перпендикулярно
нормальному вектору {A,B};
- каноническое уравнение прямой,
проходящей
через
точку
(x0,y0)
параллельно вектору {l,m};
24.
Прямая на плоскости.x x0 lt,
y y0 mt,
t ( , )
Оглавление:
параметрические
уравнения
прямой,
проходящей через точку (x0,y0) параллельно
вектору l,m ;
y y1
x x1
y2 y1 x2 x1
- уравнение прямой, проходящей через две
заданные точки (x1,y1) и (x2,y2);
y kx b,
- уравнение прямой с угловым коэффициентом
k tg
k, где 0, 2 2 , - угол наклона прямой к
оси ox;
25.
Прямая на плоскости.Оглавление:
- уравнение прямой в отрезках, где (а,0) и
(0,b) - координаты точек пересечения
прямой с осями ox и oy;
x y
1,
a b
a 0, b 0
x cos y sin p 0 - нормальное уравнение прямой, где р расстояние от начала координат до прямой,
-угол между осью ox и перпендикуляром к
прямой,
проходящем
через
начало
координат;
Ax By C
A B
2
2
0
- нормальный вид общего уравнения
прямой; знак нормирующего множителя
противоположен знаку С;
26.
Прямая на плоскости.d
x
0
y0
Ax0 By0 C
A2 B 2
B1
C1
B2
A1
C2
,
B1
A2
B2
C1
A1
C2
A1
A2
B1
A2
B2
b2 b1
x0 k k ,
1
2
y b2 k1 b1k 2
0
k1 k 2
Оглавление:
- расстояние от точки (x0,y0) до прямой
Ax+By+C=0;
- координаты точек пересечения двух прямых
A1x+B1y+C1=0 и A2x+B2y+C2=0;
- координаты точек
y=k1x+b1 и y=k2x+b2;
пересечения
прямых
27.
Прямая на плоскости.A1 B2 A2 B1 0,
k1 k 2
A1 A2 B1 B2 0,
k1k 2 1
Оглавление:
- условия параллельности прямых, заданных в
общем виде
A1x+B1y+C1=0, A2x+B2y+C2=0
и в виде y=k1x+b1, y=k2x+b2 ;
- условие перпендикулярности прямых,
заданных в общем виде
A1x+B1y+C1=0, A2x+B2y+C2=0
и в виде y=k1x+b1, y=k2x+b2 ;
28.
Прямая на плоскости.A B A2 B1
tg 1 2
,
A1 A2 B1 B2
tg
k1 k 2
,
1 k1 k 2
Оглавление:
- угол между двумя прямыми, заданными в
общем виде
A1x+B1y+C1=0, A2x+B2y+C2=0
и в виде y=k1x+b1, y=k2x+b2 ;
k1 k 2 1,
2
, если k1 k 2 1.
A1x+B1y+C1+
+ (A2x+B2y+C2)=0
- уравнение пучка прямых через точку М, если
A1x+B1y+C1=0 и A2x+B2y+C2=0 - уравнения двух
прямых, пересекающихся в точке М.
29.
Прямая на плоскости.Задача №:
1
2
3
4
5
6
Оглавление:
30.
Прямая на плоскости.Решение задачи №:
Оглавление:
1а
2
1б
3
1в
4
1г
5
1д
6
1ж
1з
1и
1к
1л
31.
Прямая на плоскости.Оглавление:
Треугольник задан уравнениями трех его сторон:
АС:
х – 2у + 5 = 0,
АВ:
х + 2у – 3 = 0,
ВС: 2х + у – 15 = 0.
Определите следующие элементы треугольника:
а) координаты вершин,
б) уравнения высот,
в) уравнения медиан,
г) длины сторон,
д) уравнения биссектрис,
ж) центр и радиус вписанной окружности,
з) центр и радиус описанной окружности,
и) центр тяжести треугольника,
к) внутренние углы треугольника,
л) площадь треугольника.
Задача 1
Ответ:
Решение:
32.
Прямая на плоскости.Оглавление:
Найдите проекцию точки Р (4, 9) на прямую,
проходящую через точки А (3, 1) и В (5, 2).
Задача 2
Ответ:
7,3
Решение:
33.
Прямая на плоскости.Оглавление:
Постройте прямую 3х – 5у + 15 = 0.
Задача 3
Ответ:
Решение:
34.
Прямая на плоскости.Оглавление:
Даны две прямые L1 : 2х + 3у – 5 = 0, L2 : 7х +15у +1 = 0,
пересекающиеся в точке М. Составьте уравнение прямой, которая
проходит через точку М перпендикулярно к прямой
L3 : 12х – 5у – 1 = 0.
Задача 4
Ответ: 5х + 12у + 6 = 0.
Решение:
35.
Прямая на плоскости.Оглавление:
Напишите уравнение прямой L, проходящей через точку М (2, 1)
под углом 45 к прямой L1: 2х + 3у +4 = 0.
Задача 5
x 5 y 3 0,
Ответ: 5 x y 11 0
Решение:
36.
Прямая на плоскости.Оглавление:
Составьте уравнение прямой L, параллельной прямым
L1: х + 2у – 1 = 0 и L2: х + 2у +2 = 0
и проходящей посередине между ними.
Задача 6
Ответ: х+2у+1/2=0
Решение:
37.
Прямая на плоскости.Оглавление:
а) Координаты вершин треугольника находятся как точки пересечения
соответствующих сторон:
AC : x 2 y 5 0,
А (-1, 2).
AB : x 2 y 3 0,
Аналогично В (9, -3) и С (5, 5).
Решение задачи 1
Ответ: а) А (-1, 2),В (9, -3),С (5, 5)
38.
Прямая на плоскости.Оглавление:
б) Высотой треугольника называется отрезок перпендикуляра, опущенного из вершины
треугольника на противоположную сторону.
hc = CC1 AB, СС1 :у = k1x + b,
1
3
y
x
,
АВ:
2
2
1
k2 .
2
k1 k2= - 1 k1=2.
С (5, 5) СС1 , hc : у – 5 = 2 (х – 5), у = 2х – 5.
1
5
y
x
АС:
2
2 , ВС: у = -2х + 5 АС ВС,
треугольник является прямоугольным,
1
5
hA: y 2 x 2 ; hB: у = -2х + 15.
Решение задачи 1
1
5
y
x
2
2
Ответ: б)
у= - 2х+15
у=2х–5
39.
Прямая на плоскости.Оглавление:
Медианой называется отрезок прямой, соединяющей
вершину треугольника с серединой противолежащей
стороны.
Координаты середин сторон:
С2 (4, -1/2), В2 (2, 7/2), А2 (7, 1).
mC = CC2, С mC , С2 mC:
в)
y 5
x 5
mC: 1 2 5 4 5
11х–2у–45=0.
г) Длины сторон:
AB c 102 52 5 5,
Аналогично mВ: 13х+14у–75=0,
mА: x+8y–15=0.
BC a 4 5,
AC b 3 5.
Ответ:
в) x+8y–15=0,
13х+14у–75=0 ,11х–2у–45=0
Решение задачи 1
5 5,
г)
4 5,
3 5
40.
Прямая на плоскости.Оглавление:
д) Биссектрисой треугольника называется лежащий в треугольнике
отрезок прямой, которая делит его внутренний угол пополам.
1-ый способ. Биссектриса делит противолежащую сторону в
отношении, пропорциональном прилежащим сторонам.
Если С3 – точка пересечения биссектрисы lC = CC3 со стороной АС, то
АС3 АС b 3
.
С3 В СВ a 4
Координаты точки С3 находим по формулам деления отрезка в
отношении = 3/4: С3 (23/7, -1/7).
Уравнение биссектрисы lC = CC3 получается как уравнение прямой,
проходящей через точки С3 и С (5, 5):
y 5
x 5
1 7 5 23 7 5
или
3х – у – 10 = 0.
Ответ: д)у = 2, х+у–6=0, 3х–у–10=0
Решение задачи 1
41.
Прямая на плоскости.Оглавление:
2-ой способ. Уравнение биссектрисы lC = CC3 может быть найдено
из условия того, что точки биссектрисы CC3 равноудалены от сторон
АС и СВ.
Вычислим отклонения точки (х,у), лежащей на биссектрисе, от
сторон АС и СВ :
x 2y 5
2 x y 15
АС
,
СB
.
5
5
Оба отклонения отрицательны, так как начало координат и точки
биссектрисы треугольника лежат по одну сторону от каждой из сторон
АС и СВ.
dАС = dСВ AC CB :
x 2y 5
2 x y 15
l : 3х – у – 10 = 0.
C
5
5
Решение задачи 1
Ответ: д)у = 2, х+у–6=0, 3х–у–10=0
42.
Прямая на плоскости.lА :
АС
Оглавление:
x 2y 5
0 , так как начало координат и биссектриса l лежат
А
5
по одну сторону от стороны АС;
AB
x 2y 3
0 , так как начало координат и биссектриса l лежат
А
5
по разные стороны от стороны АВ.
x 2y 5 x 2y 3
- АС = АВ,
,
5
5
4у = 8,
lА: у = 2.
х – 2у + 5 = х + 2у –3,
lВ: х+у – 6 = 0.
Решение задачи 1
Ответ: д)у = 2, х+у–6=0, 3х–у–10=0
43.
Прямая на плоскости.Оглавление:
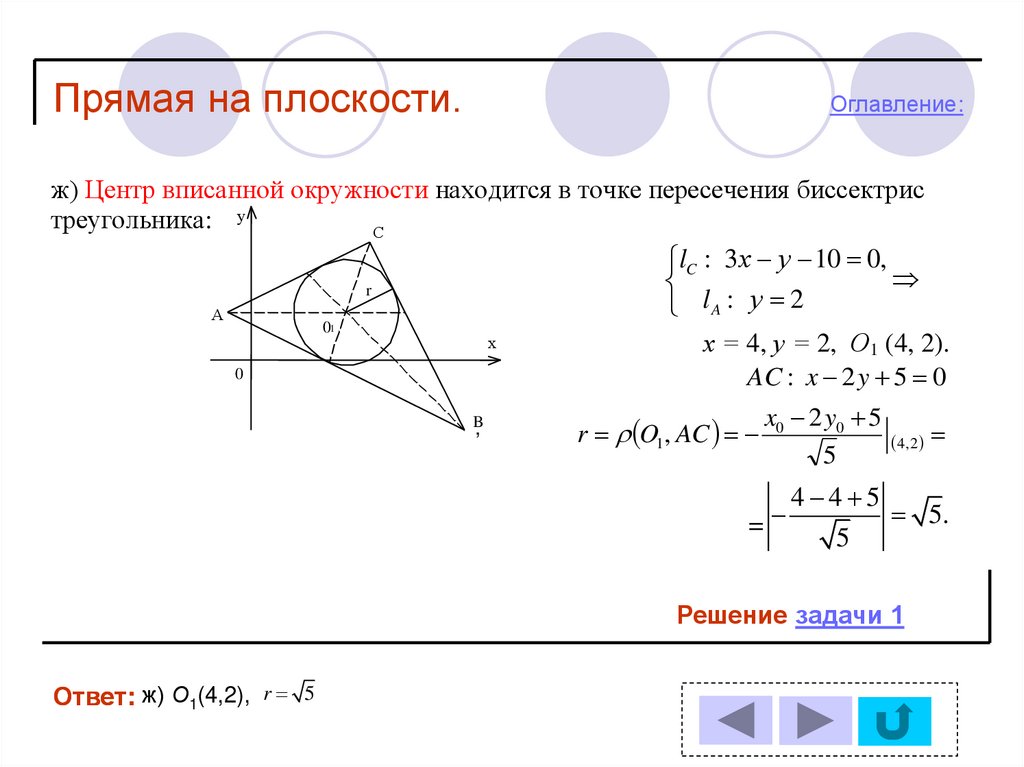
ж) Центр вписанной окружности находится в точке пересечения биссектрис
треугольника: у
С
lC : 3 х у 10 0,
r
lA : у 2
А
0
х
х = 4, у = 2, О1 (4, 2).
0
AC : x 2 y 5 0
1
B
,
r O1, AC
x0 2 y0 5
5
=
4, 2
4 4 5
5.
5
Решение задачи 1
Ответ: ж) О1(4,2),
r 5
44.
Прямая на плоскости.Оглавление:
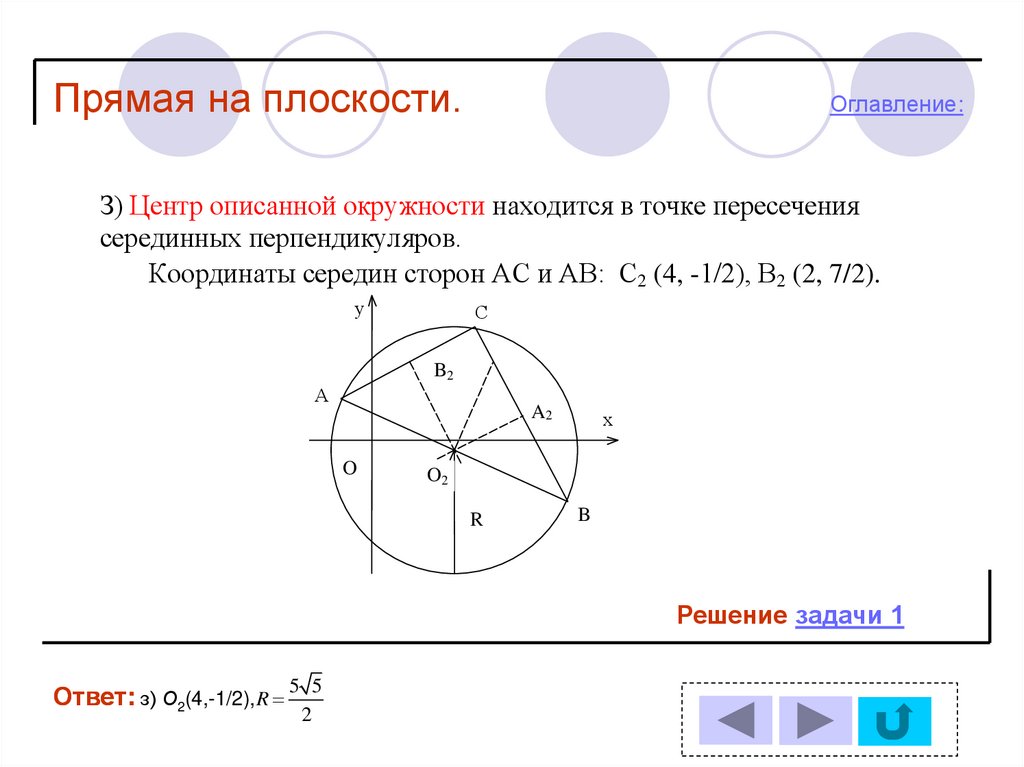
З) Центр описанной окружности находится в точке пересечения
серединных перпендикуляров.
Координаты середин сторон АС и АВ: С2 (4, -1/2), В2 (2, 7/2).
у
С
BB
22
А
,
O0
A2
х
O2
R
R
B
Решение задачи 1
Ответ: з) О2(4,-1/2), R
5 5
2
45.
Прямая на плоскости.Оглавление:
Угловые коэффициенты hC и hB равны 2 и -2 соответственно, и эти
прямые проходят через точки С2 и В2 . Система уравнений, составленная из
уравнений серединных перпендикуляров:
2
1
h
:
y
2( x 4), 4 x 2 y 17 0,
C2
2
7
h : y 2( x 4), 4 x 2 y 15 0
B
2
2
2
х = 4, у = -1/2,
,
центр описанной окружности находится
в точке О2 (4, -1/2).
Центр описанной окружности прямоугольного треугольника - середина
гипотенузы АВ: R
1
5 5
AB
.
2
2
Решение задачи 1
Ответ: з) О2(4,-1/2), R
5 5
2
46.
Прямая на плоскости.Оглавление:
и) Центр тяжести треугольника находится в точке пересечения
медиан:
mC : 11x 2 y 45 0,
mB : 13 x 14 y 75 0
х = 4,33, у = 1,3,
О3 (4,33; 1,3).
Решение задачи 1
Ответ:
и)
xO3 4,33;
yO3 1,33,
47.
Прямая на плоскости.Оглавление:
Другой способ. Медианы треугольника делятся точкой
пересечения в отношении 2 : 1, считая от вершины:
СО3 2
С3С2 1
xC 2 xC2 5 2 4
4,33;
xO3
3
3
yC 2 yC2 5 2 ( 1 2)
1,33.
yO3
3
3
Решение задачи 1
Ответ:
и)
xO3 4,33;
yO3 1,33,
48.
Прямая на плоскости.Оглавление:
к) Внутренние углы треугольника могут
быть найдены через угловые
коэффициенты прилежащих сторон:
tg A
k AC k AB
1 2 ( 1 2)
4
1 k AC k AB 1 1 2 ( 1 2) 3
A arctg
4
3
Решение задачи 1
Ответ:
A arctg
4
3
49.
Прямая на плоскости.Оглавление:
л) Площадь треугольника:
1
1
9
S
1)
2
5
2)
2
1
3 1
5
1
1
60 30 (кв. ед.).
2
S = p r,
p – полупериметр треугольника; r – радиус вписанной окружности,
p
3 5 5 5 4 5
6 5, r 5 S 30 (кв. ед.).
5
Решение задачи 1
Ответ:
л) 30
50.
Прямая на плоскости.Оглавление:
А (3, 1) и В (5, 2) АВ,
х 3 у 1
1
1
АВ :
у х .
2
1
2
2
Уравнение перпендикуляра РМ из точки Р(4, 9) на прямую АВ:
1
k
1 k 2.
у – 9 = k (x – 4);
2
1
1
x 7,
АВ : y x ,
2
2
y
3
РМ : y 2 x 17,
М x, y : 7,3 - проекция Р на АВ.
Решение задачи 2
Ответ: 7,3
51.
Прямая на плоскости.Оглавление:
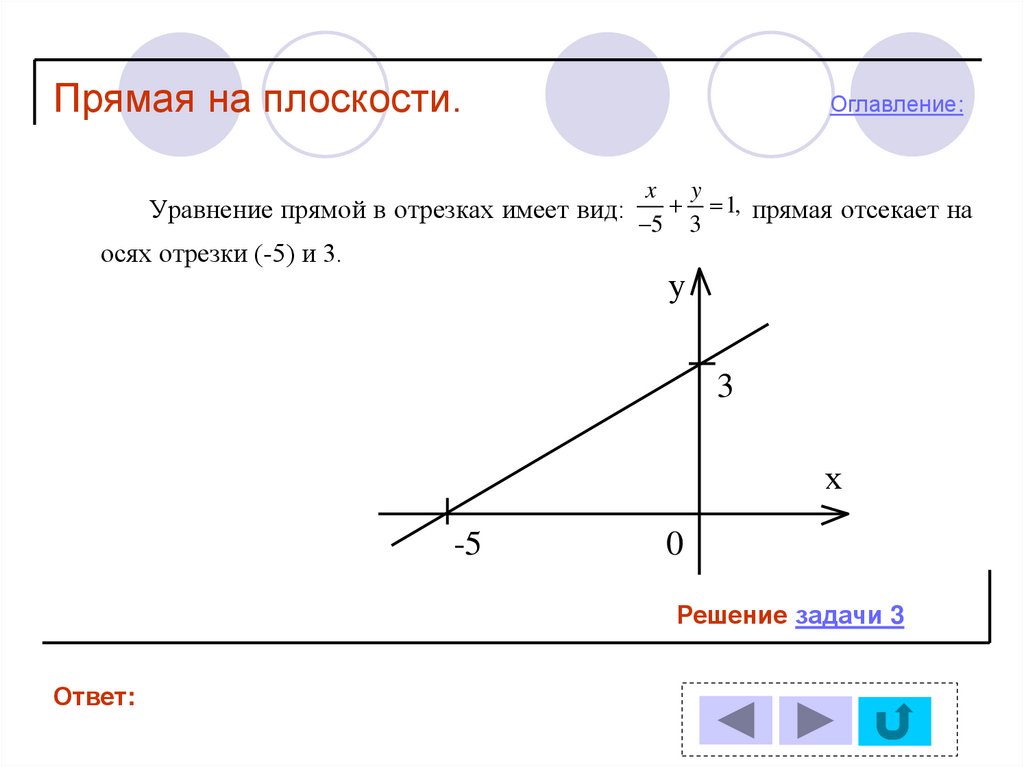
x y
1, прямая отсекает на
Уравнение прямой в отрезках имеет вид:
5 3
осях отрезки (-5) и 3.
у
3
х
-5
0
Решение задачи 3
Ответ:
52.
Прямая на плоскости.Оглавление:
2
,
7
3
L2 : 7х +15у +1 = 0, k2
15
Прямые L1 : 2х + 3у – 5 = 0, k1
пересекаются, так как они имеют разные угловые
коэффициенты. Составим уравнение пучка прямых, проходящих
через точку их пересечения М:
2х + 3у – 5 + (7х + 15у +1) = 0,
(2 + 7 ) х + (3 + 15 ) у + (-5 + ) = 0
Выделим в этом пучке искомую прямую
L : y kx b
Ответ:
5х + 12у + 6 = 0.
Решение задачи 4
53.
Прямая на плоскости.Оглавление:
По условию искомая прямая перпендикулярна
прямой
12
k
12х – 5у – 1 = 0, для которой 3
L3 :
5
k
1
k3
,
2 7
5
3 15
12
= -1 и уравнение искомой прямой:
5х + 12у + 6 = 0.
Решение задачи 4
Ответ:
5х + 12у + 6 = 0.
54.
Прямая на плоскости.Оглавление:
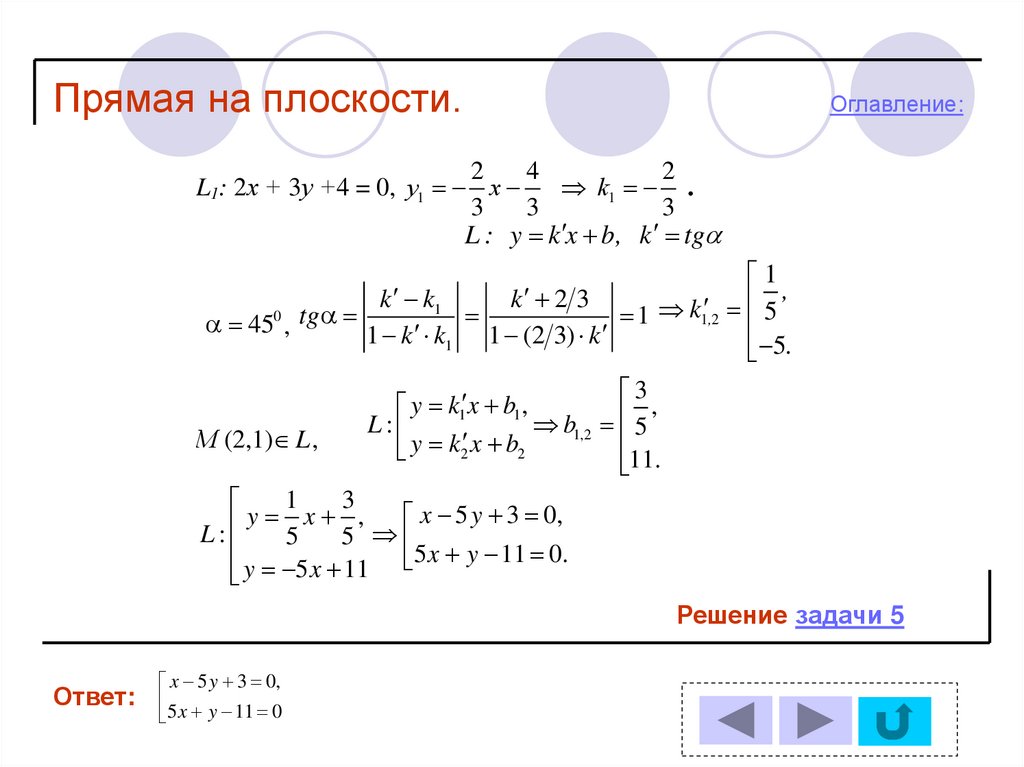
2
4
2
L1: 2х + 3у +4 = 0, у1 x
k1 .
3
3
3
L : y k x b, k tg
1
,
k 2 3
k k1
k
5
1,2
450 , tg 1 k k 1 (2 3) k 1
1
5 .
3
,
y k1 x b1 ,
b1,2 5
L:
М (2,1) L ,
b
x
k
y
2
2
11.
3
1
,
x
y
x 5 y 3 0,
L:
5
5
5 x y 11 0.
11
x
5
y
Решение задачи 5
Ответ:
x 5 y 3 0,
5 x y 11 0
55.
Прямая на плоскости.Оглавление:
1-ый способ.
L1
L
L2
Уравнение прямой L будем искать в виде
y
А(х – х0) + В(у + у0) = 0.
В качестве нормального вектора n { A, B}
можно выбрать нормальный вектор прямых
x
L1: х + 2у – 1 = 0 и L1: х + 2у – 1 = 0, равный {1, 2}.
0
Найдем какую-нибудь точкуМ0 (х0, у0) L.
Точка М0 будет делить пополам отрезок,
M (x,y)
соединяющий две любые точки,
лежащие на L1 и L2.
Например, (подбором!) М1 (1, 0) L1 и М2 (-2, 0) L2, тогда точка М0
имеет координаты середины М1М2 (-1/2, 0), и уравнение прямой L
принимает вид: х + 2у + 1/2 = 0.
Решение задачи 6
Ответ: х+2у+1/2=0
56.
Прямая на плоскости.Оглавление:
2 –ой способ.
Произвольная точка М (х, у) L, если
(М, L1) = (М, L2) .
Для снятия модуля определим знаки отклонений точки М (х, у) от
прямых L1 и L2. Для этого нужно выяснить взаимное расположение
начала координат, точки М (х, у) и прямых L1 и L2.
Приведем уравнения прямых к нормальному виду:
L1 :
1
2
1
1 2
x
y
0, n1 ,
,
5
5
5
5 5
L2 :
1
2
1
1 2
x
y
0, n2 ,
,
5
5
5
5 5
где n1 и n2 - единичные векторы нормалей к прямым L1 и L2,
проведенным из начала координат.
Решение задачи 6
Ответ: х+2у+1/2=0
57.
Прямая на плоскости.Оглавление:
Видим, что n1 и n2 противоположны по направлению, значит, начало
координат лежит в полосе между прямыми L1 и L2. Точка М и начало
координат лежат по одну сторону как от прямой L1, так и от прямой L2,
значит, отклонения точки М от прямых L1 и L2 имеют один и тот же
отрицательный знак.
Из
x 2 y 1 x 2 y 2
следует, что
5
5
х + 2у – 1 = -х – 2у – 2 и х + 2у + 1/2 = 0.
Решение задачи 6
Ответ: х+2у+1/2=0











































 mathematics
mathematics








