Similar presentations:
Кинематика твердого тела. Плоское движение. Определение ускорений точек
1.
КИНЕМАТИКАТема 3. Кинематика твердого тела
Плоское движение.
Определение ускорений точек.
2.
Определение ускорений точек плоской фигурыВывод. Ускорение любой точки М
плоской
фигуры
геометрически
складывается из ускорения какой нибудь другой точки А, принятой за
полюс, и ускорения, которое точка М
получает при вращении фигуры
вокруг этого полюса, то есть
аM
а
A
а
MA
.
аМ
аA
аМА
аA
А
М
(1)
Этот вывод основывается на положении о том, что плоское
движение раскладывается на поступательное движение
вместе с полюсом и вращательное движение вокруг полюса.
3.
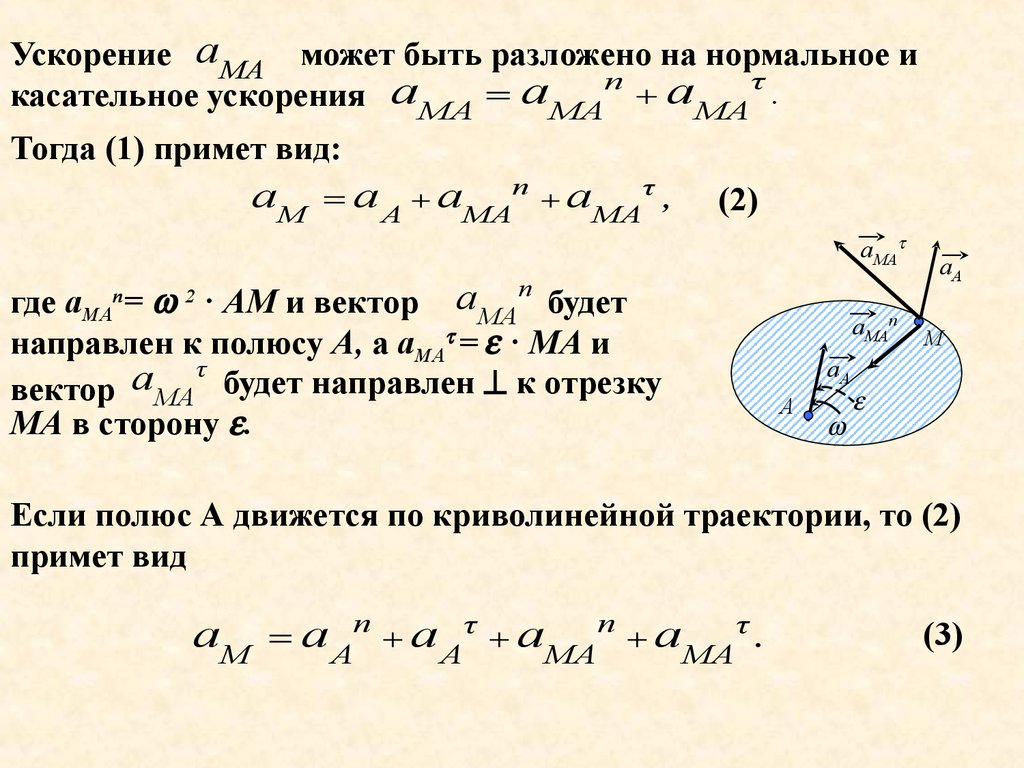
Ускорение а MA можетбыть разложено
и
n на
нормальное
касательное ускорения а MА а МA а MA τ .
Тогда (1) примет вид:
аM
n τ
а а
а
,
A
MA
МА
(2)
n
n
2
где аМА = · АМ и вектор аМA будет
направлен
к
полюсу
А,
а
а
= · МА и
МА
τ
вектор аМA будет направлен к отрезку
МА в сторону .
аМА
аМАn
аA
А
аA
М
Если полюс А движется по криволинейной траектории, то (2)
примет вид
аM
n τ n τ
а
а
а
а
.
A
А
MA
МА
(3)
4.
n τ n τМодули и направления ускорений: а A , а А , а MA , а МА
обычно удается определить, поэтому для нахождения
полного ускорения можно применять метод проекций.
Проектируя векторное равенство (3) на оси координат,
получим:
аМх = аАхn + аАх + аМАхn + аМАх ,
аМу= аАуn + аАх + аМАуn + аМАу ,
(4)
аМz = аАzn + аАz + аМАzn + аМАz .
Вычисляя правые части в выражениях (4) найдем проекции
вектора полного ускорения на оси координат, тогда его
модуль и направление определиться по формулам:
аМ
а
2
Мх
а 2Му а 2Мz
соs а Мx / | а М |, сos а Му / | а М |, cos а Мz / | а М | .
5.
Пример определения ускорений точек плоской фигурыЦентр С, движущегося в
вертикальной плоскости диска, имеет
уравнения движения хС = 2t (м) и
уС = - t 2 +1 (м). Закон вращения диска
вокруг оси, перпендикулярной к его
плоскости, = t 2/4 (рад). Радиус
диска R = 1 м.
у
1
= (t)
М
хС
C
уС
1
О
450
2
C
М
х
Определить ускорение точки М диска в момент времени t1=1 c.
Решение
1. Определим положение диска и точки М в момент времени t1.
Координаты точки С: хС1 = 2 · 1= 2; уС 1= - 12 +1 = 0. Положение
точки М определяется углом 1 = · 12/4 = /4 = 450.
6.
2. Выберем полюс и применим метод проекций.Для определения ускорения точки М воспользуемся
формулой (2), принимая
вn качестве
τ полюса точку С. Тогда
получим а M аС а MС а МС .
Или в проекциях на оси координат
аМх = аСх + аМСхn + аМСх ,
аМу= аСу + аМСуn + аМСу .
(1)
3. Определим величины, входящие в правые части равенств (1).
аСх х С 0; аСу у С 2.
Величину аМСn найдем по формуле аМСn = 2 · СМ =
2
· СМ
= t 2/4|t=1= /4.
(2)
7.
аn
Вектор МС будет направлен к
центру диска, то есть к точке С.
а
у
Проекции на оси вектора
МС
аМСхn =- аМСn · cos 450 = - 2 /8 = - 0,56,
аМСуn = - аМСn · cos 450 = - 0,56.
(3)
а
М
n
450
1
О
2
C
а
n
МС
МС
х
Величину аМС найдем по формуле аМС = ·СМ = · СМ = /2.
Вектор а
τ
будет направлен по касательной, т. е. отрезку СМ.
τ
Проекции на оси вектора а МС
аМСх = аМС · cos 450 = · 2 / 4 = 1,11,
(4)
0
аМСу = - аМС · cos 45 = - 1,11.
МС
Подставляя значения (2) – (4) в выражения (1), получим
аМх = 0 – 0,56 + 1,11 = 0,55,
аМу= - 2 - 0,56 - 1,11 = - 3,67.
τ
8.
Модуль и направление вектора ускорения точки М определимпо формулам:
| a M | а Мx 2 а2Му 0 ,55 2 ( 3,67 )2 3,71 м / с 2 .
cos ( ) = аМх / |аМ| = 0,55 / 3,71 = 0,15.
= аrccos (0,15) = 1,42 рад. 810.
Изобразим вектор ускорения на рисунке
у
М
а
Мх
810
450
1
О
2
C
а
Му
а
М
х







 physics
physics








