Численное решение гиперболических систем уравнений

1.

Математические вопросы численного решения гиперболических систем уравнений
1. Определение гиперболической квазилинейной системы уравнений 1
порядка.
2.Характеристическая форма гиперболической системы уравнений.
Инварианты Римана
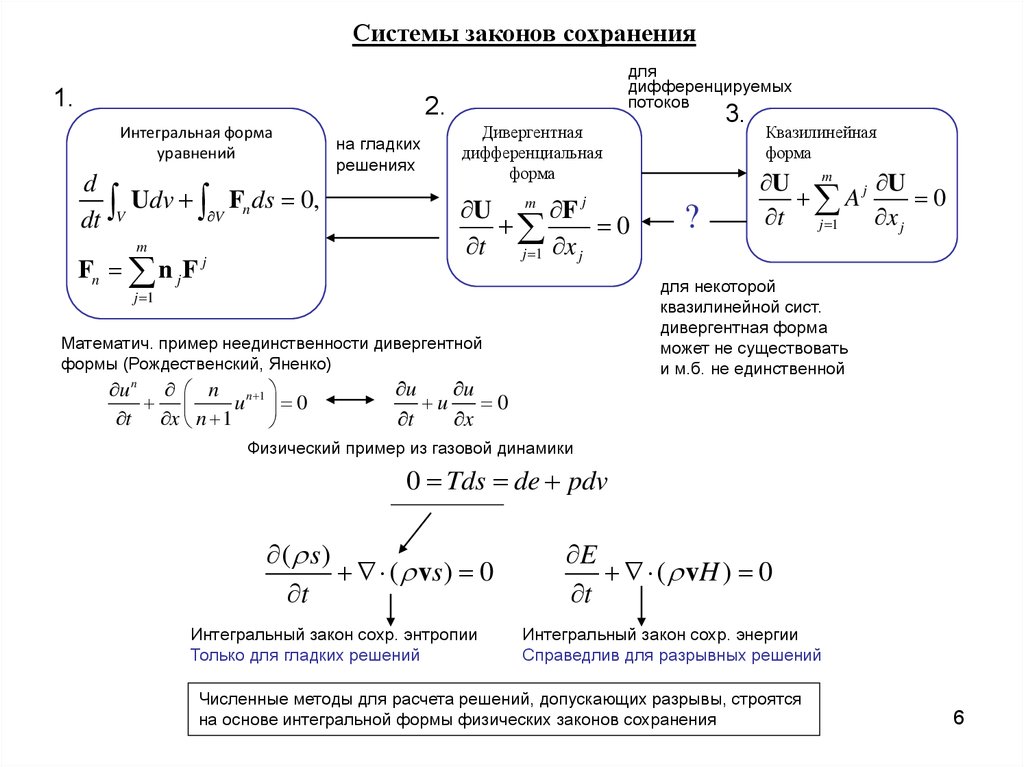
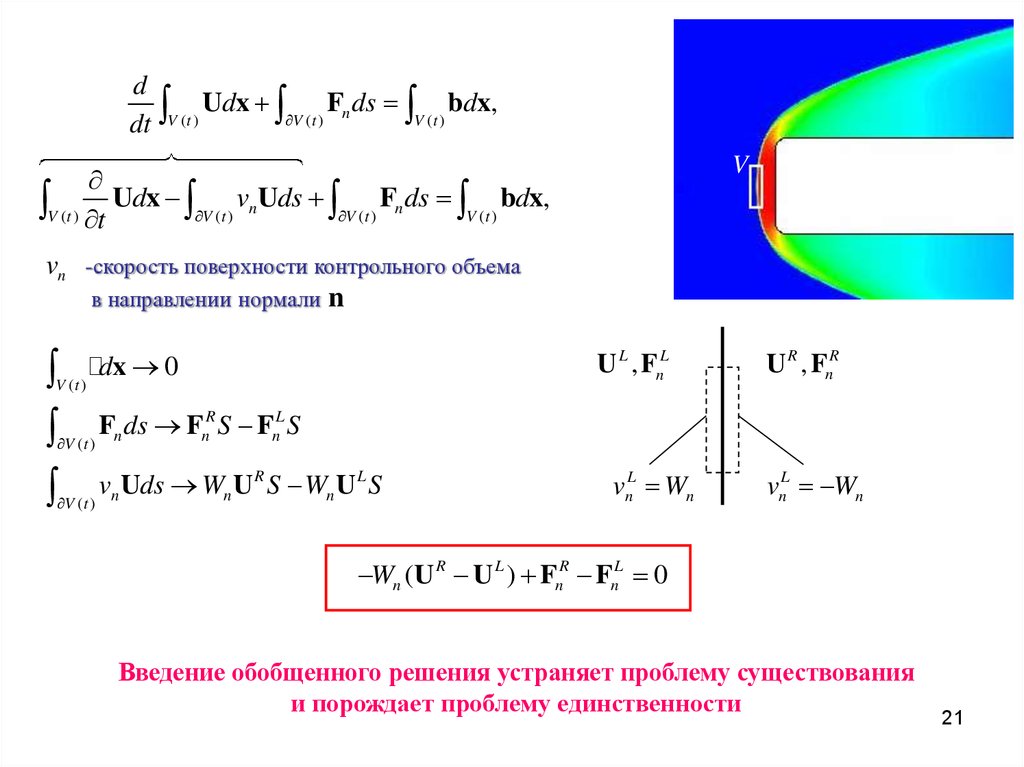
3. Системы законов сохранения в интегральной и дифференциальной форме
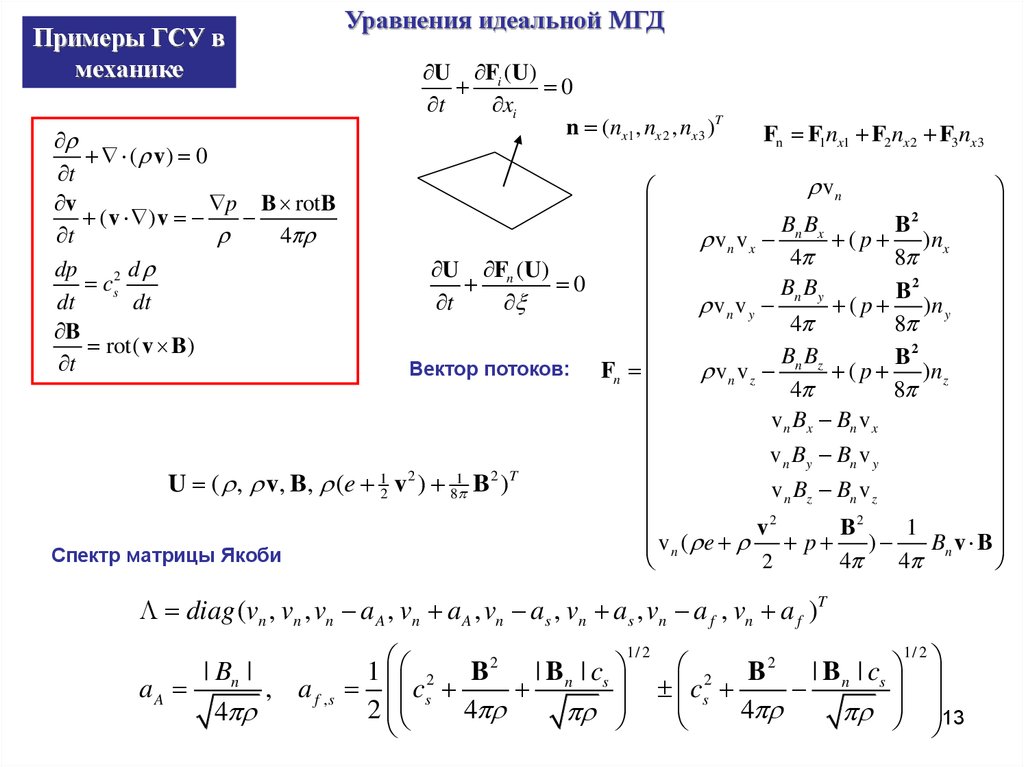
4. Примеры гиперболических систем уравнений в механике
5. Симметризация законов сохранения. Энтропия.
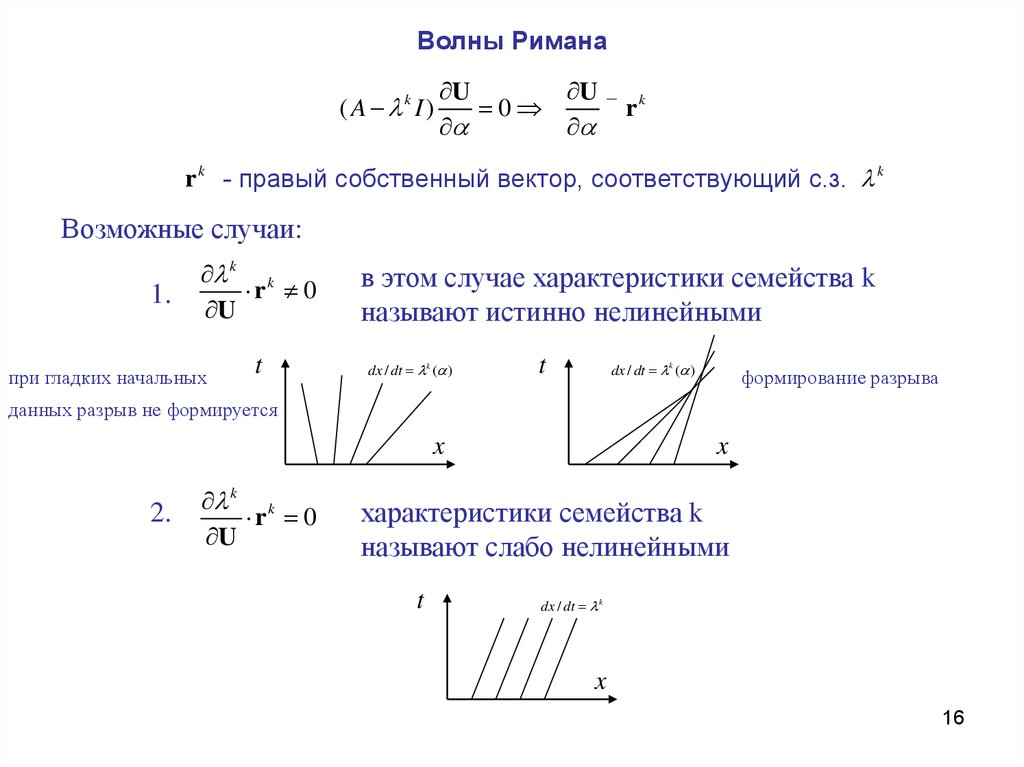
6. Волны Римана
7. Истинно нелинейные и слабо нелинейные семейства характеристик
1

2.

Определение гиперболической квазилинейной системы
уравнений 1 порядка.
(Общий вид квазилинейной системы уравнений первого порядка)
Пусть матрица A не особая
(далее штрих опускаем)
Введем матрицу P(n):
2

3.

Система уравнений
описывает одномерный процесс в направлении, заданном вектором
После умножения на левый собственный вектор lk
U
U k
lk
k
l f
xn
t
Система уравнений в
характеристической форме
3

4.

Инварианты Римана
Соотношения на характеристиках устанавливают связь между дифференциалами
различных переменных в направлении характеристик dx/dt=λk
Интегрирование дифференциальных соотношений на характеристиках в тех случаях,
когда оно возможно, приводит к записи системы уравнений в инвариантах Римана
Пусть lk зависит только от x, t
U k
U
l
k
l f
t
x
k
k
k
l k
(l k U)
k (l U)
k
k l
l f
U
t
x
t
x
k
wk
k w
f ',
t
x
wk l k U
Замечание 1. В случае линейной системы уравнений при f=0, инварианты
Римана сохраняют свое значение на характеристиках системы уравнений
Замечание 2. В случае n=2 гиперболическая система всегда может быть расширена,
до системы, записанной в инвариантах Римана.
(Подстановка p=