Численные методы решения нелинейных уравнений и систем нелинейных уравнений

1. Математическое моделирование систем и процессов

ЧИСЛЕННЫЕ МЕТОДЫ
решения нелинейных уравнений и
систем нелинейных уравнений
1

2.

ЭТАПЫ ПРИБЛИЖЕННОГО ПОИСКА КОРНЕЙ
НЕЛИНЕЙНОГО УРАВНЕНИЯ
1. отделение корня
2. уточнение корня
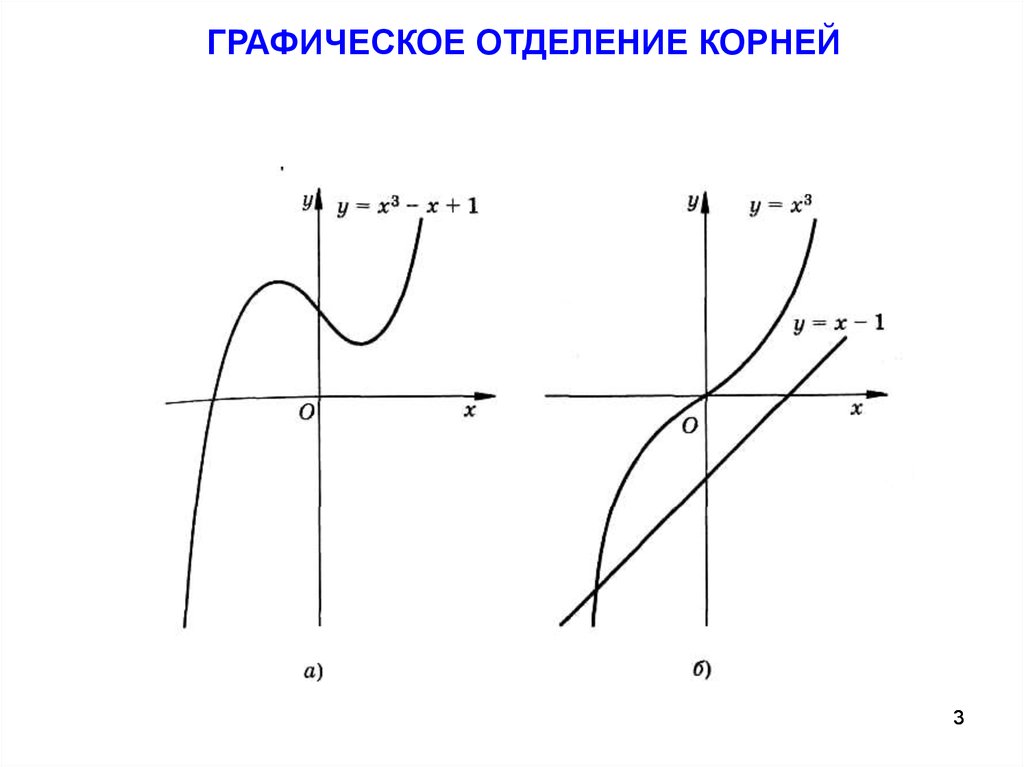
Отделение корня - это определение промежутка, содержащего один и
только один корень уравнения.
Одна из точек этого промежутка принимается за начальное
приближение корня.
ТЕОРЕМА. Если функция f(x), определяющая уравнение f(x) = 0 , на
концах отрезка a, b принимает значения разных знаков, т. е.
f (a) f (b) 0
(1)
то на этом отрезке содержится по крайней мере один корень уравнения.
Если же функция f(x) непрерывна и дифференцируема и ее
производная сохраняет знак внутри отрезка a, b , то на этом отрезке
*
находится только один корень x уравнения.
2

3.

ГРАФИЧЕСКОЕ ОТДЕЛЕНИЕ КОРНЕЙ
3

4.

ШАГОВОСТЬ И ПОРЯДОК СКОРОСТИ СХОДИМОСТИ
Скорость сходимости процесса
Метод имеет n-й порядок сходимости, если
x
( k 1)
или
( k 1)
x Cx
*
(k )
x
* n
C
(k ) n
С - постоянная, не зависящая от n.
Шаговость процесса
Метод является n-шаговым, если для построения итерационной
последовательности нужно вычислить функцию в n точках.
4

5.

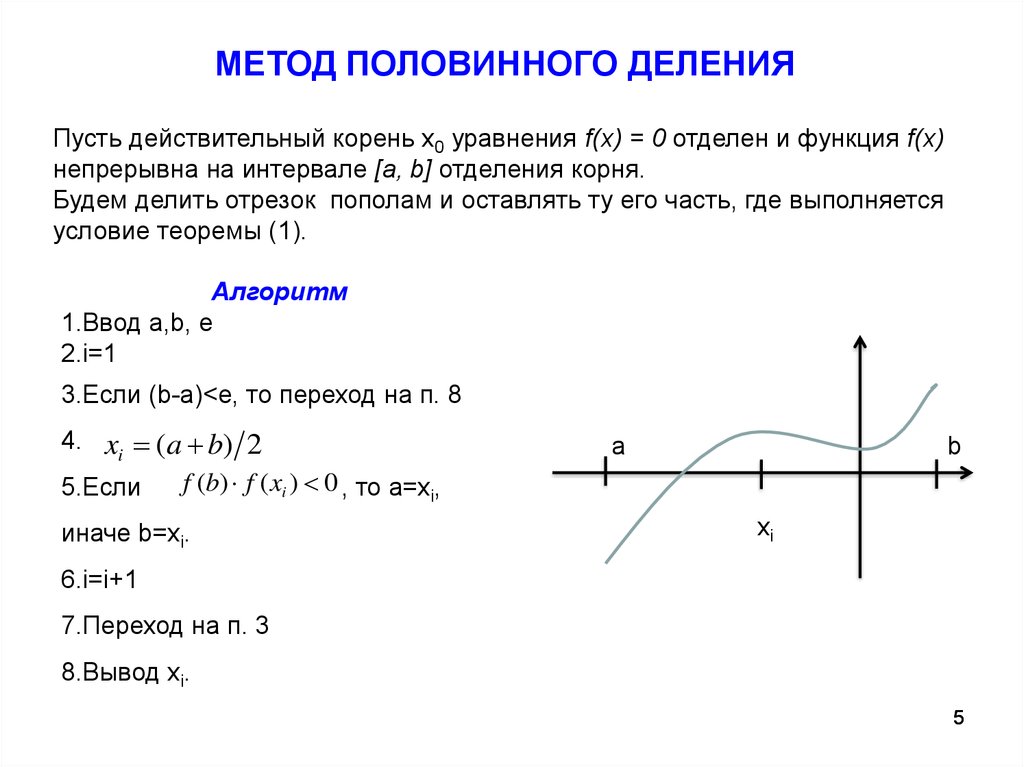
МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ
Пусть действительный корень х0 уравнения f(x) = 0 отделен и функция f(x)
непрерывна на интервале [a, b] отделения корня.
Будем делить отрезок пополам и оставлять ту его часть, где выполняется
условие теоремы (1).
Алгоритм
1.Ввод а,b, e
2.i=1
3.Если (b-a)<e, то переход на п. 8
4. xi (a b) 2
f (b) f ( xi ) 0 , то a=xi,
5.Если
иначе b=xi.
a
b
xi
6.i=i+1
7.Переход на п. 3
8.Вывод xi.
5

6.

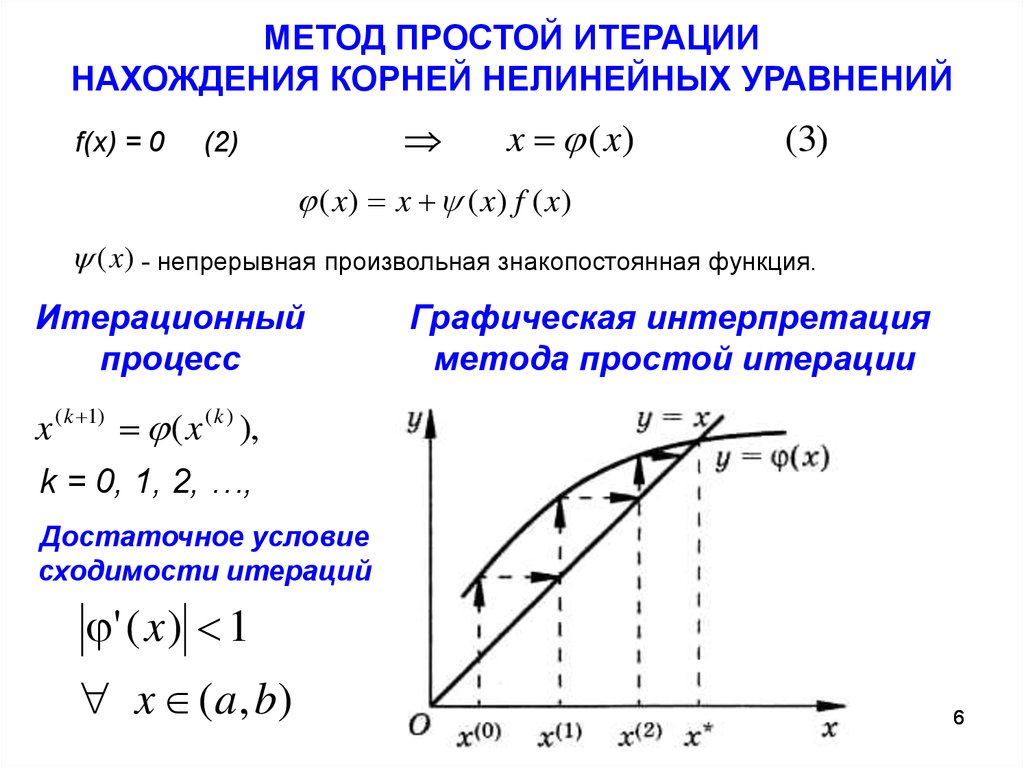
МЕТОД ПРОСТОЙ ИТЕРАЦИИ
НАХОЖДЕНИЯ КОРНЕЙ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
f(x) = 0
(2)
x (x)
(3)
( x) x ( x) f ( x)
(x) - непрерывная произвольная знакопостоянная функция.
Итерационный
процесс
Графическая интерпретация
метода простой итерации
x ( k 1) ( x ( k ) ),
k = 0, 1, 2, …,
Достаточное условие
сходимости итераций
' ( x ) 1
x ( a , b)
6

7.

ТИПОВЫЕ СЛУЧАИ УСТОЙЧИВОЙ И НЕУСТОЙЧИВОЙ
РЕАЛИЗАЦИИ МЕТОДА ПРОСТОЙ ИТЕРАЦИИ
7

8.

КЛАССИЧЕСКИЙ ПРИМЕР
ВЫЧИСЛЕНИЯ КВАДРАТНОГО КОРНЯ
f ( x) x a 0(a 0)
2
(x )
a
x
' ( x)
a
2
x
Поведение
Сходимость
метода
' ( x) 1
Не сходится
' ( x)
при
x a
' ( x) <1
x2 x a
( x a / x)
2
2x 1
(x a / x2 )
2
при
x ( 1,0),
' ( x) 0
Сходится
в
ограниченном
интервале
к
отрицательному
значению корня
Сходится,
и
очень быстро
при x a
8

9.

МЕТОД НЬЮТОНА
приближенное значение корня
x
( k 1)
x
(k )
(k )
f (x )
.
(k )
f '(x )
(4)
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
МЕТОДА НЬЮТОНА
метод Ньютона
•имеет вблизи корня второй
порядок сходимости.
•является одношаговым.
9

10.

ПРЕИМУЩЕСТВА И НЕДОСТАТКИ
МЕТОДА НЬЮТОНА
Преимущества:
1) квадратичная сходимость,
2) возможность обобщения на случай систем уравнений,
3) метод является одношаговым.
Недостатки:
1) Расходится в тех областях,
где
f ' ( x) 0
2) если функция f(x) задана таблично,
то вычисление f ' ( x) затруднено
Пути устранения:
Модифицированный
метод Ньютона
Метод секущих
10

11.

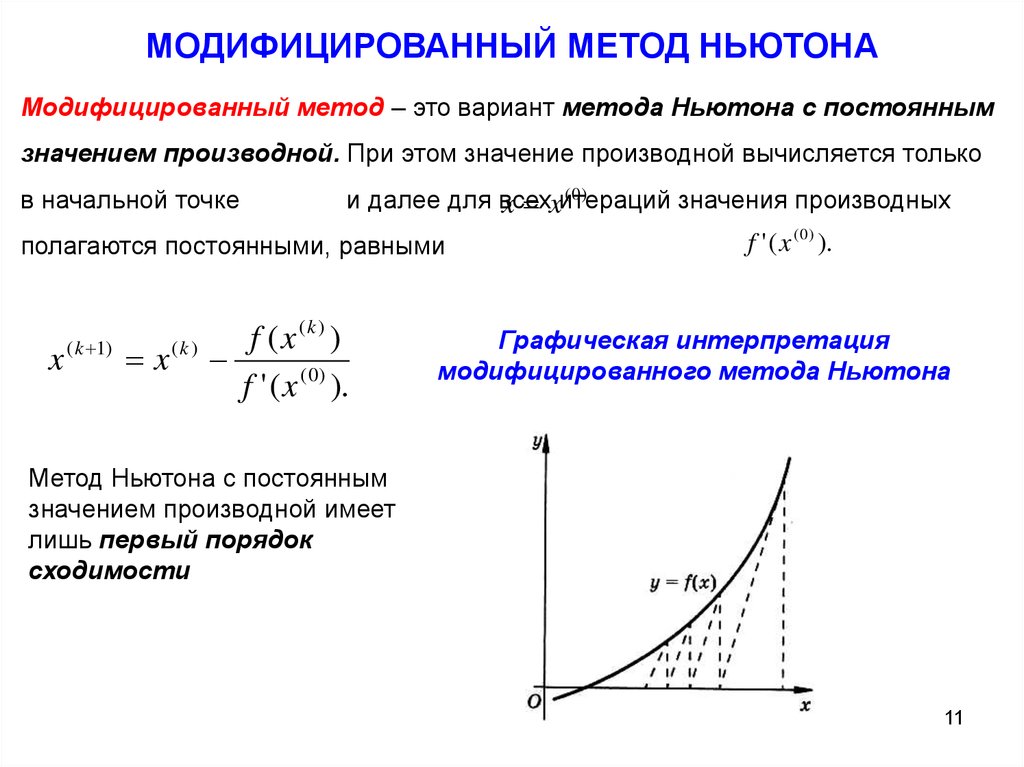
МОДИФИЦИРОВАННЫЙ МЕТОД НЬЮТОНА
Модифицированный метод – это вариант метода Ньютона с постоянным
значением производной. При этом значение производной вычисляется только
в начальной точке
(0)
и далее для всех
значения производных
x xитераций
полагаются постоянными, равными
x ( k 1) x ( k )
f ( x (k ) )
f ' ( x ( 0) ).
f ' ( x ( 0) ).
Графическая интерпретация
модифицированного метода Ньютона
Метод Ньютона с постоянным
значением производной имеет
лишь первый порядок
сходимости
11

12.

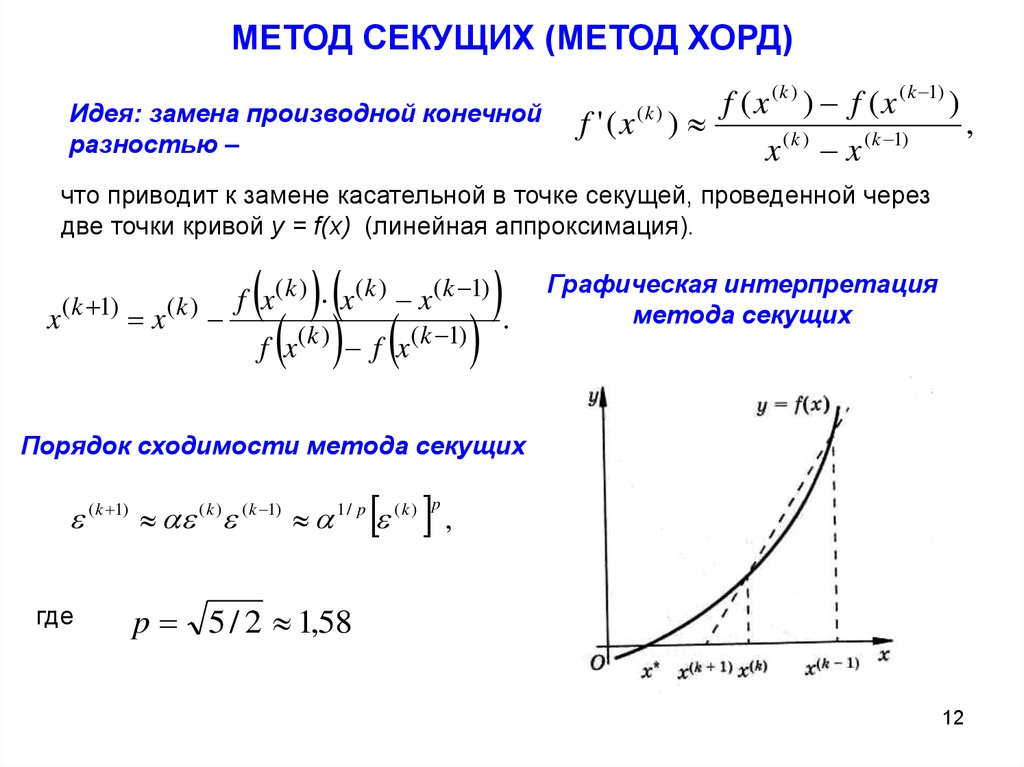
МЕТОД СЕКУЩИХ (МЕТОД ХОРД)
Идея: замена производной конечной
разностью –
(k )
( k 1)
f
(
x
)
f
(
x
)
f ' ( x (k ) )
,
(k )
( k 1)
x x
что приводит к замене касательной в точке секущей, проведенной через
две точки кривой y = f(x) (линейная аппроксимация).
x ( k 1) x ( k )
.
f x( k ) f x ( k 1)
f x ( k ) x( k ) x ( k 1)
Графическая интерпретация
метода секущих
Порядок сходимости метода секущих
( k 1) ( k ) ( k 1) 1 / p ( k ) ,
p
где
p 5 / 2 1,58
12

13.

МЕТОД ПРОСТОЙ ИТЕРАЦИИ НАХОЖДЕНИЯ КОРНЕЙ
СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
f(x) = 0
x ( x1 , x 2 ,..., x n ) T
(1)
- вектор-столбец неизвестных,
f ( x) f1 ( x), f 2 ( x),..., f n ( x)
T
- вектор-столбец функций
x (x)
(2)
( x) 1 ( x), 2 ( x),..., n ( x) ,
T
или
x1 1 ( x1 , x 2 ,..., x n ),
x ( x , x ,..., x ),
2
2
1
2
n
.................................
x n n ( x1 , x 2 ,..., x n ).
(3)
13

14.

МЕТОД ПРОСТОЙ ИТЕРАЦИИ НАХОЖДЕНИЯ КОРНЕЙ
СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Итерационный процесс
Начальное приближение для корня
x
(0)
( x , x ,..., x
(0)
1
(0)
2
(0) T
n
) ,
Формула расчета значения на (k+1) итерации
x ( k 1) ( x ( k ) ), k 0,1,2,...,
или
x1( k 1) 1 x1( k ) , x 2( k ) ,..., x n( k ) ,
( k 1)
(k )
(k )
(k )
x 2 2 x1 , x 2 ,..., x n ,
...........................................
x ( k 1) x ( k ) , x ( k ) ,..., x ( k ) .
n 1
2
n
n
Вектор погрешности испытывает линейное преобразование,
(метод имеет первый порядок сходимости)
14

15.

СХОДИМОСТЬ МЕТОДА ПРОСТОЙ ИТЕРАЦИИ
РЕШЕНИЯ НЕЛИНЕЙНОГО УРАВНЕНИЯ
МАТРИЦА ЯКОБИ ФУНКЦИЙ
1 ( x)
x
1
A ....
n ( x)
x1
i (x)
1 ( x)
1 ( x)
...
x 2
x n
....
...
... ,
n ( x)
n ( x)
...
x 2
x n
x x*
Система принимает вид:
k 1
A .
k
Достаточное условие сходимости итераций
A 1
15

16.

МЕТОД ИТЕРАЦИЙ ЗЕЙДЕЛЯ
( k 1)
xi
( k 1)
( k 1)
(k )
i x1
,..., xi 1 , xi ,..., x n( k )
,
i 1,..., n.
МЕТОД НЬЮТОНА
Приближенное значение корня
x
( k 1)
x
(k )
A
( k ) 1
f
f (k ) ,
Условие сходимости
det( A(f k ) ) 0.
16

17.

МОДИФИЦИРОВАННЫЙ МЕТОД НЬЮТОНА
Модифицированный метод – это вариант метода Ньютона с постоянным
значением производной.
х
( k 1)
х
(k )
( 0) 1
f
А
f
(k )
Метод Ньютона с постоянным значением производной имеет первый
порядок сходимости:
17

18.

Вариант №21
Метод 2 – Метод простой итерации
ctg ( x)
x
0
2
Метод 3 – Метод Ньютона
sin( y 0,4) x 2 ;
2
x 2 y 2 8.
18