Моделирование информационных систем

1. Обнинский Институт Атомной Энергетики

2. Обнинский Институт Атомной Энергетики

МОДЕЛИРОВАНИЕ
ИНФОРМАЦИОННЫХ
СИСТЕМ
Гулина Ольга Михайловна
olga@iate.obninsk.ru
Сopyright © 2001 by Nataly Pashkova
E-mail: natik_pna@mail.ru

3. Вычисление интегралов методом Монте-Карло

Пусть - сл. в., М =m
b
M xp( x)dx, ,
a
1
ˆ
M
N
i 1
M 2 x 2 p( x)dx,
a
N
b
i
mˆ ,
mˆ N
m
P

4. Метод Монте-Карло

Mg g x p x dx
G
Z=g( ),

5. Общий метод оценки математических ожиданий

if D =b ,
2
1 N
xb
x
P i m
N
N i 1

6. Оценка эмпирической дисперсии

1 N 2
2
i M
N i 1
N
1
D i2 i
N
N i 1
i 1
N
1
2

7.

Общий метод оценки
математических ожиданий
I f ( P) p( P)dP,
G
p
(
P
)
dP
1
G
MZ I f ( P) p( P)dP,
G
1
ˆ
MZ
N
N
Z Q
i 1
i

8. Вычисление интегралов методом Монте-Карло

Пример:
I f x e dx,
kx
где k>0
0
-kx
Выберем p(x)=ke
-1
и f1=k f(x)
N
N
i 1
i 1
ˆI N 1 f kN 1 f
1 i
i

9. Алгоритм вычисления интеграла

1) формула для оценки интеграла;
2) формула для получения случайной
величины ;
3) формула для оценки погрешности

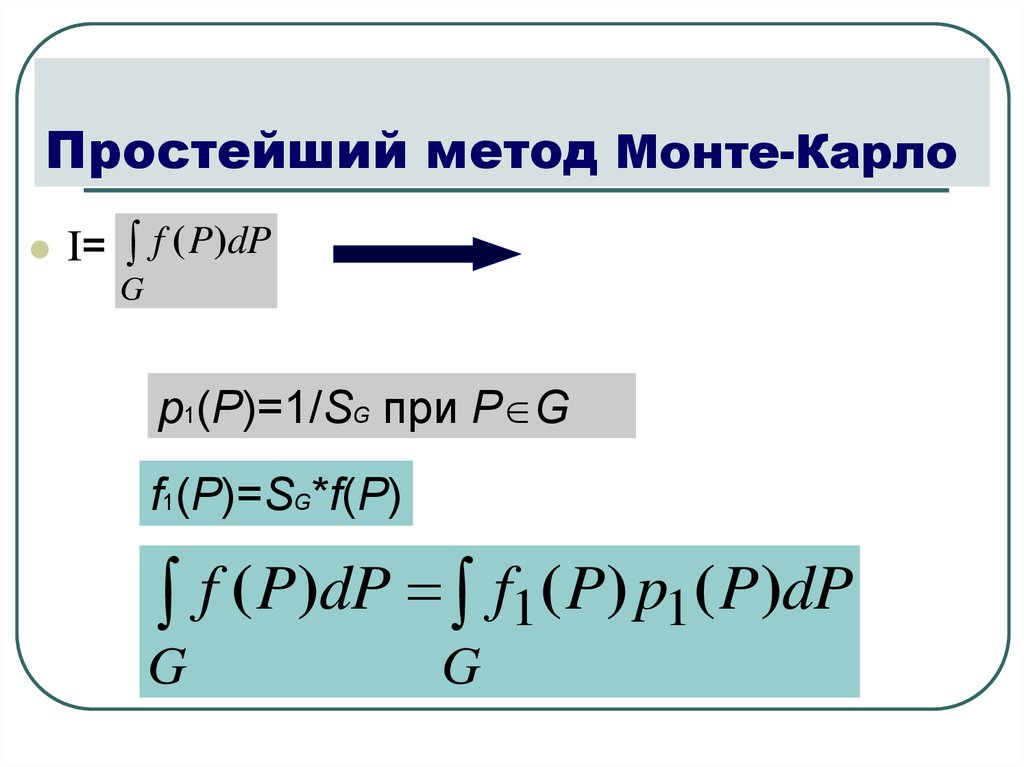
10. Простейший метод Монте-Карло

I= f ( P)dP
G
p1(P)=1/SG при P G
f1(P)=SG*f(P)
f ( P)dP f1 ( P) p1 ( P)dP
G
G

11.

Трудоемкость алгоритма
Монте-Карло
t*Dξ

12. Способы уменьшения дисперсии

1 Частичное аналитическое
интегрирование
1.1 Выделение главной части
1.2 Интегрирование по части области

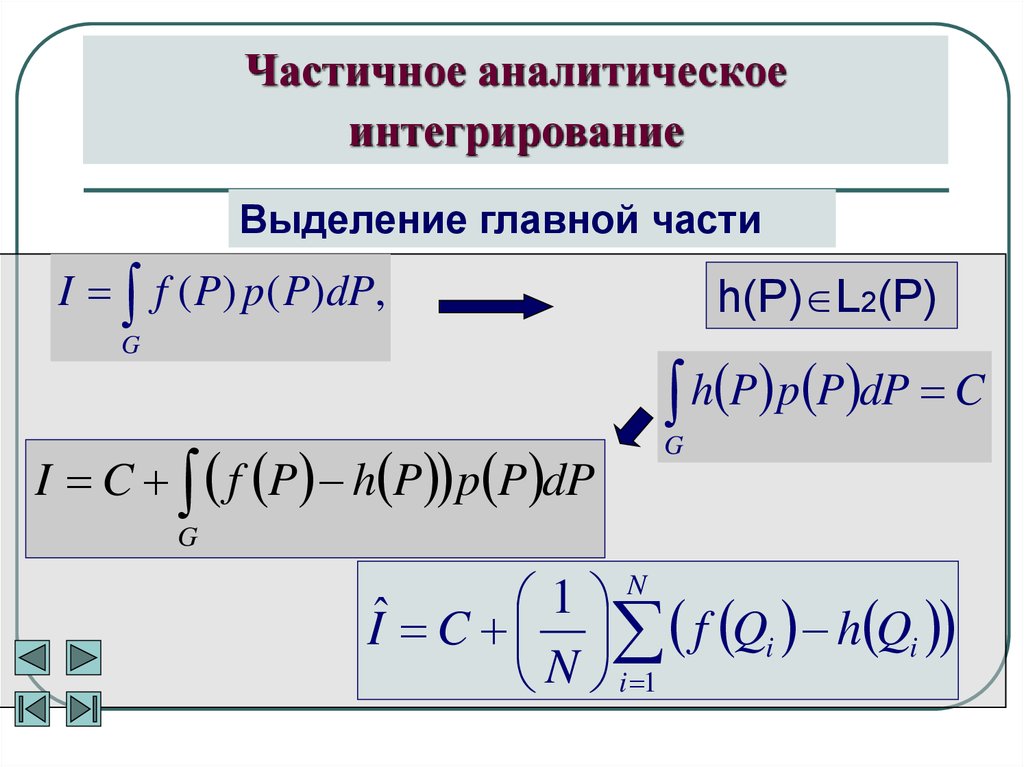
13. Частичное аналитическое интегрирование

Выделение главной части
I f ( P) p( P)dP,
G
I C f P h P p P dP
h(P) L2(P)
h P p P dP C
G
G
N
1
ˆI C f Q h Q
i
i
N i 1

14. Частичное аналитическое интегрирование

Выделение главной части
DZ f P h P p P dP I C
2
2
G
f
P
h
P
p
P
dP
,
2
если
G
то и DZ<

15. Частичное аналитическое интегрирование

Интегрирование по части области
I f ( P) p( P)dP,
G
I
f P p P dP C ,
f P p P dP C,
B
p P dP c,
B
где 0<c<1
G1
G1=G\B

16. Частичное аналитическое интегрирование

Интегрирование по части области
В
G1
p1(P)=p(P)/(1-c)
p( P)
I 1 c f P
dP C ,
1 c
G1
N
1
c
Iˆ C
f Qi
N i 1
DZ`<(1-c)DZ

17. 2 Метод существенной выборки

I 0 f P dP
G
f P dP 0
G
Плотность p(P), определенную в G,
назовем допустимой по отношению к
f(P), если p(P)>0 в тех точках, где
f(P) 0.

18. Метод существенной выборки

f P / p P , P G
Z 0 P
0, P G0 ,
MZ 0 Q Z 0 P p P dP f P dP I 0
G
G
1
Iˆ
N
N
Z Q
i 1
0
i

19. Метод существенной выборки

DZ 0 Z 02 P p P dP I 02 f 2 P / p P dP I 02
G
G
Теорема. Минимальная дисперсия DZ0
реализуется в случае, когда плотность
p(P) пропорциональна |f(P)|, и равна
2
2
ˆ
DZ 0 f P dP I 0
G

20. Метод существенной выборки

pˆ P
f P
f P dP
G
желательно выбирать плотность p(P)
по возможности пропорциональной |f(P)|
Метод предложен Г. Каном и называется
методом существенной выборки
(importance sampling)

21. Метод существенной выборки

Пример:
1
I e dx
x
ex 1+x+
0
p(x)=(2/3)(1+x) =>
ˆI 3
2N
N
i
1
3 x
1
I e 1 x p x dx
20
e
i 1 1 i
1 3 1