гар. осц

1. Литература

Динамика поступательного
движения
Введение
Литература
1
Тема: Гармонический осциллятор

2.

Динамика поступательного движения
Содержание
Введение. Виды колебаний
1. Математический маятник
2. Пружинный маятник
3. Скорость, ускорение, энергия
колеблющейся точки
4. Физический маятник
5. Колебательный контур
6. Гармонический осциллятор
Тема: Гармонический15.02.26
осциллятор
2

3. Понятие динамической системы

Динамика поступательного
движения
Введение
Понятие динамической системы
3
Тема: Гармонический осциллятор

4. Понятие динамической системы

Динамика поступательного
движения
Введение
Понятие динамической системы
4
Тема: Гармонический осциллятор

5. Понятие динамической системы

Динамика поступательного
движения
Введение
Понятие динамической системы
5
Тема: Гармонический осциллятор

6. Понятие динамической системы

Динамика поступательного
движения
Введение
Понятие динамической системы
6
Тема: Гармонический осциллятор

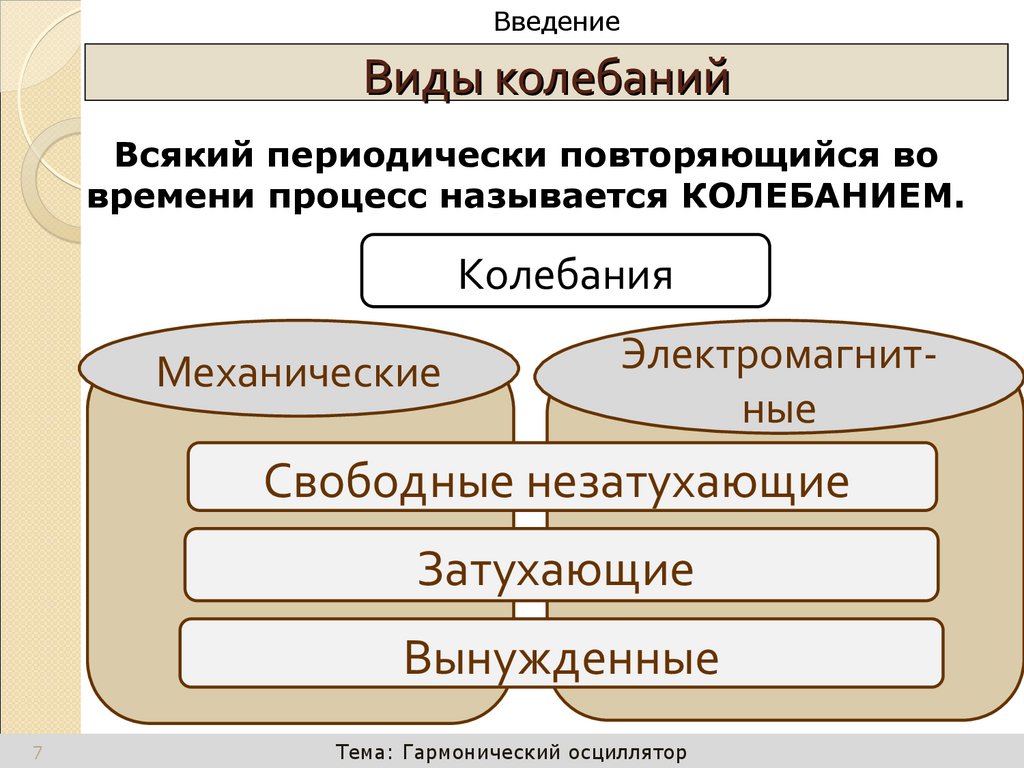
7. Виды колебаний

Динамика поступательного
движения
Введение
Виды колебаний
Всякий периодически повторяющийся во
времени процесс называется КОЛЕБАНИЕМ.
Колебания
Механические
Электромагнитные
Свободные незатухающие
Затухающие
Вынужденные
7
Тема: Гармонический осциллятор

8. 1. Математический маятник

Динамика
поступательного движения
Математический
маятник
1. Математический маятник
Тема: Гармонический осциллятор

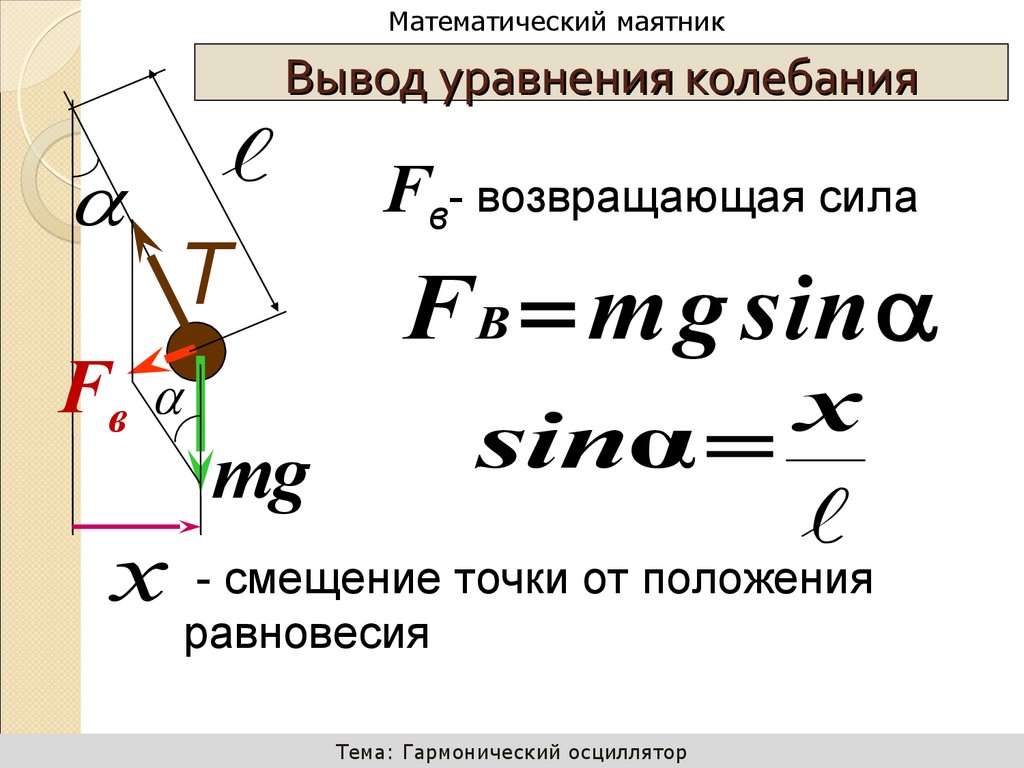
9. Вывод уравнения колебания

Динамика
поступательного движения
Математический
маятник
Вывод уравнения колебания
Т
Fв
Fв- возвращающая сила
F B m g sin
x
sinα
mg
x - смещение точки от положения
равновесия
Тема: Гармонический осциллятор

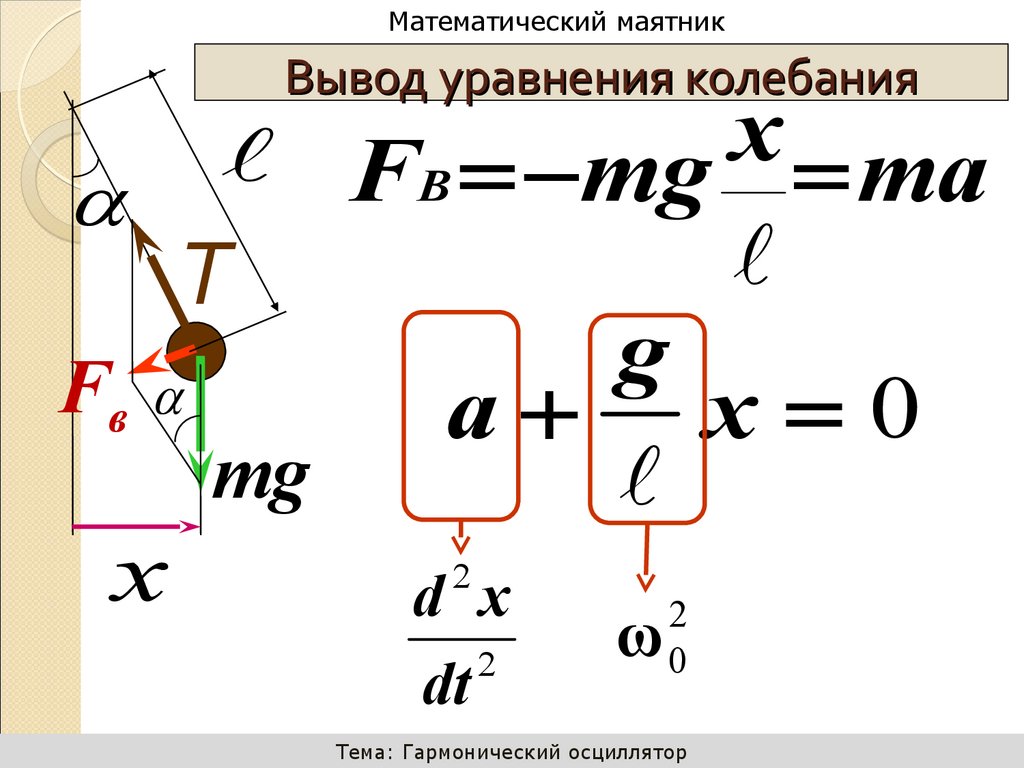
10. Вывод уравнения колебания

Динамика
поступательного движения
Математический
маятник
Вывод уравнения колебания
FB mg x ma
Т
Fв
x
mg
g
a x 0
2
d x
2
dt
ω
2
0
Тема: Гармонический осциллятор

11. Дифференциальное уравнение колебаний

Динамика
поступательного движения
Математический
маятник
Дифференциальное уравнение
колебаний
22
d x
22
ω
x
0
00
22
dt
(1)
Тема: Гармонический осциллятор

12. Период колебаний

Динамика
поступательного движения
Математический
маятник
Период колебаний
2π
2π
T
g
ω0
Тема: Гармонический осциллятор

13. Решение дифференциального уравнения:

Динамика
поступательного движения
Математический
маятник
2. Пружинный маятник
0
Тема: Гармонический осциллятор
x

14. 2. Пружинный маятник

ДинамикаПружинный
поступательного движения
маятник
2. Пружинный маятник
0
x
F= ma = -kx
2
d x k x 0
2
2
dt
m
0
Тема: Гармонический осциллятор

15. 2. Пружинный маятник

ДинамикаПружинный
поступательного движения
маятник
Дифференциальное уравнение
k 2
0
m
d 2 x 2 x 0
0
2
dt
Период колебаний
(2)
m
T 2
k
Тема: Гармонический осциллятор

16. Дифференциальное уравнение

ДинамикаПружинный
поступательного движения
маятник
Решение дифференциального уравнения
Для (1)
и (2)
x A sin( ω 0 t α );
или
x A cos( ω 0 t α 0 )
А - амплитуда смещения 90
0
ВОЗЬМЕМ 2-е УРАВНЕНИЕ И НАЙДЕМ
СКОРОСТЬ, УСКОРЕНИЕ И ВОЗВРАЩАЮЩУЮ
СИЛУ
Тема: Гармонический осциллятор
0

17. Решение дифференциального уравнения

3. Скорость колеблющейся точки
Динамика поступательного
движения
Скорость,
ускорение,
энергия точки
dx
υ
A 0 sin( 0 t 0 )
dt
υmax–
АМПЛИТУДА СКОРОСТИ
Амплитуда – это максимальное
значение колеблющегося параметра
Тема: Гармонический осциллятор

18. 3. Скорость колеблющейся точки

Динамика поступательного
движения
Скорость,
ускорение,
энергия точки
Ускорение колеблющейся точки
dυ
2
a
A 0 cos( 0 t 0 )
dt
а – амплитуда ускорения
max
Тема: Гармонический осциллятор

19. Ускорение колеблющейся точки

Динамика поступательного
движения
Скорость,
ускорение,
энергия точки
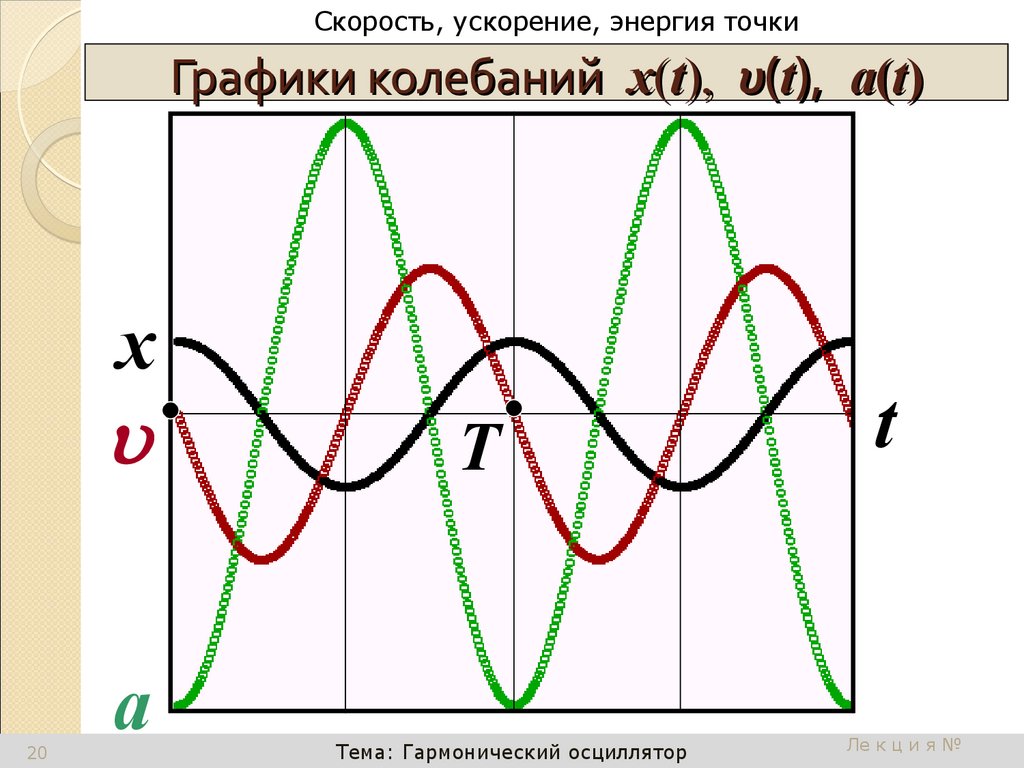
Графики колебаний х(t), υ(t), a(t)
x
20
a
T
Тема: Гармонический осциллятор
t
Ле к ц и я №

20. Графики колебаний х(t), υ(t), a(t)

Динамика поступательного
движения
Скорость,
ускорение,
энергия точки
Возвращающая сила
F ma m A cos( 0 t 0 )
2
0
Fmax – амплитуда силы
Тема: Гармонический осциллятор

21. Возвращающая сила

Динамика поступательного
движения
Скорость,
ускорение,
энергия точки
Энергия колеблющейся точки
• потенциальная
2
2
0
2
mω x
kx
Wп
2
2
1
2 2
2
m ω 0 A сos ( ω 0 t α 0 )
2
Тема: Гармонический осциллятор

22. Энергия колеблющейся точки

Динамика поступательного
движения
Скорость,
ускорение,
энергия точки
Энергия колеблющейся точки
• кинетическая
2
mυ
Wк
2
1
2
2
2
mA ω 0 sin ( ω 0 t α 0 )
2
Тема: Гармонический осциллятор

23. Энергия колеблющейся точки

Динамика поступательного
движения
Скорость,
ускорение,
энергия точки
Полная энергия
2
0
mω A
W Wк Wп
2
W Wк ,max Wп ,max
Тема: Гармонический осциллятор
2

24. Энергия

Динамика поступательного
движения
Скорость,
ускорение,
энергия точки
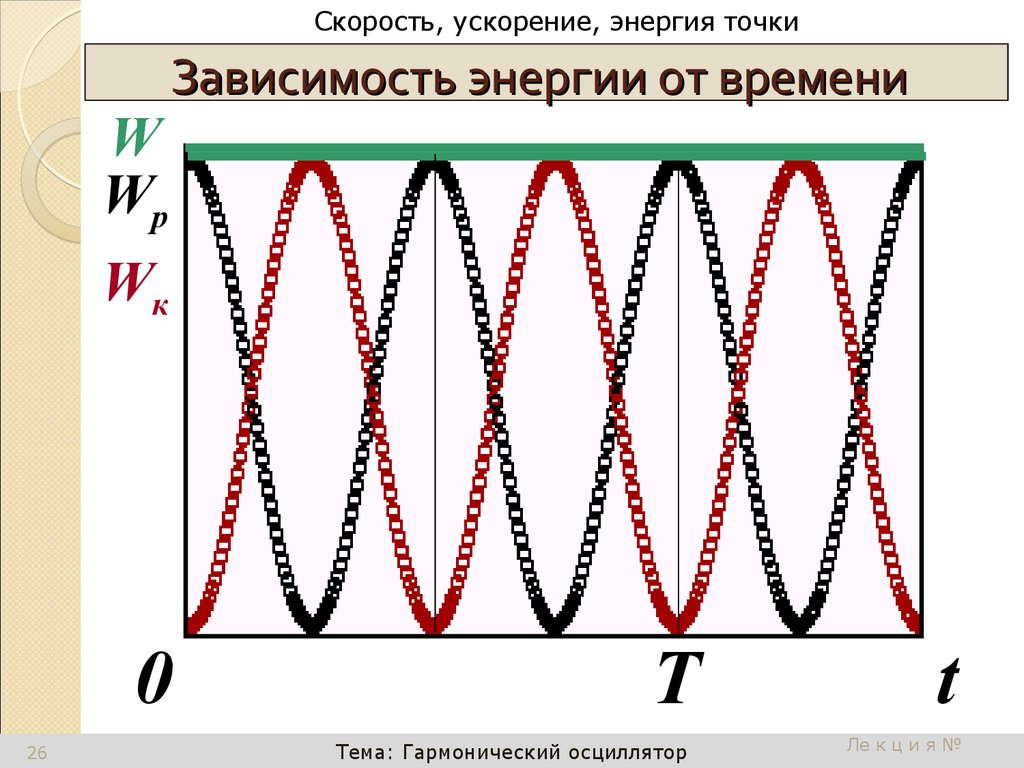
W
Wp
Зависимость энергии от времени
Wк
0
26
T
t
Тема: Гармонический осциллятор
Ле к ц и я №

25. Полная энергия

Динамика
поступательного движения
Математический
маятник
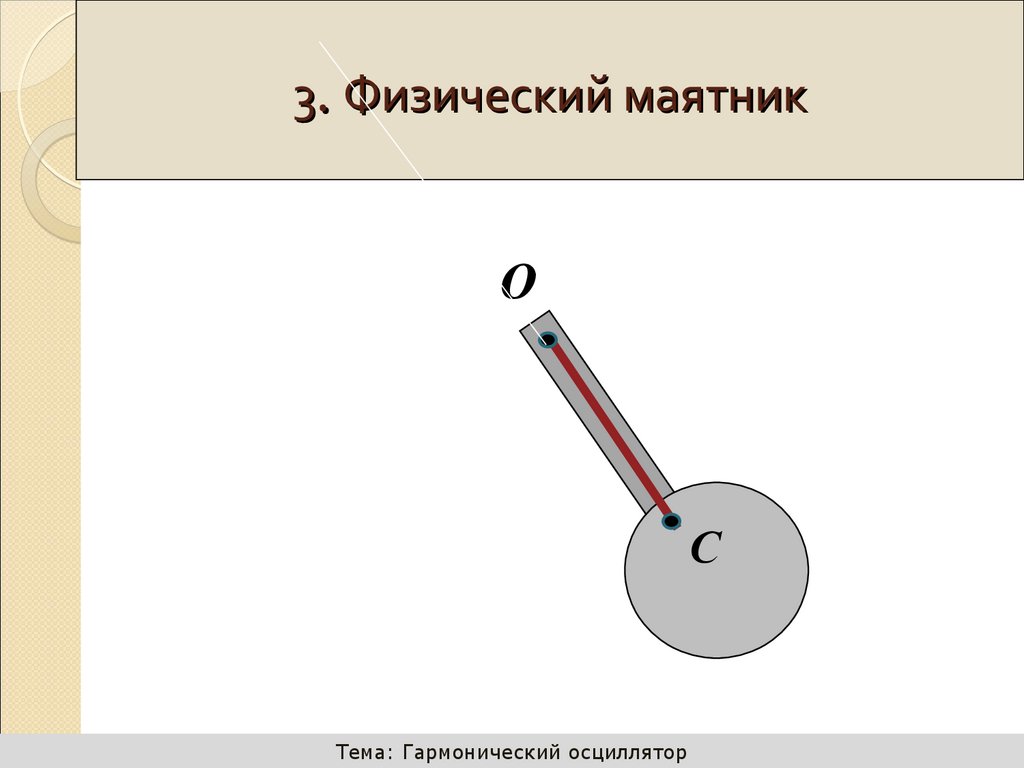
3. Физический маятник
О
С
Тема: Гармонический осциллятор

26. Зависимость энергии от времени

Динамика поступательного
движения
Скорость,
ускорение,
энергия точки
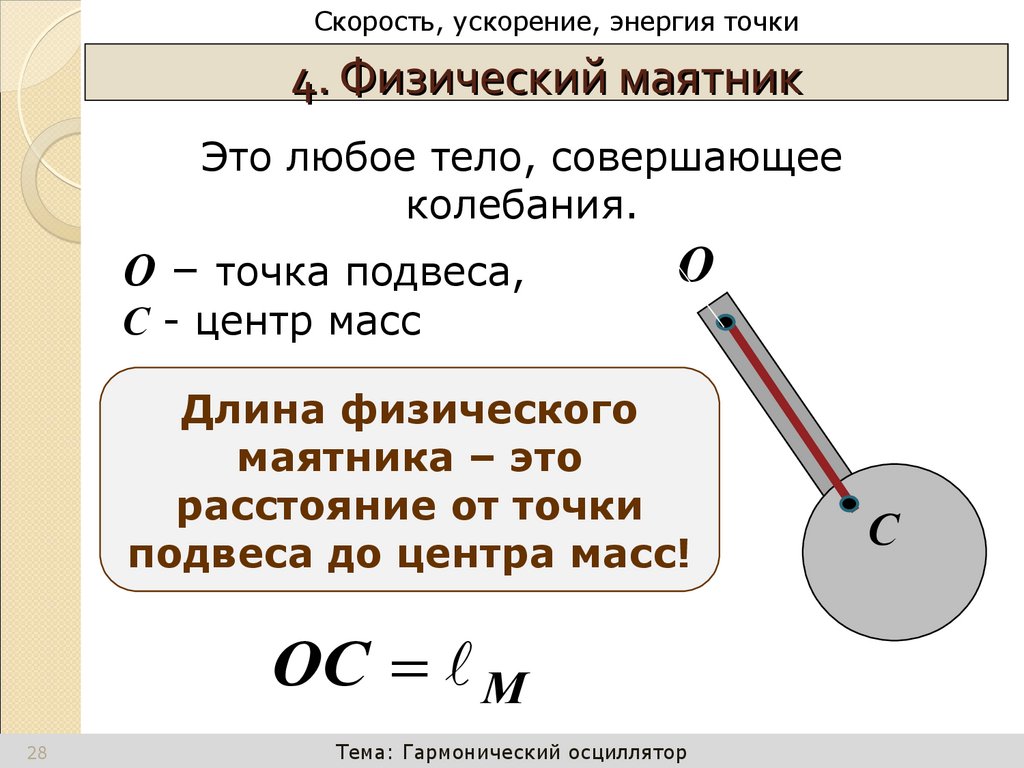
4. Физический маятник
Это любое тело, совершающее
колебания.
О – точка подвеса,
О
С - центр масс
Длина физического
маятника – это
расстояние от точки
подвеса до центра масс!
OC M
28
Тема: Гармонический осциллятор
С

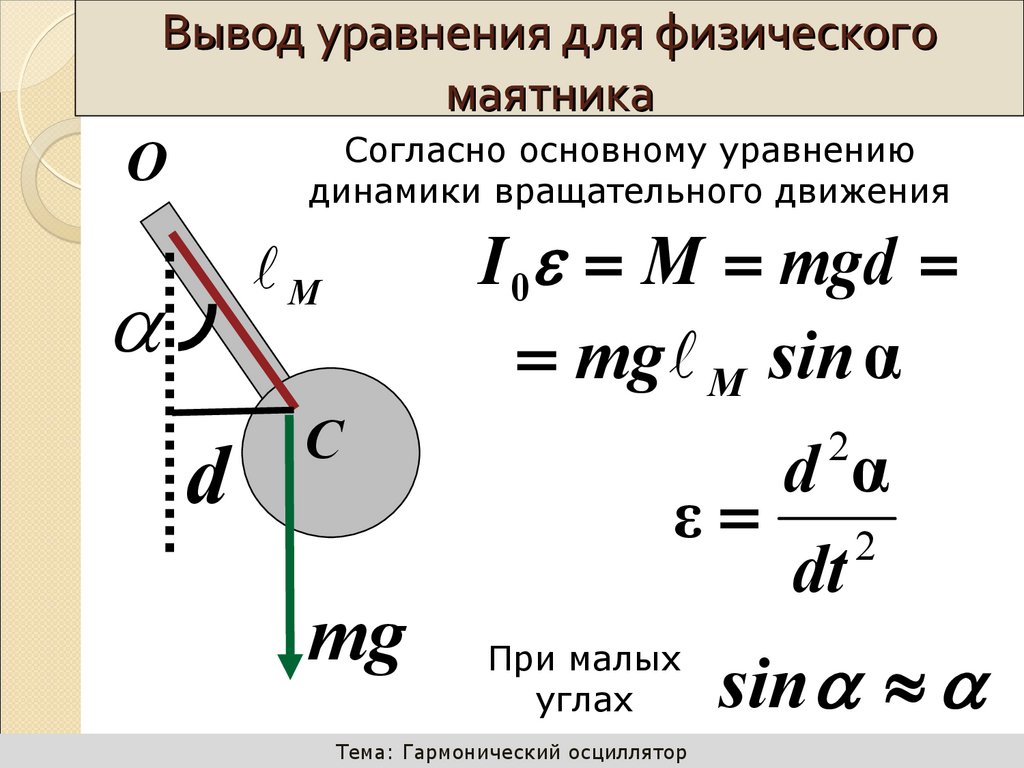
27. 3. Физический маятник

Вывод уравнения для физического
маятника
ДинамикаФизический
поступательного движения
маятник
Согласно основному уравнению
динамики вращательного движения
О
M
d
С
mg
I 0 M mgd
mg M sin α
2
d α
ε 2
dt
При малых
углах
Тема: Гармонический осциллятор
sin

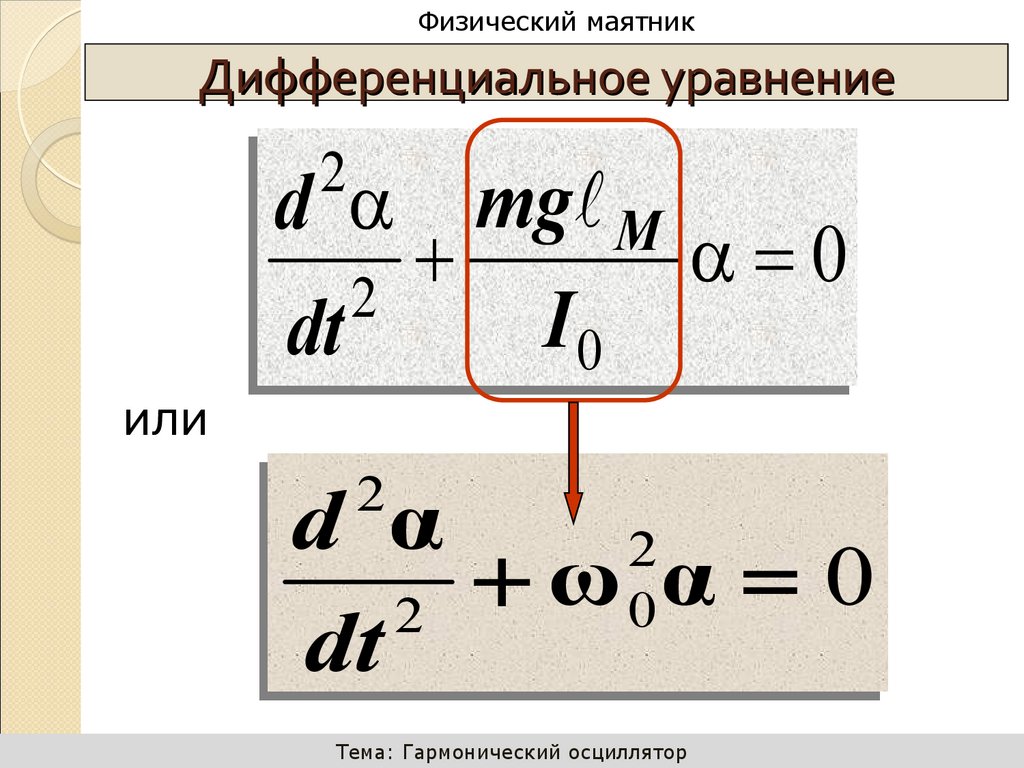
28. 4. Физический маятник

ДинамикаФизический
поступательного движения
маятник
Дифференциальное уравнение
mg MM
d mg
0
0
2
2
dt
II00
dt
2
2
d
или
22
d α
22
ω
α
0
00
22
dt
Тема: Гармонический осциллятор

29. Вывод уравнения для физического маятника

ДинамикаФизический
поступательного движения
маятник
Частота, период, приведенная длина
0
mg M
I0
Приведенная длина
физического маятника
– это длина
математического
маятника с таким же
периодом колебаний,
что и у физического.
I0
T 2π
m M g
I0
пр
m M
Тема: Гармонический осциллятор

30. Дифференциальное уравнение

ДинамикаФизический
поступательного движения
маятник
Приведенная длина физического
маятника
По теореме
Штейнера
2
I 0 I c m M
Ic
пр
M M
m M
Приведенная длина всегда больше длины
физического маятника
Тема: Гармонический осциллятор

31. Частота, период, приведенная длина

Вывод:
ДинамикаФизический
поступательного движения
маятник
1. Дифференциальные уравнения и их
решения имеют одинаковый вид для
всех маятников:
2
2
d x
d x
2
2
x
0
x
0
0
0
2
2
dt
dt
22
dd αα
22
ω
α
0
ω
α
0
00
22
dt
dt
2. Циклическая
частота (и
период) зависит
от параметров
колебательной
системы
Тема: Гармонический осциллятор