Что такое СРС?

1.

Сегодня: пятница, 13 июня 2025 г.
ЛЕКЦИЯ 1 (часть 1)

2. Курс: Физика. Оптика. Атомная физика группы ИВТ-11, 12, 13, 14; УТС-11, 12

Особенность курса:
• ВСЯ «Общая физика» - за 1 год
(1 курс, 1-й/2-й семестры)
Аудиторная нагрузка – 64/80 час
Самостоятельная
работа студентов - 80/100! час

3.

ЧТО ТАКОЕ СРС ?
САЙТ А.Н.ВАРГИНА, где есть все учебники!!!
1. https://www.ph4s.ru/catalog/fizika/obshchaya-fizika-dlyastudentov-mladshikh-kursov/
2. https://www.ph4s.ru/about/
2. [Электронный ресурс].-М.: Коллекция электронных
ресурсов МИЭТ
Режим доступа: https://orioks.miet.ru/
3. Программа обучения. «Открытая Физика 2.6. Часть2»:
http://www.physics.ru/courses/op25part2/design/index.htm
4. Диск «Физика в анимациях»
5. Переписка со старостами групп

4.

1.
2.
3.
4.
5.
6.
7.
Основная литература:
Савельев И. В. Курс общей физики, кн. 4., кн.5 – М.: ООО
«Издательство Астрель», ООО «Издательство АСТ», 2004.
И. Е. Иродов. Волновые процессы. Основные законы: Учебное
пособие для вузов.- М.: Бином. Лаборатория знаний, 2007.
И. Е. Иродов. Квантовая физика. Основные законы: Учебное
пособие для вузов.- М.: Бином. Лаборатория знаний, 2007.
Иродов И. Е. Задачи по общей физике. – М.: ЗАО
«Издательство БИНОМ», 2007.
Лосев В.В., Морозова Т.В. Оптика. Лабораторный практикум по
курсу общей физики. «Оптика» - М.: МИЭТ, 2008. (Часть 1,
часть 2).
Берестов А.Т., Боргардт Н.И., Куклин С.Ю. Лабораторные
работы по курсу общей физики «Строение вещества». - М.:
МИЭТ, 2007.
Калашников Н.П., Кожевников Н.М. Физика. Интернет
тестирование Базовых знаний: учебное пособие. – СПб.:
Лань, 2009. – 160 с.

5. Бально-накопительный регламент

«Удовлетвори
тельно»
50 - 69
«Хорошо»
«Отлично»
70 - 85
86-100
При
условии,
что за экз.
тест
получено
не менее 6
баллов
Подробно см. файл: 1-НС ИВТ УТС 2025.doc

6.

Тема 1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
1.1. Виды и признаки колебаний
1.2. Характеристики (параметры)
гармонических колебаний
1.3. Гармонический осциллятор
1.4. Энергия гармонических колебаний
СРС 1.5. Примеры уравнения динамики
гармонических колебаний.
Математический и физический маятники

7.

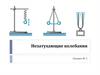
Примеры колебательных процессов
Круговая
волна
на
поверхности
жидкости,
возбуждаемая
точечным
источником (гармонически
колеблющимся шариком).
Генерация акустической
волны громкоговорителем.

8.

1.1. Виды и признаки колебаний
В физике особенно выделяют колебания двух
видов – механические и электромагнитные и их
электромеханические комбинации
Три признака колебательного движения:
повторяемость (периодичность) – движение
по одной и той же траектории туда и обратно;
ограниченность пределами крайних положений;
действие
т.н.
квазиупругой
силы,
описываемой функцией F = – kx.
Стремится вернуть систему в состояние равновесия.
Прямо пропорциональна отклонению от положения
равновесия.

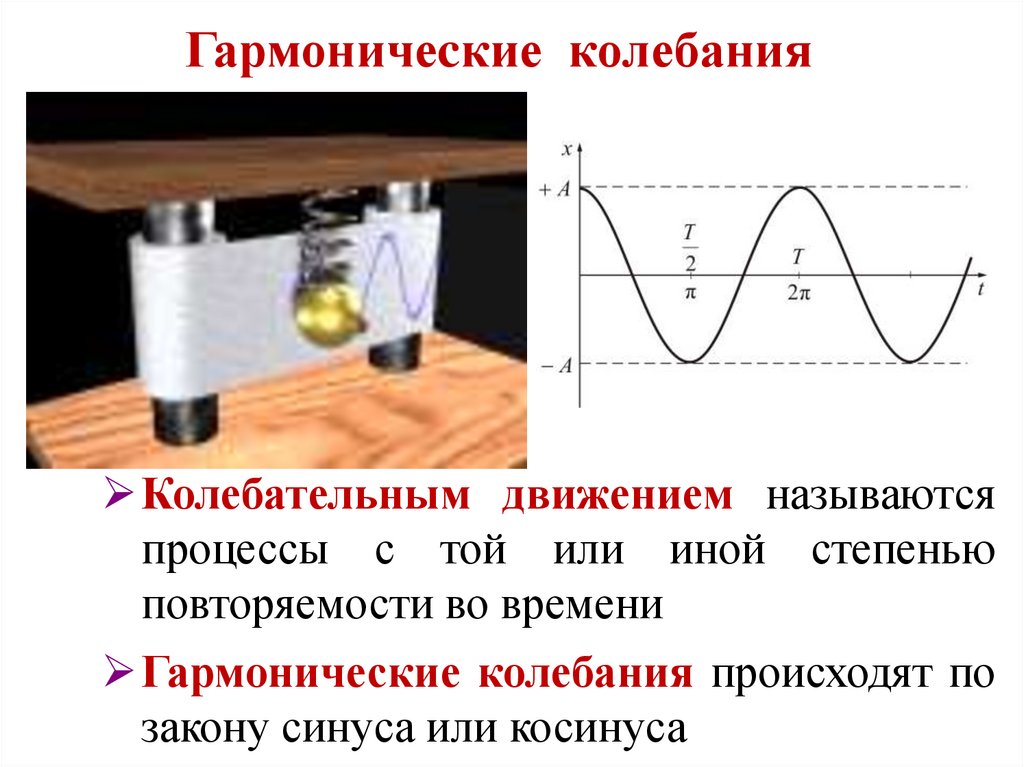
9. Гармоничеcкие колебания

Колебательным движением называются
процессы с той или иной степенью
повторяемости во времени
Гармонические колебания происходят по
закону синуса или косинуса

10.

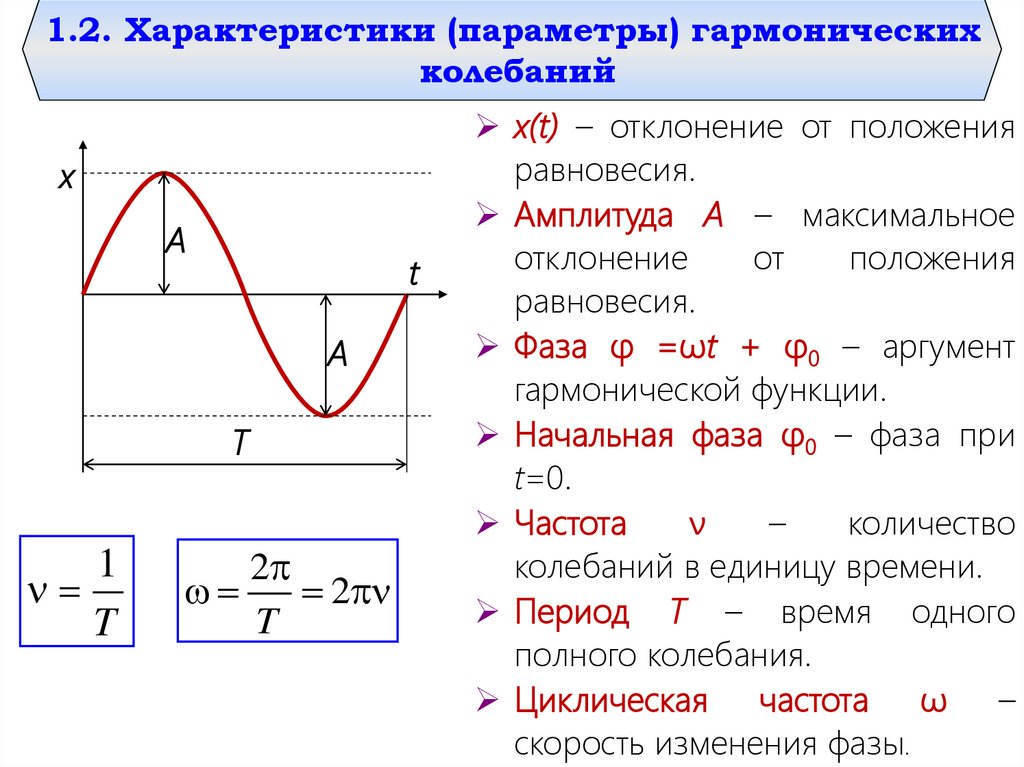
1.2. Характеристики (параметры) гармонических
колебаний
x
А
t
А
T
1
T
2
2
T
x(t) – отклонение от положения
равновесия.
Амплитуда A – максимальное
отклонение
от
положения
равновесия.
Фаза φ =ωt + φ0 – аргумент
гармонической функции.
Начальная фаза φ0 – фаза при
t=0.
Частота
ν
–
количество
колебаний в единицу времени.
Период T – время одного
полного колебания.
Циклическая частота ω –
скорость изменения фазы.

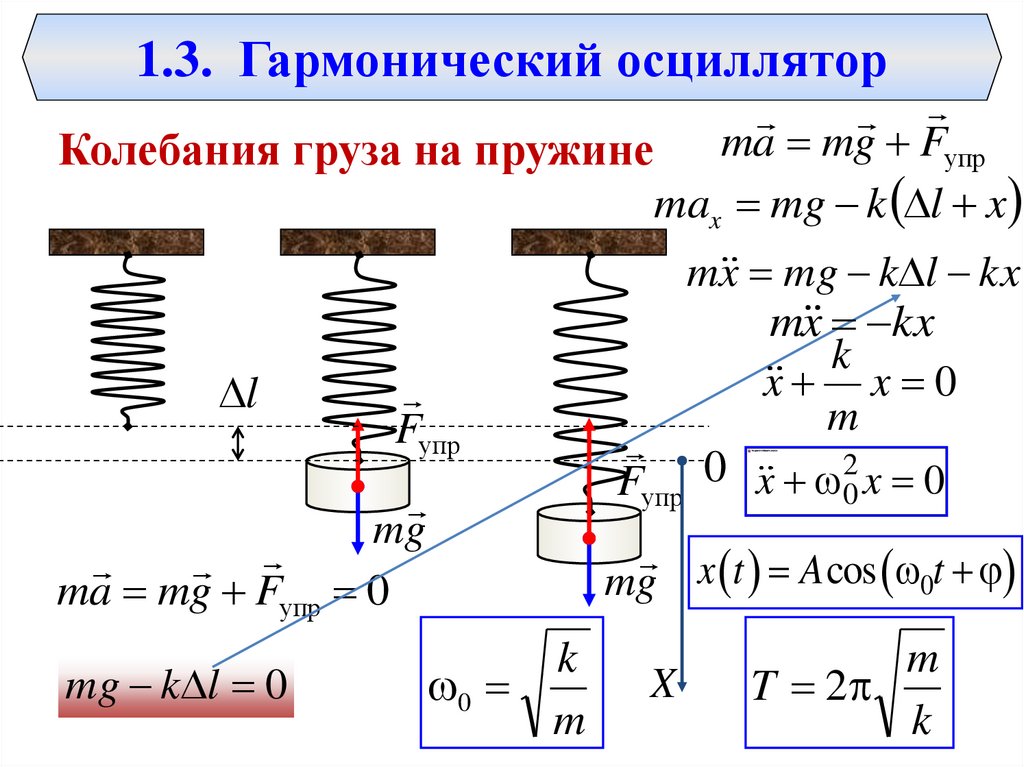
11. Колебания груза на пружине

1.3. Гармонический осциллятор
Колебания груза на пружине ma mg Fупр
max mg k l x
l
Fупр
mg
ma mg Fупр 0
mg k l 0
m x mg k l kx
m x kx
k
x x 0
m
Fупр 0 x 02 x 0
x t A cos t
0
mg
k
0
m
X
m
T 2
k

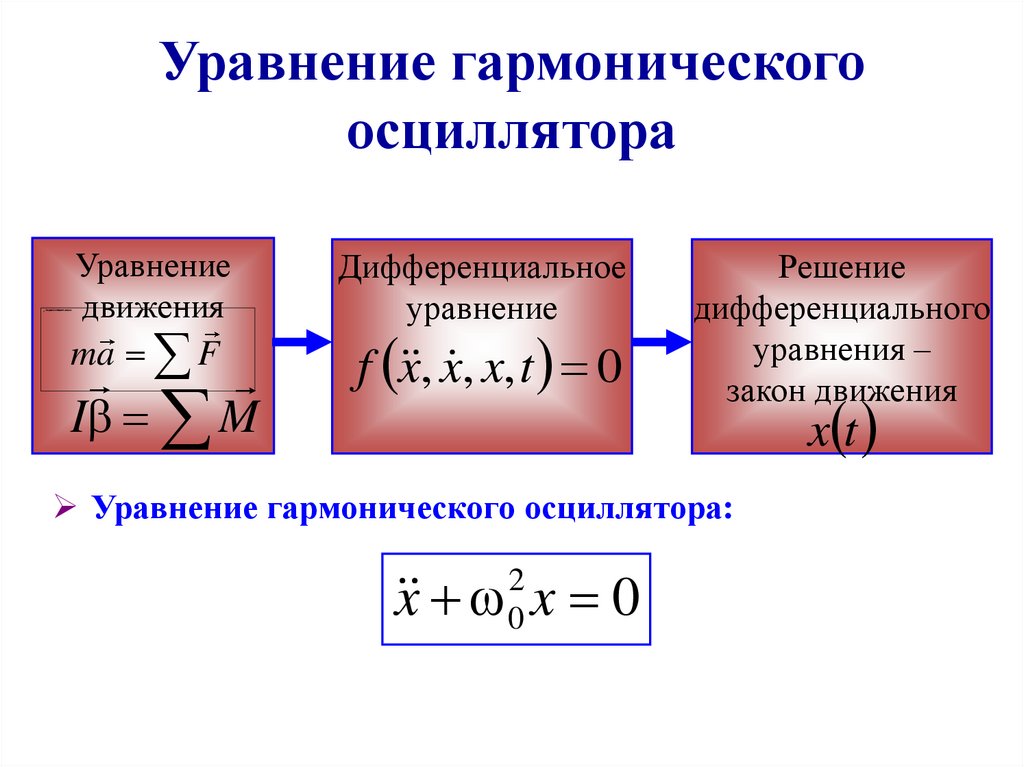
12. Уравнение гармонического осциллятора

Уравнение
движения
ma F
I M
Дифференциальное
уравнение
f x , x , x, t 0
Решение
дифференциального
уравнения –
закон движения
Уравнение гармонического осциллятора:
x x 0
2
0
x t

13. Решение уравнения гармонического осциллятора

x 02 x 0
Решение уравнения гармонического осциллятора
(гармонический закон движения):
x t A cos 0t
Другие формы записи:
x t A sin 0t
x t A sin 0t B cos 0t
Комплексная форма:
x t ei 0t
Формула Эйлера: e i 0t cos 0t i sin 0t

14.

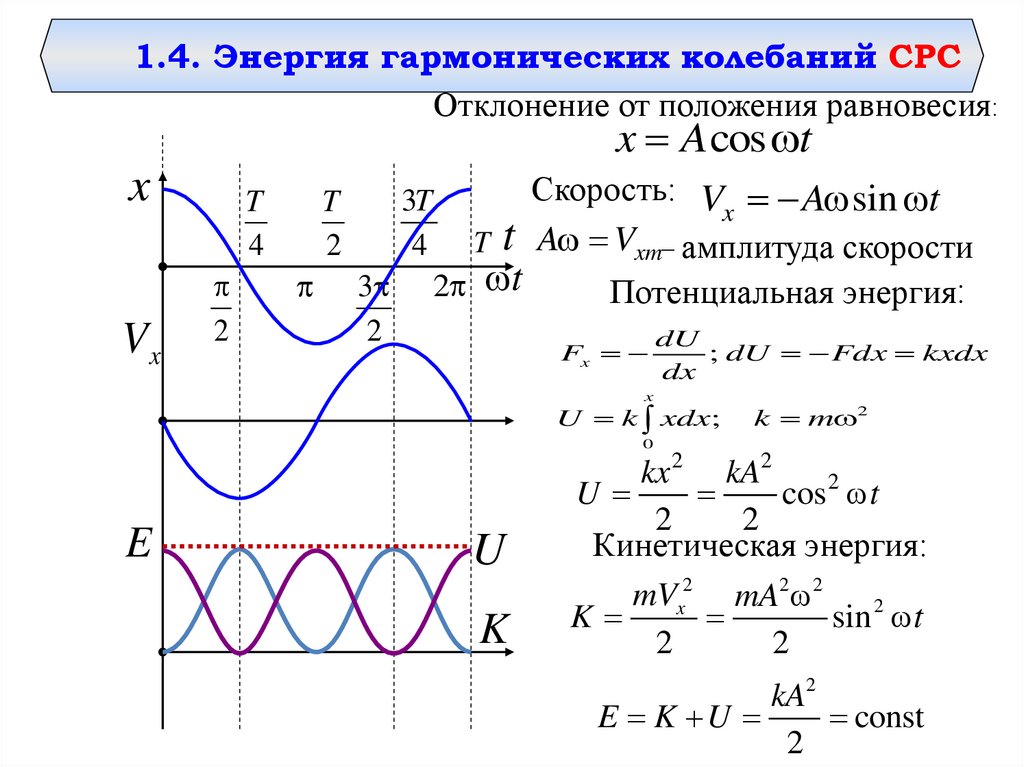
1.4. Энергия гармонических колебаний СРС
Отклонение от положения равновесия:
x A cos t
x
Vx
T
4
2
3T
4
T
2
3
2
Скорость: V A sin t
x
T t A Vxm– амплитуда скорости
2 t
Потенциальная энергия:
Fx
x
dU
; dU Fdx kxdx
dx
U k xdx;
k m 2
0
E
U
K
kx 2 kA2
U
cos 2 t
2
2
Кинетическая энергия:
mVx2 mA2 2
K
sin 2 t
2
2
kA2
E K U
const
2

15.

СРС 1.5. Примеры уравнения динамики
гармонических колебаний.
Математический и физический маятники
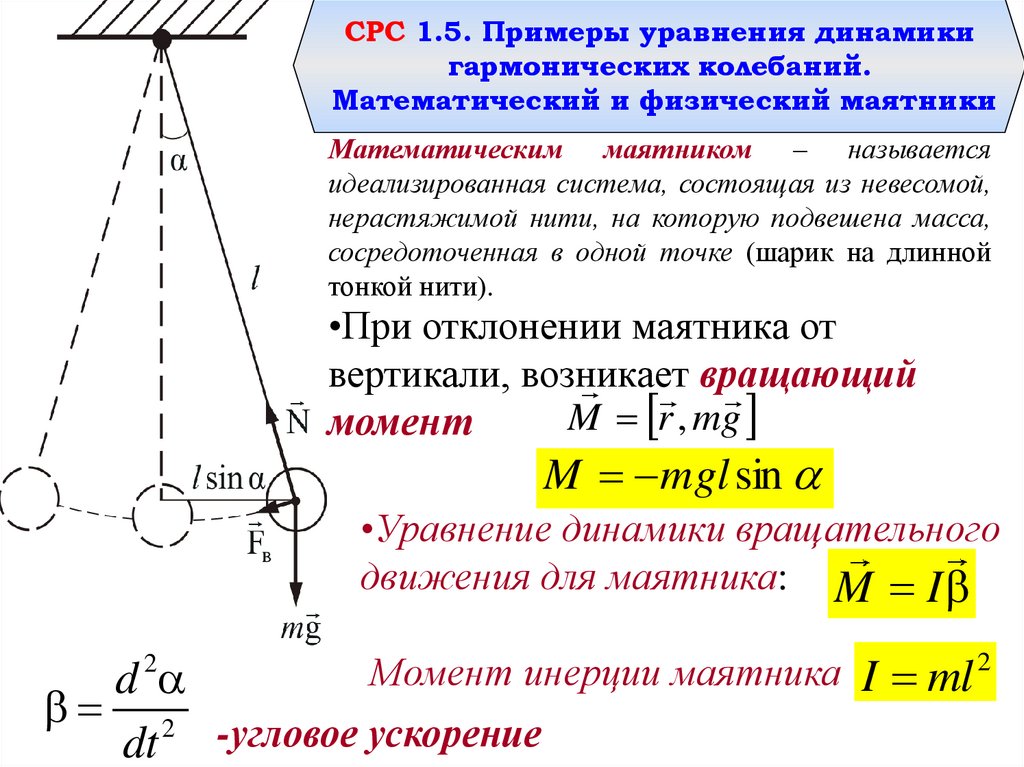
Математическим маятником – называется
идеализированная система, состоящая из невесомой,
нерастяжимой нити, на которую подвешена масса,
сосредоточенная в одной точке (шарик на длинной
тонкой нити).
•При отклонении маятника от
вертикали, возникает
вращающий
M r , mg
момент
M mgl sin
•Уравнение динамики вращательного
движения для маятника: M I
Момент инерции маятника I ml 2
d
2
dt -угловое ускорение
2

16.

2
d
2
Тогда ml
mgl sin , или
2
dt
g
2
sin .
0
Обозначим :
l
2
d
2
Уравнение движения маятника
0 0
2
dt
- Это уравнение динамики гармонических колебаний.
Решение уравнения (1.6.3) имеет вид:
m cos( 0t )
0
g
l
l
T 2
g
Т – зависит только от длины маятника и ускорения
свободного падения.

17.

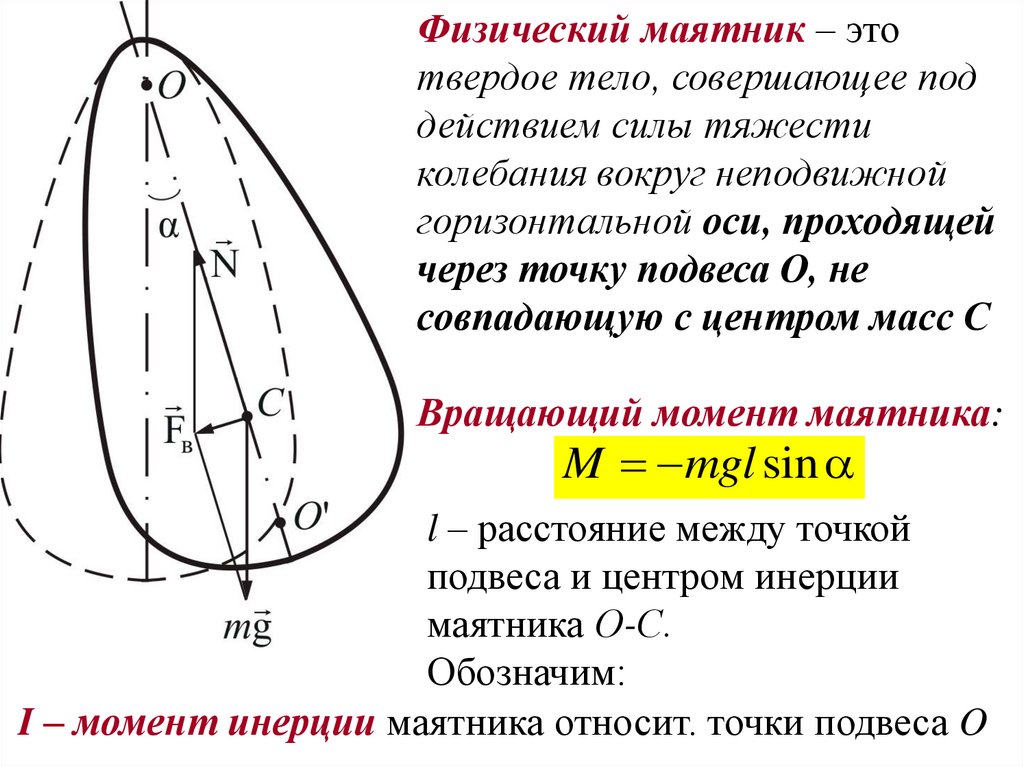
Физический маятник – это
твердое тело, совершающее под
действием силы тяжести
колебания вокруг неподвижной
горизонтальной оси, проходящей
через точку подвеса О, не
совпадающую с центром масс С
Вращающий момент маятника:
M mgl sin
l – расстояние между точкой
подвеса и центром инерции
маятника О-С.
Обозначим:
I – момент инерции маятника относит. точки подвеса O

18.

d 2
d 2 - угловое ускорение, тогда
I 2 mgl sin
2
dt
dt
sin
Уравнение динамики вращательного движения
d
2
0 0
2
dt
2
m cos( 0t )
где
I
lпр.
I
mgl
T 2
T 2
lпр.
mgl
ml
g
I
lпр. – приведенная длина физического маятника – это длина такого
2
0
математического маятника, период колебания которого совпадает с
периодом колебаний данного физического маятника.

19.

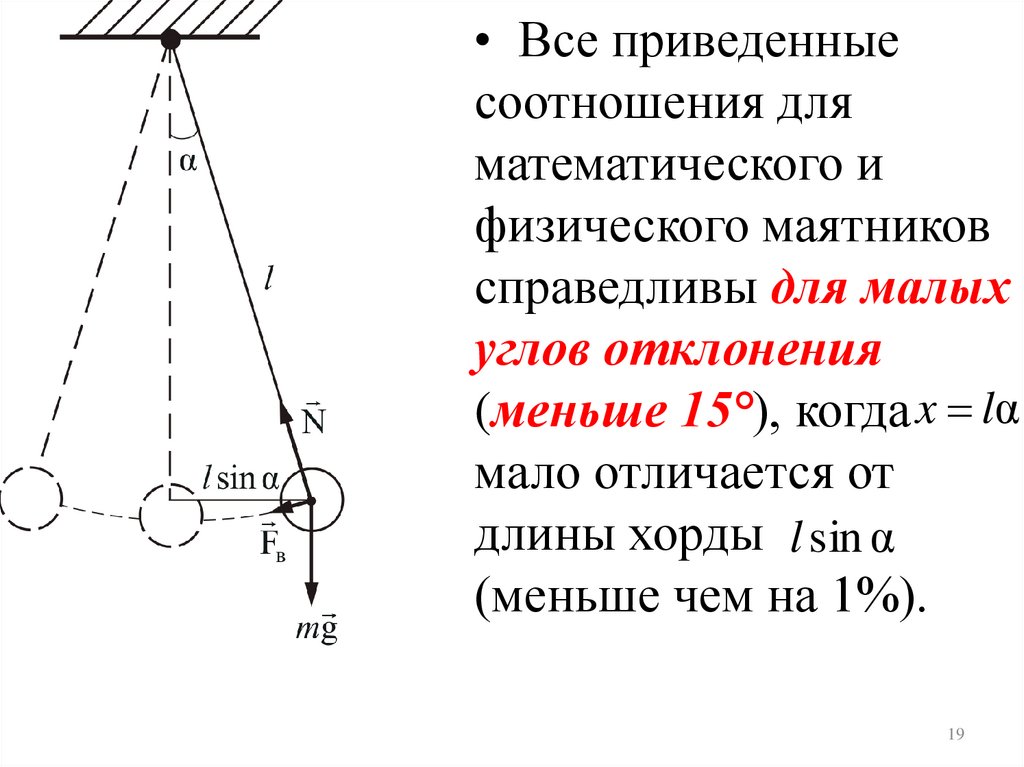
• Все приведенные
соотношения для
математического и
физического маятников
справедливы для малых
углов отклонения
(меньше 15°), когда x lα
мало отличается от
длины хорды l sin α
(меньше чем на 1%).
19