Similar presentations:
02.03.16 Формулы сокращенного умножения(1)
1.
Классная работа 11.02.26Формулы сокращенного
умножения.
2.
Формулы сокращённогоумножения
Разность квадратов:
a b a b a b
2
2
3.
Устно:• Представить в виде куба:
3
8х
6
64с
12
b
4.
Устно:• Представить в виде куба:
3
27х =
6
8b =
9
y =
5.
Устно:• Представить в виде куба:
64 у3 =
1 3
b =
125
а12b9 =
27 n6m15 =
6.
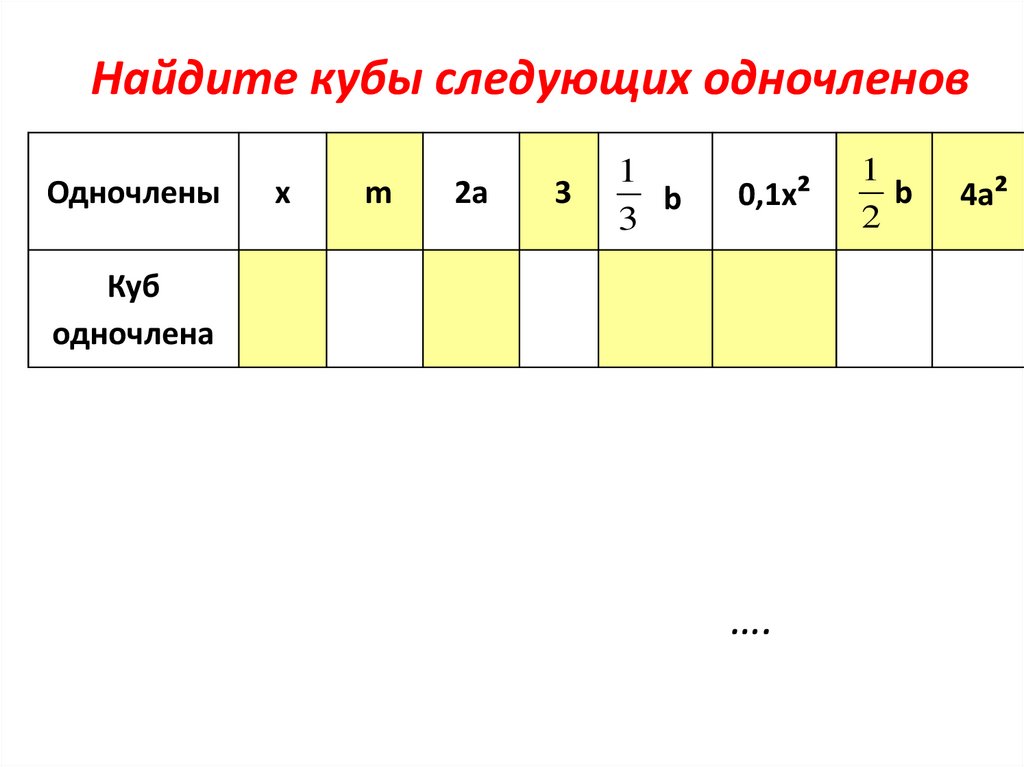
Найдите кубы следующих одночленовОдночлены
x
m
2a
3
1
b
3
0,1x²
Куб
одночлена
….
1
b
2
4a²
7.
Формула суммы кубовa b (a b) (a ab b )
3
3
2
Сумма кубов двух выражений равна произведению
суммы этих выражений и неполного квадрата их
разности.
2
8.
Алгоритм разложения cуммы кубовна множители:
1.Представить двучлен в виде суммы
кубов.
2.Выполнить разложение по формуле
а3+в3= (а + в)(а2 - aв + b2) сумма кубов
Пример:
27 + m3= (3)3+ m3=(3 + m)((3)2 – 3*m+
m2) = (3 + m)(9- 3m +m2)
9.
Формула разности кубовa b (a b) (a ab b )
3
3
2
Разность кубов двух выражений равна
произведению разности этих выражений и
неполного квадрата их суммы.
2
10.
Алгоритм разложения разности кубовна множители:
1.Представить двучлен в виде разности
кубов.
2.Выполнить разложение по формуле
а3-в3= (а- в)(а2+ aв + b2) разность кубов
Пример:
64а6- 8b9=(4a2)3 - (2b3)3 =(4a2 – 2b3)((4a2)2+
4a2*2b3 +(2b3)2)=(4a2- 2b3)(16a4+ 8a2b3+4b6
)
11.
Формулы:a³ + b³ = (a + b) (a² - ab + b²)
Сумма
кубов
Сумма
выражений
Неполный квадрат
их разности
a³ - b³ = (a - b) (a² + ab + b²)
Разность
кубов
Разность
выражений
Неполный квадрат
их суммы
12.
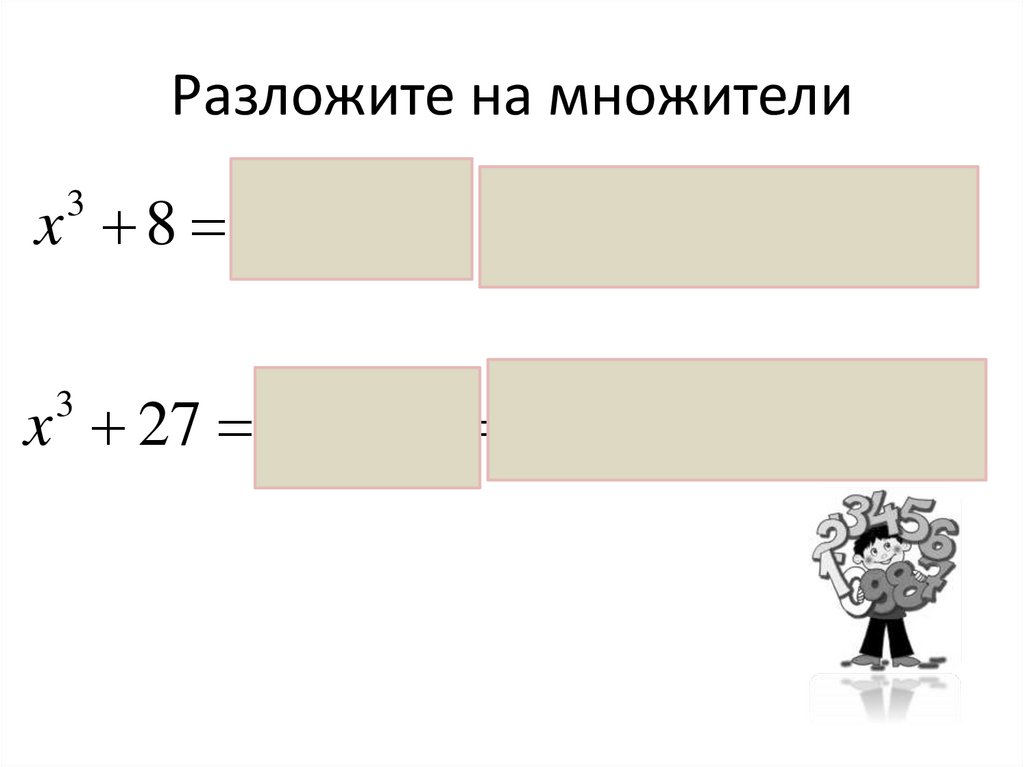
Разложите на множителиx 8 x 2 ( x 2)( x 2 x 4)
3
3
3
2
x 27 x 3 ( x 3)( x 3 x 9)
3
3
3
2
13.
27 + b³ = 3 ³ + b³ = (3 + b)(3² - 3b + b²)a³ - 8c³ = a³ - (2с)³ = (a – 2с)(a² + 2aс + (2с )²)
….
14.
Разложит е на множит ели:a 8
3
b 27
3
216 m
3
64 a 1
3
a b 1
1 3 8 3
a b
8
27
3 3










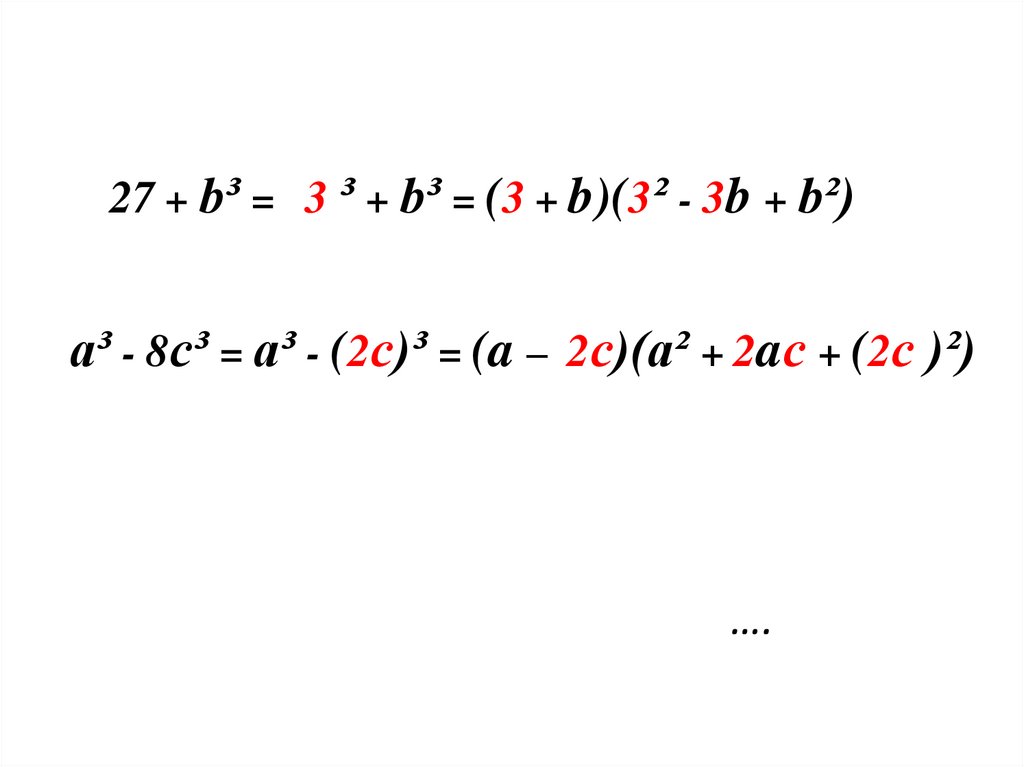

 mathematics
mathematics








