Similar presentations:
Разложение на множители суммы и разности кубов
1.
а b3
а b
3
06.04.2020
3
3
1
2. Цели урока:
• вывести формулы суммы иразности кубов; формировать
умение применять их при
разложении многочлена на
множители
3. Устно:
• Представить в виде куба:3
8х
6
64с
12
b
2х
3
4с
b
2 3
4 3
4. Устно:
• Представить в виде куба:3
5
у
•1
3
х
3
•27 x
3
3 2 3
а
b
9
6
а b
3
2
5
8n6y15 2n y
3
125у
5. Устно:
• Выполните возведение в квадрат.2
4
x
4
x
1
2
(2x – 1)
n)2
81 18 x n
2
(9 –
2
25
30
a
9
a
2
(–3a + 5)
2
1 a2 a 1
a
4
2
6.
• Для разложения на множители суммыкубов используют тождество
а b (a b)(a ab b )
3
3
2
• - формула суммы кубов
• Докажем ее.
2
7.
(a b)(a ab b )3
2
2 2
2
3
a a b ab a b ab b
3
3
a b
2
2
8.
а b (a b)( a ab b )3
3
2
2
• Сумма кубов двух
выражений равна
произведению суммы этих
выражений на неполный
квадрат разности
9. Пример:
22
Пример:
а b (a b)( a ab b )
3
3
• Разложите на
множители:
0,027 x 1 0,3 x 1
2
0,3 x 1 (0,3 0,3 x 1)
0,3x 1 (0,09 0,3x 1)
3
3
3
10.
• Для разложения на множителиразности кубов используют
тождество
а b (a b)( a ab b )
3
3
2
• - формула разности кубов
• Докажем ее.
2
11.
(a b)(a ab b )3
2
2 2
2
3
a a b ab a b ab b
3
3
a b
2
2
12.
а b (a b)( a ab b )3
3
2
2
• Разность кубов двух
выражений равна
произведению разности
этих выражений на
неполный квадрат суммы.
13. Пример:
а b (a b)( a ab b )Пример:
3
3
2
2
• Разложите на множители:
x y x y
2
2
2
2 2
x y x xy y
2
2
2
4
x y x xy y
3
6
3
2 3
14. Упражнения:
Упражнения:
№ 905
№ 907
№ 909 (а, в, д)
№ 911
№ 912 (а, в, д)
№ 914
15. Итоги урока:
• – Назовите формулы суммы иразности кубов.
• – Когда применяются эти
формулы?
• – Какие ещё формулы позволяют
разложить многочлен на
множители? Назовите их.






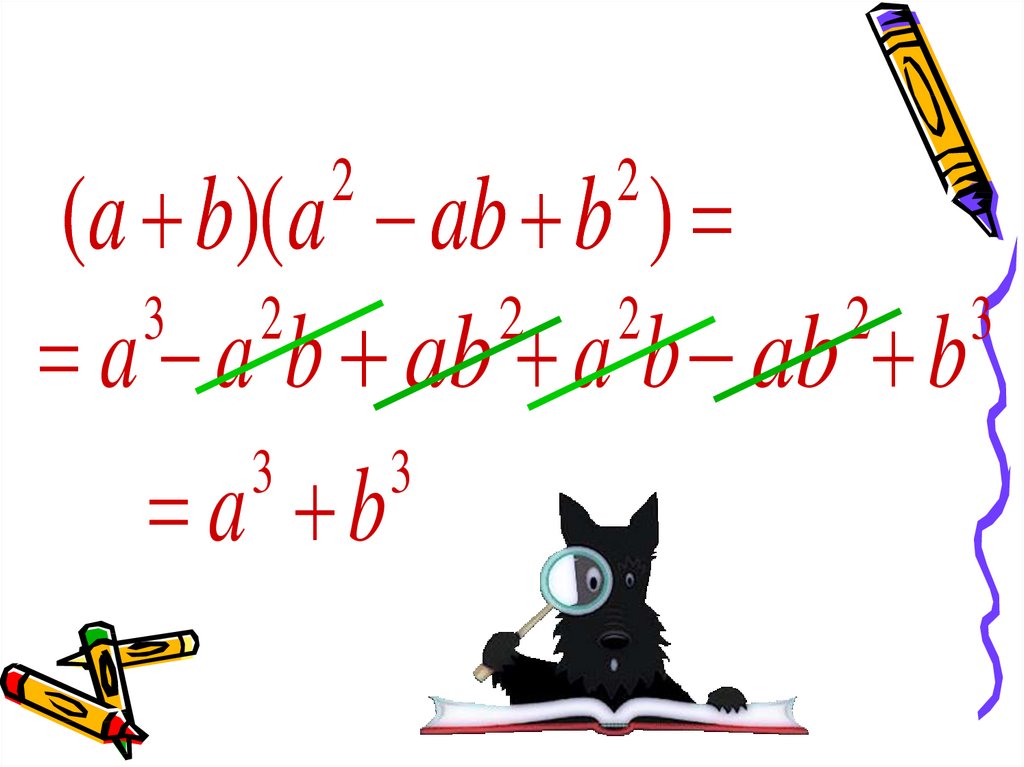

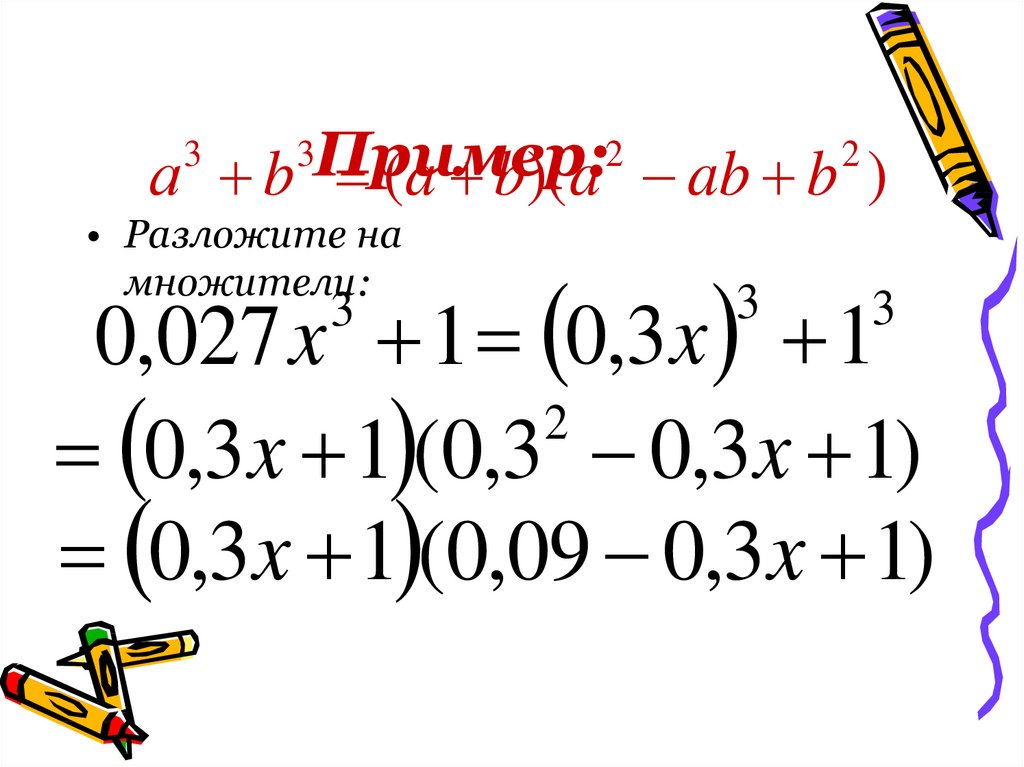

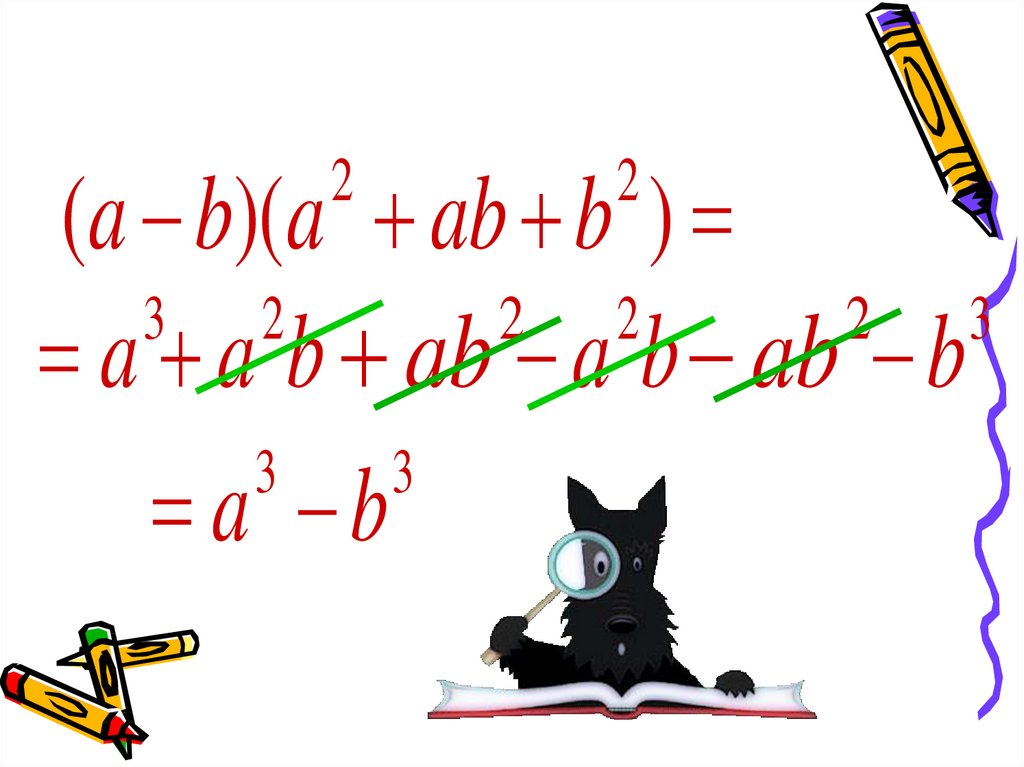

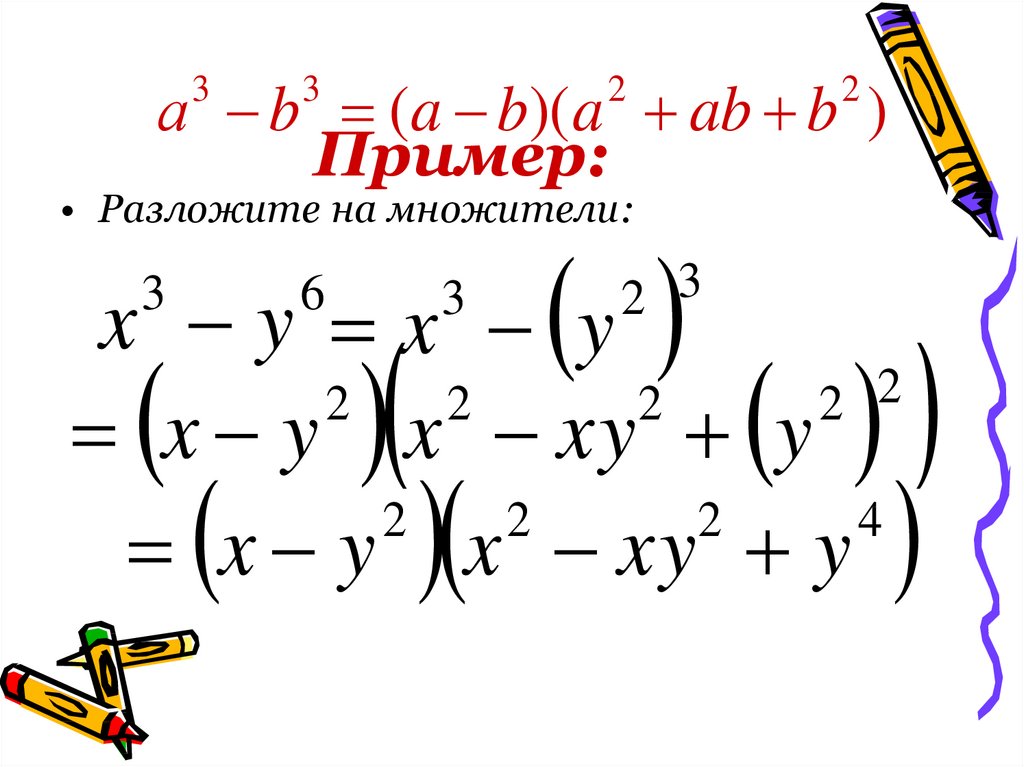


 mathematics
mathematics








