Энергия

1. ЭНЕРГИЯ. РАБОТА. ЗАКОНЫ СОХРАНЕНИЯ ЭНЕРГИИ

2.

Работа – это физическая величина,
характеризующая процесс превращения одной
формы движения в другую.
Элементарная работа dA, совершаемая силой F,
равна скалярному произведению силы на
элементарное перемещение точки приложения
силы dr:
dA=Fdr
Работа на конечном
перемещении равна
r
интегралу
A12 Fdr F r cos
r
где Δr – перемещение точки, α – угол между F и
Δr. Если при этом перемещение происходит
по
прямолинейной траектории, то r s12 где s12 –
пройденный точкой путь. Тогда
А12=Fs12cosα
2
1

3.

Сила, действующая на материальную точку, не
совершает работы, если:
А) точка покоится
Б) При α = 90° работа, совершаемая силой, равна нулю.
Работа может быть вычислена графически:
1) Если Fs =const. Работа силы на пути s12 численно
равна площади прямоугольника
2) Если Fs ≠const. Работа силы на пути s12 численно
равна площади криволинейной трапеции.
Работа – алгебраическая величина, она может быть
положительна и отрицательная.

4.

Мощность N– это физическая величина,
равная отношению работы A к
промежутку времени t, в течение которого
совершена эта работа.
Средняя за промежуток времени Δt
мощность равна <N>=A12/Δt
Мгновенная мощность равна производной
работы по времени N=dA/dt.
Учитывая, что dr/dt=v, получим
N=Fdr/dt=Fv.
Мгновенная мощность равна скалярному
произведению силы на скорость.

5.

Силы, работа которых не зависит от формы
пути, по которому материальная точка
переходит из некоторого начального
положения в конечное, называются
консервативными или потенциальными
(сила тяжести). A1a2 = A1b2
Сила называется неконсервативной или
непотенциальной, если совершаемая ею
работа зависит от формы пути (сила тяги,
сила трения). Работа на замкнутой
траектории A = A1a2 + A2b1 = A1a2 – A1b2 = 0

6.

В качестве единой количественной меры
различных форм движения материи (работы) и
соответствующих им взаимодействий вводится
скалярная величина – энергия.
Физическая величина, равная половине
произведения массы тела на квадрат его скорости,
называется кинетической энергией тела:
mv2
Eк
2
Работа приложенной к телу равнодействующей
силы равна изменению его кинетической энергии.
A Eк 2 Eк1
Это утверждение называют теоремой о
кинетической энергии.

7.

Свойства кинетической энергии:
1. Ек однозначна, непрерывна, конечна,
дифференцируемая функция
механического состояния предмета.
2. Ек не может быть отрицательна.
3. Ек аддитивная величина.
4. Изменение Ек равно работе всех сил
действующих на тело.
5. Тело обладающее Ек способно
передавать её другим телам, т.е.
совершать работу.

8.

Потенциальная энергия тела поднятого над
Землей, если на него действуют сила тяжести
равна:
E p mgh
Равна работе, которую совершает сила тяжести
при опускании тела на нулевой уровень.
Работа силы тяжести равна изменению
потенциальной энергии тела, взятому с
противоположным знаком.
A ( E p 2 E p1 )
Физический смысл имеет не сама потенциальная
энергия, а ее изменение при перемещении тела из
одного положения в другое. Это изменение не
зависит от выбора нулевого уровня.

9.

Свойства потенциальной энергии:
1. Еп однородная, непрерывная,
конечная, дифференцируемая
функция механического состояния
объекта.
2. Еп может быть только взаимной
(энергия взаимодействия).
3. Еп может быть как положительная,
так и отрицательная, в зависимости
от начального уровня.
4. Работа есть убыль Еп.

10.

Сумма кинетической и потенциальной энергии
тел, составляющих замкнутую систему и
взаимодействующих между собой посредством
сил тяготения и сил упругости, остается
неизменной.
Eк1 E p1 Eк 2 E p 2
Это утверждение выражает закон сохранения
энергии в механических процессах.
E Eк1 Eк1
называют полной механической энергией.

11.

Закон сохранения импульса: если геометрическая
сумма внешних сил действующих на систему
равна нулю (система замкнута), то импульс
системы сохраняется, то есть не меняется со
временем.
n
Pi const
i 1
Закон сохранения импульса можно применять:
1. Если внешние силы ничтожно малы по
сравнению с внутренними силами (взрывы
снарядов).
2. Если проекция внешних сил на какое-либо
направление равна нулю

12.

Момент импульса замкнутой
механической системы сохраняется.
В замкнутой системе суммы моментов
импульса всех тел системы в любые
два момента времени одинаковы:
n
/
Li Li
n
i 1
i 1

13. Общие свойства жидкостей и газов

14.

В простейшей модели жидкость (или даже газ)
предполагается несжимаемыми и идеальными (т. е.
без внутреннего трения между движущимися
слоями). При движении идеальной жидкости не
происходит превращения механической энергии во
внутреннюю, поэтому выполняется закон
сохранения механической энергии.
Несжимаемой
считается
жидкость,
плотность которой постоянна (ρ = const).

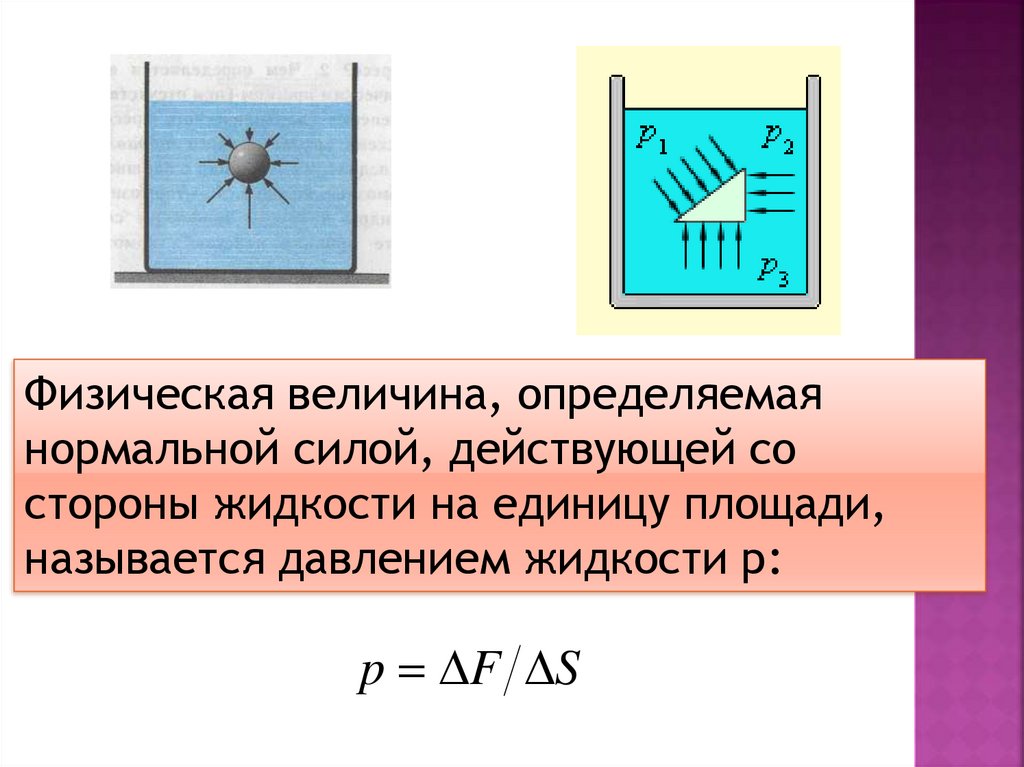
15.

Физическая величина, определяемая
нормальной силой, действующей со
стороны жидкости на единицу площади,
называется давлением жидкости р:
p F S

16.

Единица измерения давления паскаль (Па): 1
Па равен давлению, создаваемому силой 1 Н,
равномерно распределенной по нормальной к
поверхности площади 1 м2, 1 Па = 1 Н/м2.
Внесистемные единицы измерения давления:
кг
9,8 Н
5
1 ат 1 2 1 4 2 10 Па
см
10 м
1 бар 105 Па

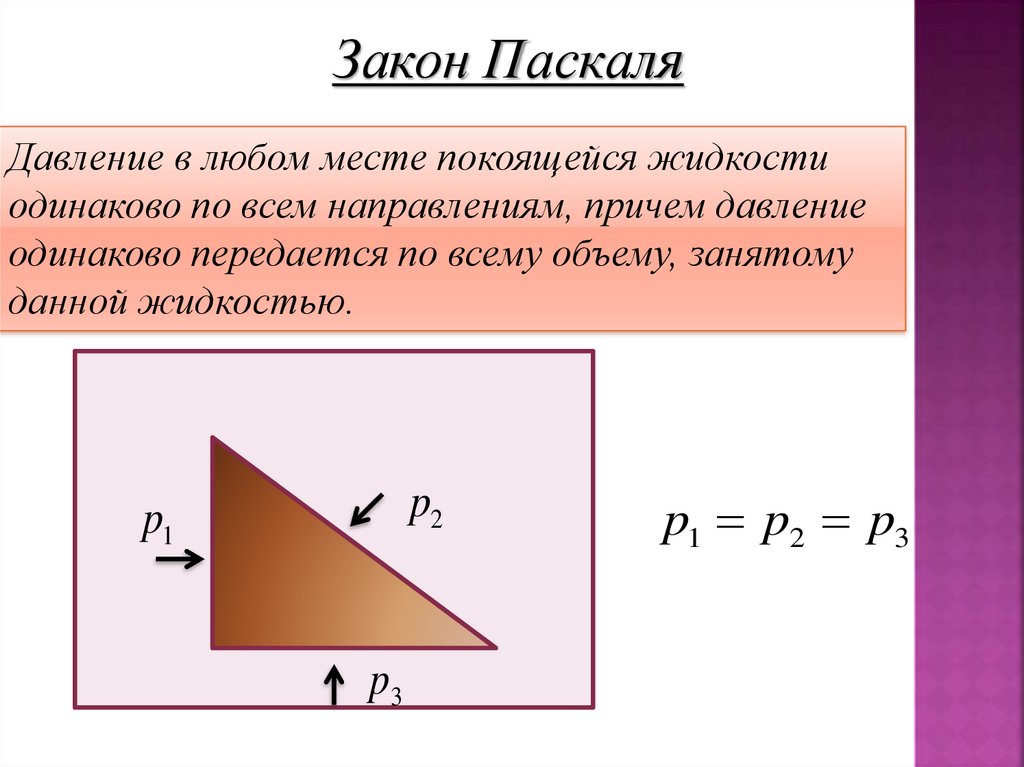
17.

Закон Паскаля
Давление в любом месте покоящейся жидкости
одинаково по всем направлениям, причем давление
одинаково передается по всему объему, занятому
данной жидкостью.
p2
p1
p3
p1 p2 p3

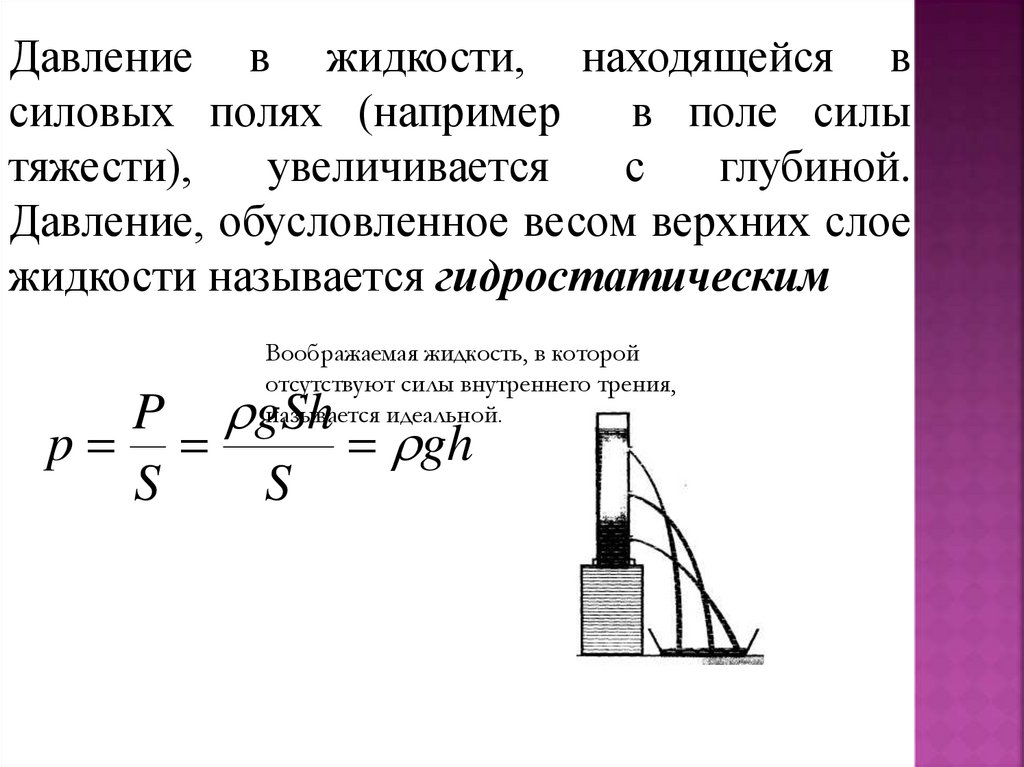
18.

Давление в жидкости, находящейся в
силовых полях (например
в поле силы
тяжести),
увеличивается
с
глубиной.
Давление, обусловленное весом верхних слое
жидкости называется гидростатическим
Воображаемая жидкость, в которой
отсутствуют силы внутреннего трения,
называется идеальной.
P gSh
p
gh
S
S

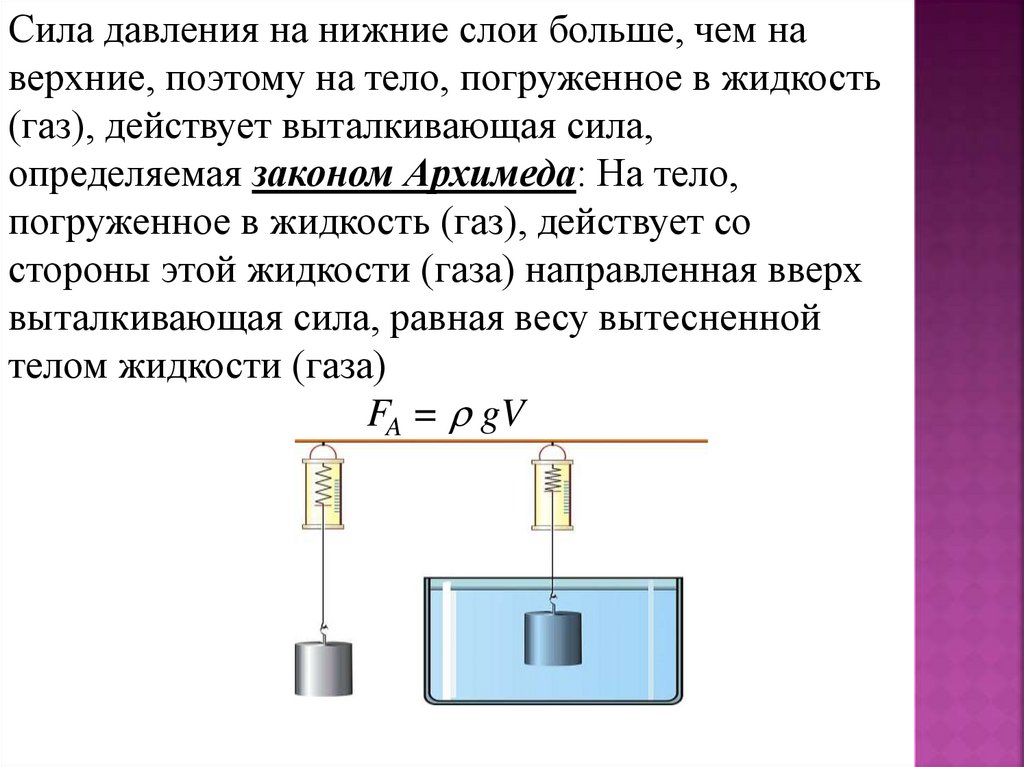
19.

Сила давления на нижние слои больше, чем на
верхние, поэтому на тело, погруженное в жидкость
(газ), действует выталкивающая сила,
определяемая законом Архимеда: На тело,
погруженное в жидкость (газ), действует со
стороны этой жидкости (газа) направленная вверх
выталкивающая сила, равная весу вытесненной
телом жидкости (газа)
FA = gV

20.

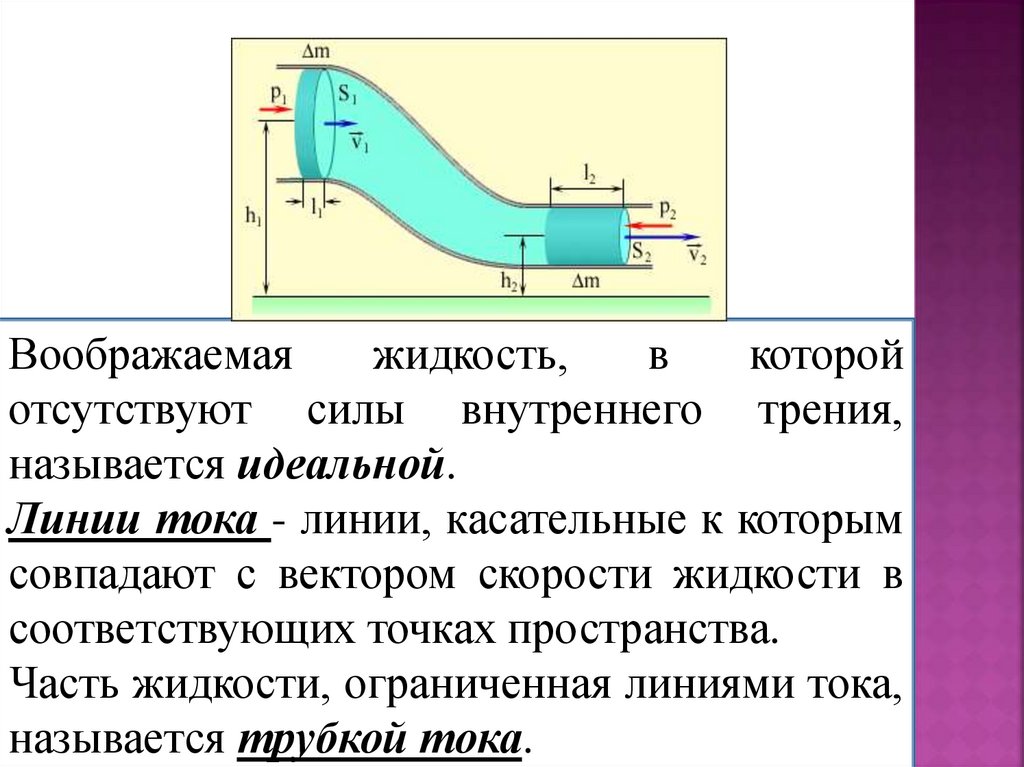
Воображаемая
жидкость,
в
которой
отсутствуют силы внутреннего трения,
называется идеальной.
Линии тока - линии, касательные к которым
совпадают с вектором скорости жидкости в
соответствующих точках пространства.
Часть жидкости, ограниченная линиями тока,
называется трубкой тока.

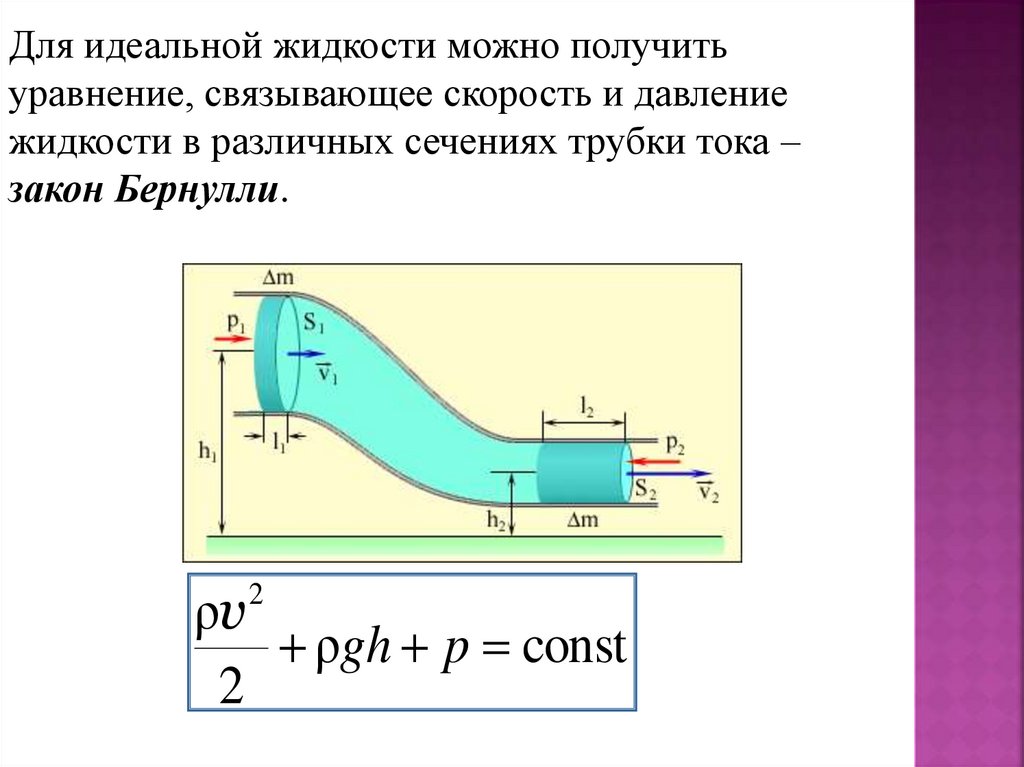
21.

Для идеальной жидкости можно получить
уравнение, связывающее скорость и давление
жидкости в различных сечениях трубки тока –
закон Бернулли.
ρv
ρgh p const
2
2

22.

Уравнение Бернулли выражает закон сохранения
энергии применительно к установившемуся
течению идеальной жидкости:
Для горизонтальной трубки тока (h1 = h2):
ρv
p const
2
2

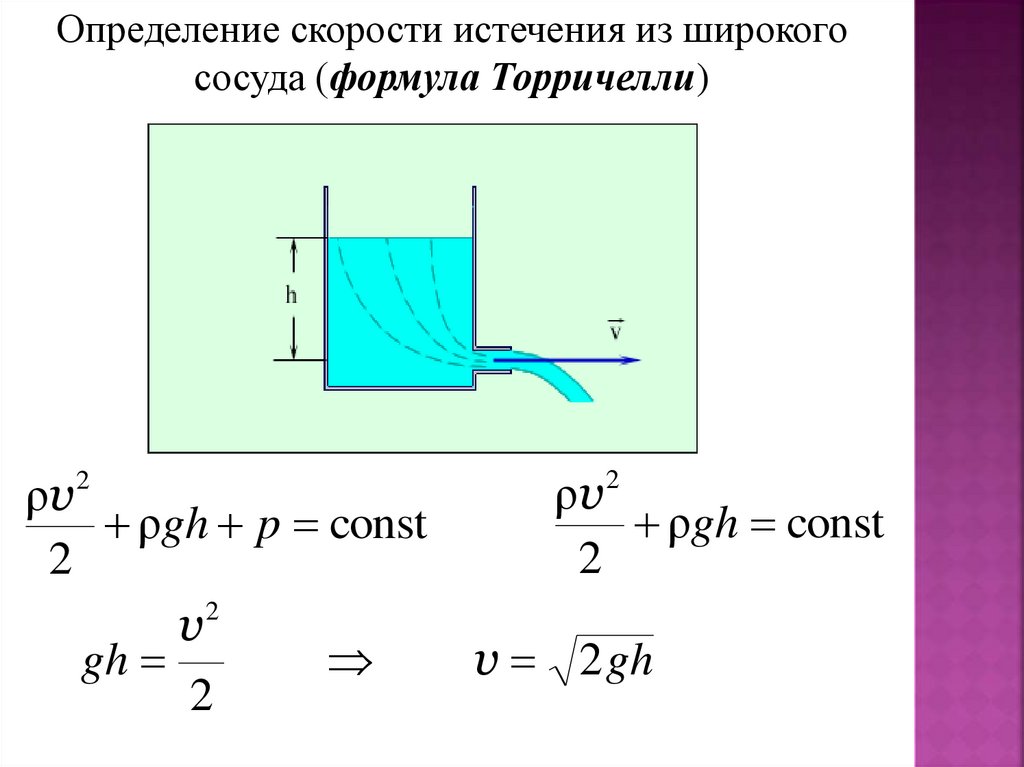
23.

Определение скорости истечения из широкого
сосуда (формула Торричелли)
ρv
ρv
ρgh const
ρgh p const
2
2
2
v
gh
v 2 gh
2
2
2

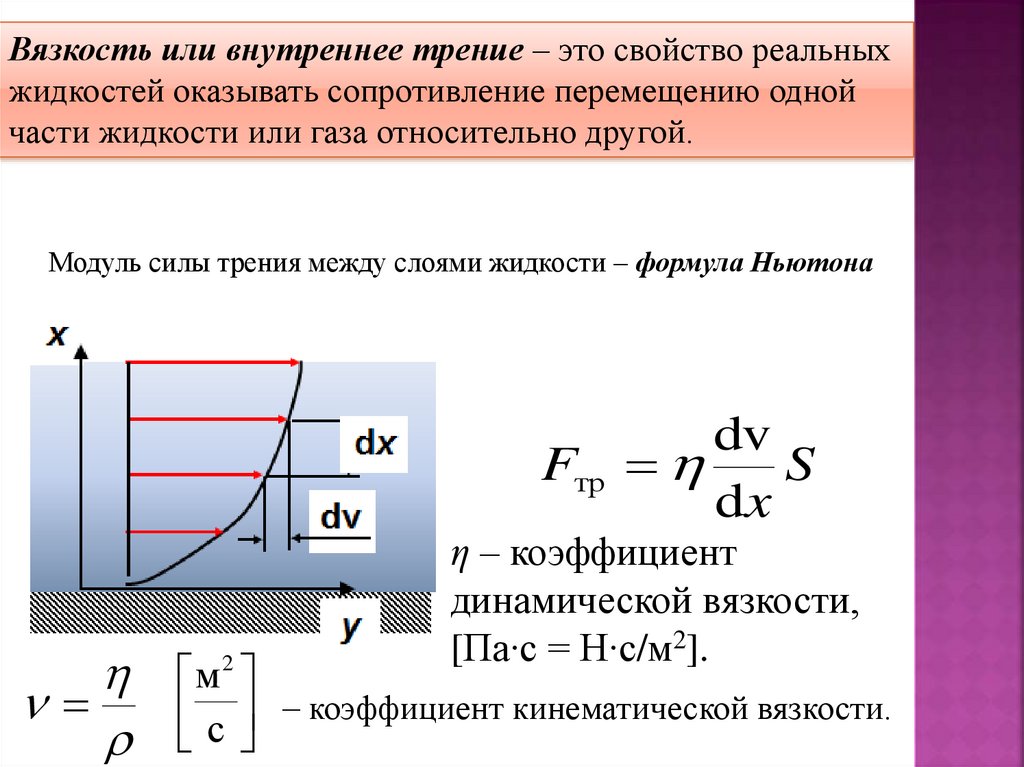
24.

Вязкость или внутреннее трение – это свойство реальных
жидкостей оказывать сопротивление перемещению одной
части жидкости или газа относительно другой.
Модуль силы трения между слоями жидкости – формула Ньютона
dv
Fтр
S
dx
η – коэффициент
динамической вязкости,
[Па∙с = Н∙с/м2].
м2
с коэффициент кинематической вязкости.

25.

26.

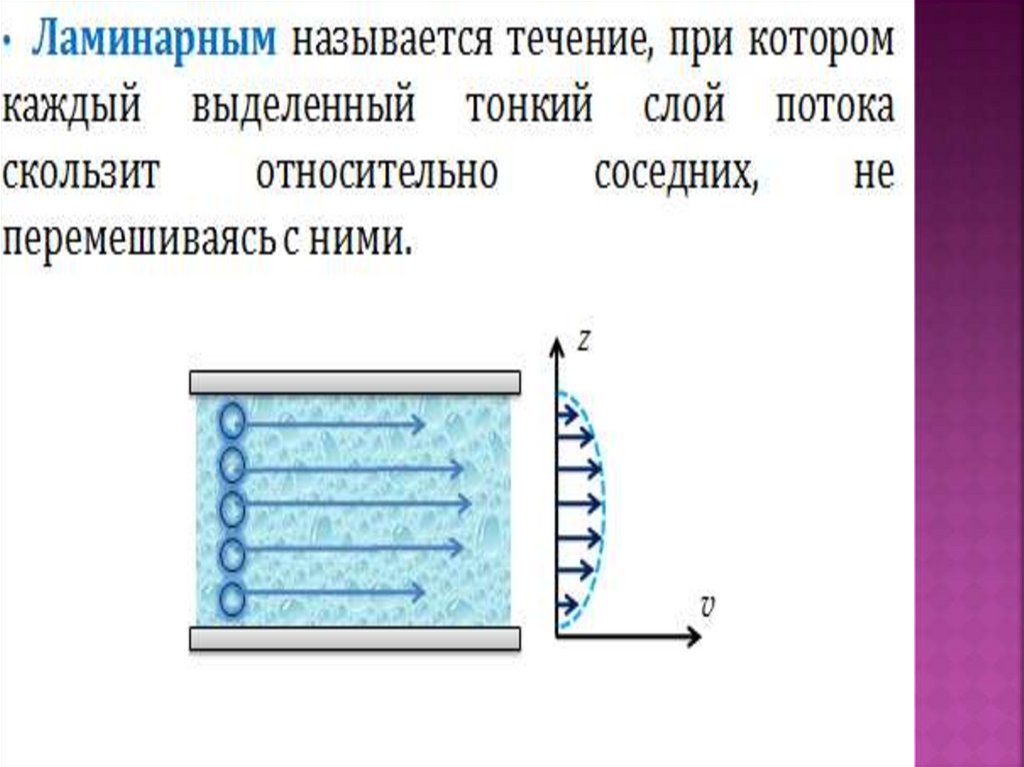
27. Ламинарное течение

Обтекание кругового
цилиндра однородным потоком
жидкости при Re = 0,16.
Для визуализации течения воды
применен алюминиевый
порошок.
Обтекание прямоугольного
выступа на пластинке в лотке
Хилл-Шоу. Краска в потоке
масла выявляет линии тока
плоского потенциального
обтекания.

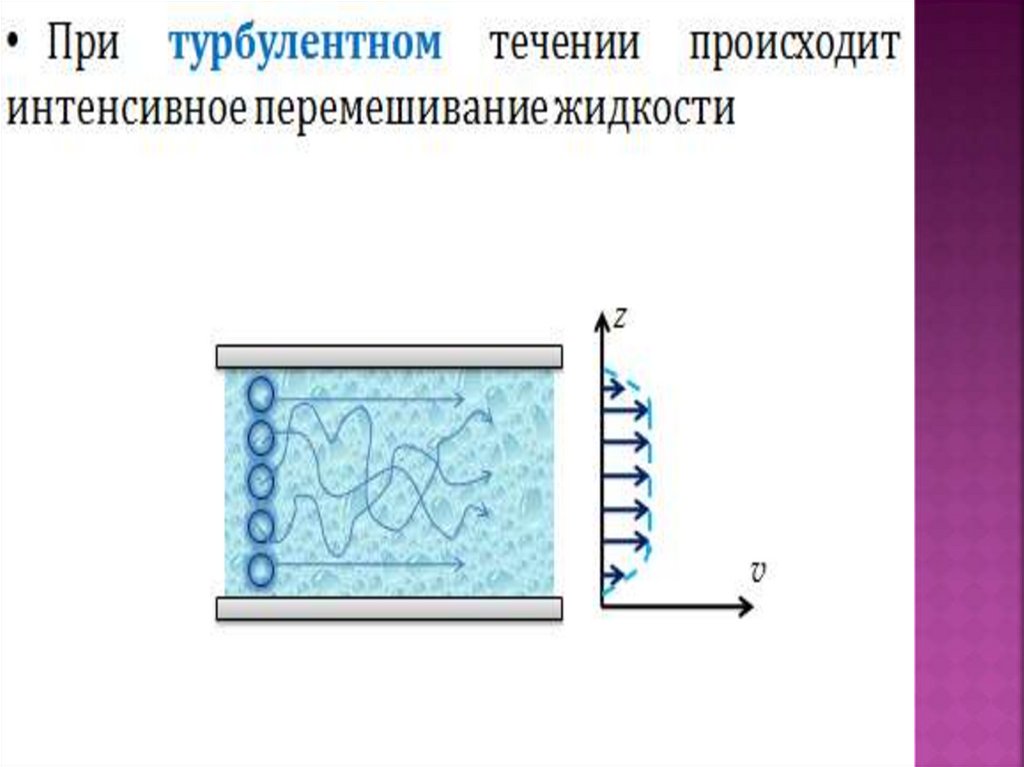
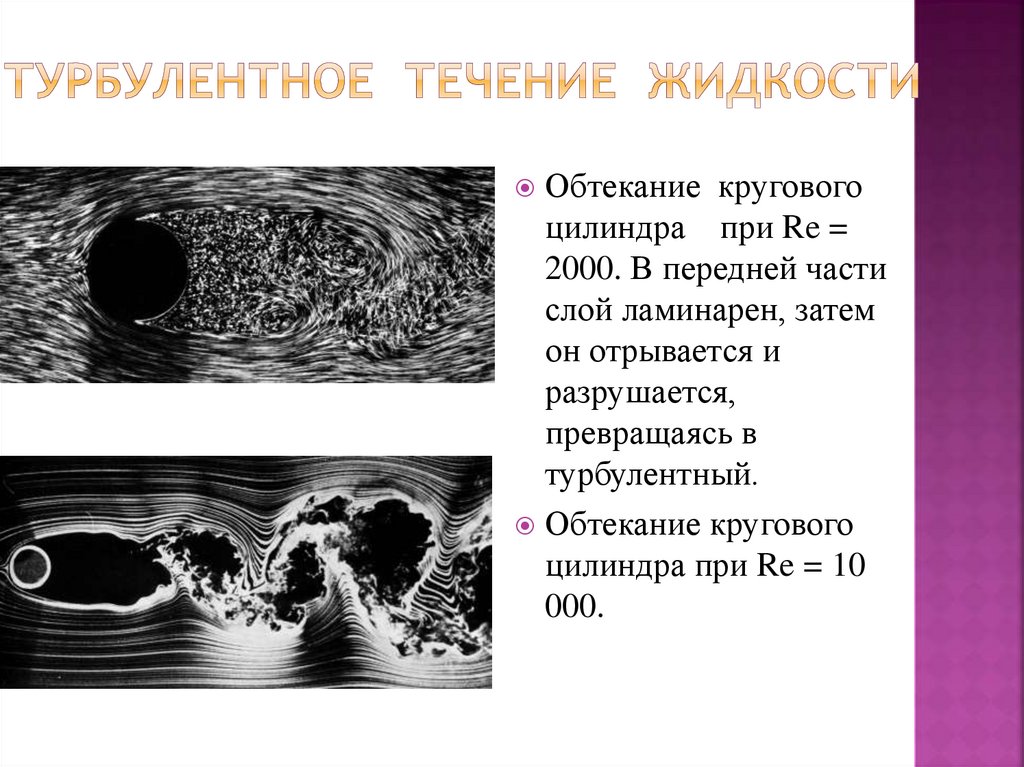
28. Турбулентное течение жидкости

Обтекание кругового
цилиндра при Re =
2000. В передней части
слой ламинарен, затем
он отрывается и
разрушается,
превращаясь в
турбулентный.
Обтекание кругового
цилиндра при Re = 10
000.

29.

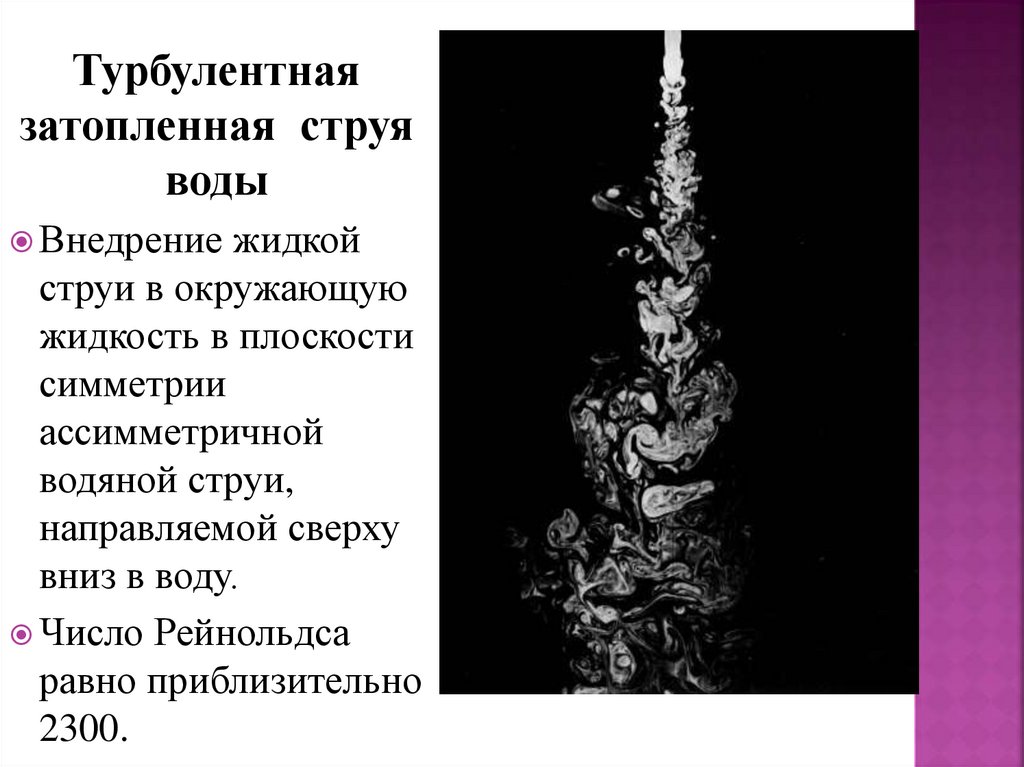
Турбулентная
затопленная струя
воды
Внедрение жидкой
струи в окружающую
жидкость в плоскости
симметрии
ассимметричной
водяной струи,
направляемой сверху
вниз в воду.
Число Рейнольдса
равно приблизительно
2300.

30.

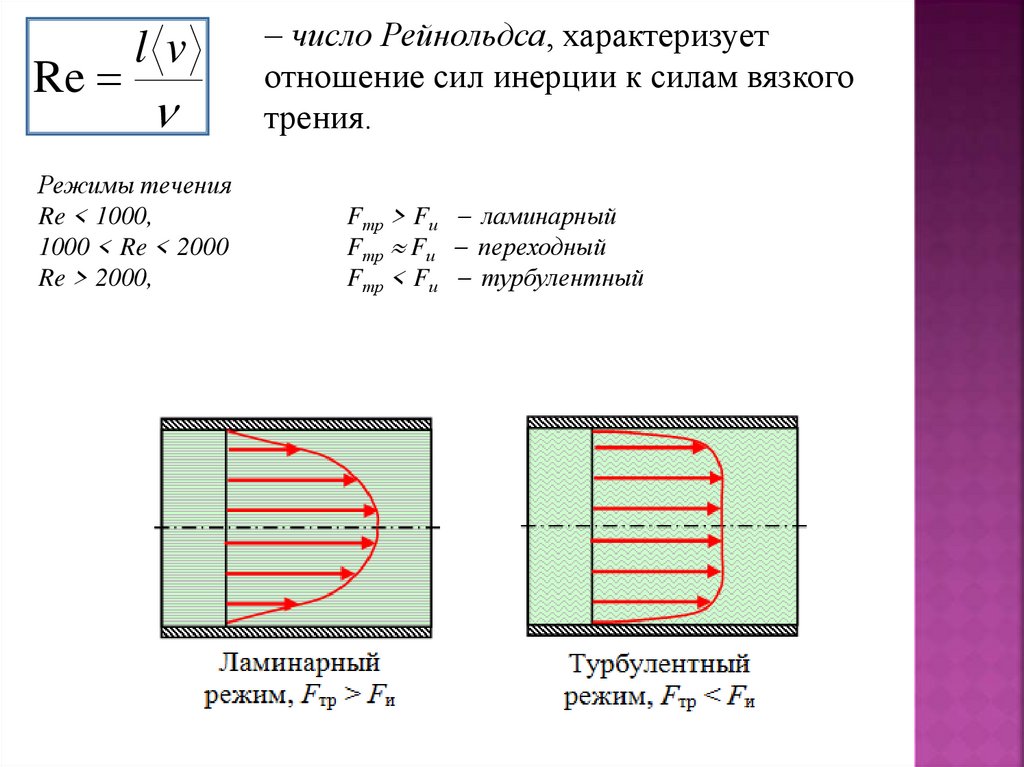
Re
lv
Режимы течения
Re < 1000,
1000 < Re < 2000
Re > 2000,
число Рейнольдса, характеризует
отношение сил инерции к силам вязкого
трения.
Fтр > Fи ламинарный
Fтр Fи переходный
Fтр < Fи турбулентный

31.

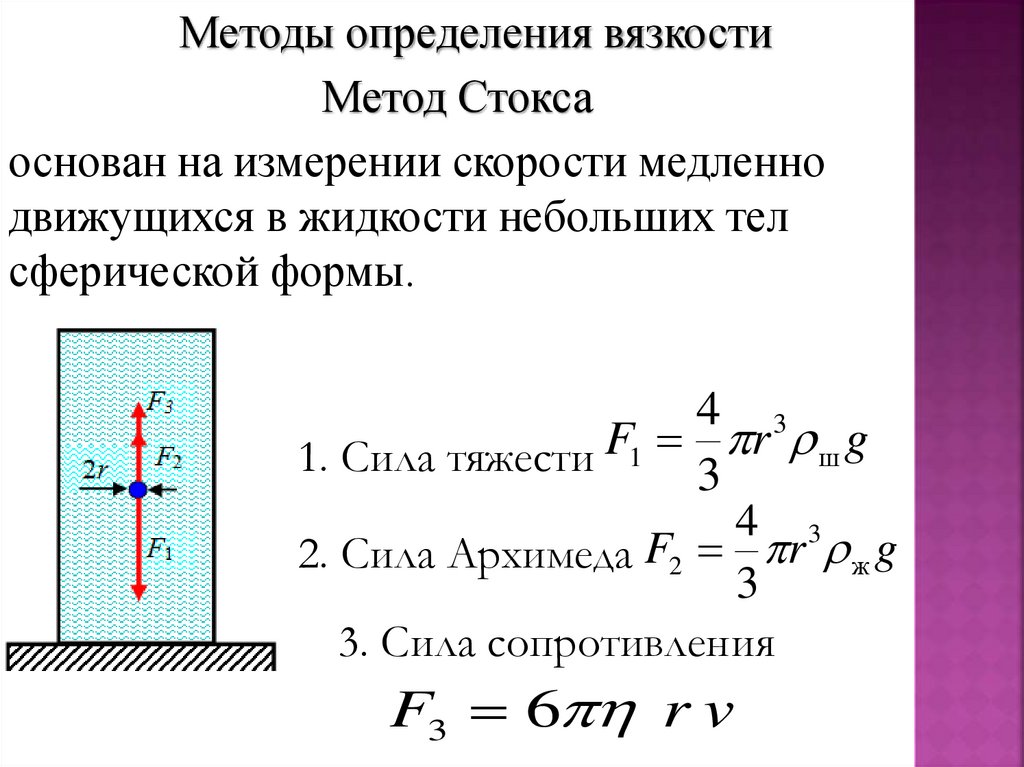
Методы определения вязкости
Метод Стокса
основан на измерении скорости медленно
движущихся в жидкости небольших тел
сферической формы.
4 3
1. Сила тяжести F1 3 r ш g
4 3
2. Сила Архимеда F2 r ж g
3
3. Сила сопротивления
F3 6 r v

32.

При равномерном движении
F1 F2 F3
4 3
4 3
r ш g r ж g 6 r v
3
3
2 ш ρ ж g r
9v
2

33.

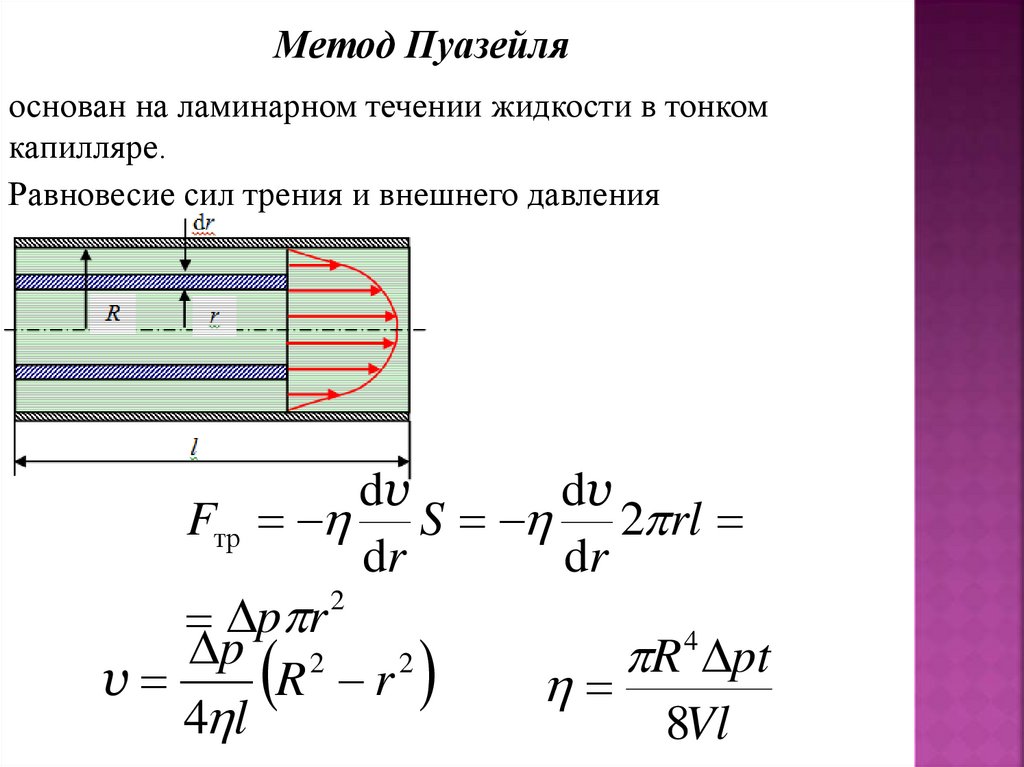
Метод Пуазейля
основан на ламинарном течении жидкости в тонком
капилляре.
Равновесие сил трения и внешнего давления
dv
dv
Fтр S 2 rl
dr
dr
2
p
r
4
p 2 2
R
pt
v
R r
4 l
8Vl