Л1_Аксиомы стереометрии. Доказательство первых теорем стереометрии

1.

Лекция 1
Аксиомы стереометрии.
Доказательство первых
теорем стереометрии

2.

§1 Суть аксиоматического метода
Выделяются начальные
(неопределяемые) объекты и отношения
Формулируется система аксиом,
т.е. утверждений, принимаемых в качестве
исходных (без доказательства).
Они косвенно описывают начальные
объекты и отношения.
Требуется, чтобы все последующие
утверждения были либо теоремами, т.е.
доказывались бы на основании системы
аксиом, либо были определениями.

3.

§1Суть аксиоматического метода
При этом:
При доказательстве n-ной теоремы
аргументами являются n-1 ранее доказанные
теоремы и аксиомы.
При доказательстве первой теоремы
аргументами являются аксиомы.
При введении n-ного определения понятия
могут использоваться n-1 ранее вводимых
определений.
При первом определении – только начальные
понятия.

4.

§1Суть аксиоматического метода
• К системе аксиом предъявляются
требования:
непротиворечивости
независимости
полноты

5.

§1Суть аксиоматического метода
Опр. Система аксиом называется
непротиворечивой, если в ней и ее
следствиях не содержится утверждений,
являющихся отрицанием друг друга.
Требование непротиворечивости
является обязательным для любой системы
аксиом, так как противоречивая система не
может служить для построения какой-либо
теории вообще.

6.

§1 Суть аксиоматического метода
• Опр. Система аксиом называется
независимой, если любая ее аксиома не
зависит от остальных аксиом этой системы
(не является следствием).
Требование независимости аксиом не
является столь обязательным, как
требование непротиворечивости. Например,
в школьной геометрии это требование не
выдерживается (из методических
соображений).

7.

§1 Суть аксиоматического метода
• Опр. Система аксиом называется полной,
если любое утверждение,
сформулированное в терминах этой
системы (и ее теории), можно доказать или
опровергнуть.

8.

§2 Эволюция взглядов на основания
геометрии
• Аксиоматический метод явился
инструментом построения теорий
математики и позволил ей превратиться из
эмпирического знания в строгую науку.
• Попытки формально-дедуктивного вывода
ее из собственных первоначальных понятий
и аксиом предпринимались еще в эпоху
становления основ математики (задолго до
Евклида, древние вавилоняне, египтяне и
греки).

9. Замечания

§2 Эволюция взглядов на основания
Замечания
геометрии
Гиппократ
Хиосский
(470-410 гг.
до н.э.)
Платон
(427-347 гг.
до н.э., Афины)
Аристотель
(384-322гг.
до н.э., Стагир)
Евклид
Александрийский
(IV-III вв. до н.э.)

10.

§2 Эволюция взглядов на основания
геометрии
Идея аксиоматического метода Евклида:
• Если мы не можем определить, что
представляет собой исследуемый объект,
то следует определить его свойства,
выделить существенные признаки объекта
и абстрагироваться от несущественных.
• Если эти признаки подобраны хорошо, то
сам объект ими полностью определяется.

11.

«НАЧАЛА» ЕВКЛИДА

12.

§3 Аксиомы стереометрии в
школьном учебнике геометрии
• В геометрии 10 класса Л.А. Латотин и др. (Геометрия
10, 2020г.) предложена следующая аксиоматика
(с.24):
• А1. Если три точки не лежат на одной прямой,
то через них проходит единственная плоскость.

13.

§3 Аксиомы стереометрии в
школьном учебнике геометрии
• В геометрии 10 класса Л.А. Латотин и др. (Геометрия
10, 2020г.) предложена следующая аксиоматика
(с.24):
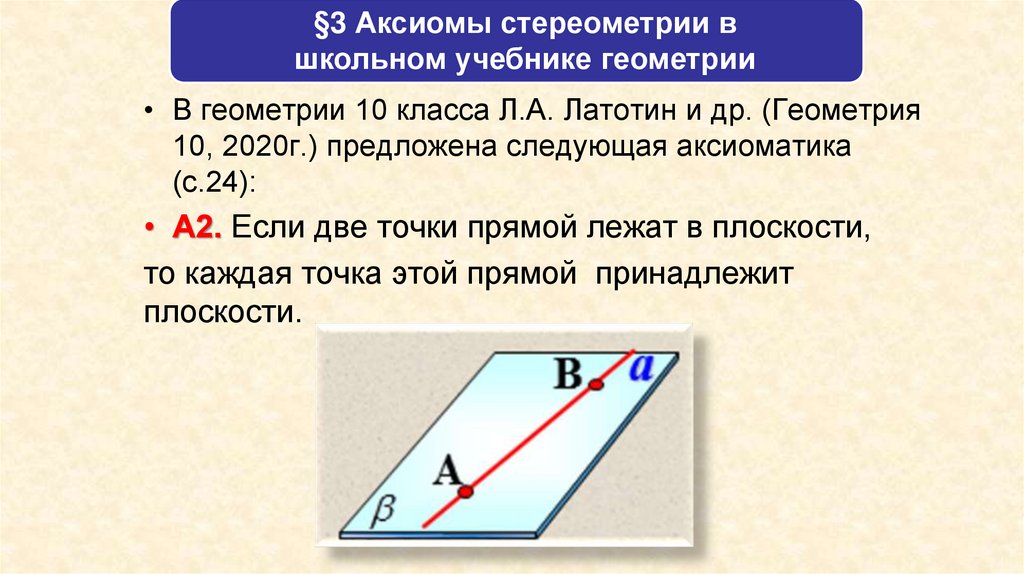
• А2. Если две точки прямой лежат в плоскости,
то каждая точка этой прямой принадлежит
плоскости.

14.

§3 Аксиомы стереометрии в
школьном учебнике геометрии
• В геометрии 10 класса Л.А. Латотин и др. (Геометрия
10, 2020г.) предложена следующая аксиоматика
(с.24):
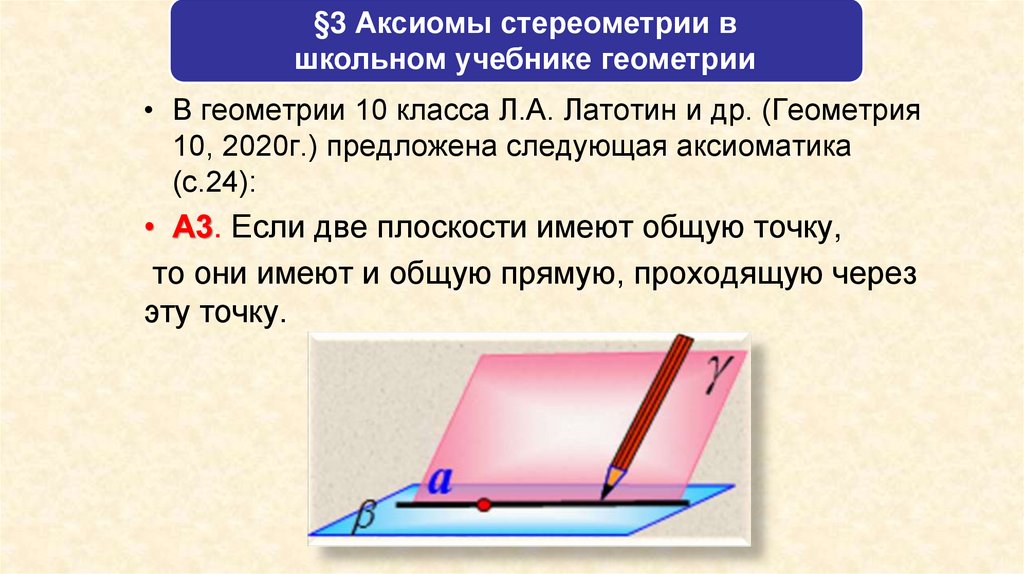
• А3. Если две плоскости имеют общую точку,
то они имеют и общую прямую, проходящую через
эту точку.

15.

§3 Аксиомы стереометрии в
школьном учебнике геометрии
• В геометрии 10 класса Л.А. Латотин и др. (Геометрия
10, 2020г.) предложена следующая аксиоматика
(с.24):
• А1. Если три точки не лежат на одной прямой,
то через них проходит единственная плоскость.
• А2. Если две точки прямой лежат в плоскости,
то каждая точка этой прямой принадлежит
плоскости.
• А3. Если две плоскости имеют общую точку,
то они имеют и общую прямую, проходящую через
эту точку.

16.

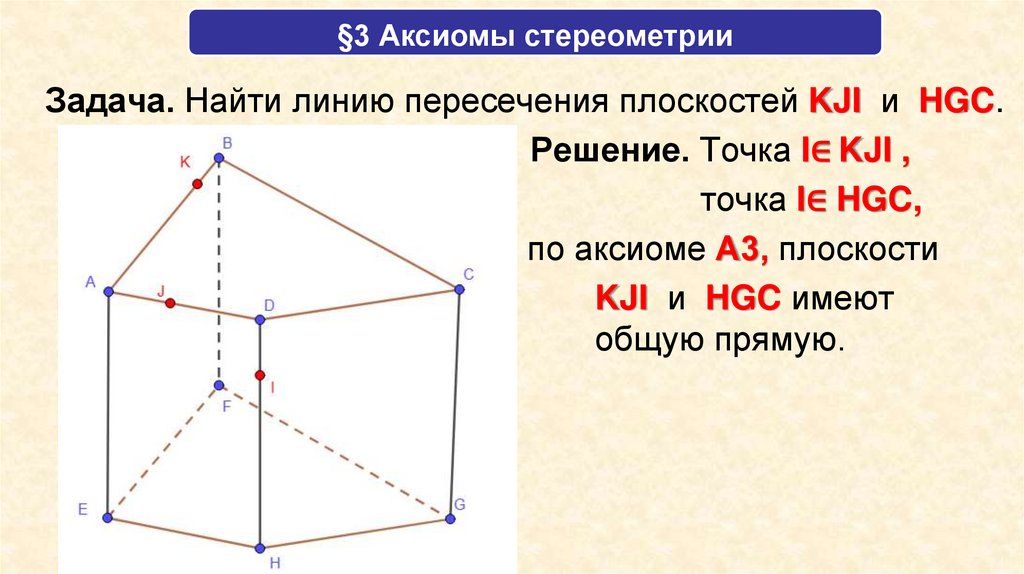
§3 Аксиомы стереометрии
Задача. Найти линию пересечения плоскостей KJI и HGC.
Решение. Точка I∈ KJI ,
точка I∈ HGC,
по аксиоме А3, плоскости
KJI и HGC имеют
общую прямую.

17.

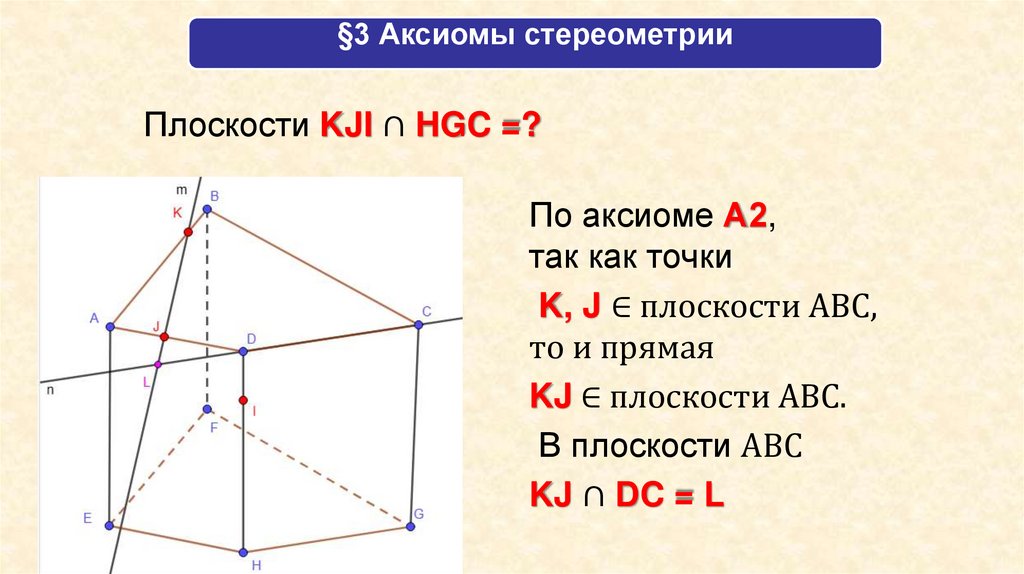
§3 Аксиомы стереометрии
Плоскости KJI ∩ HGC =?
По аксиоме А2,
так как точки
K, J ∈ плоскости АВС,
то и прямая
KJ ∈ плоскости АВС.
В плоскости АВС
KJ ∩ DC = L

18.

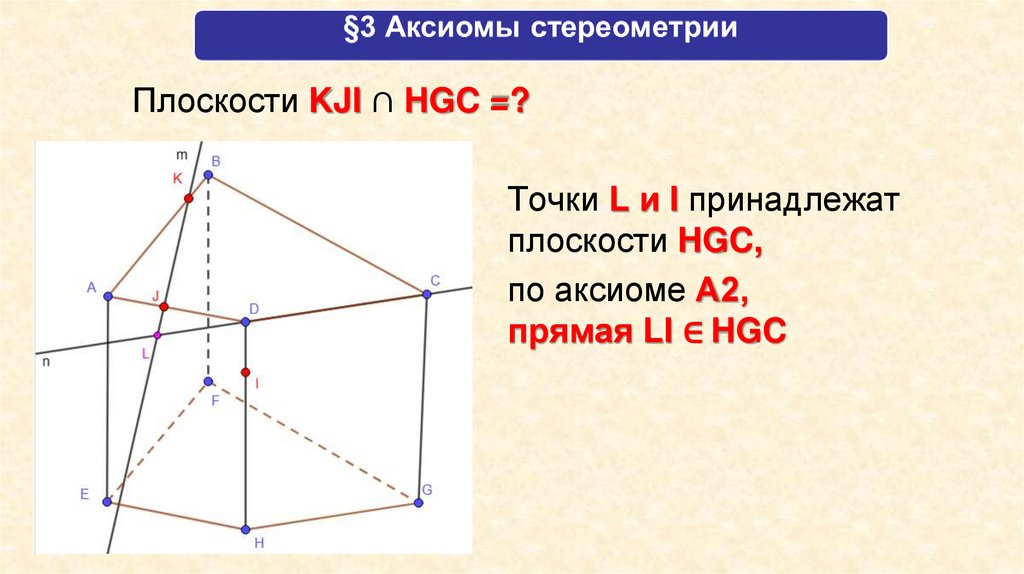
Плоскости KJI ∩ HGC =?
Точки L и I принадлежат
плоскости HGC,
по аксиоме А2,
прямая LI ∈ HGC

19.

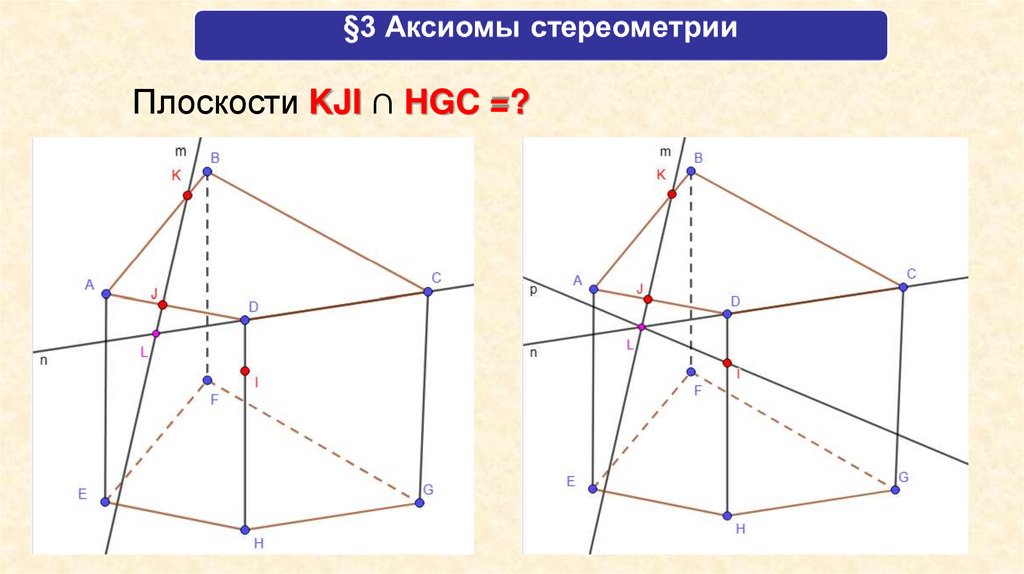
Плоскости KJI ∩ HGC =?

20.

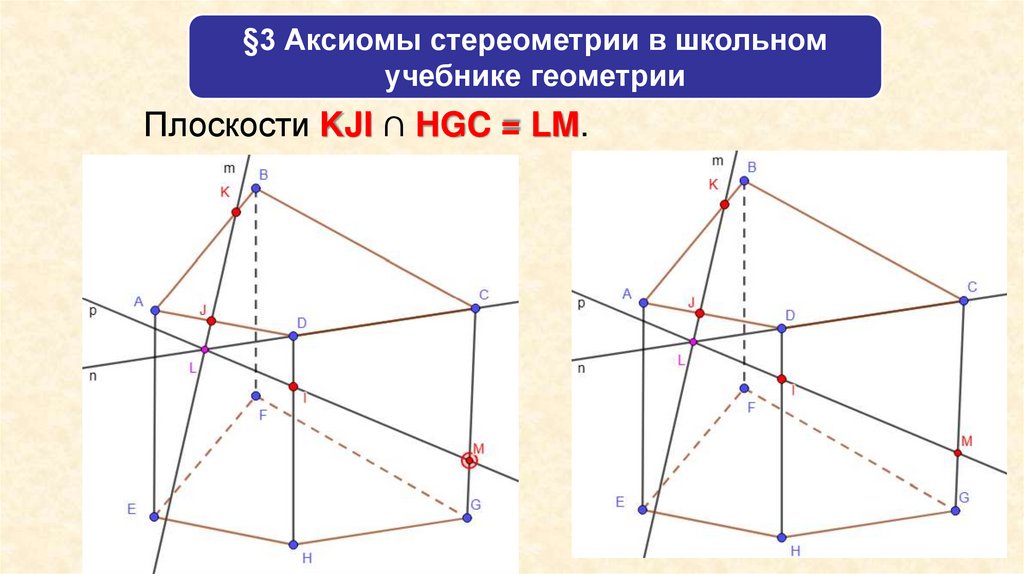
§3 Аксиомы стереометрии в школьном
учебнике геометрии
Плоскости KJI ∩ HGC = LM.

21.

§4 Доказательство первых теорем
стереометрии
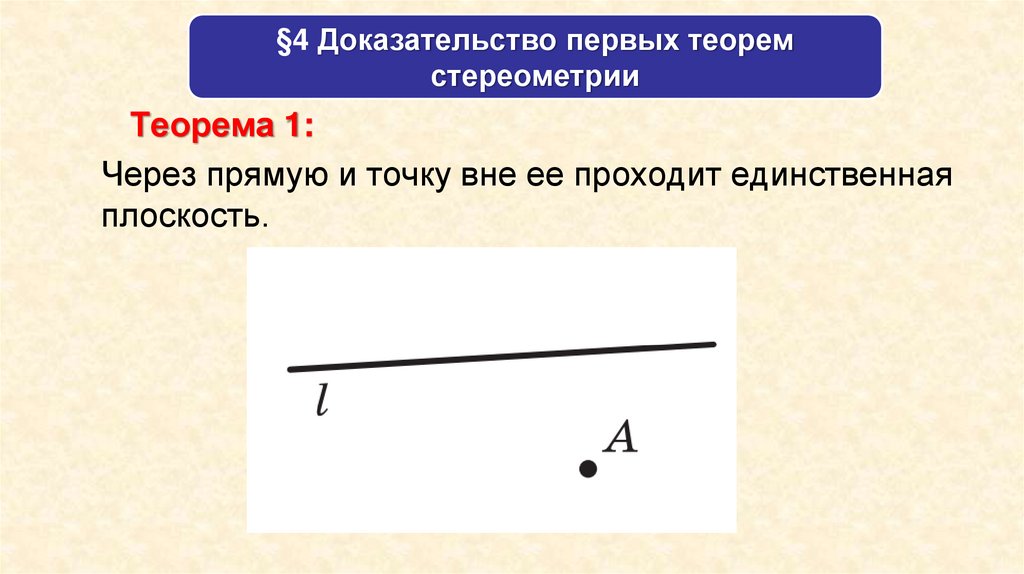
Теорема 1:
Через прямую и точку вне ее проходит единственная
плоскость.

22.

§3 Доказательство первых теорем
стереометрии
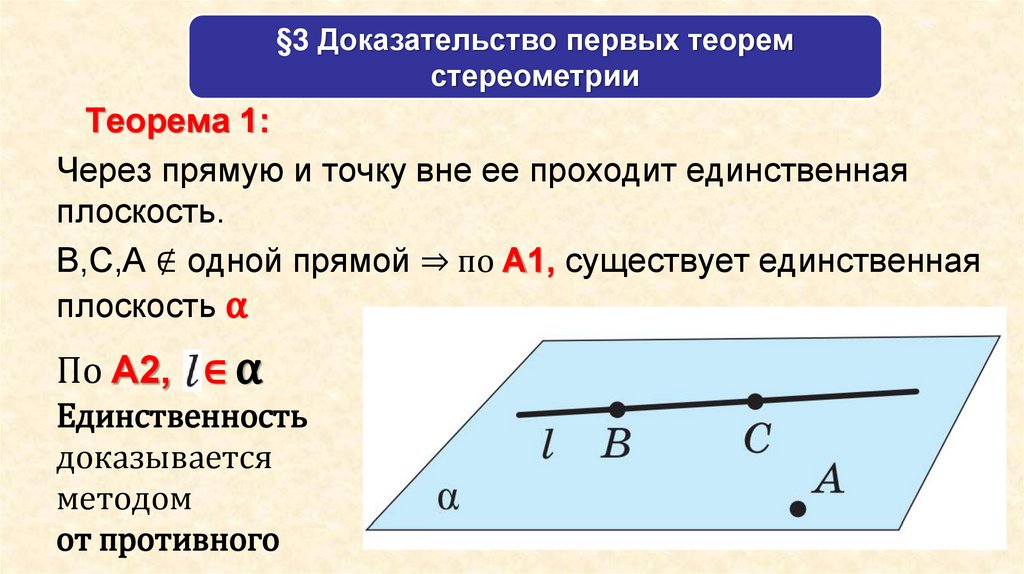
Теорема 1:
Через прямую и точку вне ее проходит единственная
плоскость.
В,С,А ∉ одной прямой ⇒ по А1, существует единственная
плоскость α
По А2, ∈ α
Единственность
доказывается
методом
от противного

23.

§3 Доказательство первых теорем
стереометрии
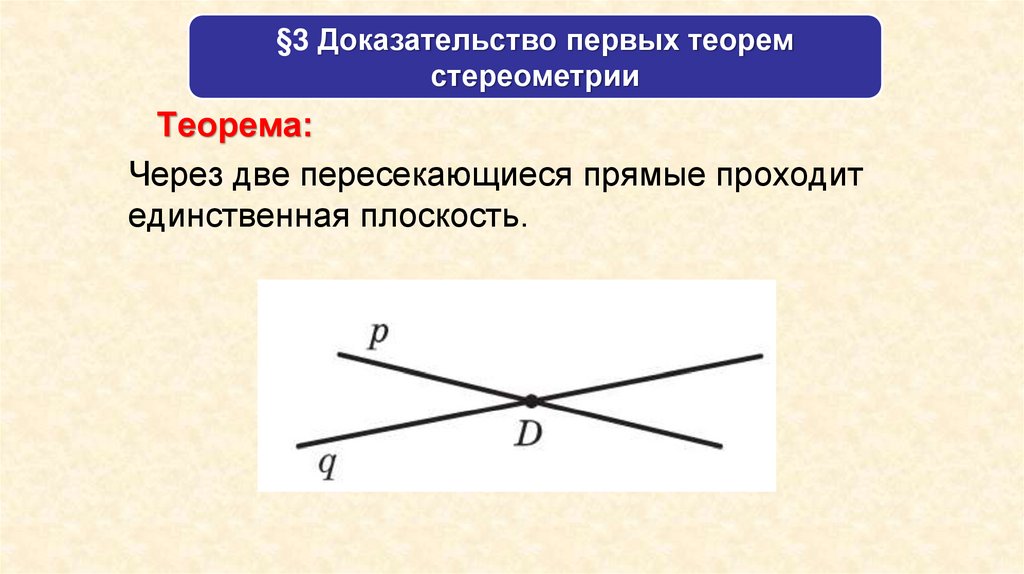
Теорема:
Через две пересекающиеся прямые проходит
единственная плоскость.

24.

§4 Доказательство первых теорем
стереометрии
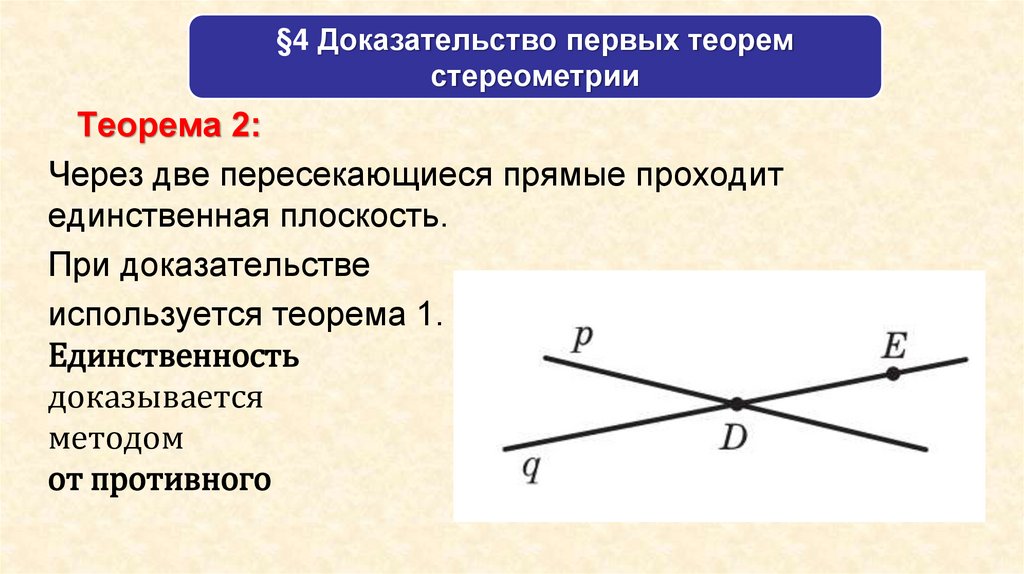
Теорема 2:
Через две пересекающиеся прямые проходит
единственная плоскость.
При доказательстве
используется теорема 1.
Единственность
доказывается
методом
от противного

25.

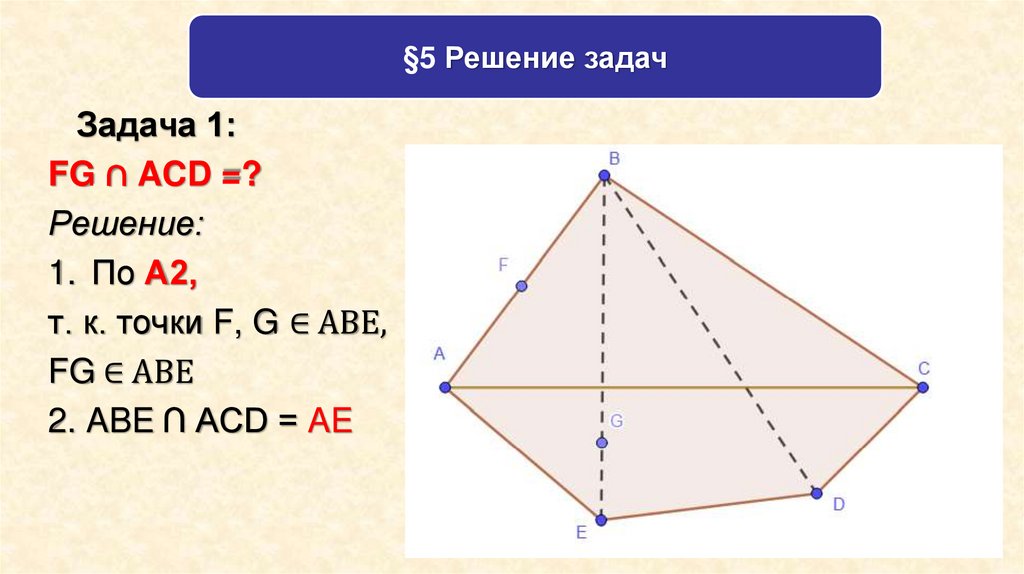
§5 Решение задач
Задача 1:
FG ∩ ACD =?
Решение:
1. По А2,
т. к. точки F, G ∈ ABE,
FG ∈ ABE
2. ABE ∩ ACD = AE

26.

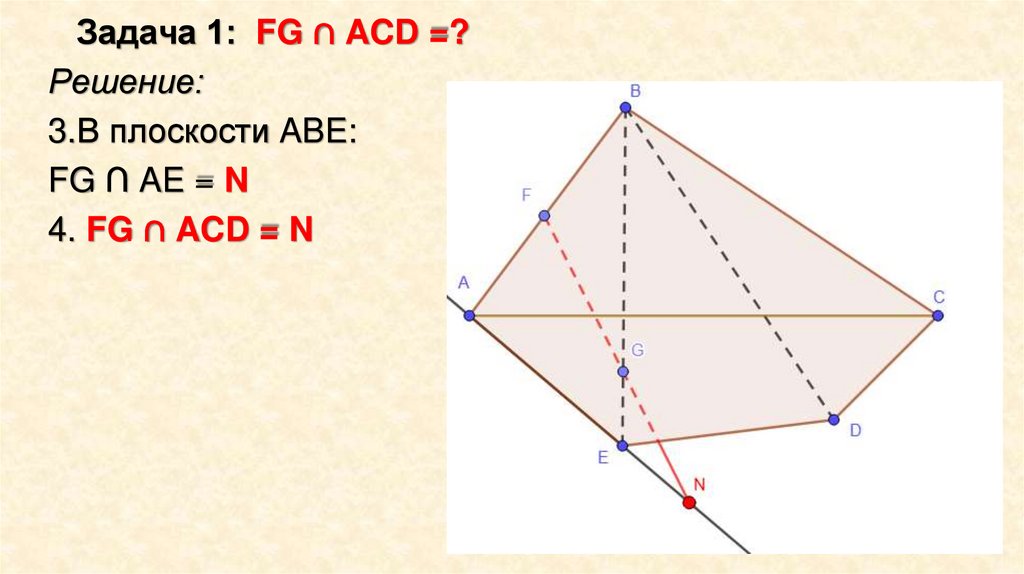
Задача 1: FG ∩ ACD =?
Решение:
3.В плоскости ABE:
FG ∩ AE = N
4. FG ∩ ACD = N

27.

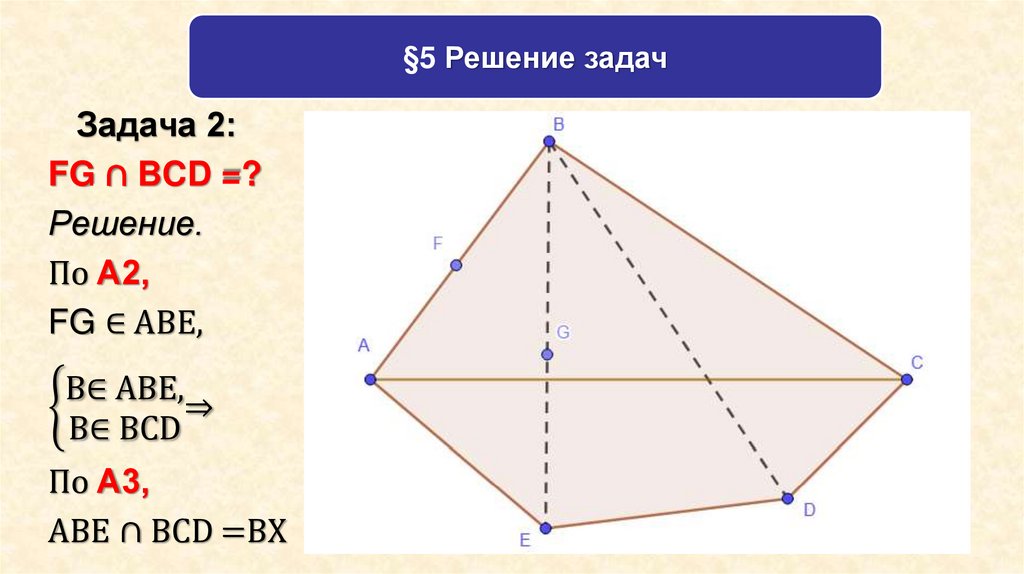
§5 Решение задач
Задача 2:
FG ∩ BCD =?
Решение.
По А2,
FG ∈ ABE,
B∈ ABE,
ቊ
⇒
B∈ BCD
По А3,
ABE ∩ BCD =ВХ

28.

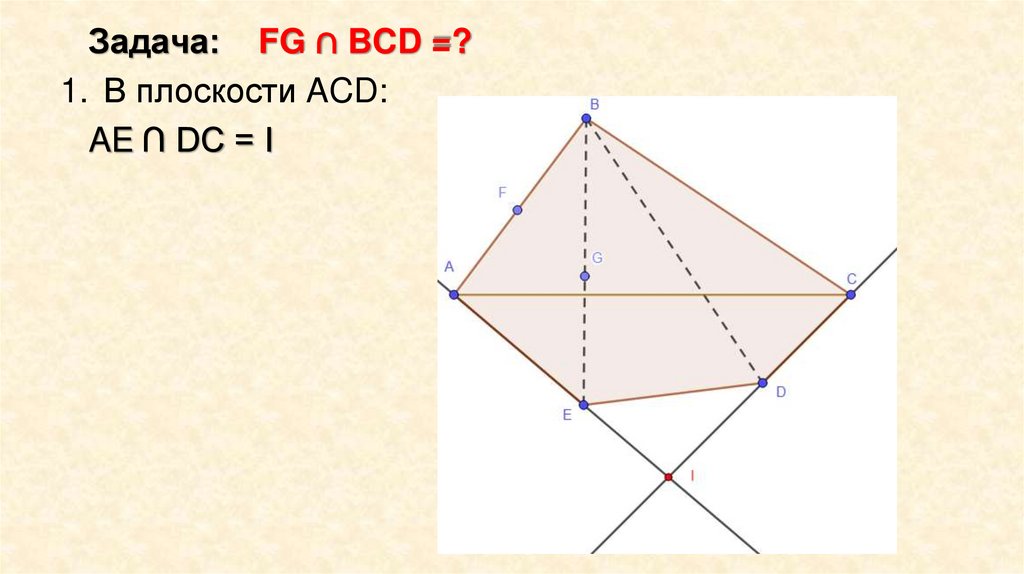
Задача: FG ∩ BCD =?
1. В плоскости ACD:
AE ∩ DC = I

29.

Задача: FG ∩ BCD =?
Решение.
1. AE ∩ DC = I
2. ABE ∩ BDC = IB

30.

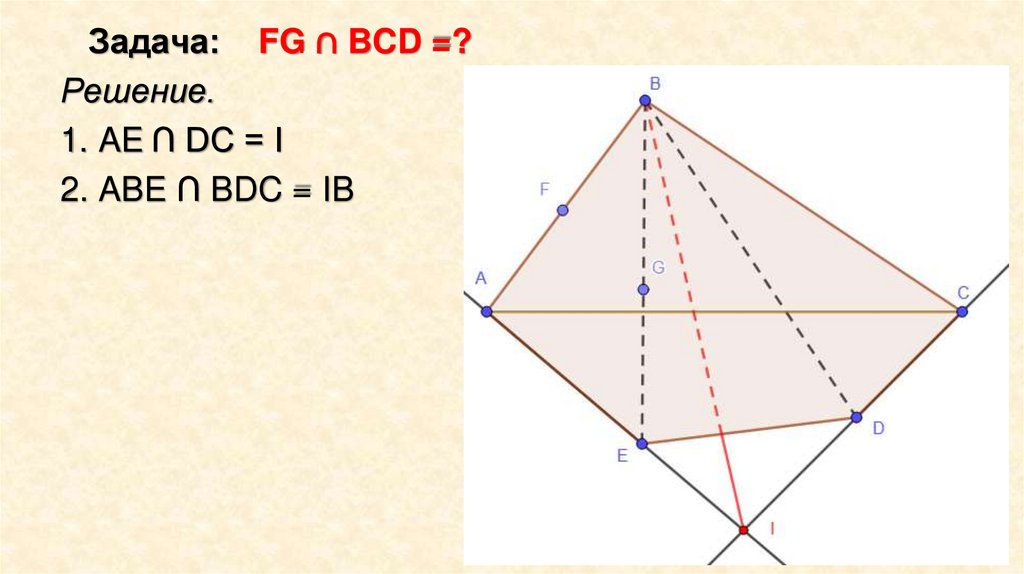
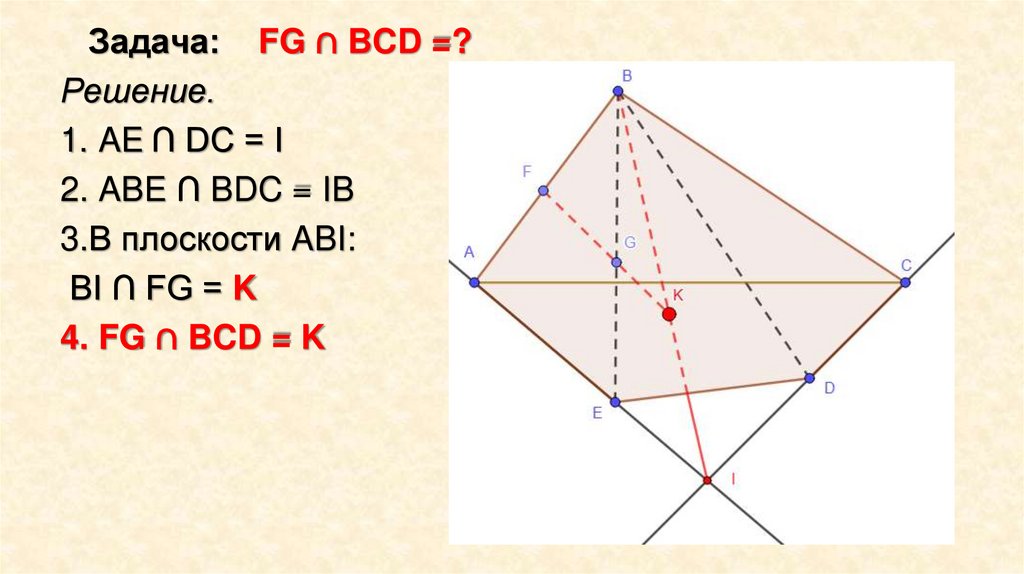
Задача: FG ∩ BCD =?
Решение.
1. AE ∩ DC = I
2. ABE ∩ BDC = IB
3.В плоскости ABI:
BI ∩ FG = K
4. FG ∩ BCD = K