Similar presentations:
Предмет стереометрии
1. Предмет стереометрии
http://linda6035.ucoz.ru/2. Геометрия (греч.)
наука о свойствахгеометрических фигур
гео –земля
метрео - измерять
http://linda6035.ucoz.ru/
3. Геометрия
Планиметрияот лат. planum —
плоскость и... метрия
Стереометрия
от др.-греч. στερεός, «стереос» —
«пространственный,объемный»
http://linda6035.ucoz.ru/
4. Геометрия
Планиметрияhttp://linda6035.ucoz.ru/
Стереометрия
5.
раздел геометрии, в котором изучаютсясвойства тел в пространстве
http://linda6035.ucoz.ru/
6.
Евклид — жил около 300 г. до н. э,первый математик Александрийской школы.
Его главная работа «Начала» содержит
изложение планиметрии, стереометрии.
Его называют «отцом геометрии».
Дави́д Ги́льберт (1862-1943) —
немецкий математик-универсал,
внёс значительный вклад в развитие многих
областей математики.
Разработал
аксиоматику
евклидовой
геометрии.
http://linda6035.ucoz.ru/
7.
Основные фигуры в пространстветочка
плоскость
прямая
http://linda6035.ucoz.ru/
8.
A, B, C, …A
B
a, b, c, …
или
или
http://linda6035.ucoz.ru/
AВ, BС, CD, …
b
C
, , ,...
ABC ,...
C
D
9.
Основные фигуры в пространстве⍺
М
точка
плоскость
прямая
http://linda6035.ucoz.ru/
а
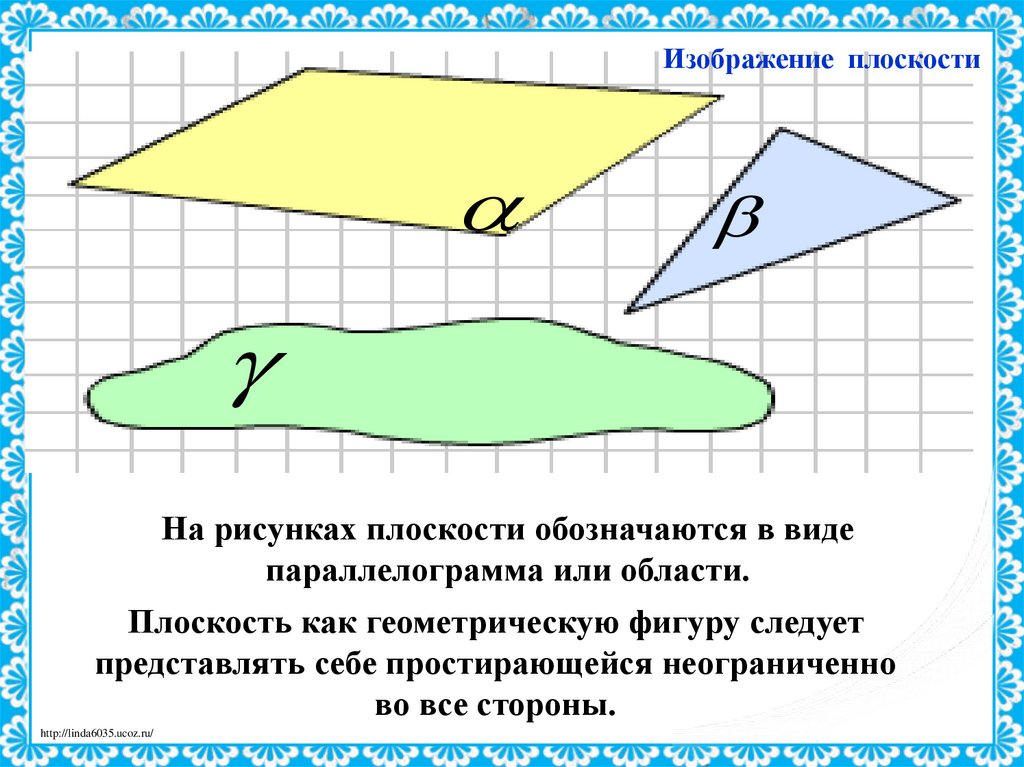
10. Изображение плоскости
На рисунках плоскости обозначаются в видепараллелограмма или области.
Плоскость как геометрическую фигуру следует
представлять себе простирающейся неограниченно
во все стороны.
http://linda6035.ucoz.ru/
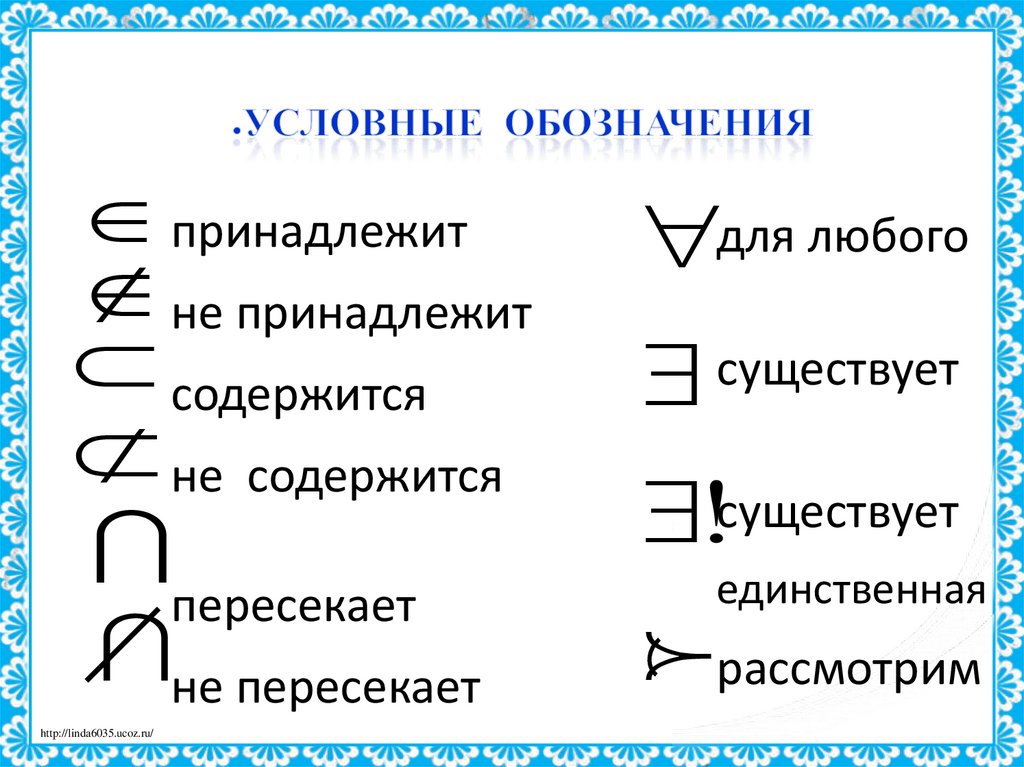
11. Условные обозначения
принадлежитне принадлежит
содержится
не содержится
пересекает
не пересекает
http://linda6035.ucoz.ru/
для любого
существует
!существует
единственная
рассмотрим
12. Что такое аксиома?
АКСИОМА (axíõma - греческое слово,означающее «бесспорное положение») –
это высказывание, истинность которого
принимается без доказательства .
Аксиомы были сформулированы Евклидом
( III в. до н. э.) в его знаменитом сочинении
«Начала».
На основе аксиом доказываются теоремы и
строится вся геометрия
http://linda6035.ucoz.ru/
13.
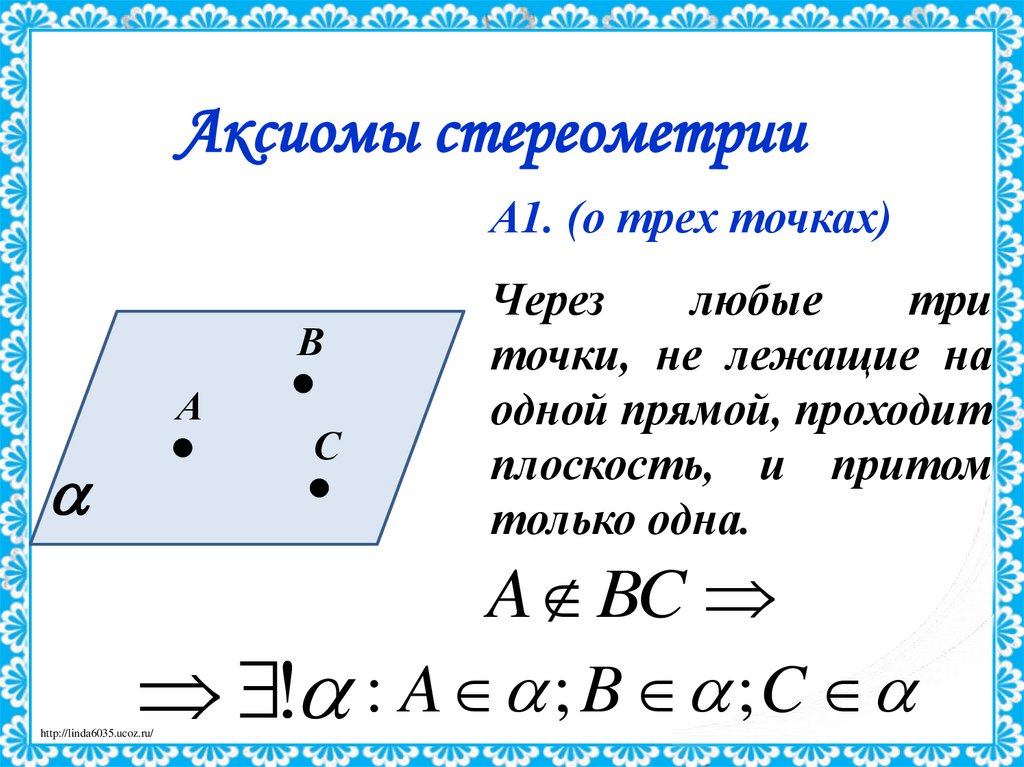
Аксиомы стереометрииА1. (о трех точках)
В
А
С
Через
любые
три
точки, не лежащие на
одной прямой, проходит
плоскость, и притом
только одна.
A BC
! : A ; B ; C
http://linda6035.ucoz.ru/
14.
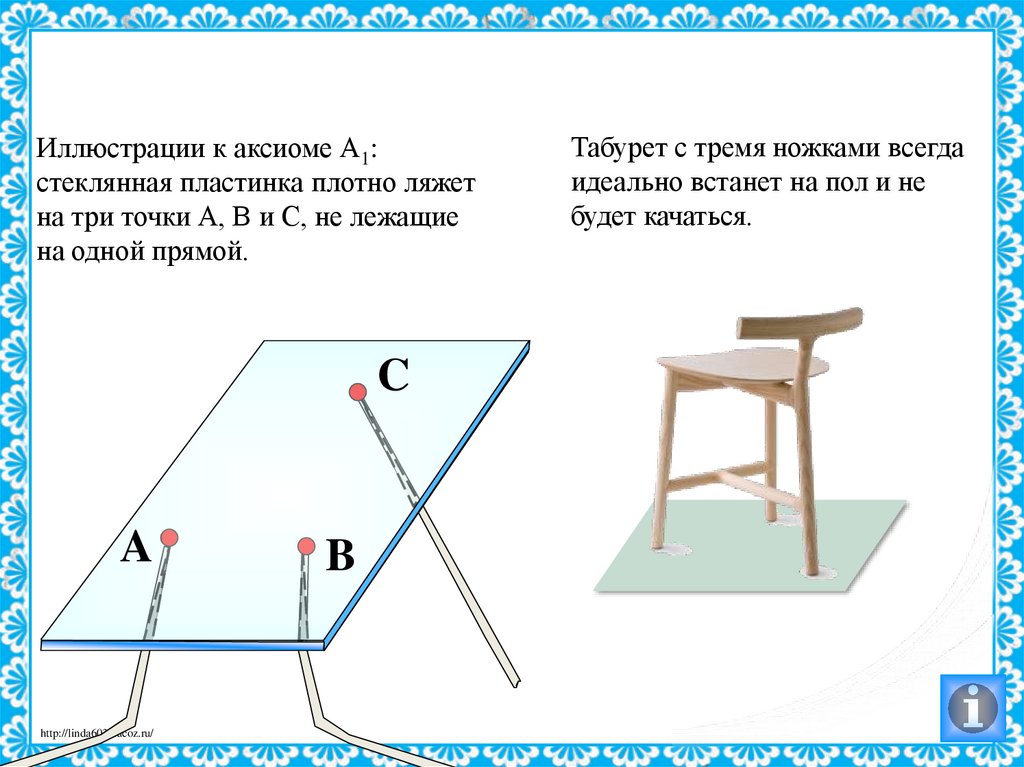
Иллюстрации к аксиоме А1:стеклянная пластинка плотно ляжет
на три точки А, В и С, не лежащие
на одной прямой.
C
A
http://linda6035.ucoz.ru/
B
Табурет с тремя ножками всегда
идеально встанет на пол и не
будет качаться.
15.
Для видеокамеры, фотосъемки и для других приборов частоиспользуют штатив – треногу. Три ножки штатива устойчиво
расположатся на любом полу в помещениях, на асфальте или
прямо на газоне на улице, на песке на пляже или в траве в
лесу. Три ножки штатива всегда найдут плоскость.
http://linda6035.ucoz.ru/
16.
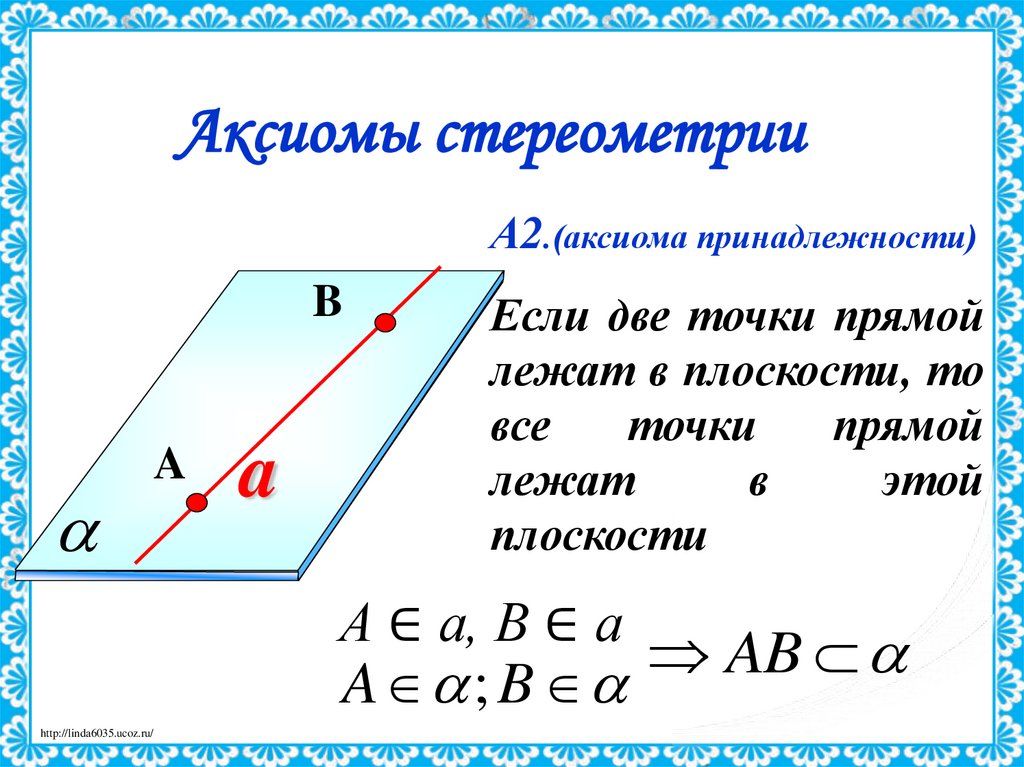
Аксиомы стереометрииА2.(аксиома принадлежности)
Если две точки прямой
лежат в плоскости, то
все
точки
прямой
лежат
в
этой
плоскости
http://linda6035.ucoz.ru/
17.
Аксиомы стереометрииА2.(аксиома принадлежности)
B
A
a
Если две точки прямой
лежат в плоскости, то
все
точки
прямой
лежат
в
этой
плоскости
А ∈ а, В ∈ а
AB
A ; B
http://linda6035.ucoz.ru/
18.
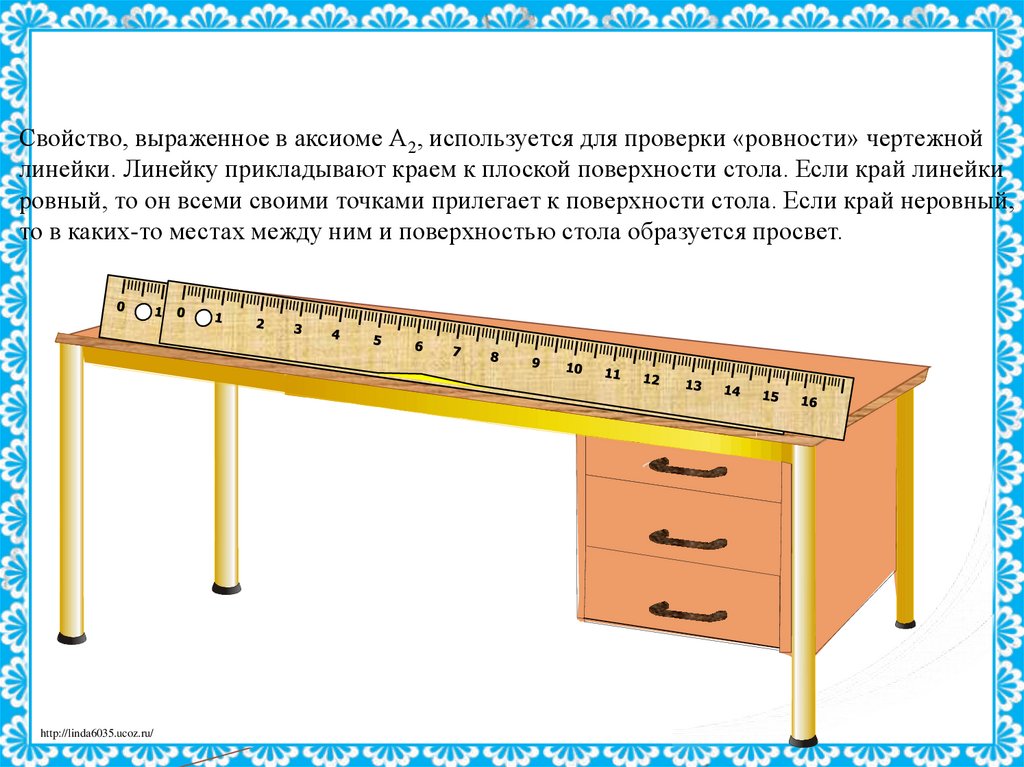
Свойство, выраженное в аксиоме А2, используется для проверки «ровности» чертежнойлинейки. Линейку прикладывают краем к плоской поверхности стола. Если край линейки
ровный, то он всеми своими точками прилегает к поверхности стола. Если край неровный,
то в каких-то местах между ним и поверхностью стола образуется просвет.
http://linda6035.ucoz.ru/
19.
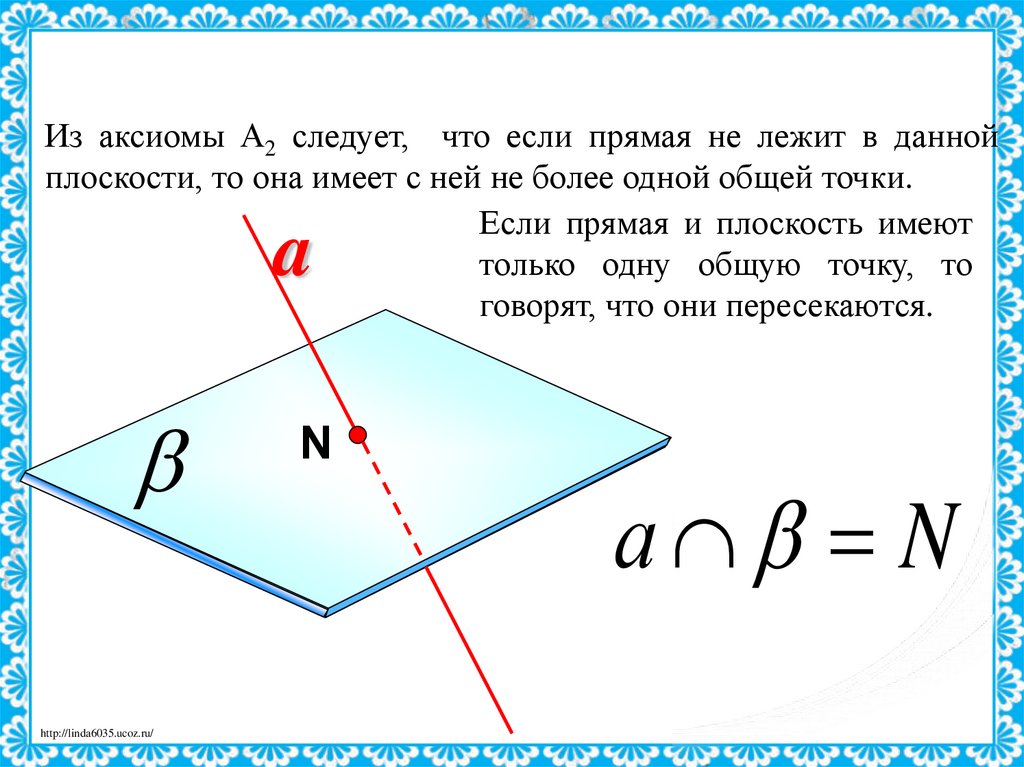
Из аксиомы А2 следует, что если прямая не лежит в даннойплоскости, то она имеет с ней не более одной общей точки.
Если прямая и плоскость имеют
только одну общую точку, то
говорят, что они пересекаются.
a
http://linda6035.ucoz.ru/
N
а N
20.
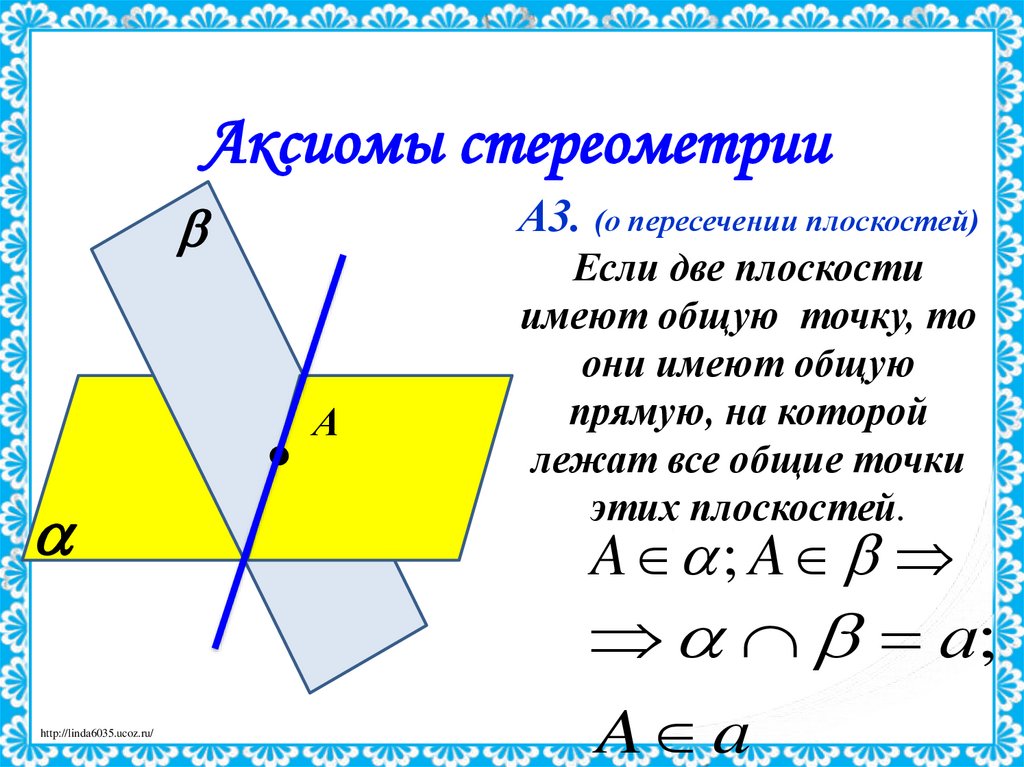
Аксиомы стереометрииА3. (о пересечении плоскостей)
А
http://linda6035.ucoz.ru/
Если две плоскости
имеют общую точку, то
они имеют общую
прямую, на которой
лежат все общие точки
этих плоскостей.
A ; A
а;
A a
21.
http://linda6035.ucoz.ru/Наглядной иллюстрацией аксиомы А3
является пересечение двух смежных стен,
стены и потолка классной комнаты.
22.
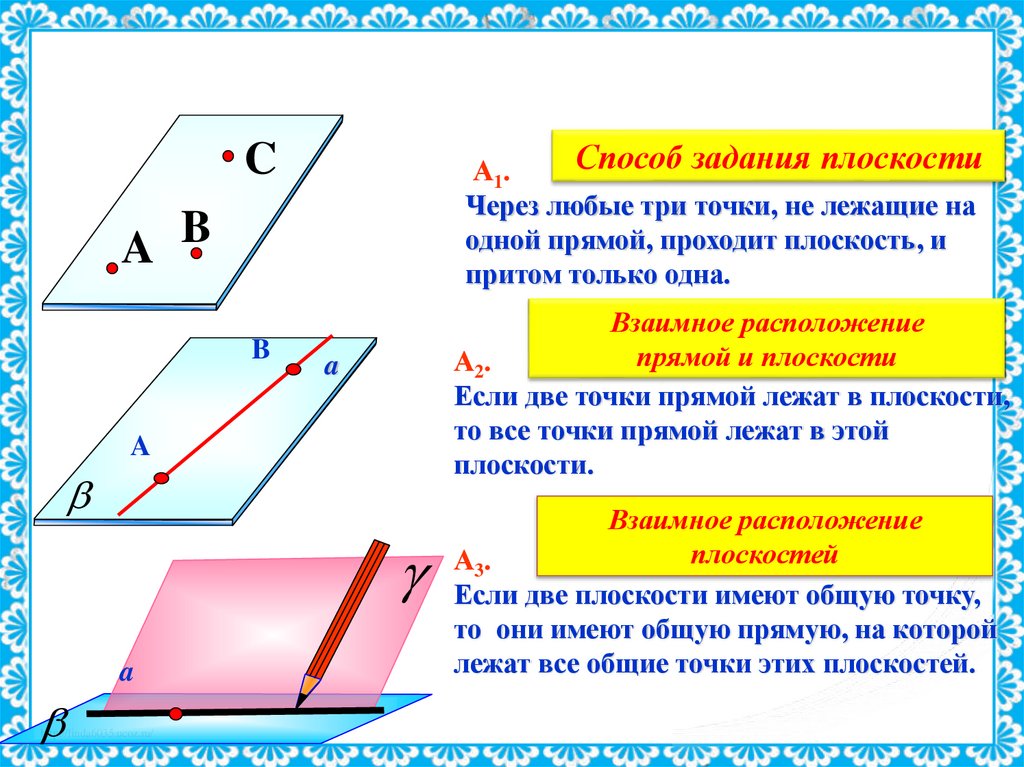
Способ задания плоскостиА1.
Через любые три точки, не лежащие на
одной прямой, проходит плоскость, и
притом только одна.
C
B
A
B
Взаимное расположение
прямой и плоскости
А2.
Если две точки прямой лежат в плоскости,
то все точки прямой лежат в этой
плоскости.
a
A
a
http://linda6035.ucoz.ru/
Взаимное расположение
плоскостей
А3 .
Если две плоскости имеют общую точку,
то они имеют общую прямую, на которой
лежат все общие точки этих плоскостей.
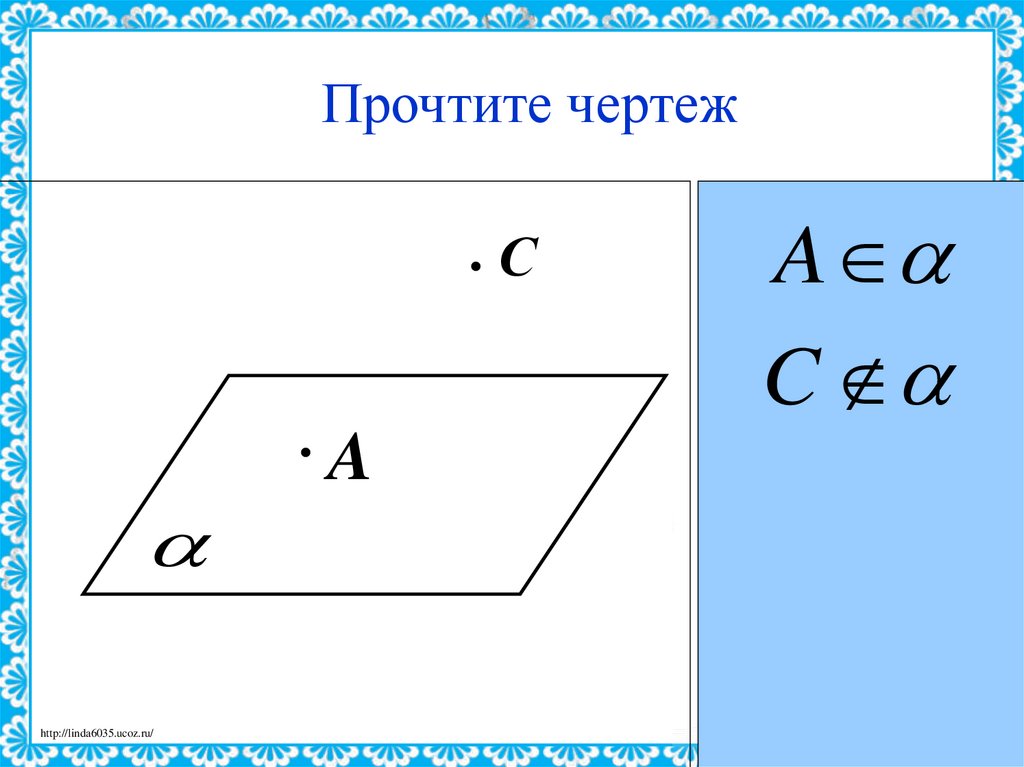
23. Прочтите чертеж
Сhttp://linda6035.ucoz.ru/
A
A
C
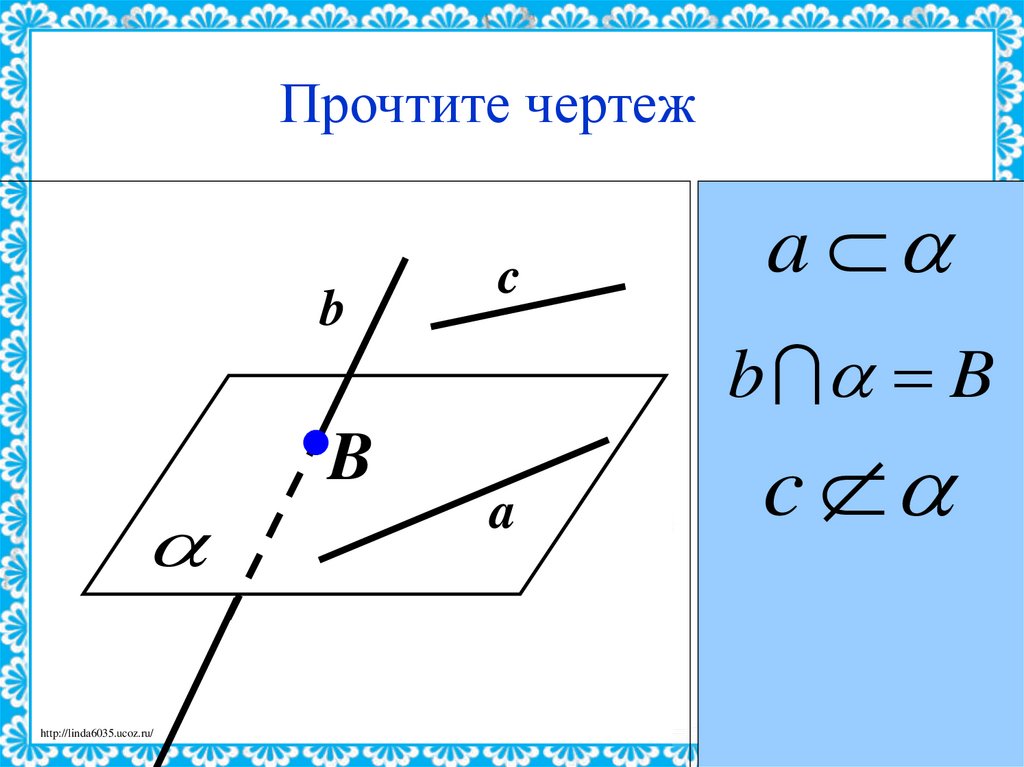
24.
Прочтите чертежb
http://linda6035.ucoz.ru/
B
c
a
b B
a
c
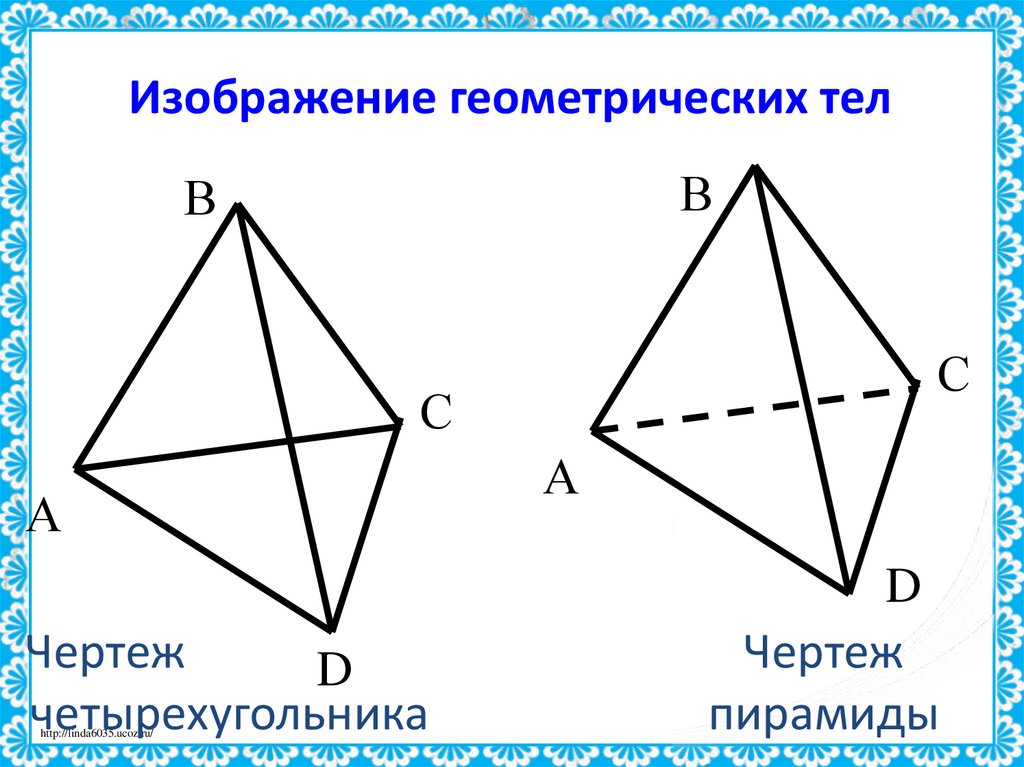
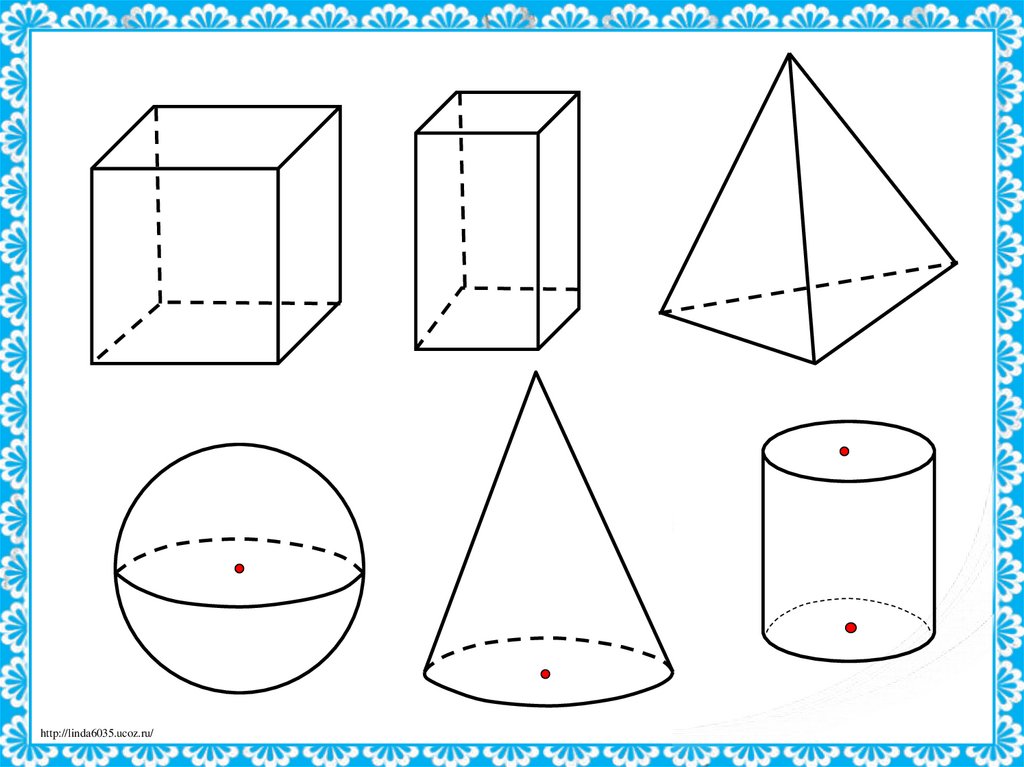
25. Изображение геометрических тел
ВВ
С
С
А
Чертеж
D
четырехугольника
http://linda6035.ucoz.ru/
А
D
Чертеж
пирамиды
26.
http://linda6035.ucoz.ru/27.
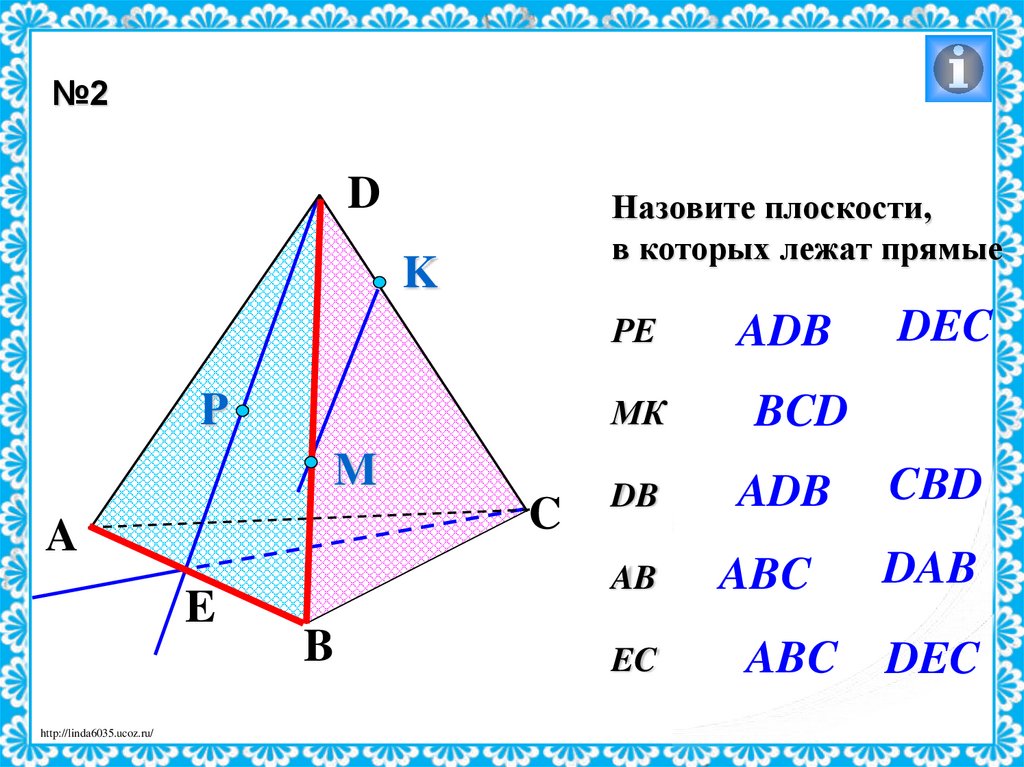
№2D
Назовите плоскости,
в которых лежат прямые
K
P
M
C
A
E
http://linda6035.ucoz.ru/
B
DEC
РЕ
ADB
МК
BCD
DB
ADB
CBD
AB
ABC
DAB
ABC
DEC
EC
28.
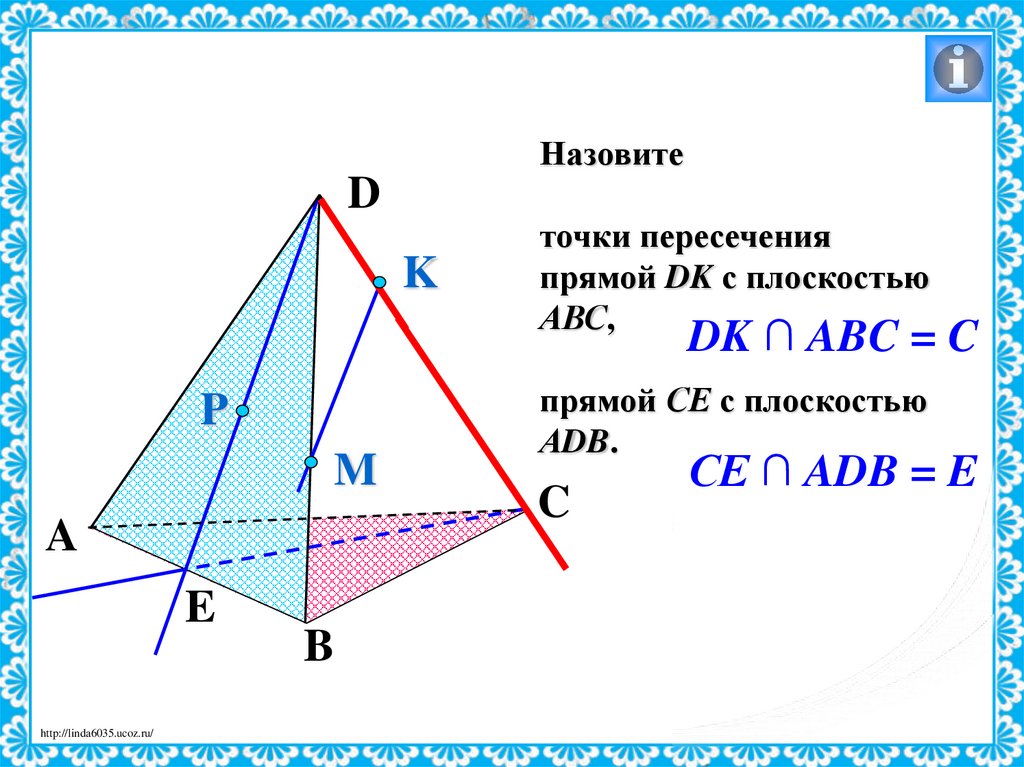
НазовитеD
K
точки пересечения
прямой DK с плоскостью
АВС,
DK ∩ ABC = C
P
M
A
E
http://linda6035.ucoz.ru/
B
прямой СЕ с плоскостью
АDB.
C
СЕ ∩ ADB = E
29.
DK
P
M
A
E
http://linda6035.ucoz.ru/
B
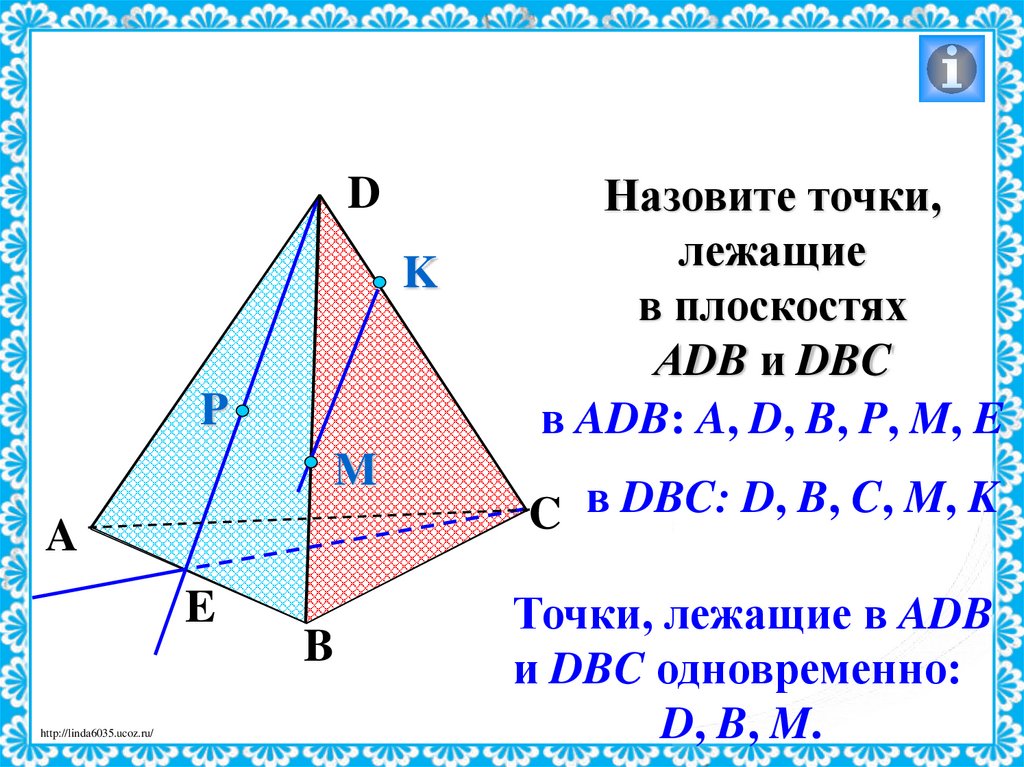
Назовите точки,
лежащие
в плоскостях
АDB и DBC
в ADB: A, D, B, P, M, E
C в DBC: D, B, C, M, K
Точки, лежащие в ADB
и DBC одновременно:
D, B, M.
30.
DK
P
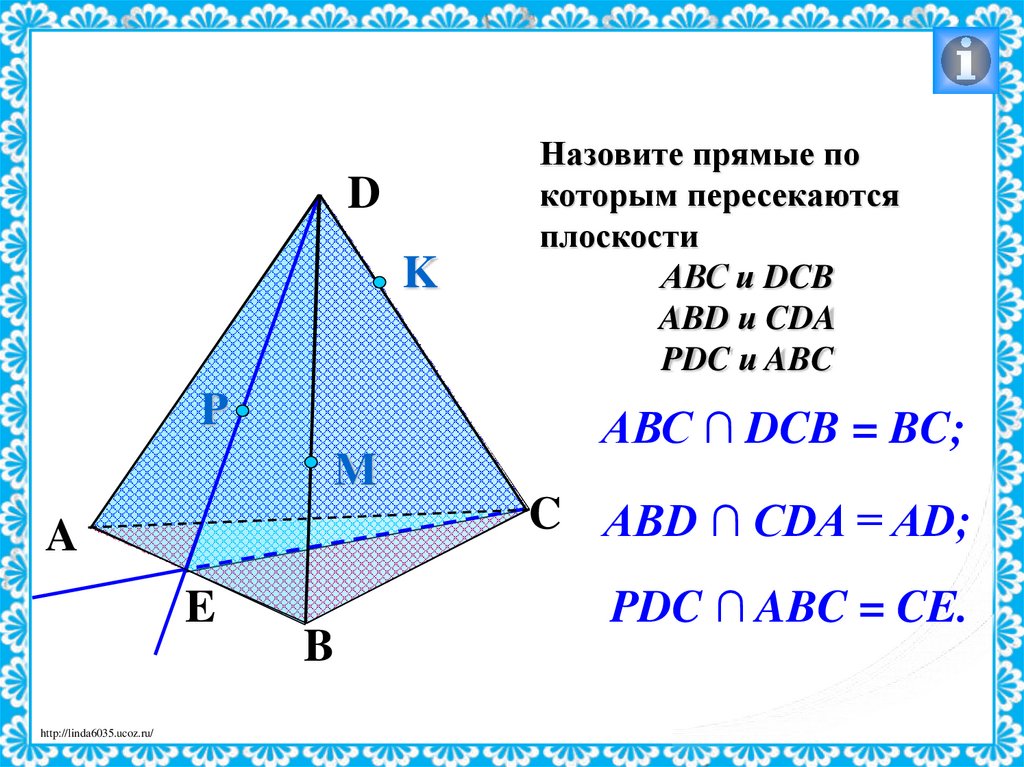
Назовите прямые по
которым пересекаются
плоскости
АВС и DCB
ABD и CDA
PDC и ABC
АВС ∩ DCB = BC;
M
C ABD ∩ CDA = AD;
A
E
http://linda6035.ucoz.ru/
B
PDC ∩ ABC = CE.
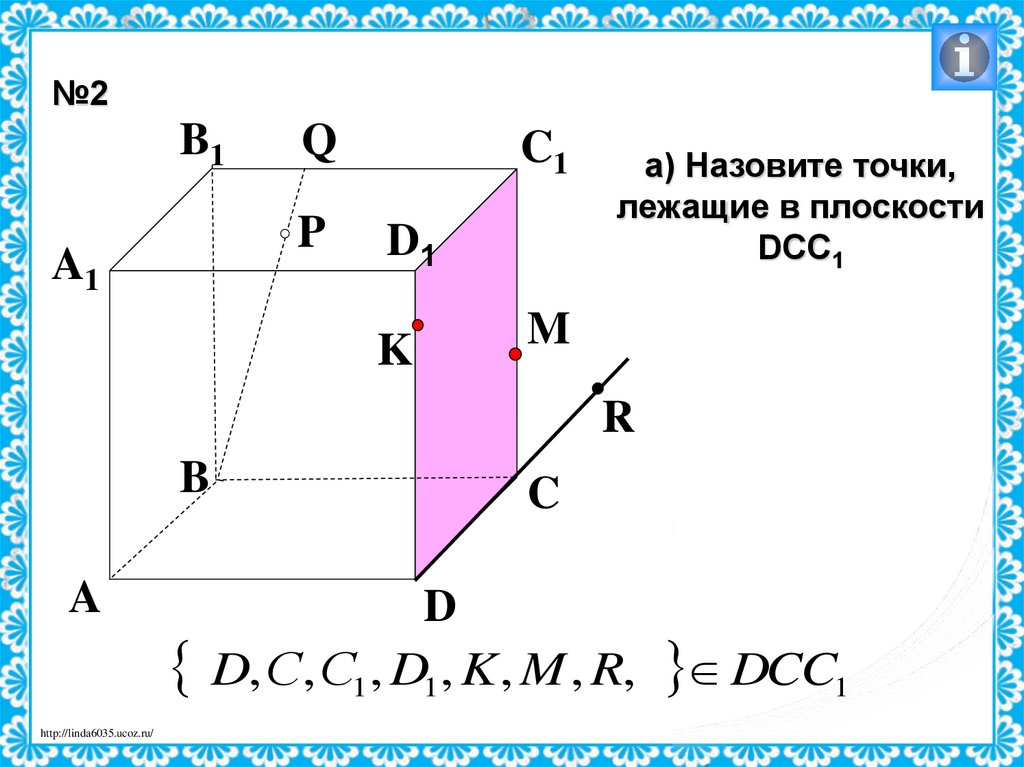
31.
№2B1
Q
P
A1
C1
D1
K
а) Назовите точки,
лежащие в плоскости
DCC1
M
R
B
A
http://linda6035.ucoz.ru/
C
D
D, С, С1, D1, K , M , R, DCC1
32.
B1Q
P
A1
C1
D1
K
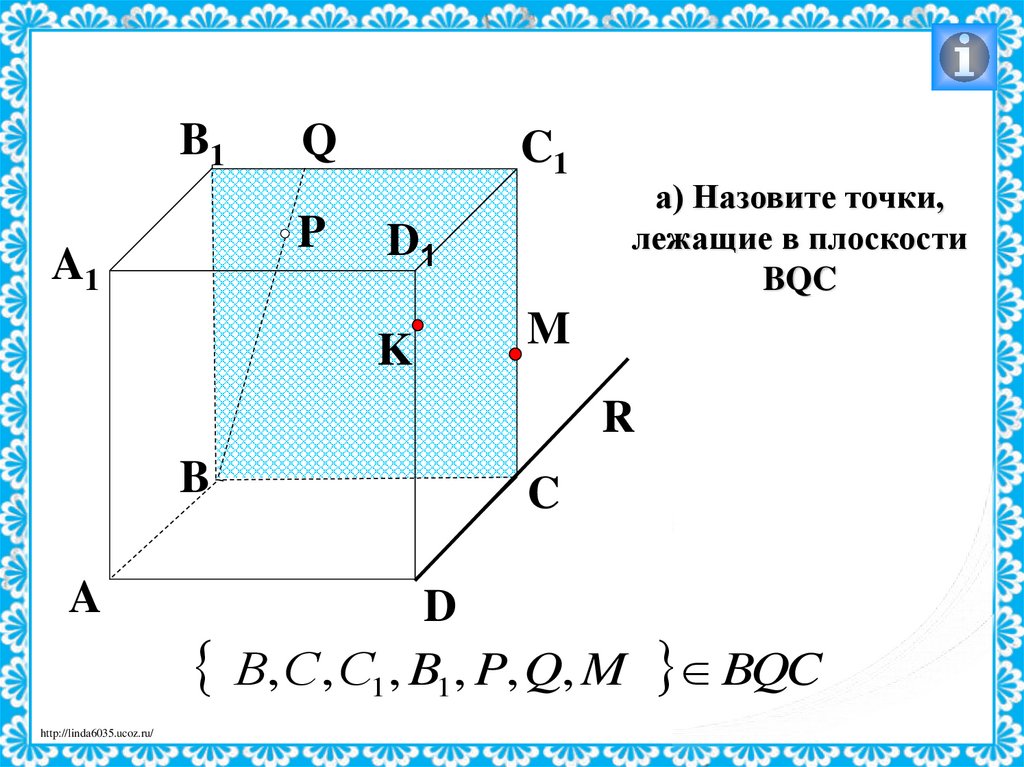
а) Назовите точки,
лежащие в плоскости
BQC
M
R
B
A
http://linda6035.ucoz.ru/
C
D
В, С, С1, B1, P, Q, M BQC
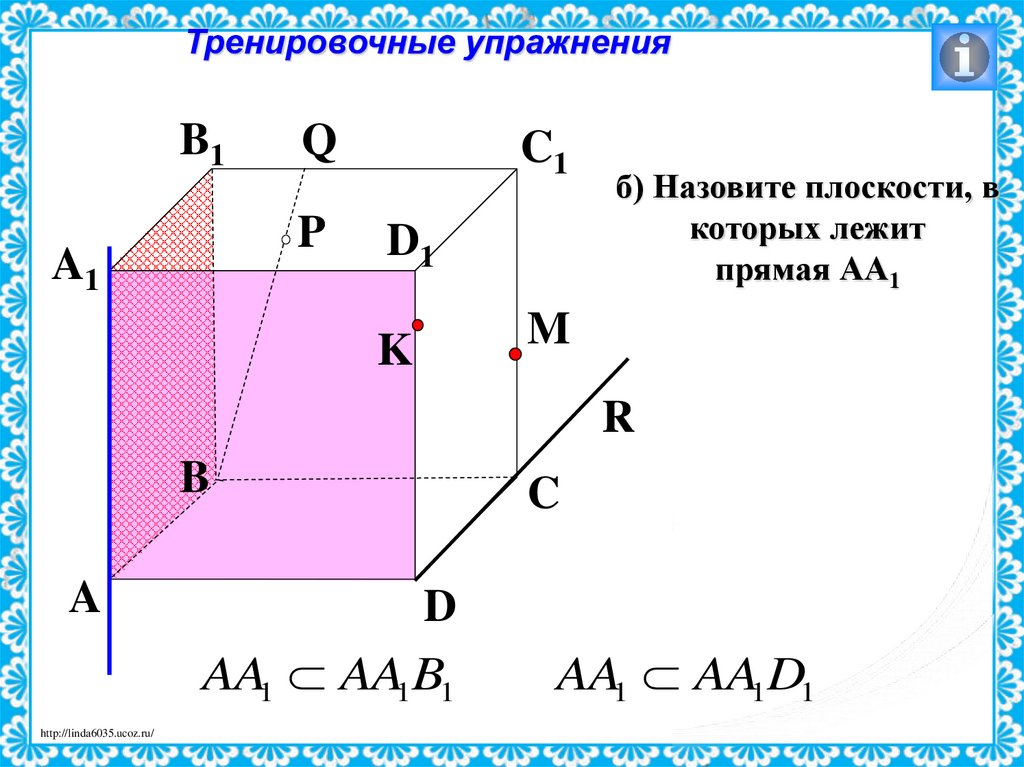
33.
Тренировочные упражненияB1
Q
P
A1
C1
D1
K
б) Назовите плоскости, в
которых лежит
прямая АА1
M
R
A
http://linda6035.ucoz.ru/
B
C
D
AA1 AA1B1
AA1 AA1D1
34.
B1Q
P
A1
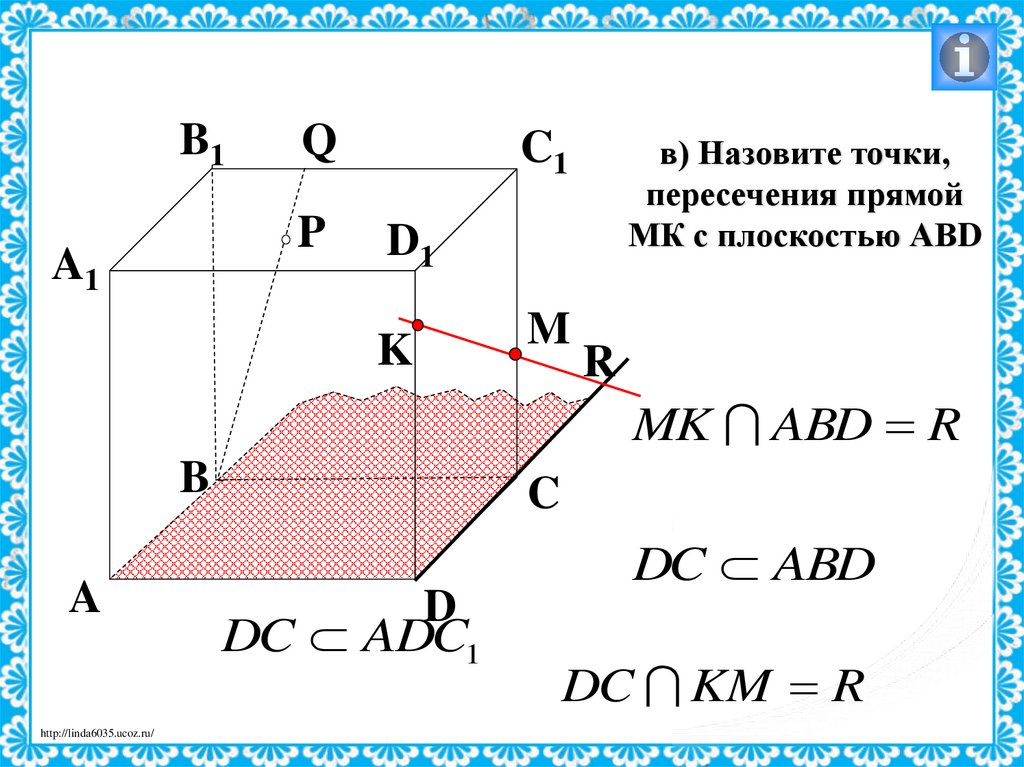
C1
в) Назовите точки,
пересечения прямой
МК с плоскостью АВD
D1
M
K
R
MK ABD R
B
A
http://linda6035.ucoz.ru/
C
D
DC ADC1
DC ABD
DC KM R
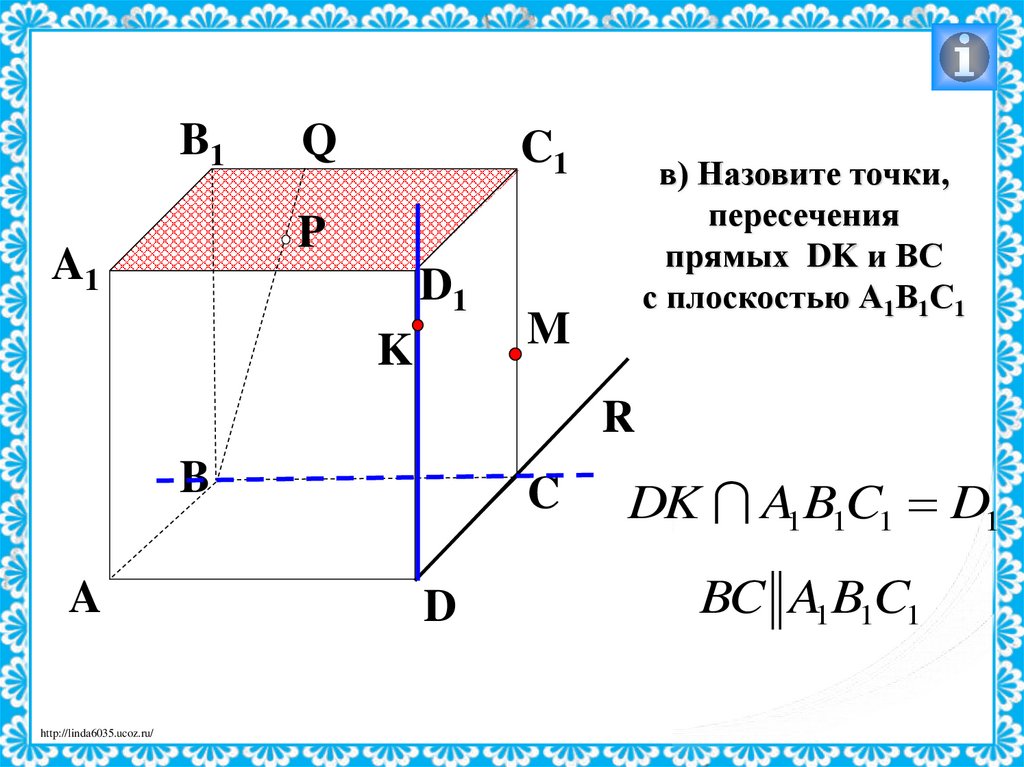
35.
B1Q
C1
в) Назовите точки,
пересечения
прямых DK и ВС
с плоскостью А1В1С1
P
A1
D1
K
M
R
B
A
http://linda6035.ucoz.ru/
C
D
DK A1B1C1 D1
BC A1B1C1
36.
B1Q
P
A1
C1
D1
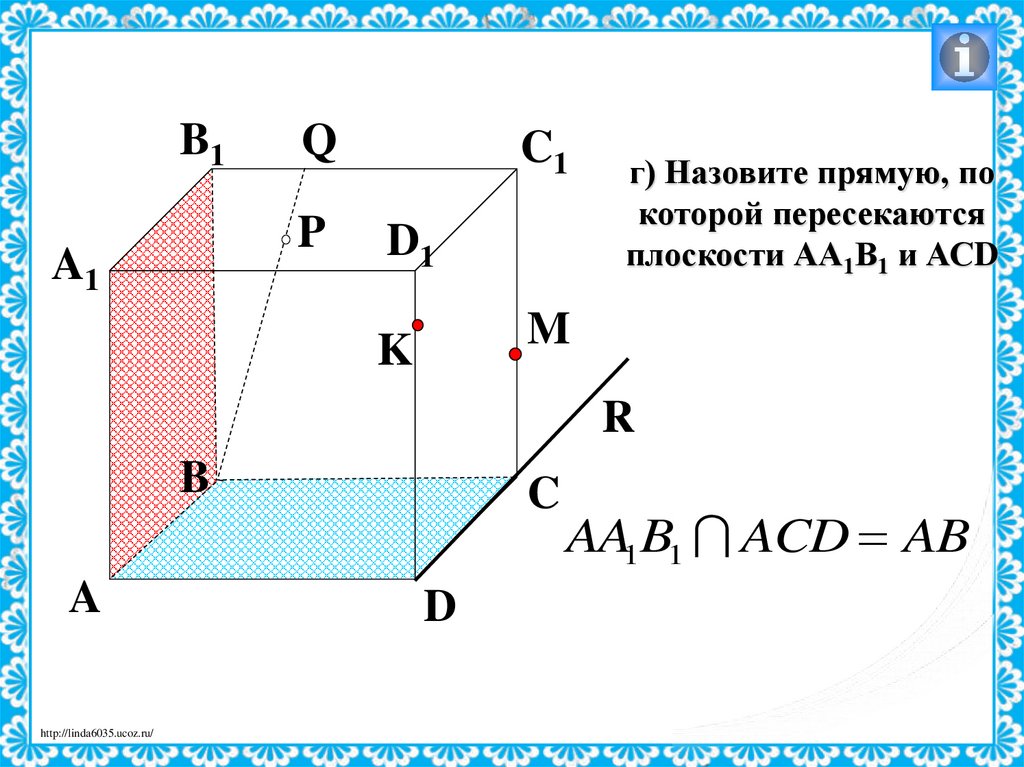
г) Назовите прямую, по
которой пересекаются
плоскости АА1В1 и АСD
M
K
R
B
A
http://linda6035.ucoz.ru/
C
D
AA1B1 ACD AB
37.
B1Q
P
A1
C1
D1
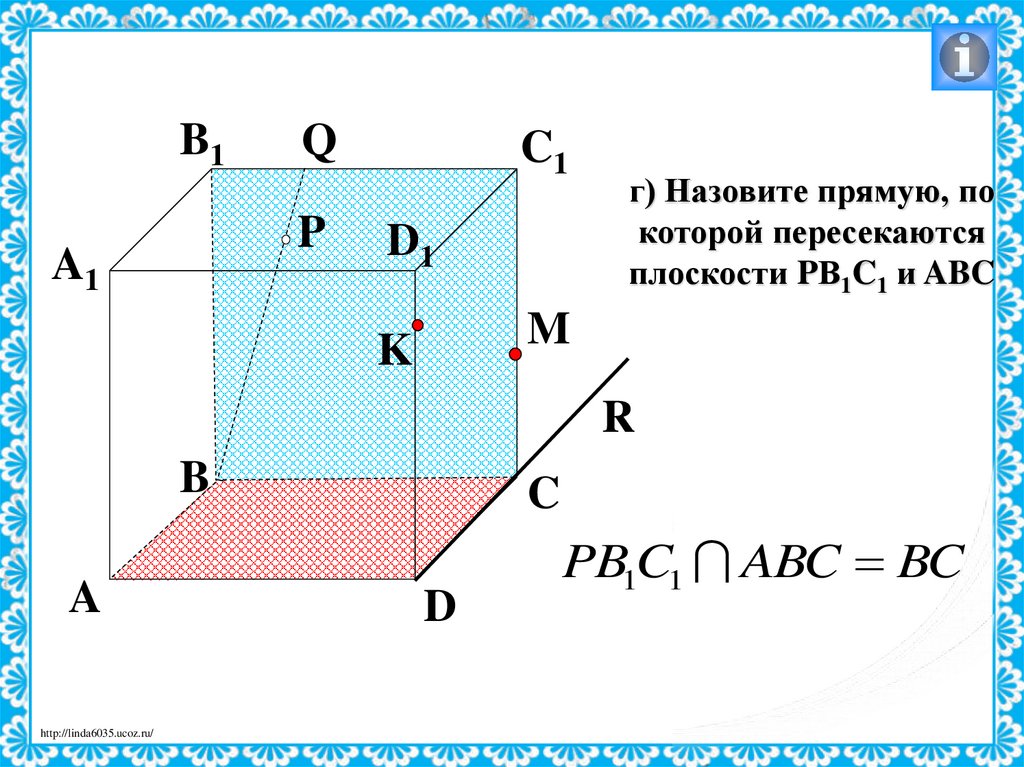
г) Назовите прямую, по
которой пересекаются
плоскости PВ1C1 и ABC
M
K
R
B
A
http://linda6035.ucoz.ru/
C
D
PB1C1 ABC BC
38.
B1Q
P
A1
C1
D1
M
K
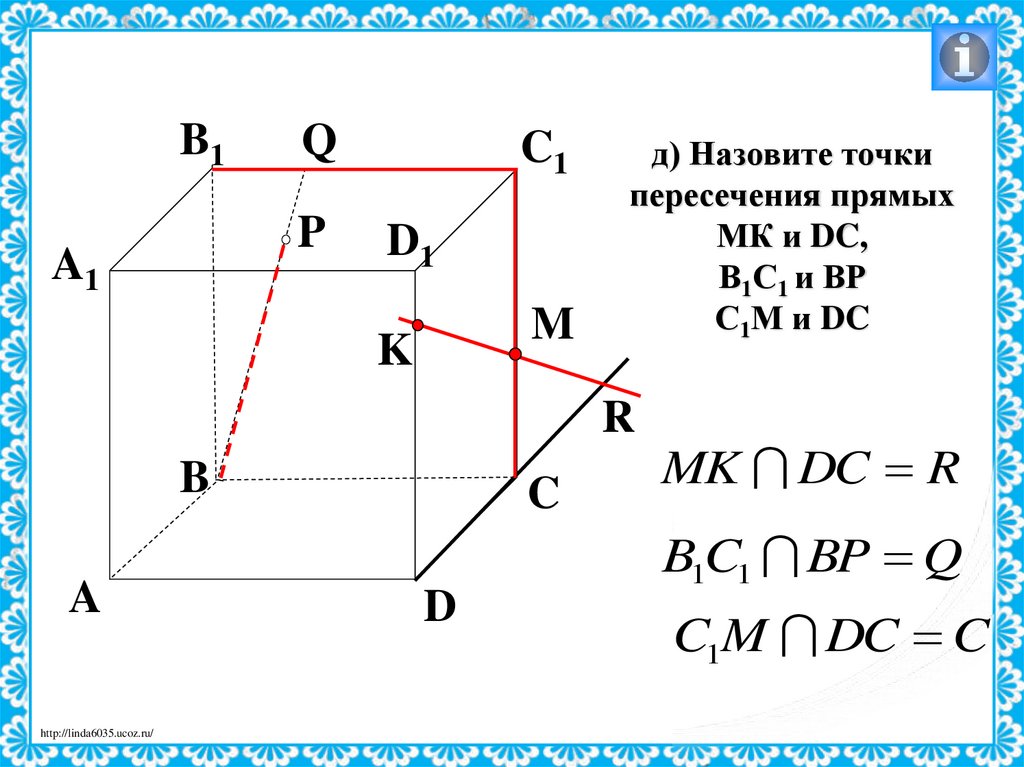
д) Назовите точки
пересечения прямых
МК и DC,
В1С1 и ВР
С1М и DC
R
B
A
http://linda6035.ucoz.ru/
C
D
MK DC R
B1C1 BP Q
C1M DC C
39.
Следствия из аксиомТеорема 1
(о прямой и точке)
Через прямую и не лежащую на ней точку
проходит плоскость, и притом только
одна.
Дано:
⍺
a
М
M a
Доказать:
! : M , a
http://linda6035.ucoz.ru/
40.
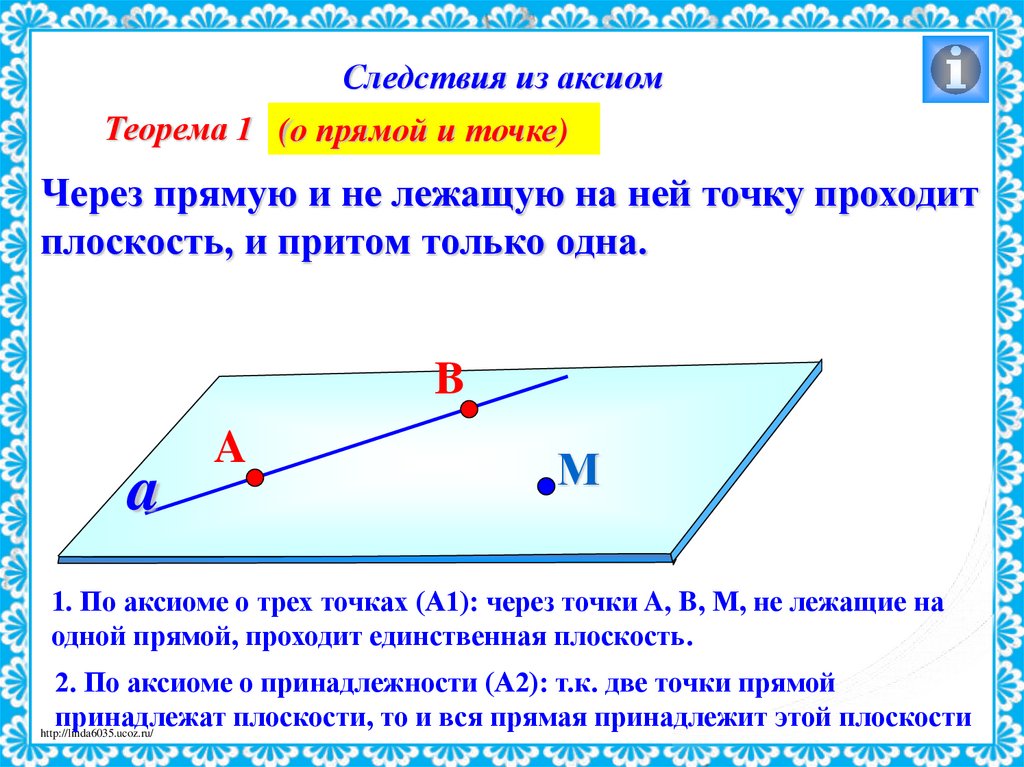
Следствия из аксиомТеорема 1 (о прямой и точке)
Через прямую и не лежащую на ней точку проходит
плоскость, и притом только одна.
B
a
A
М
1. По аксиоме о трех точках (А1): через точки A, B, М, не лежащие на
одной прямой, проходит единственная плоскость.
2. По аксиоме о принадлежности (А2): т.к. две точки прямой
принадлежат плоскости, то и вся прямая принадлежит этой плоскости
http://linda6035.ucoz.ru/
41.
http://linda6035.ucoz.ru/42.
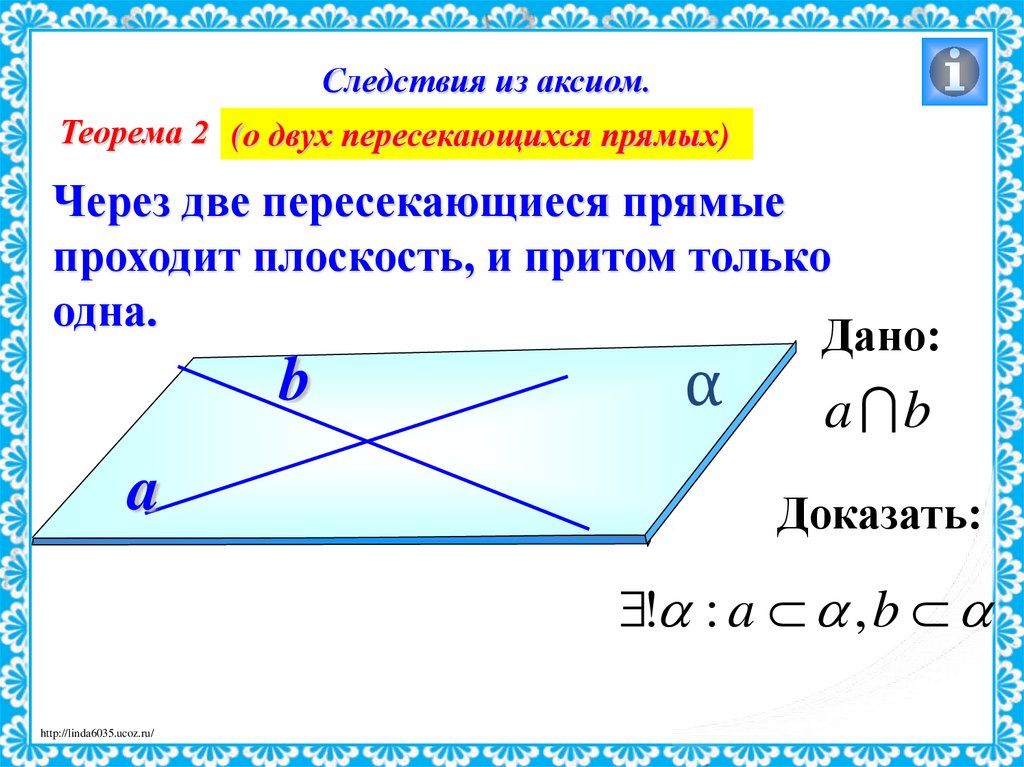
Следствия из аксиом.Теорема 2 (о двух пересекающихся прямых)
Через две пересекающиеся прямые
проходит плоскость, и притом только
одна.
Дано:
b
a
⍺
a b
Доказать:
! : a , b
http://linda6035.ucoz.ru/
43.
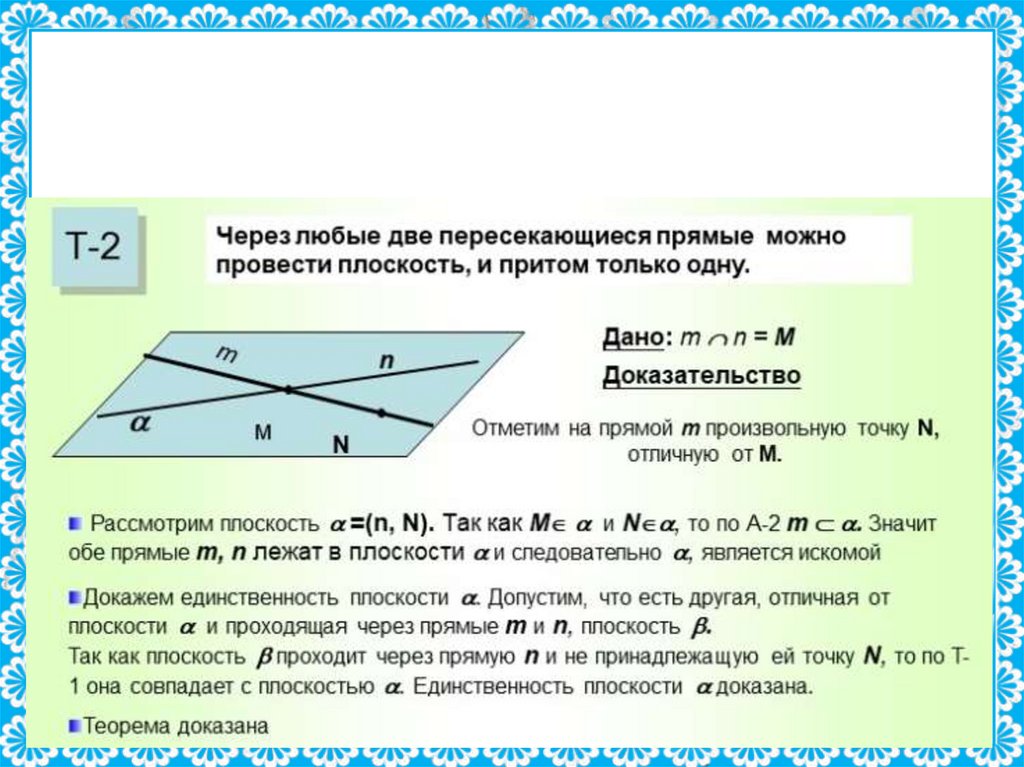
Следствия из аксиом.Теорема 2
(о двух пересекающихся прямых)
Через две пересекающиеся прямые проходит
плоскость, и притом только одна.
b M
a
N
1. По теореме 1 существует единственная плоскость, проходящая через
прямую и не лежащую на ней точку.
2. По аксиоме о принадлежности А2 прямая b лежит в плоскости
http://linda6035.ucoz.ru/
44.
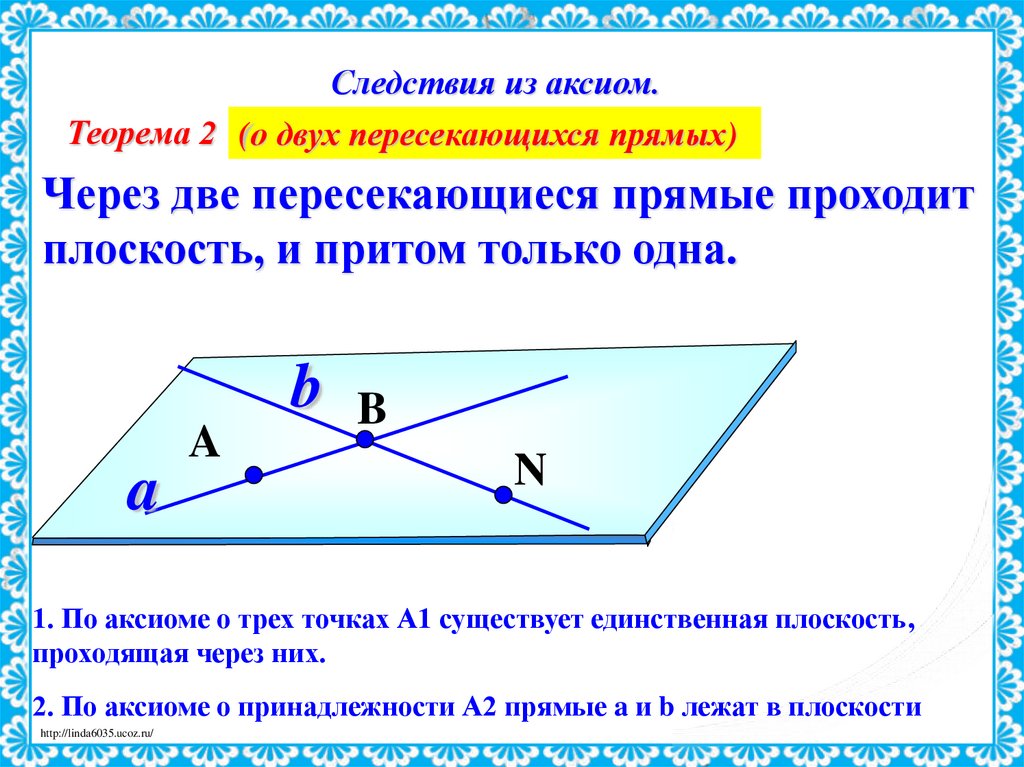
Следствия из аксиом.Теорема 2 (о двух пересекающихся прямых)
Через две пересекающиеся прямые проходит
плоскость, и притом только одна.
A
a
b B
N
1. По аксиоме о трех точках А1 существует единственная плоскость,
проходящая через них.
2. По аксиоме о принадлежности А2 прямые a и b лежат в плоскости
http://linda6035.ucoz.ru/
45.
http://linda6035.ucoz.ru/46.
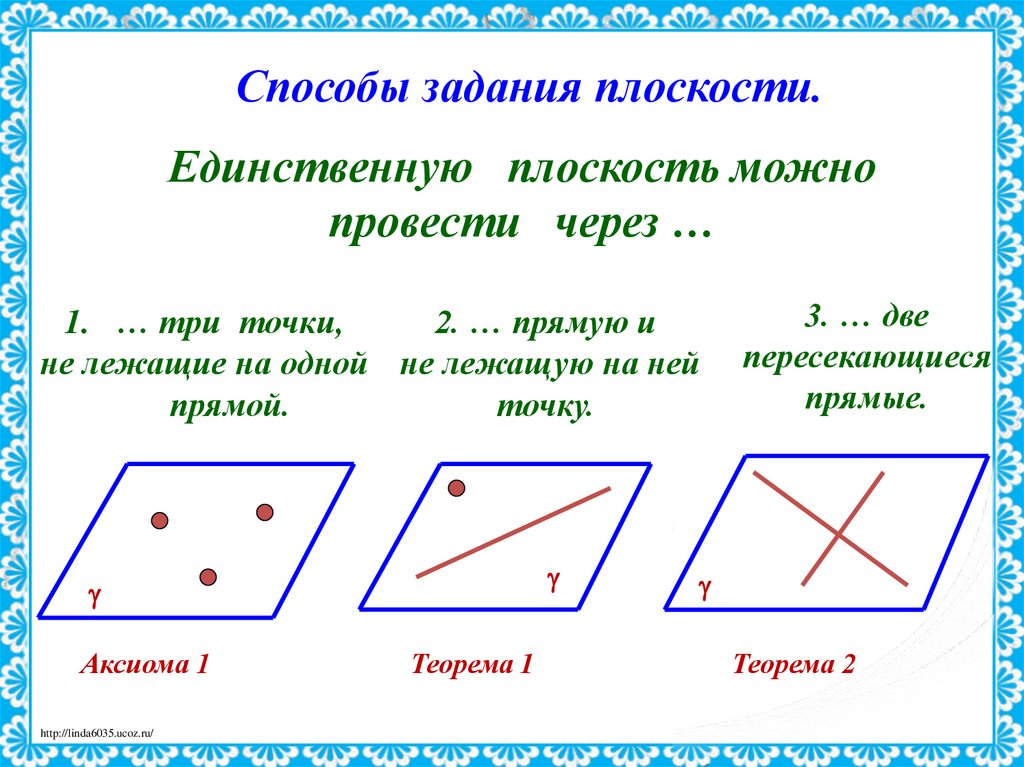
Способы задания плоскости.Единственную плоскость можно
провести через …
1. … три точки,
2. … прямую и
не лежащие на одной не лежащую на ней
прямой.
точку.
Аксиома 1
http://linda6035.ucoz.ru/
Теорема 1
3. … две
пересекающиеся
прямые.
Теорема 2













 mathematics
mathematics








