Similar presentations:
П- ТРЕУГОЛЬНИКИ ЕГЭ
1.
ГЕОМЕТРИЯПланиметрия
Часть 1. Треугольники
РЕПЕТИТОР Султанова М.М.
2. Рекомендации ученикам
По каждой теме:1. Изучайте презентацию, смотрите
видеоролики.
2. Решайте самостоятельную работу
После изучения всех тем – решайте подборку
задач из ЕГЭ за 26 год.
Задачи из банка ФИПИ решайте в течение года
3. Задание 3. План изучения темы
1. Треугольники1.
2.
3.
Прямоугольный треугольники
Равнобедренный треугольник
Произвольный треугольник
2. Четырехугольники
1. Трапеция
2. Параллелограмм и ромб
3. Прямоугольник и квадрат
3. Окружность и углы
4. Вписанные и описанные окружности
1.
2.
3.
Окружность + треугольник
Окружность + четырехугольник
Окружность + шестиугольник
4. 1.1. Прямоугольный треугольник
a, b - катетыс - гипотенуза
c
а
sin =
противолежащий катет
гипотенуза
=
a
c
=
b
c
b
a
b
c
ctg =
cos =
tg =
прилежащий катет
гипотенуза
противолежащий катет
прилежащий катет
противолежащий катет
прилежащий катет
=
b
a
=
a
b
5. 1.1. Прямоугольный треугольник
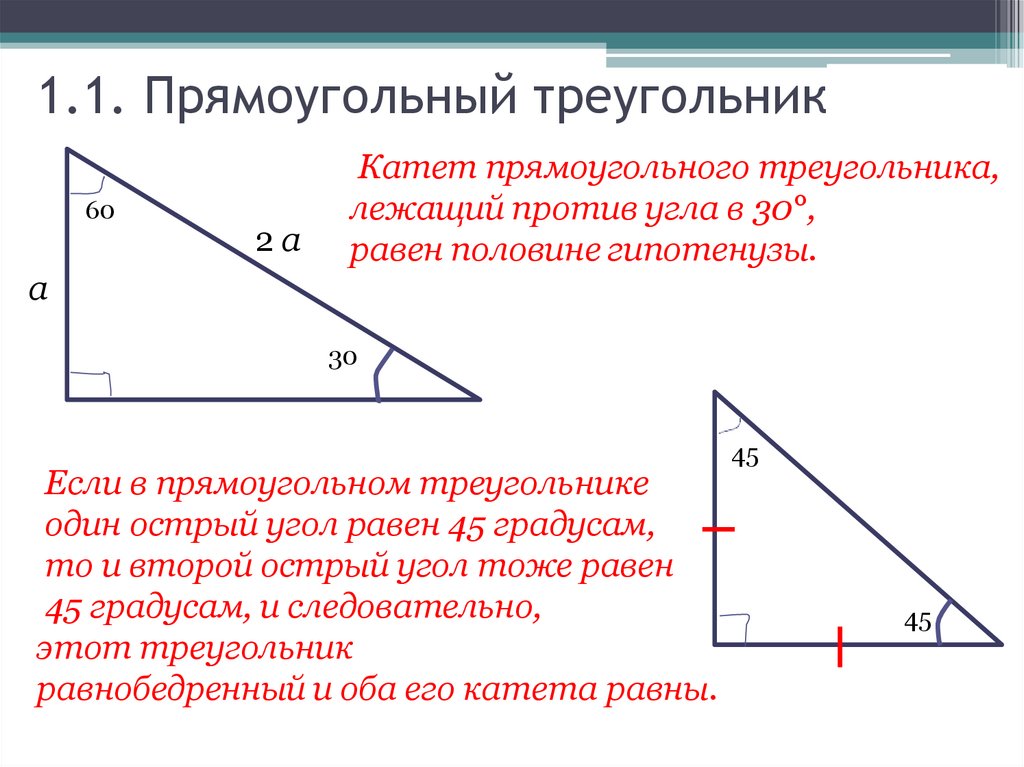
602a
Катет прямоугольного треугольника,
лежащий против угла в 30°,
равен половине гипотенузы.
a
30
Если в прямоугольном треугольнике
один острый угол равен 45 градусам,
то и второй острый угол тоже равен
45 градусам, и следовательно,
этот треугольник
равнобедренный и оба его катета равны.
45
45
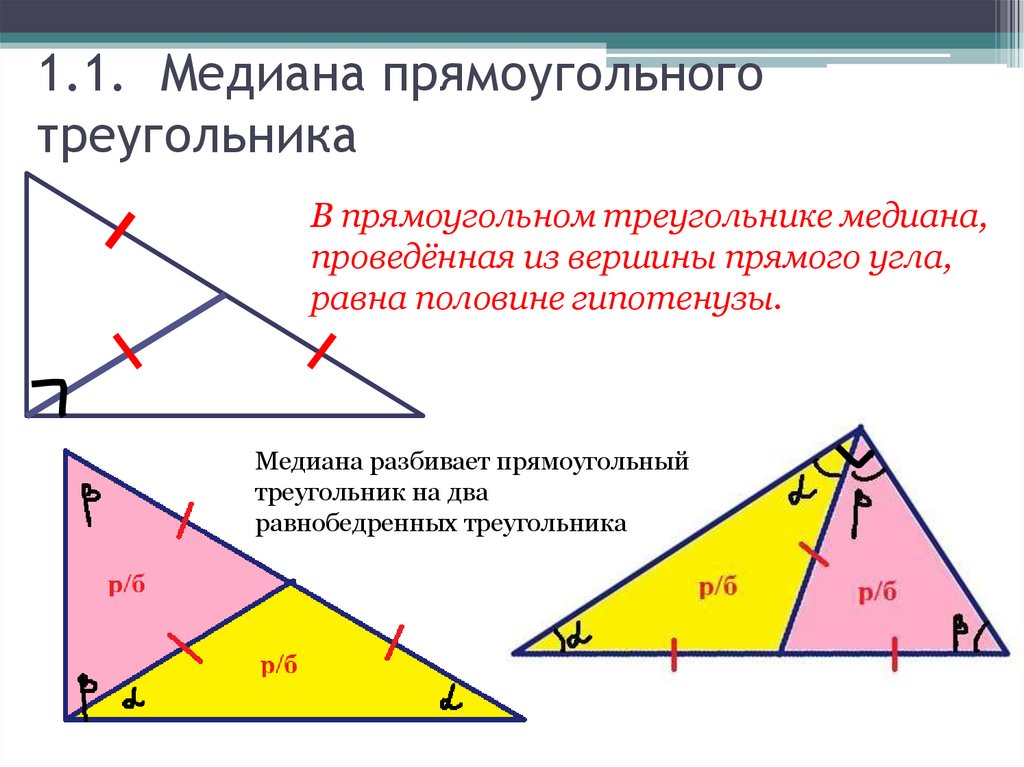
6. 1.1. Медиана прямоугольного
треугольникаВ прямоугольном треугольнике медиана,
проведённая из вершины прямого угла,
равна половине гипотенузы.
Медиана разбивает прямоугольный
треугольник на два
равнобедренных треугольника
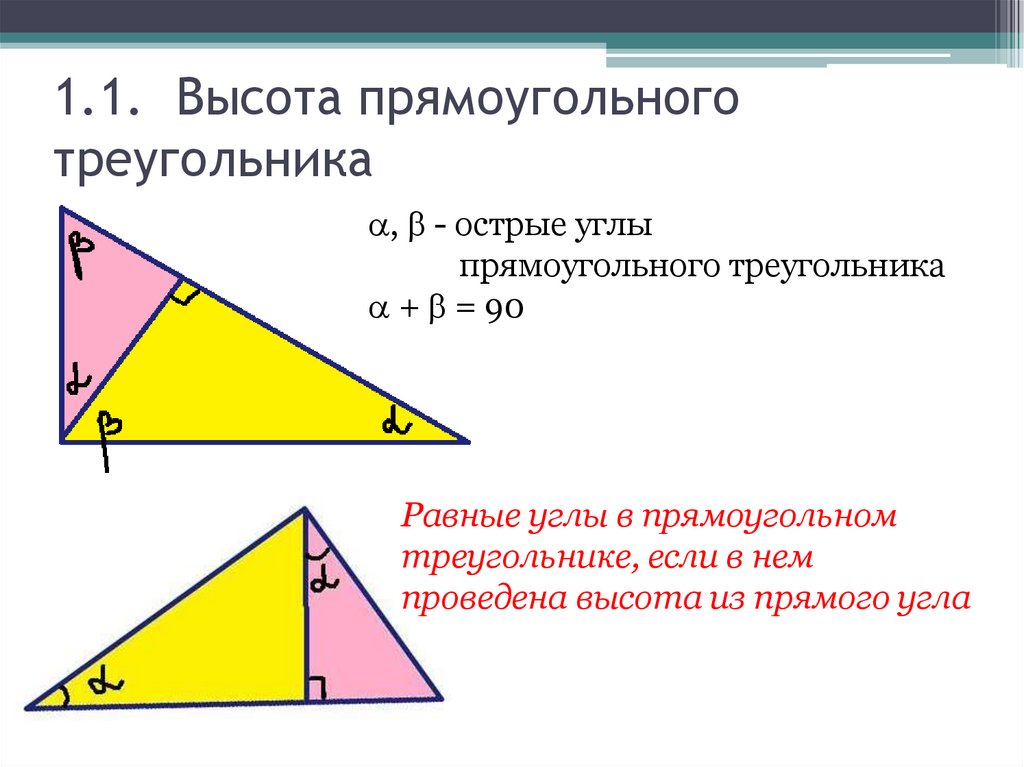
7. 1.1. Высота прямоугольного треугольника
, - острые углыпрямоугольного треугольника
+ = 90
Равные углы в прямоугольном
треугольнике, если в нем
проведена высота из прямого угла
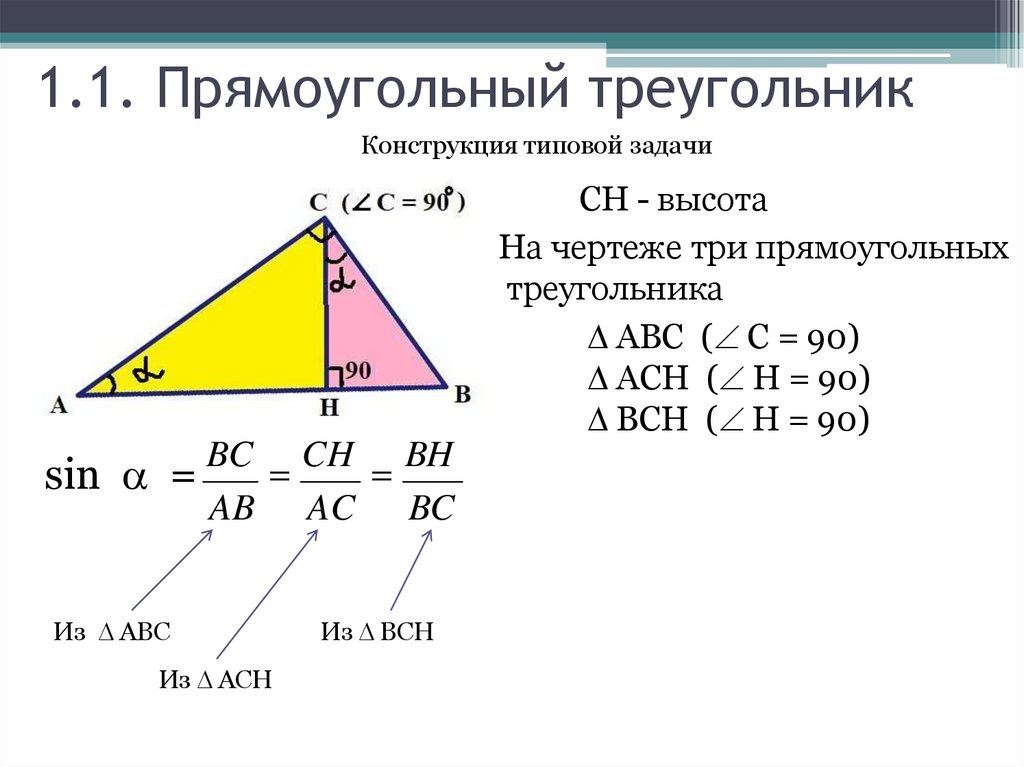
8. 1.1. Прямоугольный треугольник
Конструкция типовой задачиCH - высота
На чертеже три прямоугольных
треугольника
ABC ( C = 90)
ACH ( H = 90)
BCH ( H = 90)
sin =
BC CH BH
AB AC BC
Из АВС
Из АСH
Из BCH
9.
10. 1.1. Взаимосвязь тригонометрических
функцийНапример, вам известен
тангенс,
а хотите найти косинус
tg = 3
cos - ?
Есть два способа
2 способ
С помощью прямоугольного
треугольника
1 способ
Тригонометрические
формулы
sin 2 cos 2 1
1
cos 2
sin
tg
cos
1 tg 2
32 1 2 10
sin
3
1
3
10
1
cos
10
11. 1.1. Прямоугольный треугольник
1 5 26sin
1
5
cos
2
1
tg
5
sin
2
BC
AB
26
BC
13
13
26
26
cos CH
CB
26
CH
BC
26
5
(из BCH)
5
1
1
CH
13 / 26
65
1
26 26
CH 2,5
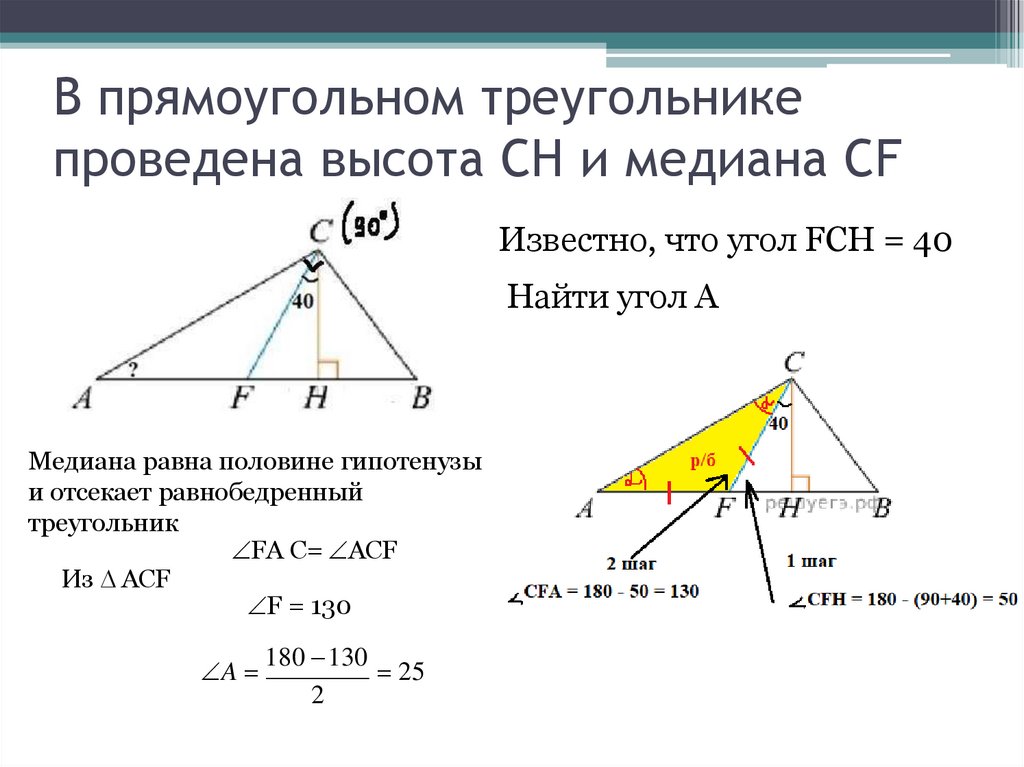
12. В прямоугольном треугольнике проведена высота CH и медиана CF
Известно, что угол FCH = 40Найти угол А
Медиана равна половине гипотенузы
и отсекает равнобедренный
треугольник
FA C= ACF
Из ACF
F = 130
A
180 130
25
2
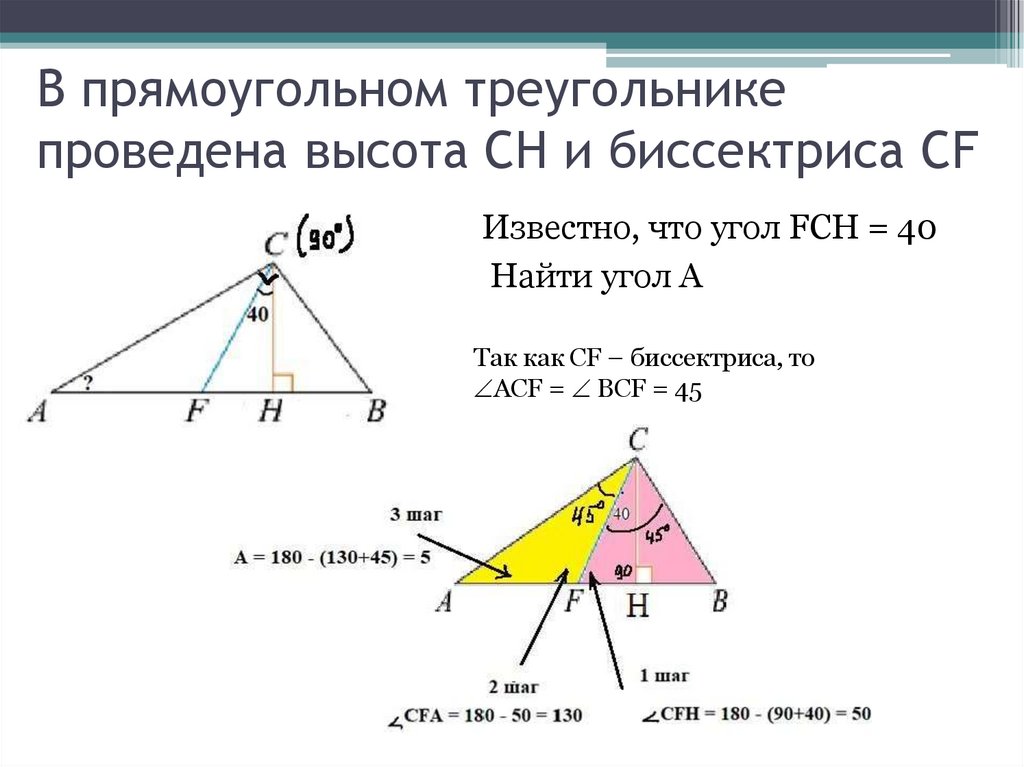
13. В прямоугольном треугольнике проведена высота CH и биссектриса CF
Известно, что угол FCH = 40Найти угол А
Так как CF – биссектриса, то
АСF = BCF = 45
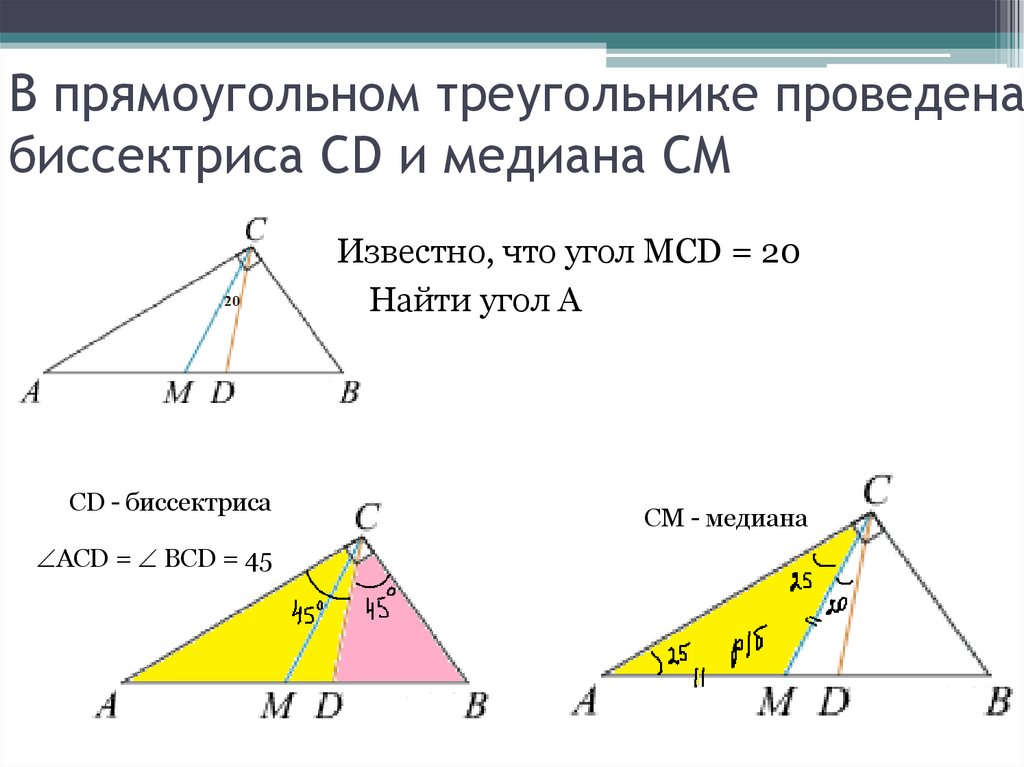
14. В прямоугольном треугольнике проведена
биссектриса CD и медиана СМИзвестно, что угол MCD = 20
Найти угол А
CD - биссектриса
АСD = BCD = 45
СМ - медиана
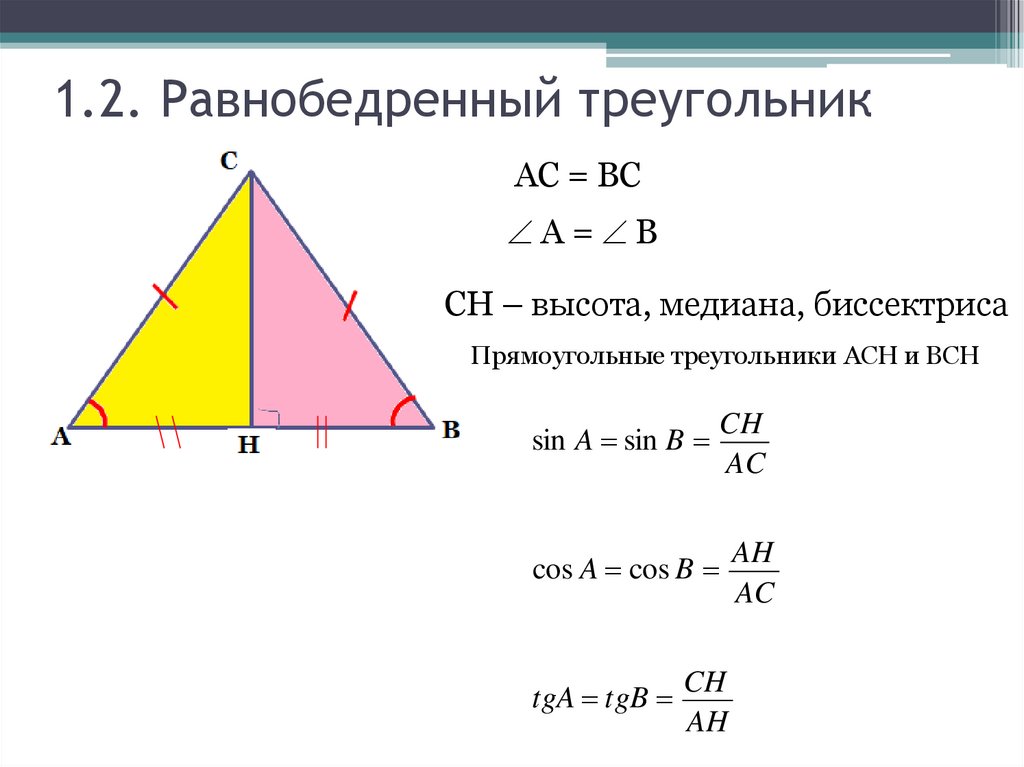
15. 1.2. Равнобедренный треугольник
АС = ВСА= В
СН – высота, медиана, биссектриса
Прямоугольные треугольники ACH и BCH
sin A sin B
CH
AC
cos A cos B
tgA tgB
CH
AH
AH
AC
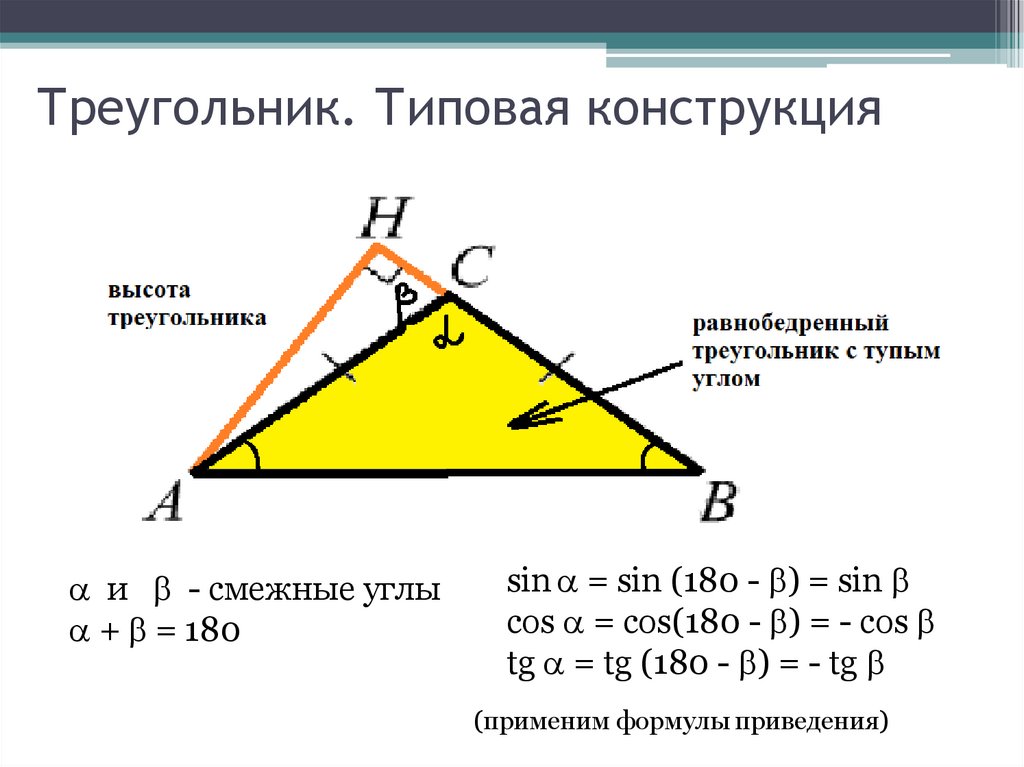
16. Треугольник. Типовая конструкция
и - смежные углы+ = 180
sin = sin (180 - ) = sin
cos = cos(180 - ) = - cos
tg = tg (180 - ) = - tg
(применим формулы приведения)
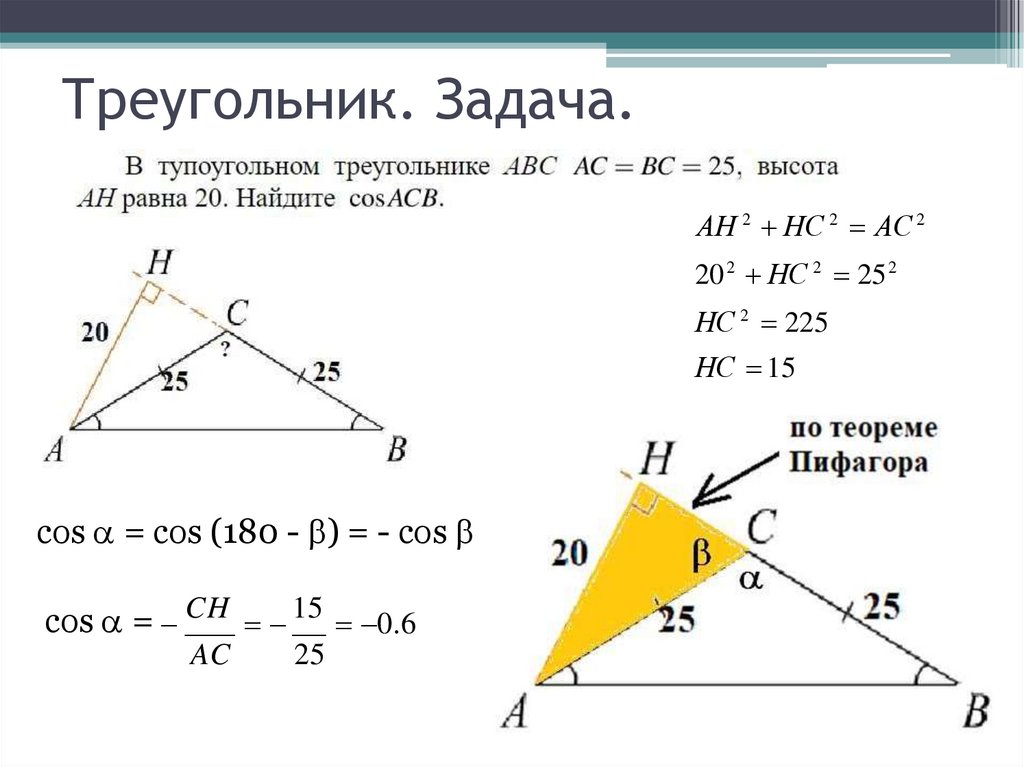
17. Треугольник. Задача.
АН 2 НС 2 АС 220 2 НС 2 25 2
НС 2 225
НС 15
cos = cos (180 - ) = - cos
cos = CH 15 0.6
AC
25
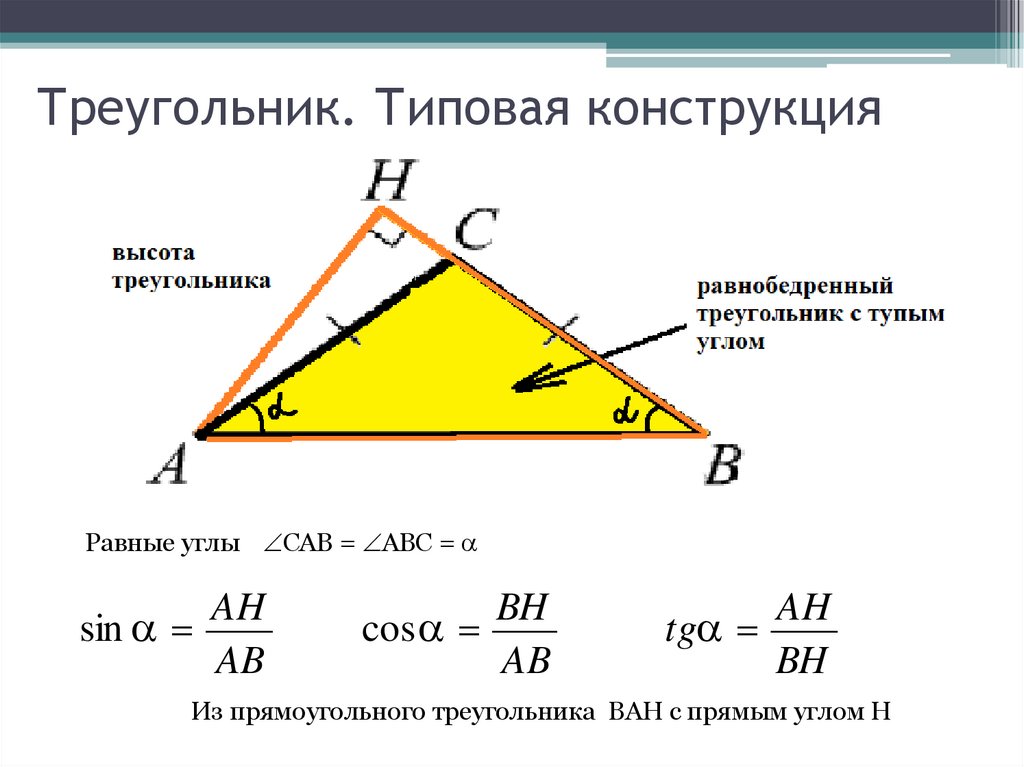
18. Треугольник. Типовая конструкция
Равные углы САВ = АВС =AH
sin
AB
BH
cos
AB
AH
tg
BH
Из прямоугольного треугольника BAH c прямым углом Н
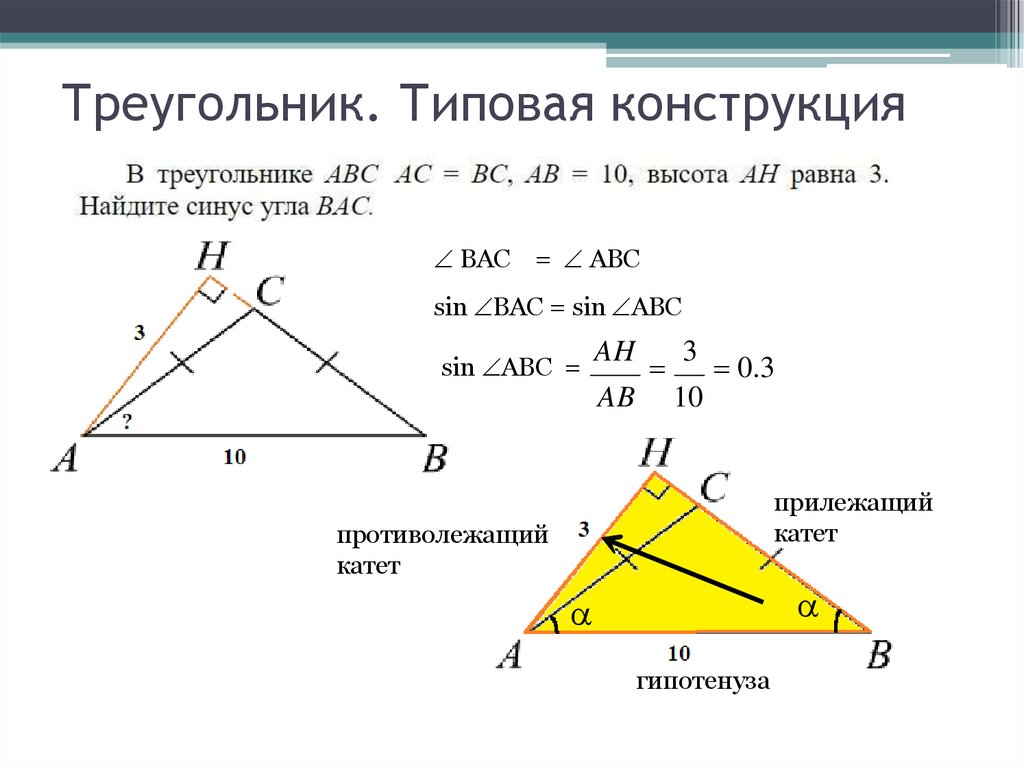
19. Треугольник. Типовая конструкция
BAC = ABCsin BAC = sin ABC
sin ABC =
AH
AB
3
0.3
10
прилежащий
катет
противолежащий
катет
гипотенуза
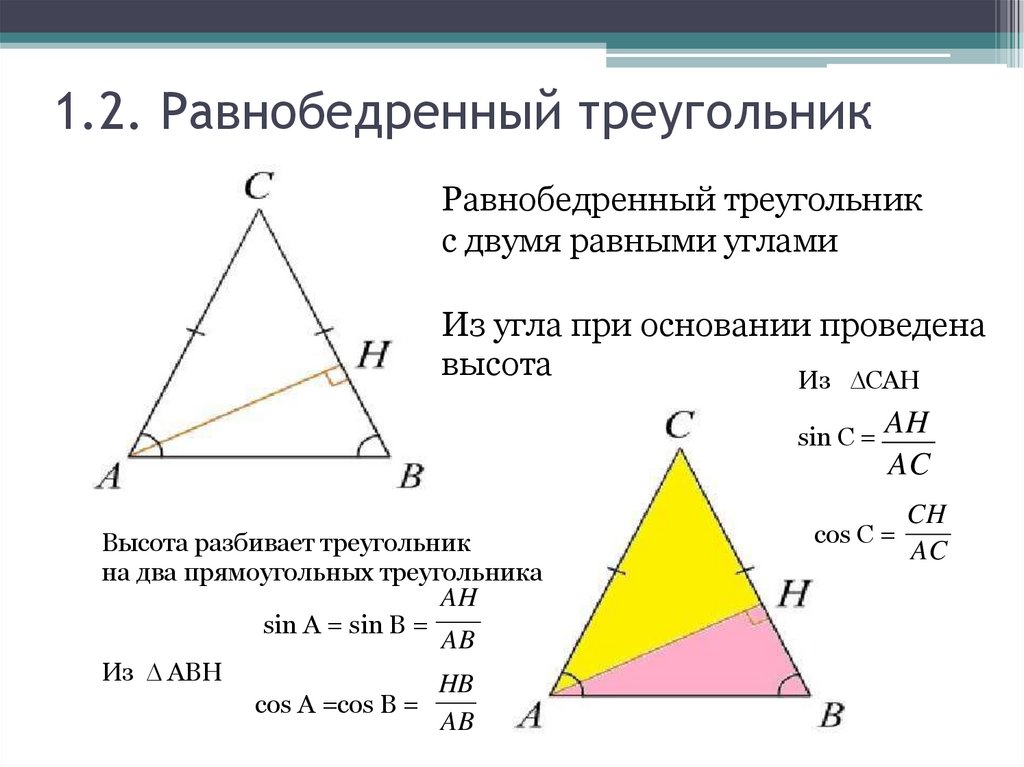
20. 1.2. Равнобедренный треугольник
Равнобедренный треугольникс двумя равными углами
Из угла при основании проведена
высота
Из CAH
sin C =
Высота разбивает треугольник
на два прямоугольных треугольника
sin A = sin B =
Из ABH
AH
AB
HB
cos A =cos B =
AB
AH
AC
CH
cos C =
AC
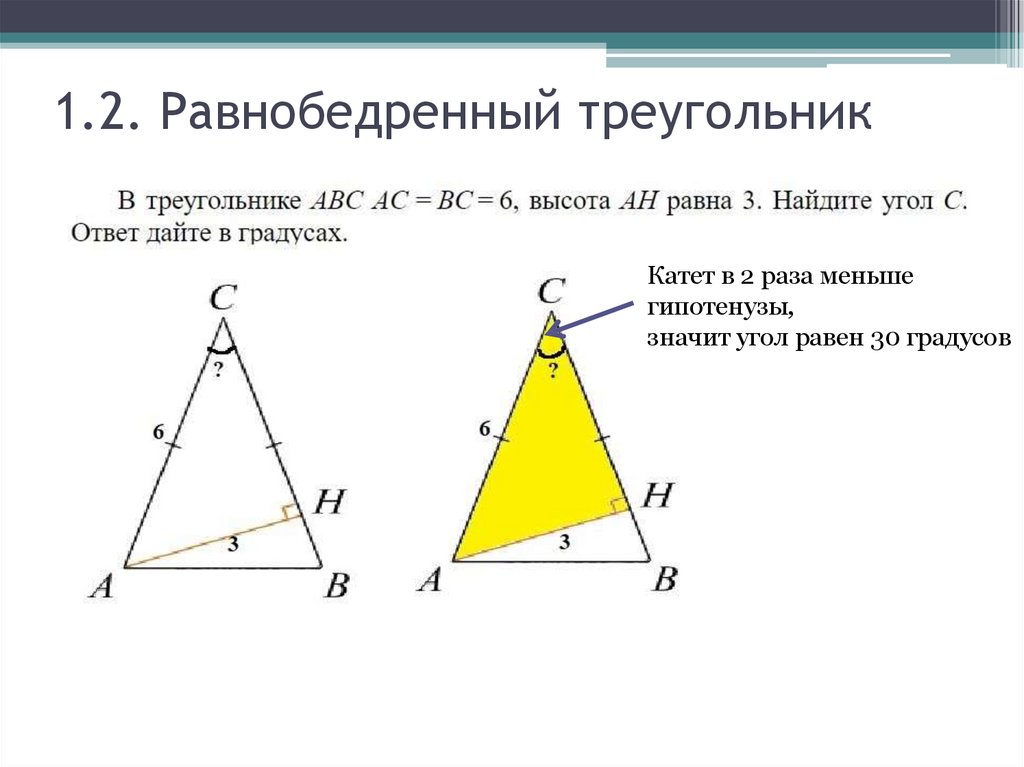
21. 1.2. Равнобедренный треугольник
Катет в 2 раза меньшегипотенузы,
значит угол равен 30 градусов
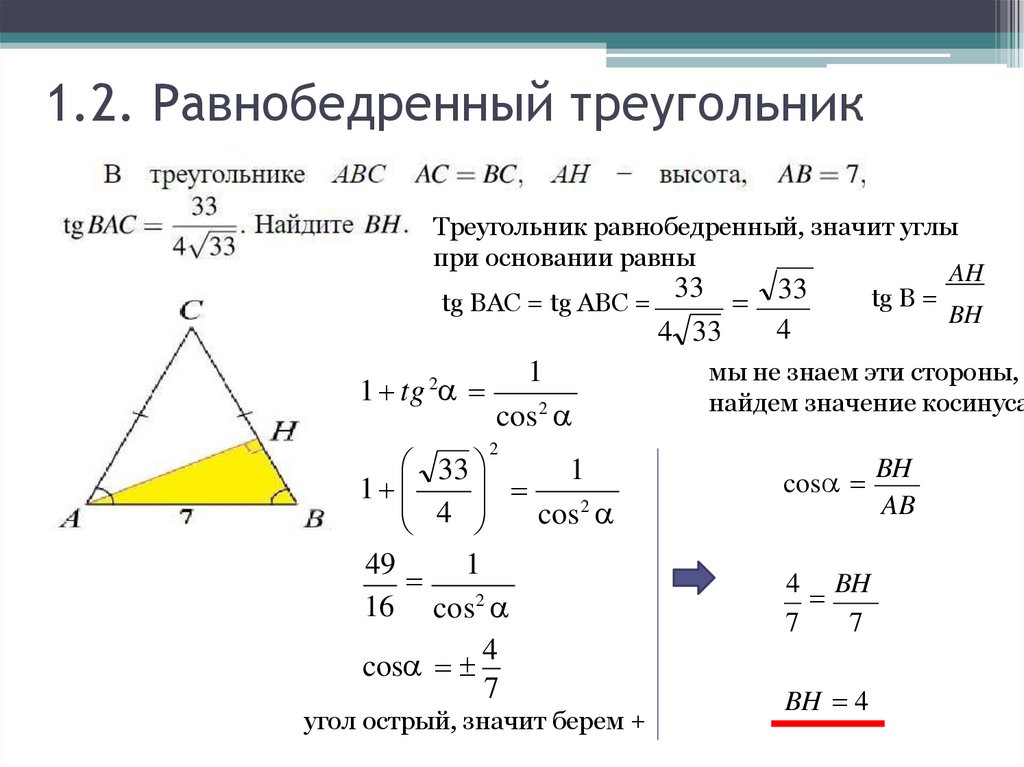
22. 1.2. Равнобедренный треугольник
Треугольник равнобедренный, значит углыпри основании равны
AH
33
33
tg B =
tg BAC = tg ABC =
BH
4 33
1 tg 2
1
cos2
4
мы не знаем эти стороны,
найдем значение косинуса
2
33
1
1
cos2
4
49
1
16 cos2
4
cos
7
угол острый, значит берем +
cos
4 BH
7
7
BH 4
BH
AB
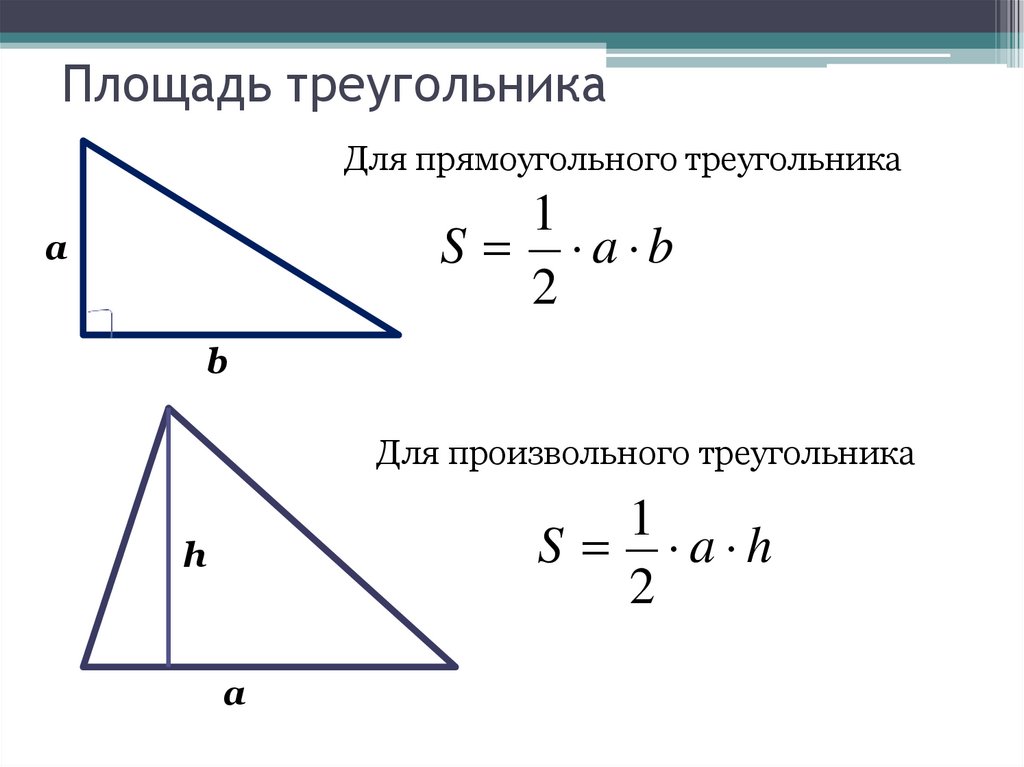
23. Площадь треугольника
Для прямоугольного треугольника1
S a b
2
а
b
Для произвольного треугольника
1
S a h
2
h
а
24. Задача. Площадь треугольника
Боковая сторона равнобедренного треугольникаравна 5, а основание равно 6.
Найдите площадь этого треугольника.
1 способ:
32 h 2 5 2
S 1 a h
2
h 4
5
5
S
h
2 способ:
3
3
1
4 6 12
2
Формула Герона
S
p
5 5 6
8
2
p
p ( p a) ( p b) ( p c)
a b c
2
S 8 (8 5) (8 5) (8 6) 8 3 3 2 12
25. Площадь треугольника
1S a b sin
2
а
b
Угол при вершине, противолежащей основанию равнобедренного
треугольника, равен 150°.
20
Боковая сторона треугольника равна 20.
20
150
Найдите площадь этого треугольника.
S
1
2
20 20 sin 150 200 sin(180 30) 200 sin 30 200
1
2
100
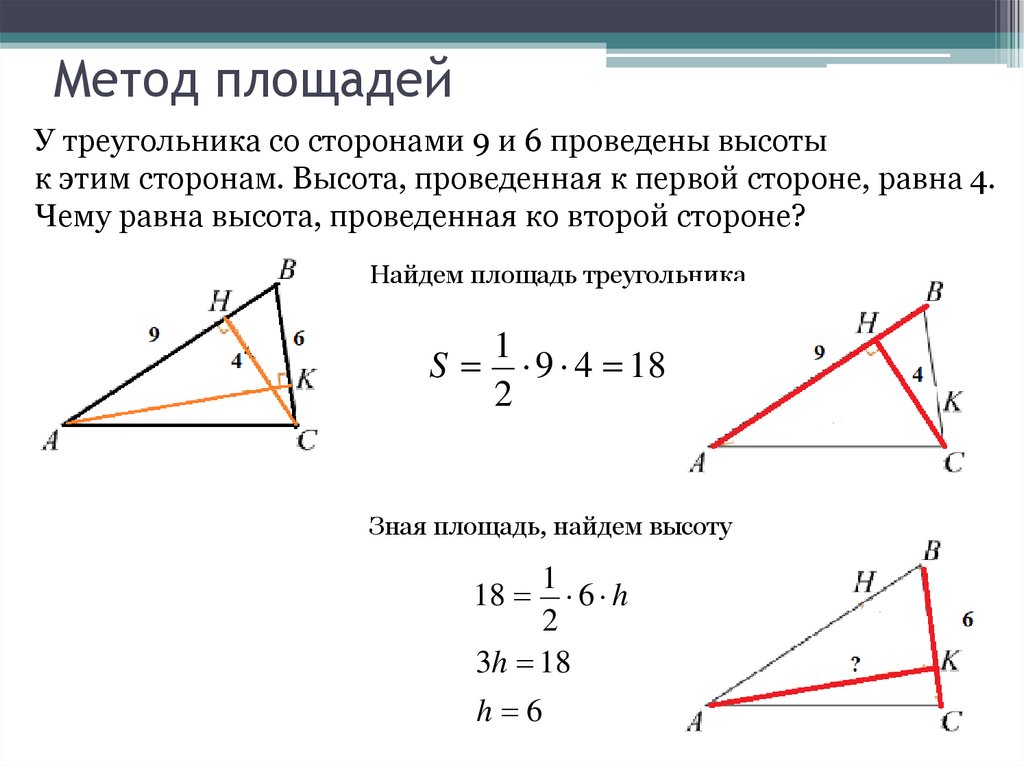
26. Метод площадей
У треугольника со сторонами 9 и 6 проведены высотык этим сторонам. Высота, проведенная к первой стороне, равна 4.
Чему равна высота, проведенная ко второй стороне?
Найдем площадь треугольника
1
S 9 4 18
2
Зная площадь, найдем высоту
1
6 h
2
3h 18
18
h 6
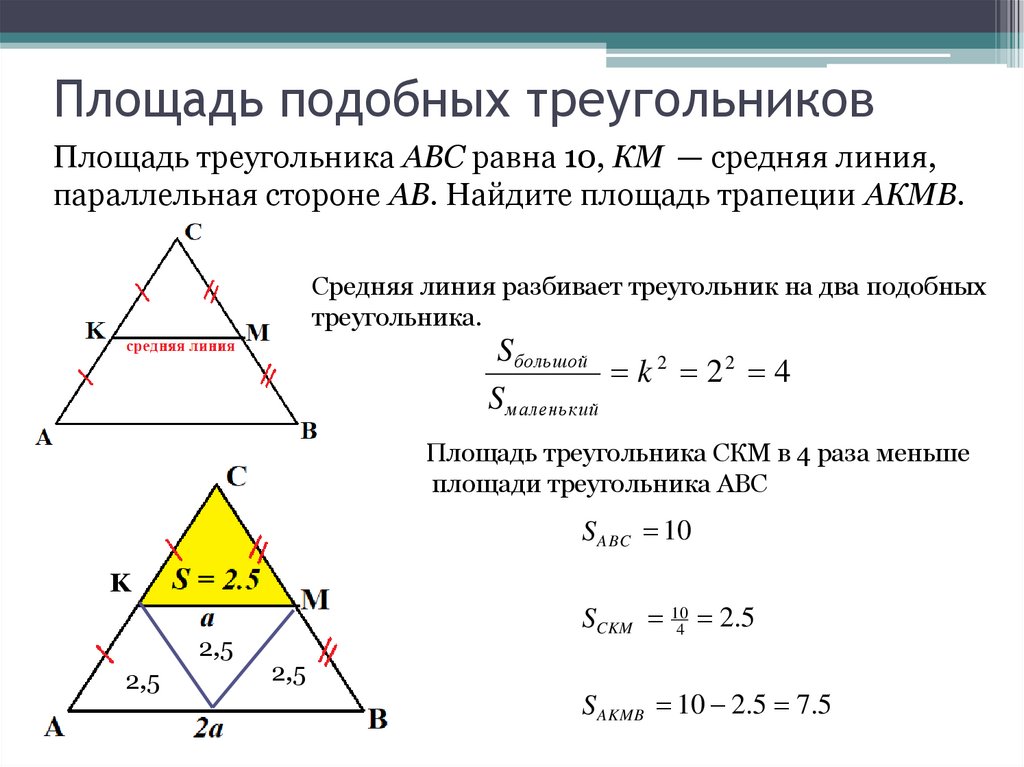
27. Площадь подобных треугольников
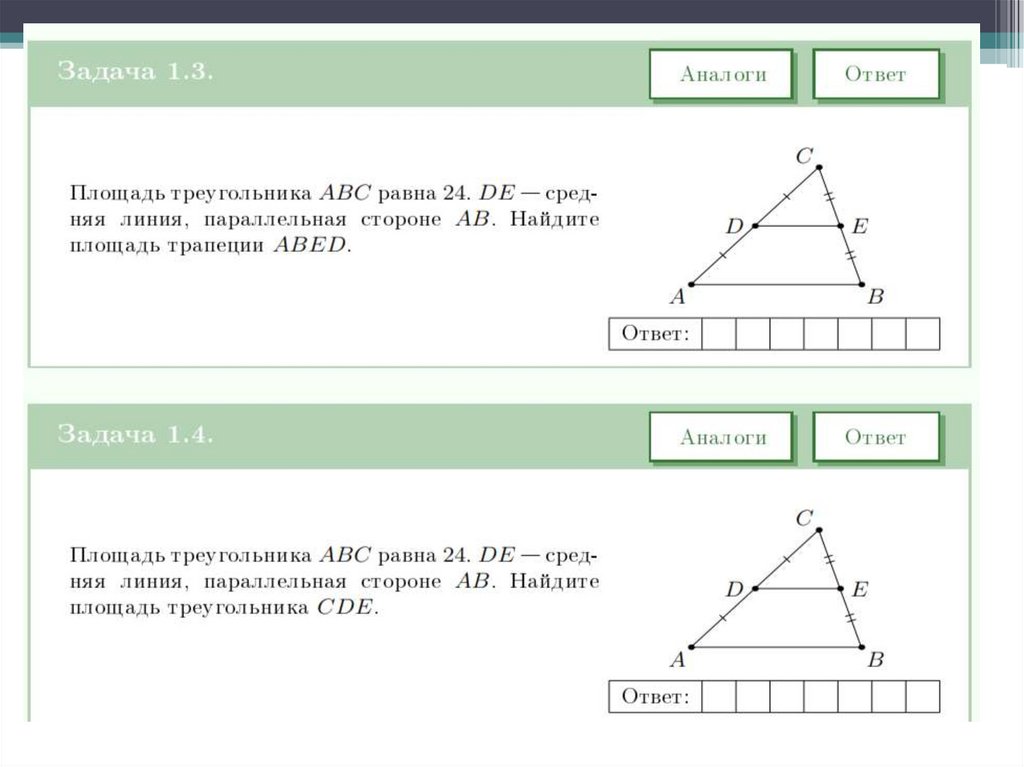
Площадь треугольника ABC равна 10, КМ — средняя линия,параллельная стороне AB. Найдите площадь трапеции AКМВ.
Средняя линия разбивает треугольник на два подобных
треугольника.
Sбольшой
k 2 22 4
Sмаленький
Площадь треугольника СКМ в 4 раза меньше
площади треугольника АВС
S ABC 10
K
2,5
2,5
SCKM 104 2.5
2,5
S AKMB 10 2.5 7.5
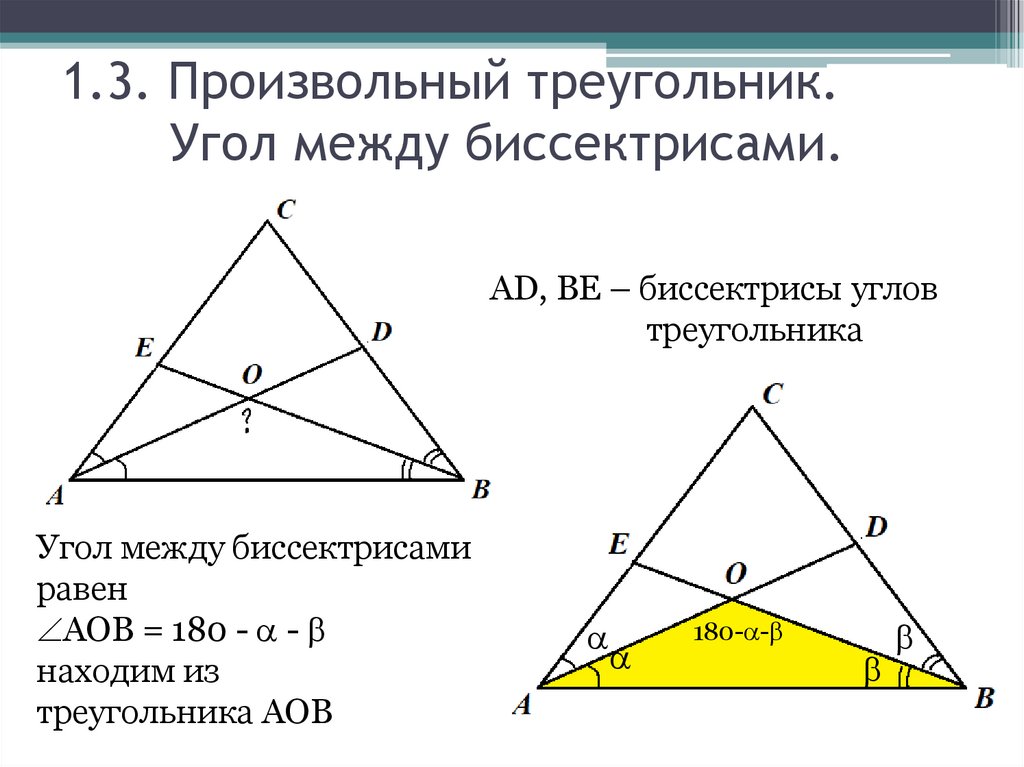
28. 1.3. Произвольный треугольник.
Угол между биссектрисами.AD, BE – биссектрисы углов
треугольника
Угол между биссектрисами
равен
АОВ = 180 - -
находим из
треугольника АОВ
180- -
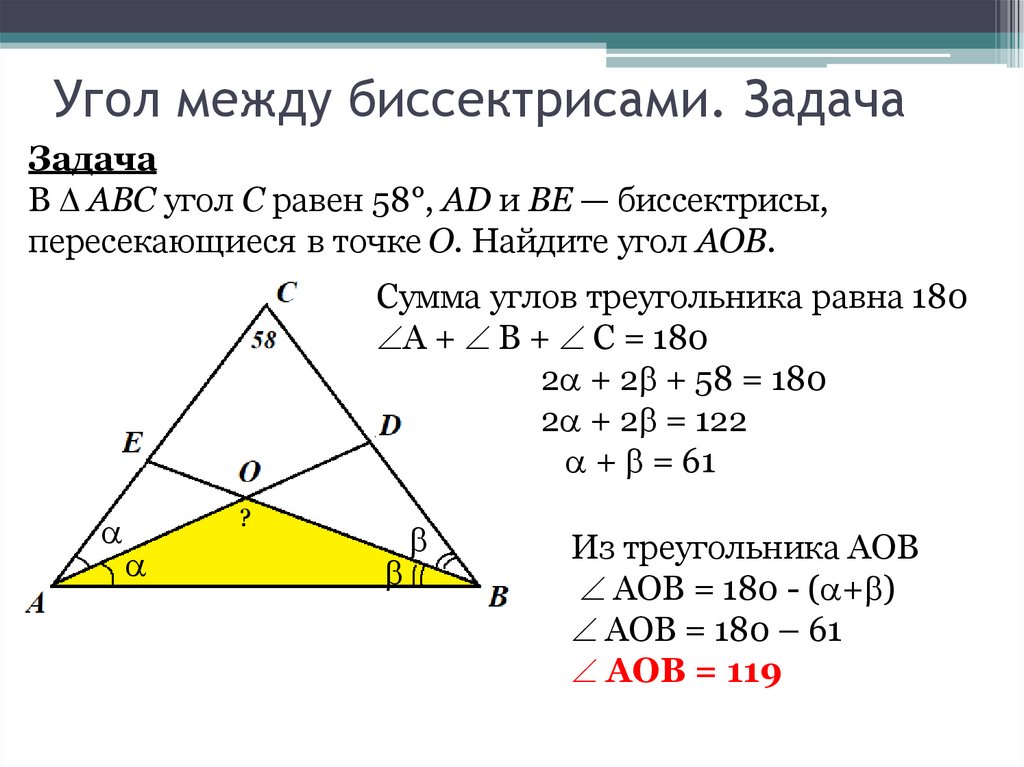
29. Угол между биссектрисами. Задача
ЗадачаВ ABC угол C равен 58°, AD и BE — биссектрисы,
пересекающиеся в точке O. Найдите угол AOB.
Сумма углов треугольника равна 180
А + В + С = 180
2 + 2 + 58 = 180
2 + 2 = 122
+ = 61
?
Из треугольника АОВ
АОВ = 180 - ( + )
АОВ = 180 – 61
АОВ = 119
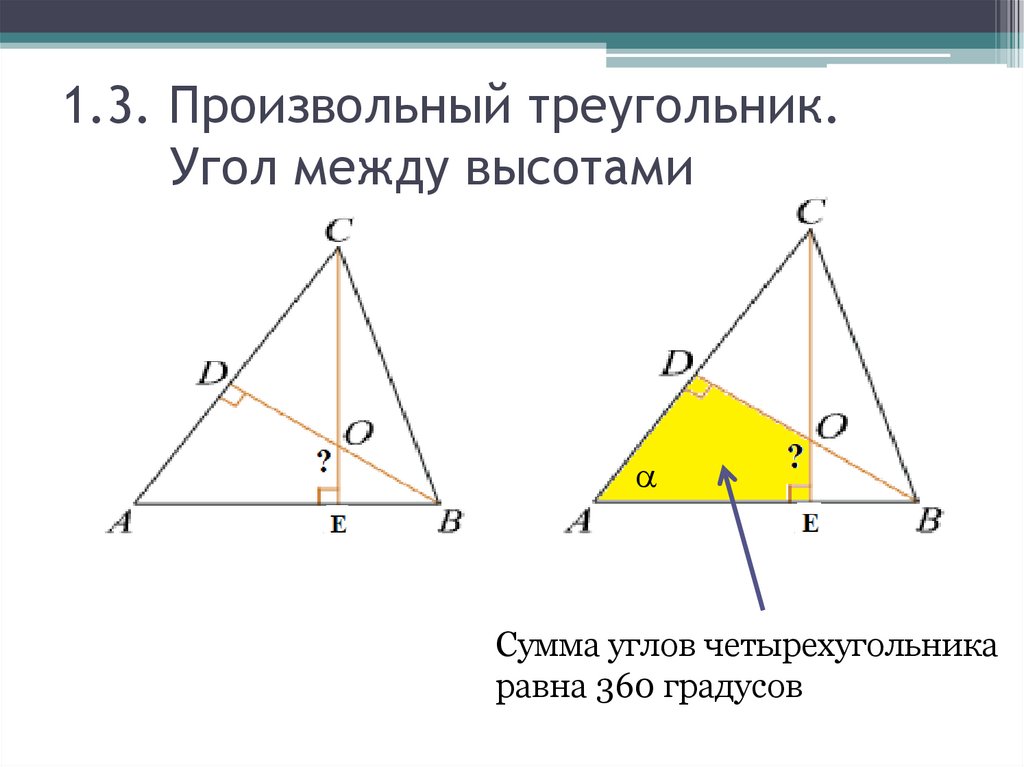
30. 1.3. Произвольный треугольник. Угол между высотами
Сумма углов четырехугольникаравна 360 градусов
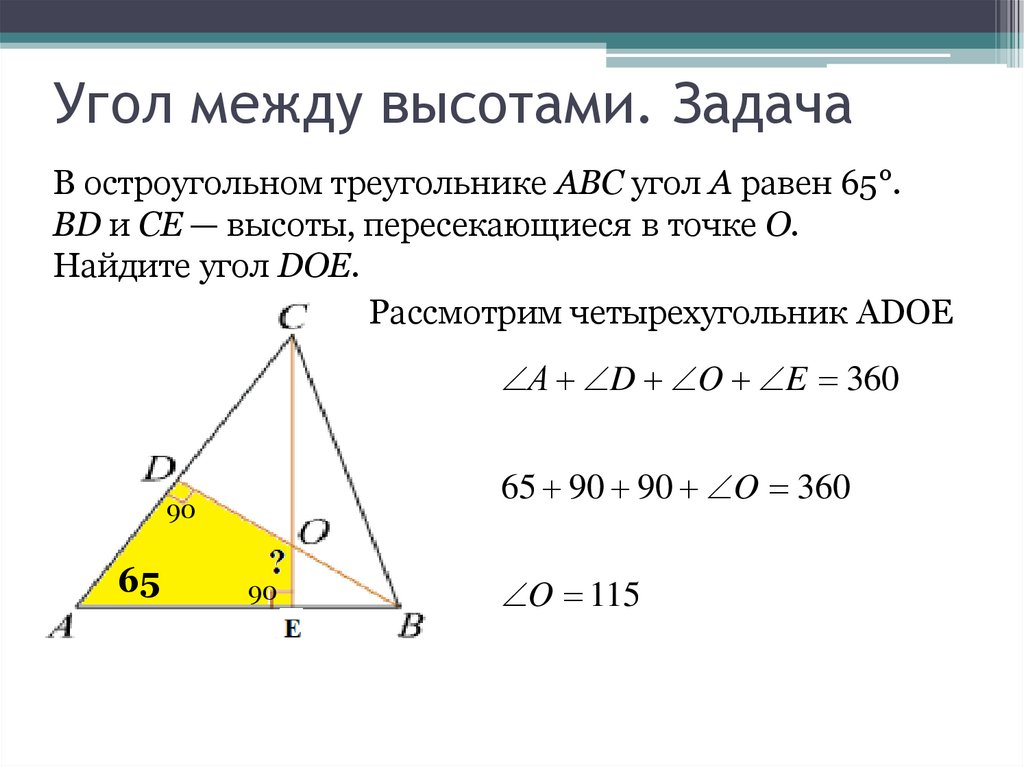
31. Угол между высотами. Задача
В остроугольном треугольнике ABC угол A равен 65°.BD и CE — высоты, пересекающиеся в точке O.
Найдите угол DOE.
Рассмотрим четырехугольник ADOE
А D O E 360
65 90 90 O 360
90
65
90
O 115
32. Угол между высотами. Задача
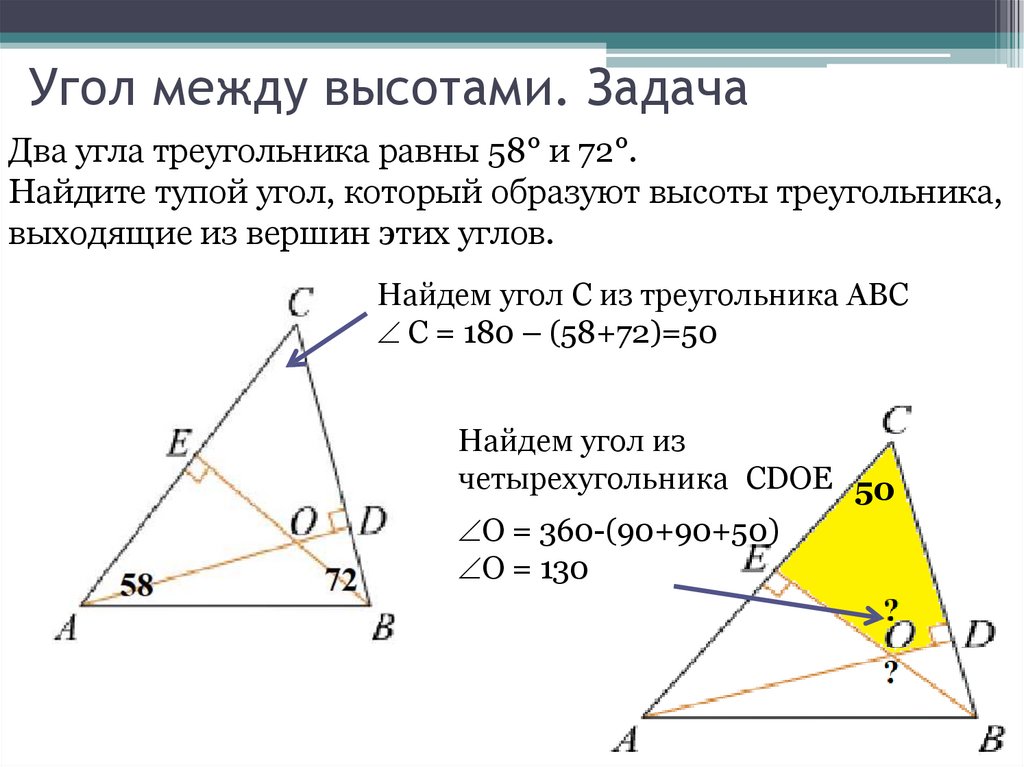
Два угла треугольника равны 58° и 72°.Найдите тупой угол, который образуют высоты треугольника,
выходящие из вершин этих углов.
Найдем угол С из треугольника АВС
С = 180 – (58+72)=50
Найдем угол из
четырехугольника CDOE 50
O = 360-(90+90+50)
O = 130
33. РЕШЕНИЕ ЗАДАЧ ИЗ ЕГЭ -26
ТРЕУГОЛЬНИКИ34.
35.
36.
37.
38.
39. ДОМАШНЯЯ РАБОТА
40.
41.
42.
43.
44. БЛАГОДАРЮ ЗА ВНИМАНИЕ!
УРОК ЗАКОНЧЕНБЛАГОДАРЮ ЗА ВНИМАНИЕ!














 mathematics
mathematics