_4.8.Свойства и графики функций

1.

Математику изучать надобно,
поскольку она в порядок ум приводит.
М.В Ломоносов

2. 2025 – 2026 учебный год

Дисциплина
ОУП.13
«Математика»
углубленный уровень
1 курс специальность
31.02.01 Лечебное дело

3. Домашнее задание

1. Специальные тригонометрические
формулы
2. Вычислить tg2250

4. Теоретическое занятие

Раздел 4. Основы тригонометрии. Тригонометрические функции
(30 час.)
Тема 4.8
Свойства и графики функций
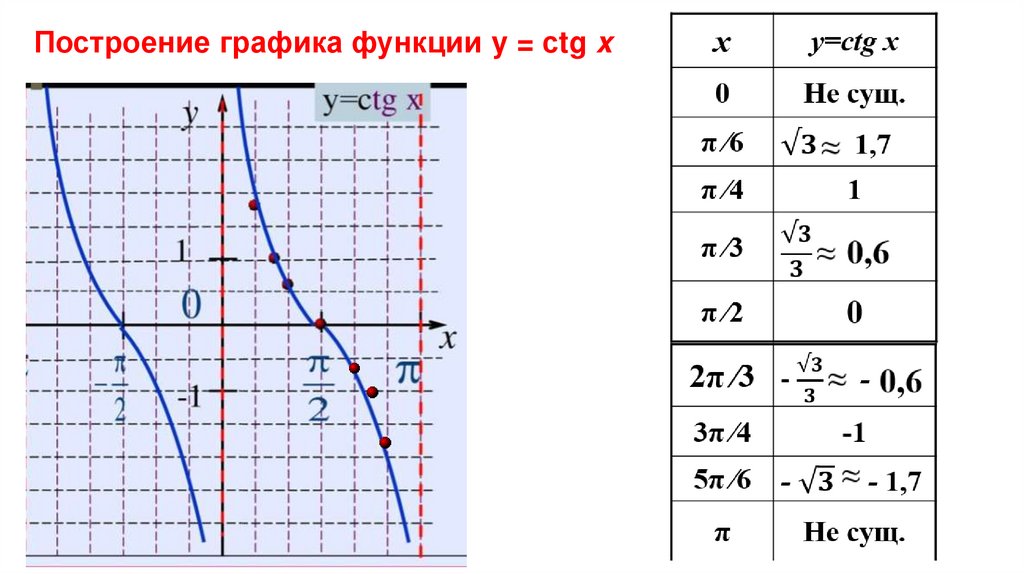
y = cos x, y = sin x, y = tg x, y = сtg x

5. Учебные вопросы

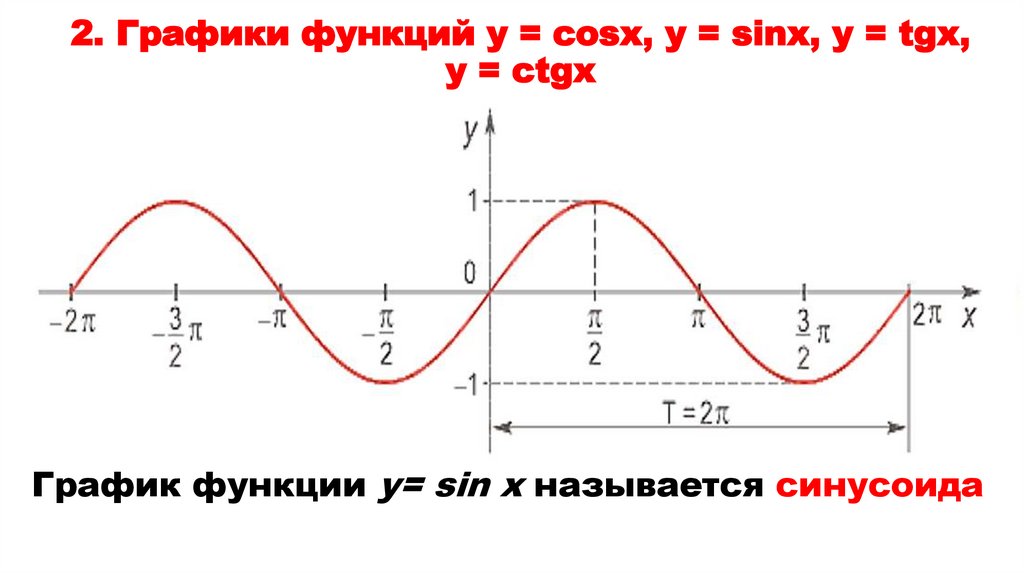
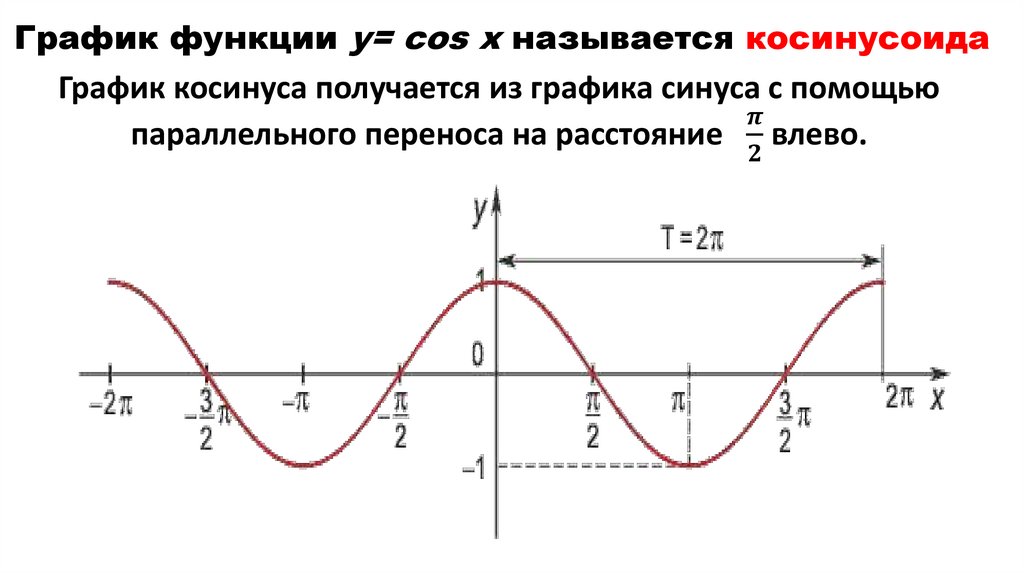
1. Основные свойства функций.
2. Графики функций
y = cos x, y = sin x, y = tg x, y = сtg x.
3. Свойства функций y = cos x, y = sin x,
y = tg x, y = сtg x.

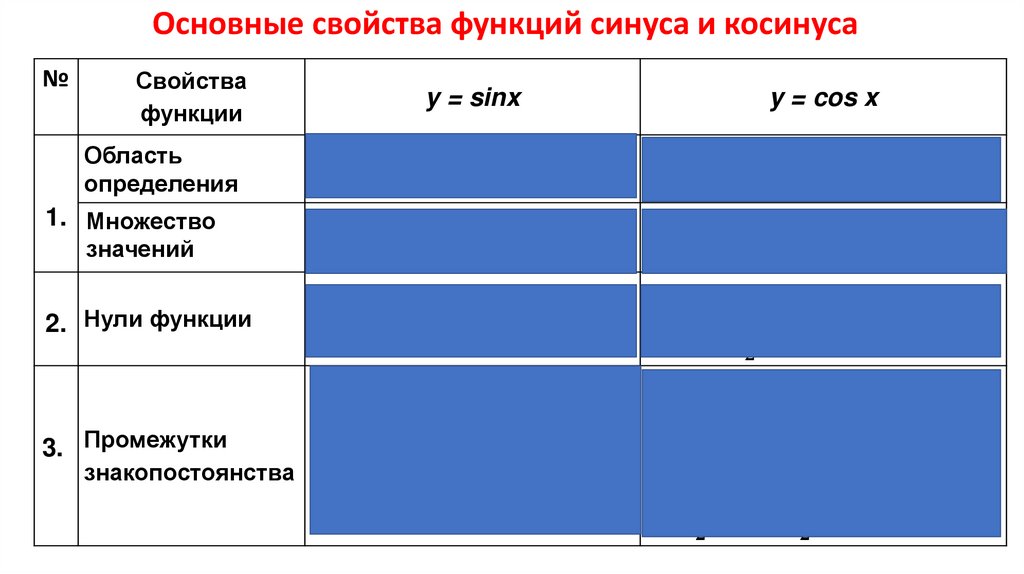
6. 1.Основные свойства функций

1) Область определения и область значений
2) Нули функции
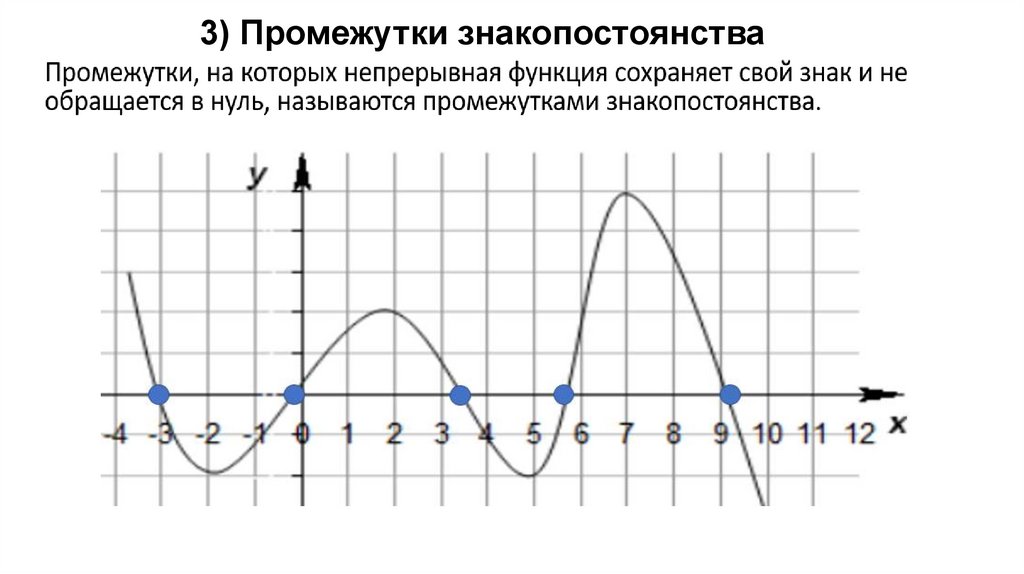
3) Промежутки знакопостоянства
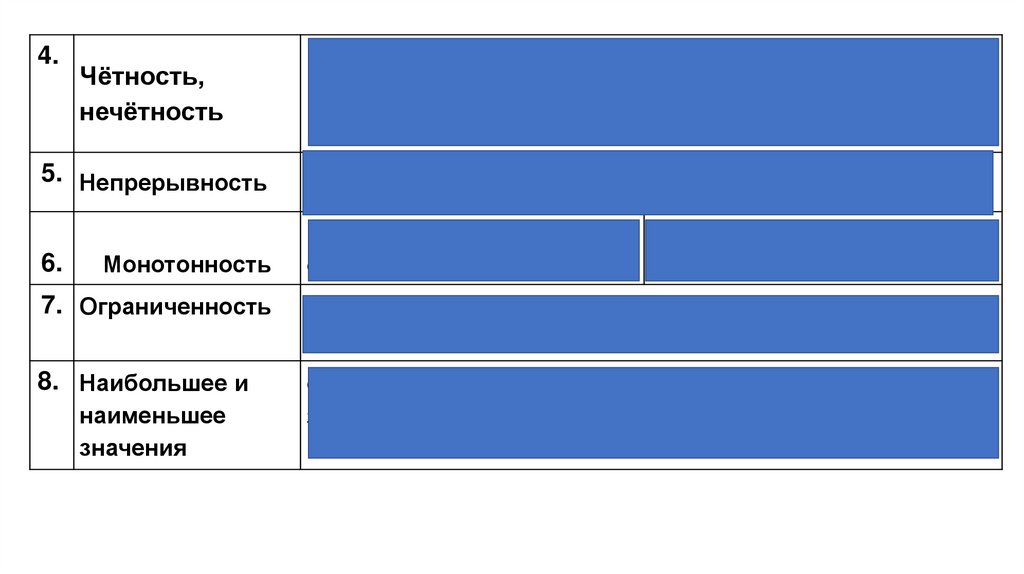
4) Четность
5) Непрерывность
6) Монотонность
7) Ограниченность
8) Наибольшее и наименьшее значения
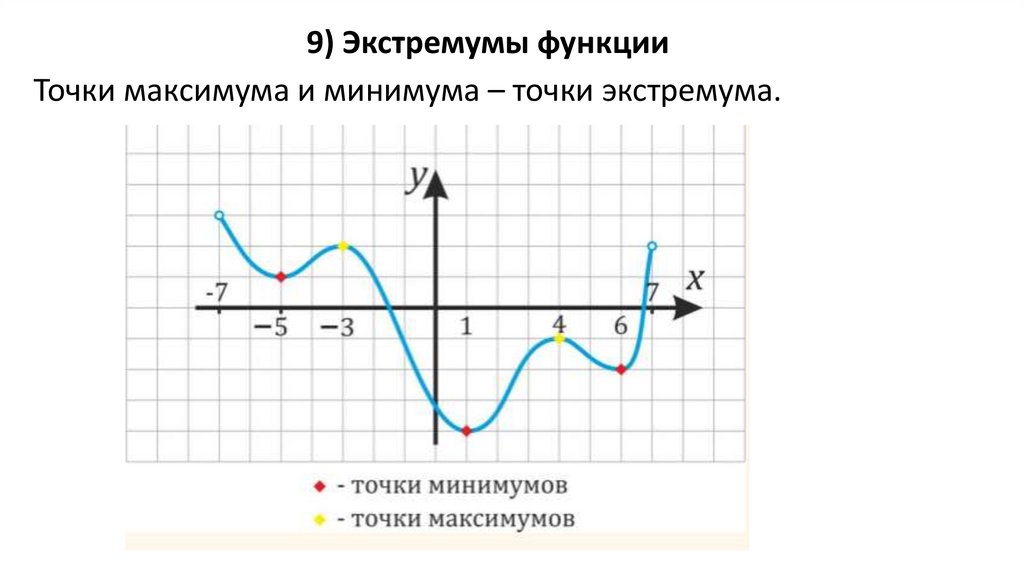
9) Экстремумы функции
10) Выпуклость, вогнутость функции
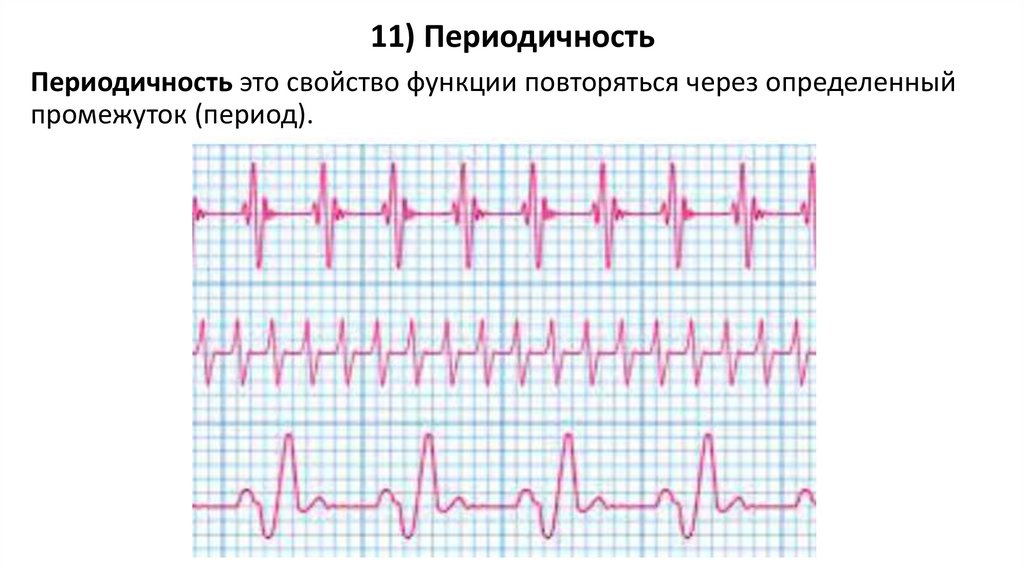
11) Периодичность

7. Область определения и область значений функций

1) Область определения и область значений функций
Определение. Областью определения функции
понимают все значения независимой переменной х, при
которых данная выражение f(x) имеет смысл). D(f) или
D(y).
Определение. Множеством значений функции
называются все значения зависимой переменной у. Е(f)
или Е(y).

8.

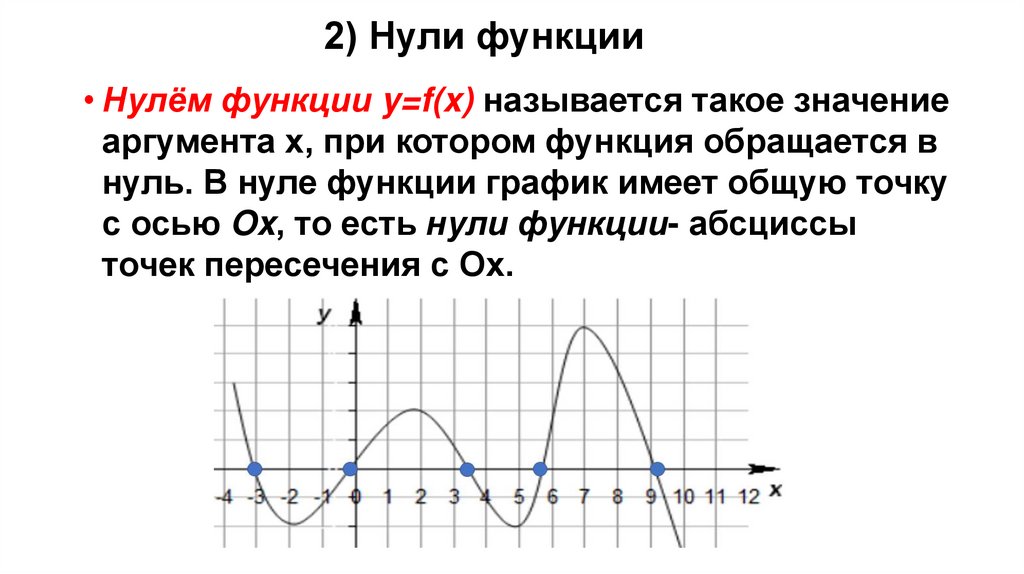
2) Нули функции
• Нулём функции y=f(x) называется такое значение
аргумента x, при котором функция обращается в
нуль. В нуле функции график имеет общую точку
с осью Ox, то есть нули функции- абсциссы
точек пересечения с Ох.

9.

3) Промежутки знакопостоянства

10.

4) Четность
Определение. Числовая функция f называется чётной,
если при всех значениях х из области определения этой
функции при изменении знака аргумента на
противоположный значение функции не изменяется, то
есть выполняется равенство f(-x)= f(x).
y
1
0 1
x
(График чётной функции симметричен относительно оси Оу )
Числовая функция f называется нечётной, если при
всех значениях х из области определения этой функции
при изменении знака аргумента на противоположный
функция изменяется только по знаку, то есть
выполняется равенство f(-x) = - f(x). (График нечетной
функции симметричен относительно начала координат)
y
1
0 1
x

11.

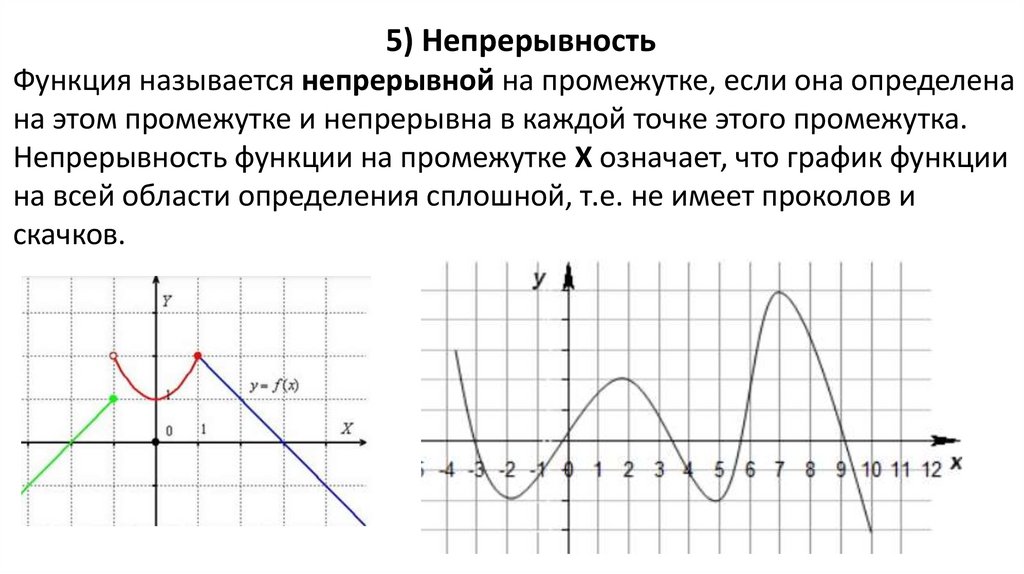
5) Непрерывность
Функция называется непрерывной на промежутке, если она определена
на этом промежутке и непрерывна в каждой точке этого промежутка.
Непрерывность функции на промежутке Х означает, что график функции
на всей области определения сплошной, т.е. не имеет проколов и
скачков.

12.

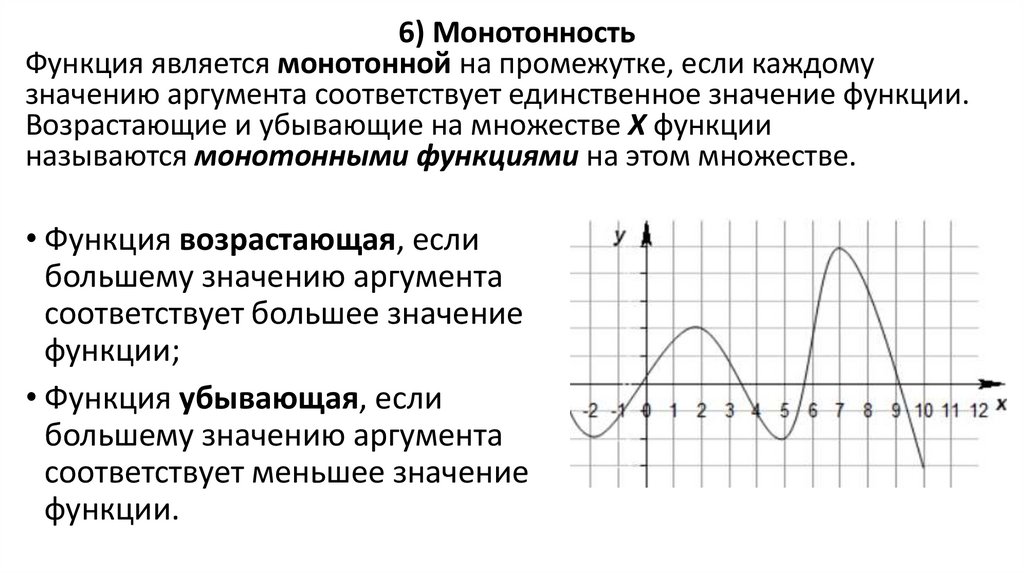
6) Монотонность
Функция является монотонной на промежутке, если каждому
значению аргумента соответствует единственное значение функции.
Возрастающие и убывающие на множестве Х функции
называются монотонными функциями на этом множестве.
• Функция возрастающая, если
большему значению аргумента
соответствует большее значение
функции;
• Функция убывающая, если
большему значению аргумента
соответствует меньшее значение
функции.

13.

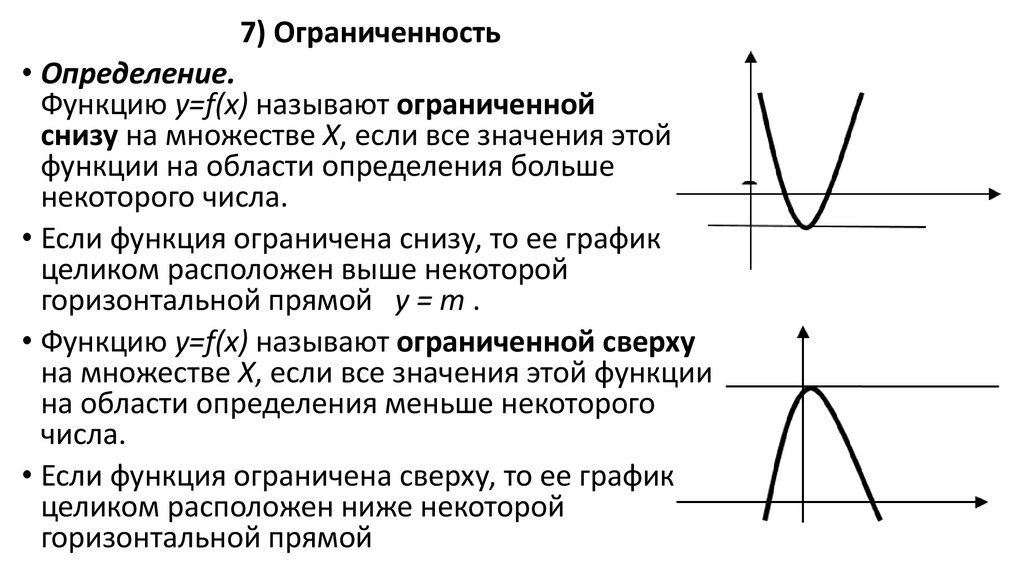
7) Ограниченность
• Определение.
Функцию y=f(x) называют ограниченной
снизу на множестве Х, если все значения этой
функции на области определения больше
некоторого числа.
• Если функция ограничена снизу, то ее график
целиком расположен выше некоторой
горизонтальной прямой у = m .
• Функцию y=f(x) называют ограниченной сверху
на множестве Х, если все значения этой функции
на области определения меньше некоторого
числа.
• Если функция ограничена сверху, то ее график
целиком расположен ниже некоторой
горизонтальной прямой

14.

8) Наибольшее и наименьшее значения
Определение. Число M называют наибольшим значением
функции y=f(x) на множестве D(f), если:
1) существует точка