Similar presentations:
4a4214a06e324b6a8995ff4f849e3fbd
1.
Обратныетригонометрические
функции
2.
Функция у = sin xу
1
0
2
-1
2
х
3.
4.
Функция y = arcsin xПо определению арксинуса числа для
каждого x∈[−1;1] определено одно число
y = arcsin x.
Тем самым на отрезке [−1;1] задана
функция y = arcsin x, −1 ≤ x ≤ 1.
Поэтому свойства функции y = arcsin x можно
получить из свойств функции y = sin x.
5.
Свойства функции y = arcsin x6.
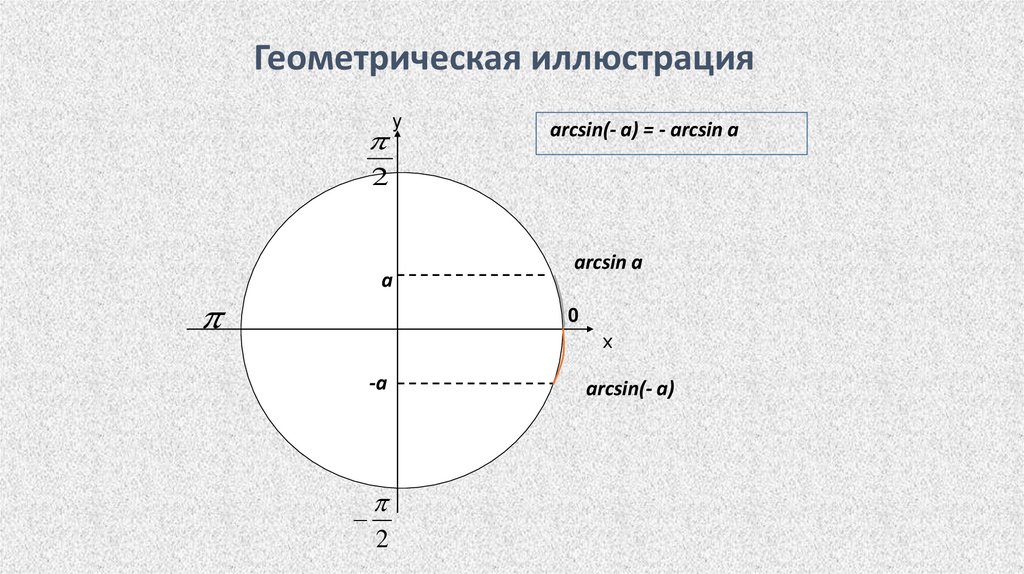
Геометрическая иллюстрацияу
arcsin(- a) = - arcsin a
2
a
arcsin a
0
х
-a
2
arcsin(- a)
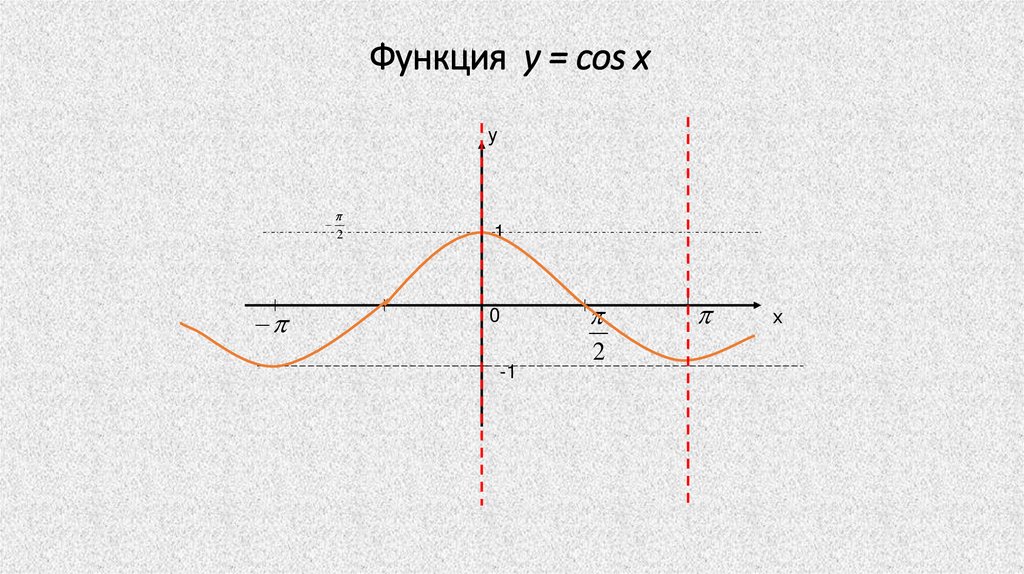
7. Функция у = cos x
у2
1
0
-1
2
х
8.
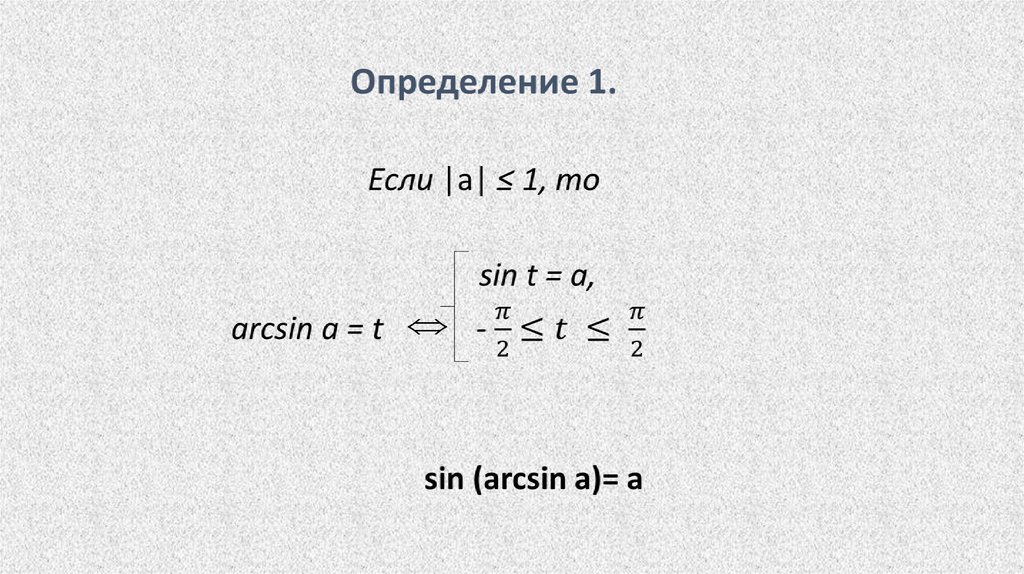
Определение 2.Если |a| ≤ 1, то
cos t = a,
arccos a = t
0 ≤ t ≤ π;
cos (arccos a)= a
9.
Функция y = arccos xПо определению арккосинуса числа для
каждого x∈[−1;1] определено одно число
y = arccos x.
Тем самым на отрезке [−1;1] задана
функция y = arccos x, −1 ≤ x ≤ 1.
Функция y = arccos x является обратной к
функции y = cos x, где 0 ≤ x ≤ π
Поэтому свойства функции y = arccos x можно
получить из свойств функции y = sin x.
График функции y = arccos x симметричен
графику функции y = cos x, где 0 ≤ x ≤ π,
относительно прямой y=x.
10.
Свойства функции y = arccos x1. Область определения — отрезок [−1;1]
2. Множество значений — отрезок [0; π]
3. Функция y = arccos x — убывает
4. Функция общего вида
11.
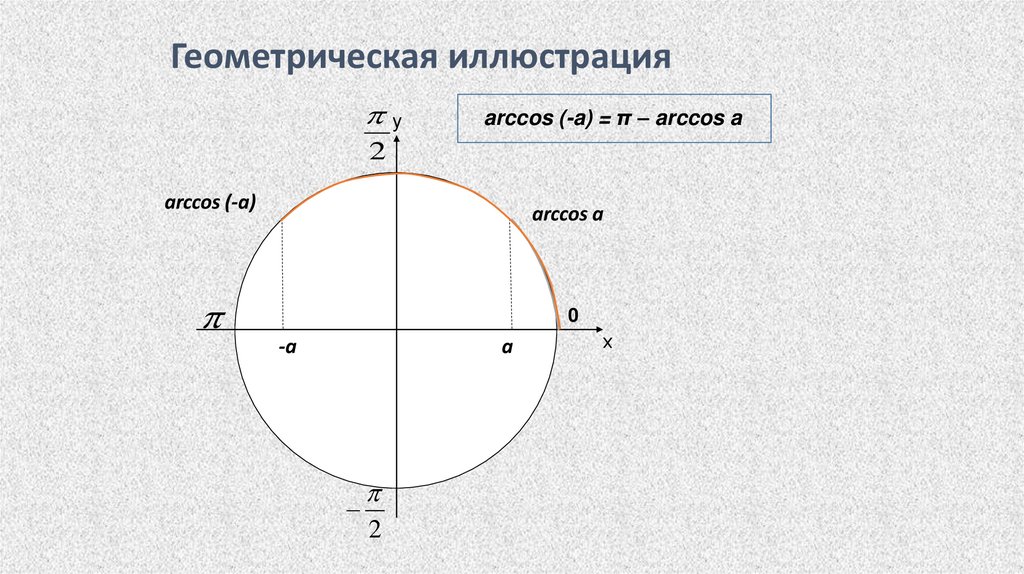
Геометрическая иллюстрацияу
arccos (-a) = π – arccos a
2
arccos (-a)
arccos a
0
-a
a
2
х
12.
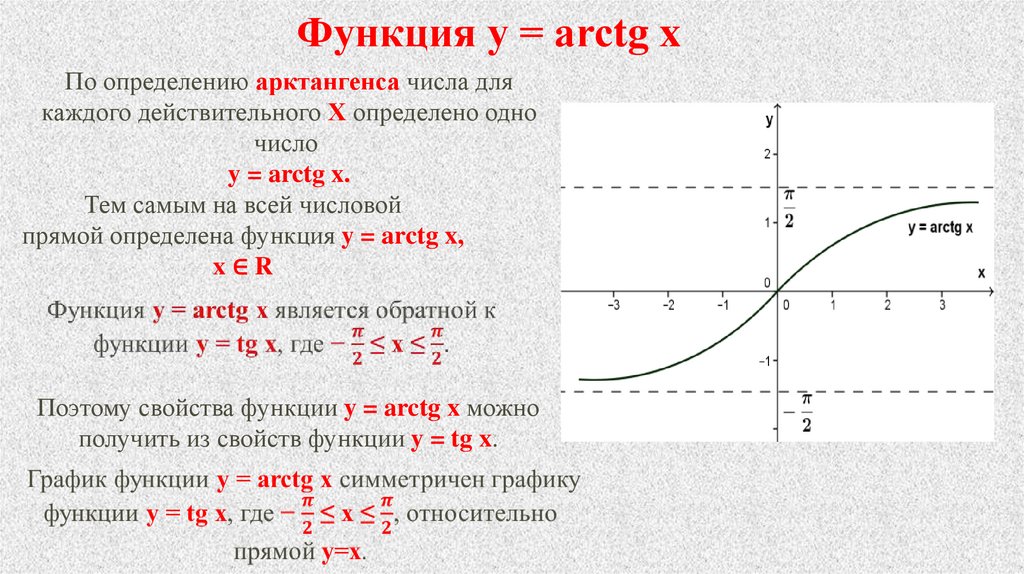
Функция y = arctg xПо определению арктангенса числа для
каждого действительного Х определено одно
число
y = arctg x.
Тем самым на всей числовой
прямой определена функция y = arctg x,
x∈R
Поэтому свойства функции y = arctg x можно
получить из свойств функции y = tg x.
13.
Свойства функции y = arctg x14.
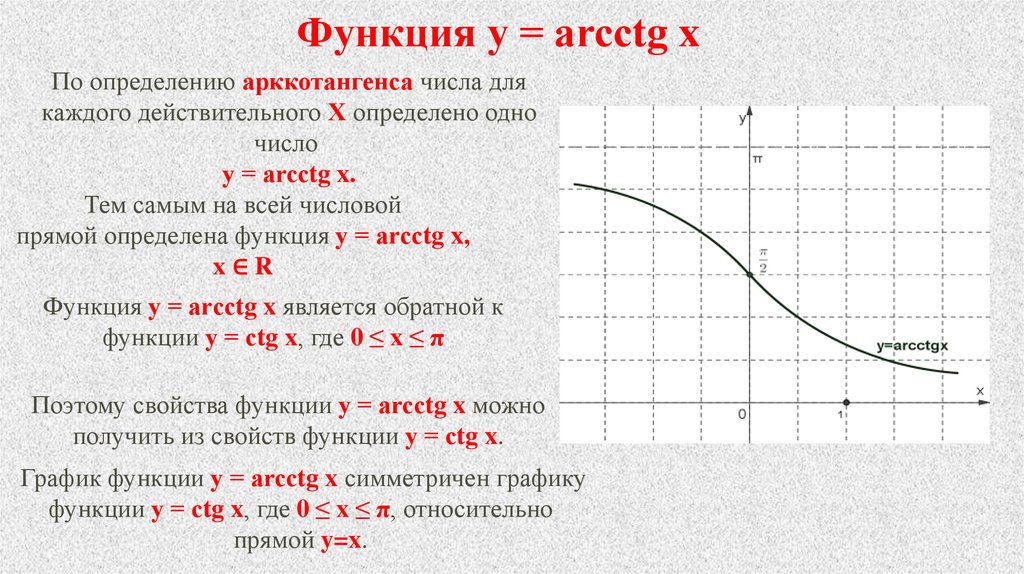
Функция y = arcсtg xПо определению арккотангенса числа для
каждого действительного Х определено одно
число
y = arcсtg x.
Тем самым на всей числовой
прямой определена функция y = arсctg x,
x∈R
Функция y = arсctg x является обратной к
функции y = сtg x, где 0 ≤ x ≤ π
Поэтому свойства функции y = arcсtg x можно
получить из свойств функции y = сtg x.
График функции y = arcсtg x симметричен графику
функции y = сtg x, где 0 ≤ x ≤ π, относительно
прямой y=x.
15.
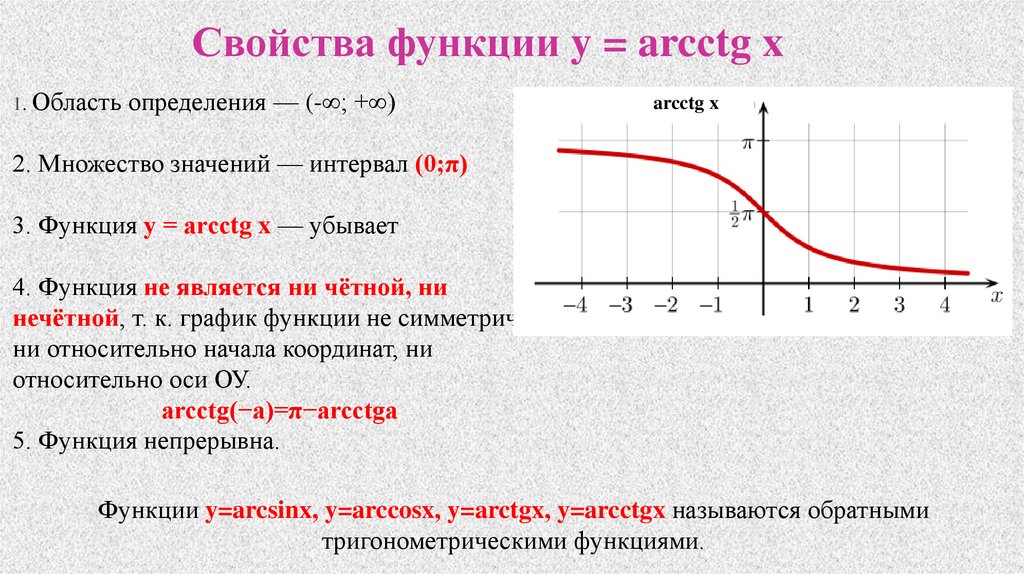
Свойства функции y = arcсtg x1. Область определения — (-∞; +∞)
arcctg x
2. Множество значений — интервал (0;π)
3. Функция y = arcсtg x — убывает
4. Функция не является ни чётной, ни
нечётной, т. к. график функции не симметричен
ни относительно начала координат, ни
относительно оси ОУ.
arcctg(−a)=π−arcctga
5. Функция непрерывна.
Функции y=arcsinx, y=arccosx, y=arctgx, y=arcctgx называются обратными
тригонометрическими функциями.
16.
Решение задачЗадача №1 Вычислить
Решение
17.
Задача №2 ВычислитьРешение

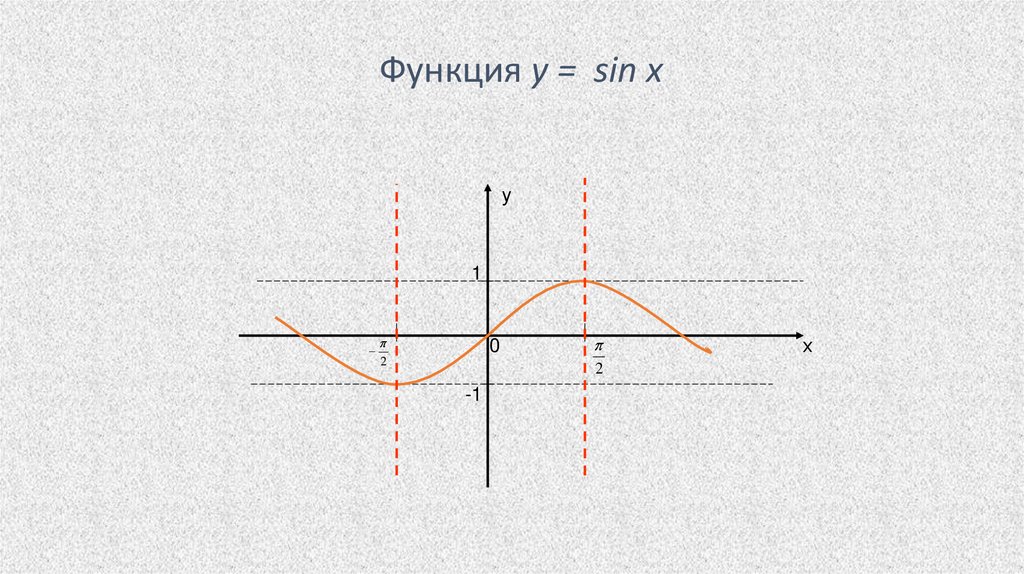








 mathematics
mathematics








