1285501

1. Комплексные числа

Комплексны
е числа

2. Содержание

• Понятие комплексного числа
• Операции над комплексными числами в
алгебраической форме
• Тригонометрическая и показательная формы
• Возведение комплексных чисел в степень

3. Понятие комплексного числа

• Z=a+bi – общая форма комплексного числа
• а, b – действительные числа
• i – мнимая единица

4. Понятие комплексного числа

а+bi - единое число!

5. Понятие комплексного числа

Джероламо Кардано
(1501-1576)
Поставил вопрос о
существовании
комплексных чисел

6. Понятие комплексного числа

Иоганн Карл
Фридрих Гаусс
(1777-1855)
Ввел понятие
«комплексное
число»

7. Понятие комплексного числа

Уильям Роуэн
Гамильтон
(1805-1865)
Предложил стандартную
модель комплексных чисел

8. Понятие комплексного числа

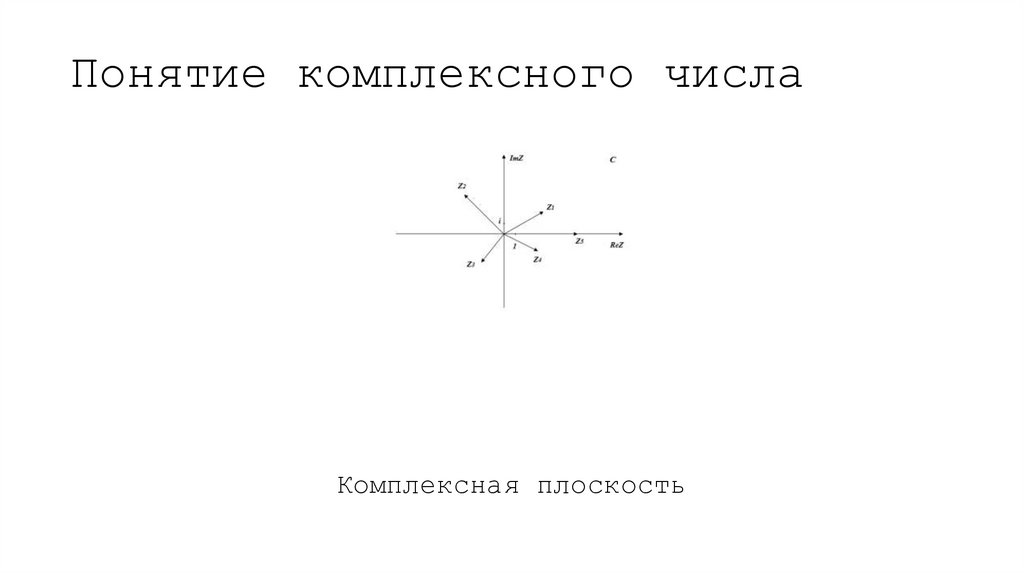
Комплексная плоскость

9. Понятие комплексного числа

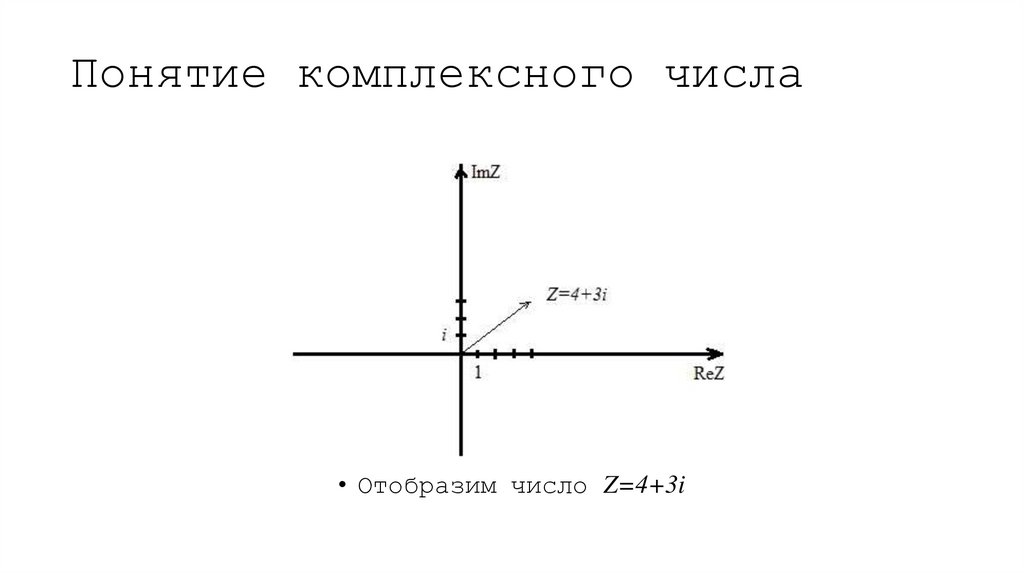
• Отобразим число Z=4+3i

10. Понятие комплексного числа

• Множество действительных чисел R
представляет собой подмножество
множества комплексных чисел С
R C

11. Понятие комплексного числа

Три формы комплексного числа:
• алгебраическая;
• тригонометрическая;
• показательная.

12. Операции над комплексными числами

Операции над комплексными числами в
алгебраической форме:
• сложение;
• вычитание;
• умножение;
• деление.

13. Операции над комплексными числами

• Сложение:
Действительные и мнимые числа складываются
отдельно

14. Операции над комплексными числами

• Вычитание:
• Действительные и мнимые числа
вычитаются отдельно

15. Операции над комплексными числами

• Умножение:
• Умножение осуществляется по правилам
умножения многочленов;
• Квадрат мнимой единицы равен -1
i 1
2

16. Операции над комплексными числами

• Умножение:

17. Операции над комплексными числами

• Деление:
• Умножение числителя и знаменателя на сопряженное
знаменателю выражение

18. Операции над комплексными числами

• Перевод в алгебраическую форму:

19. Тригонометрическая и показательная формы

• Любое, кроме нуля, комплексное
число Z=a=bi можно записать в
тригонометрической форме:
Z Z Cos iSin

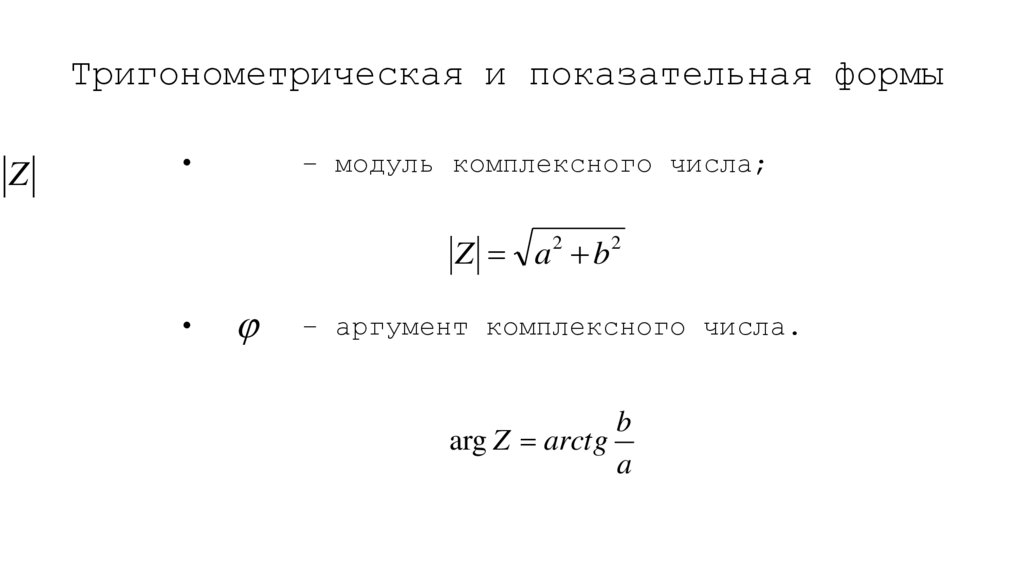
20. Тригонометрическая и показательная формы

Z
– модуль комплексного числа;
Z a 2 b2
– аргумент комплексного числа.
b
arg Z arctg
a

21. Тригонометрическая и показательная формы

Z 4 3i

22. Тригонометрическая и показательная формы

Формулы аргумента:
• a > 0 (I и IV четверти)
b
arg Z arctg
a
• a < 0, b > 0 (II
четверть)
b
arg Z arctg
a
• a < 0, b < 0 (III
четверть)
b
arg Z arctg
a

23. Тригонометрическая и показательная формы

• Комплексное число в показательной
форме имеет вид:
Z Ze
i

24. Тригонометрическая и показательная формы

Z 1 3i

25. Тригонометрическая и показательная формы

• Умножение комплексных чисел в
тригонометрической и показательной
форме:
• Модули перемножаем
• Аргументы складываем

26. Тригонометрическая и показательная формы

27. Тригонометрическая и показательная формы

• Деление в тригонометрической и показательной
форме:
• Модули делим
• Аргументы вычитаем

28. Возведение комплексных чисел в степень

• Формула Муавра:
Z Z Cos( n) iSin ( n)
n
n
Z Z e
n
n
i n

29. Возведение комплексных чисел в степень

• Абрахам де Муавр
(1667-1754)

30. Возведение комплексных чисел в степень

31. Возведение комплексных чисел в степень

• При возведении в степень
комплексного числа в алгебраической
форме необходимо помнить, что
i 1,
2
i 3 i ,
i 1
4
.........

32. Возведение в степень комплексного числа

n
Z
n
2 k
2 k
Z Cos
iSin
n
n
n
Z n Ze
2 k
n
k 0,1,..., (n 1).