Similar presentations:
Комплексные числа
1.
КомплексныеКомплексные числа.
числа.
Панарад А.Ю.
Кафедра Алгебры, Геометрии и Анализа.
ДВФУ
2.
ПЛАН:1. Основные понятия. Формы записи.
2. Действия над комплексными числами:
a)Сложение комплексных чисел;
b)Вычитание комплексных чисел;
c)Умножение комплексных чисел;
d)Деление комплексных чисел ;
e)Возведение в n-степень;
f)Извлечение корней из комплексных
чисел.
3.
Основные понятия.Определение.
Комплексным числом называется
выражение вида
,
z i
где и - действительные числа, а i - мнимая
единица, и
2
i 1
Например, = 6 i или = 1-5i .
Число называется действительной частью
комплексного числа и обозначается Re z,
а мнимой частью и обозначается Im
z.
4.
Основные понятия.Два комплексных числа
называются равными
тогда и только тогда,
когда равны их
действительные и
мнимые части.
Два комплексных числа,
отличающихся лишь
знаком мнимой части,
называются комплексносопряженными.
z1 1 1i ;
z 2 2 2i
z1 z 2 1 2 ; 1 2
z1 1 1i
z2 2 2i
5.
Примеры.Пример 1.
z1 5 3i ;
Пример 2.
z 2 25 / 5 15 / 5i
z 2 5 3i
5 25 / 5
3 15 / 5
Вывод : z1 z 2
z1 5 3i ;
Вывод : z1 и z 2
комплексно сопряженные числа.
6.
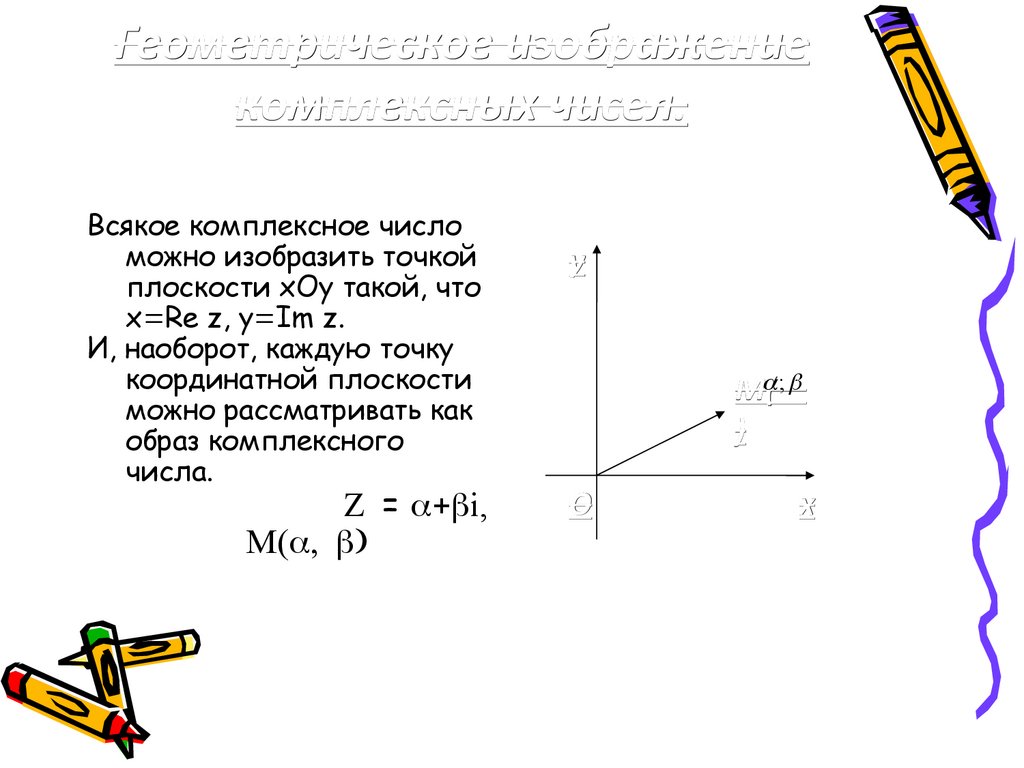
Геометрическое изображениекомплексных чисел.
Всякое комплексное число
можно изобразить точкой
плоскости xOy такой, что
x Re z, y Im z.
И, наоборот, каждую точку
координатной плоскости
можно рассматривать как
образ комплексного
числа.
= i,
М(
y
M( ;
)
O
x
7.
Геометрическое изображениекомплексных чисел.
y
M(x;y
)
O
x
Плоскость, на которой
изображается
комплексные числа,
называется комплексной
плоскостью.
Ось абсцисс Ox называется
действительной осью.
Ось ординат Oy называется
мнимой осью.
8.
Геометрическое изображениекомплексных чисел.
y
r OM
M(x;y)
φ
O
x
Комплексное число можно
задавать с помощью
радиус
вектора r OM .
Длина вектора называется
модулем этого числа и
обозначается ф фили r .
Величина угла между
положительным направлением
оси Ox и вектором r
называется аргументом этого
комплексного числа и
обозначается Arg или
Аргумент комплексного числа
определяется с точностью до
слагаемого
9.
Формы записикомплексных чисел.
1.Алгебраическая.
1.Алгебраическая.
2.Тригонометрическая.
2.Тригонометрическая.
3. Показательная.
Любое комплексное число можно
записать в любой форме.
10.
Формы записикомплексных чисел.
Модуль r и аргумент можно
рассматривать как полярные
координаты вектора r OM
Тогда получаем x r cos
y r sin
Комплексное число z= i
можно записать в виде
z r cos ir sin
Или
z r (cos i sin )
Запись числa
z= i
называется
алгебраической формой
комплексного числа.
Запись числа z в виде
z=r(cosφ+isinφ)
называется
тригонометрической
формой
комплексного числа.
11.
Переход от одной формы к другой.От алгебраической формы к
тригонометрической
r z x2 y2
x
y
cos
sin
r
r
y
Т.к.
x
То Arg z arg z 2 k
tg
cos cos(arg z 2 k )
sin sin(arg z )
От тригонометрической
формы к
алгебраической
x r cos
y r sin
12.
При переходе от алгебраической формыкомплексного числа к тригонометрической
достаточно определить главное значение
аргумента, т.е. arg z
Т.к.
то
arg z
arctg
arg z arctg
arctg
y
tg
x
y
для точек I и IV четвертей;
x
y
для точек II четверти;
x
y
для точек III четверти.
x
13.
Пример: Комплексное числоизобразить на плоскости и записать в
тригонометрической форме z 2 2i
x 2
y 2
y
2
φ
0
r z x2 y2
2
x
r 2 2 2 2 2 2
Для I четверти
y
2
arg z arctg arctg arctg1
x
2
arg z
4
2 2i 2 2 (cos i sin )
4
4
14.
Комплексное число можно записатьв показательной
(или экспонентной) форме
z re
i
arg z
Где r z и
i
e
cos i sin
В силу формулы Эйлера
i
функция e периодическая с основным периодом 2π.
Для записи комплексного числа в показательной
форме надо определить главное значение
аргумента и модуль.
15.
2. Действия надкомплексными числами
Суммой двух комплексных
чисел
z1 x1 y1i
z 2 x2 y 2 i
Называется комплексное
число
z1 z 2 ( x1 x2 ) ( y1 y2 )i
Разностью двух комплексных
чисел z1 x1 y1i
z 2 x2 y 2 i
Называется комплексное
число
z1 z2 ( x1 x2 ) ( y1 y2 )i
Геометрически комплексные
числа складываются и
вычитаются, как векторы.
16.
Сложение (вычитание)комплексных чисел
Примеры:
1. z1 4 2i
z 2 5 3i
z1 z 2 (4 5) (2 3)i 1 5i
2.
z1 3 5i
z 2 2 7i
z1 z 2 (3 2) ( 5 ( 7)i 1 2i
17.
Произведение и частноекомплексных чисел в
алгебраической форме.
Произведением двух
комплексных чисел
z1 x1 y1i
z 2 x2 y 2 i
называется комплексное
число
z z1 z 2 ( x1 x2 y1 y2 ) ( x1 y2 y1 x2 )i
Формула получается путем
перемножения двучленов!
( x1 y1i )( x2 y2i )
Частным двух комплексных
чисел
z1 x1 y1i
z 2 x2 y 2 i
называется комплексное
число
z
xx y y
yx xy
z 1 1 22 12 2 1 22 12 2 i
z2
x2 y 2
x2 y 2
На практике используют
умножение числителя и
знаменателя на число,
сопряженное
знаменателю! ( x y i)
( x2 y 2 i )
( x2 y 2 i ) ( x2 y 2 i )
1
1
18.
Произведение и частное комплексных чиселв алгебраической форме.
Частное:
Произведение:
z1 1 2i
z1 1 2i
z 2 3 4i
z 2 1 i
z1 z 2 (1 2i ) (3 4i )
1 2i (1 2i )(1 i )
1 i
(1 i )(1 i )
1 3 2i 3 1 4i 2i 4i
4 6i 4i 8i 2 4 10i 8
4 10i
1 2i i 2 3 i
1 1
2
z1 z 2 4 10i
2
i 1
z1 3 1
i
z2 2 2
19.
Произведение и частноекомплексных чисел в
тригонометрической форме.
Произведение чисел
z1 r1 (cos 1 i sin 1 )
z 2 r2 (cos 2 i sin 2 )
Находим по формуле
z1 z 2 r1r2 (cos( 1 2 ) i sin( 1 2 ))
При умножении модули
перемножаются, а
аргументы складываются!
Частное чисел
z1 r1 (cos 1 i sin 1 )
z 2 r2 (cos 2 i sin 2 )
Находим по формуле
z1 r1
(cos( 1 2 ) i sin( 1 2 ))
z 2 r2
При делении модули
делятся, а аргументы
вычитаются!
20.
Произведение и частное комплексных чиселв тригонометрической форме.
Произведение:
Частное:
i sin )
3
3
z 2 5(cos i sin )
z1 z2 3 5(cos( ) i sin( ))
3
3
z1 3(cos
z1 3(cos
4
4
z1 z 2 15(cos
i sin
)
3
3
i sin )
3
3
z2 5(cos i sin )
z1 3
(cos( ) i sin( ))
z2 5
3
3
z1 3
2
2
(cos(
) i sin(
))
z2 5
3
3
21.
Произведение и частноекомплексных чисел в
показательной форме.
z1 r1e
i 1
z 2 r2 e
i 2
z1 z 2 r1r2 e
i ( 1 2 )
z1 r1 i ( 1 2)
e
z 2 r2
z1 2e
i
2
i
3
z 2 3e
z1 z 2 6e
z1 2
e
z2 3
i
i
5
6
6
22.
Возведение комплексных чисел встепень.
Правило умножения комплексных чисел позволяет
возвести число в n-степень:
z n z z z ...
n
Получим Формулу Муавра:
z n r n (cos n i sin n )
Для показательной формы используют формулу:
z n r n e in
23.
Возведение комплексных чисел встепень.
Пример.
Найти (1 3i ) 9
Запишем число в тригонометрической форме:
r 1 3 2,
arg z arctg 3 ,
3
z 2(cos i sin )
3
3
z 9 (1 3i )9 29 (cos 9 i sin 9 )
3
3
29 (cos 3 sin 3 ) 29 ( 1) 512.
24.
Извлечение корней из комплексныхчисел в тригонометрической
форме.
Определение.
Корнем n-й степени из комплексного числа z называется
комплексное число ω, удовлетворяющее равенству:
n
z
n
Данное действие выполняется над комплексными
z
числами в тригонометрической форме.
2 k
2 k
n
r
(cos
i
sin
)
r
(cos
i
sin
)
Получим n различных корней!
n
n
n
25.
Извлечение корней из комплексныхчисел.
Пример.
6
Найти
z, если
z 1
В тригонометрической форме число имеет вид:
1 cos i sin
6
1 cos
2k
2k
i sin
6
6
Используем формулу:
Найдем 6 возможных корней, придавая k последовательно значения
0,1,2,3,4,5:
i sin i
2
2
3 1
k 0, z1 cos i sin
i
6
6
2 2
k 1, z 2 cos
5
5
3 1
k 2, z1 cos
i sin
i
6
6
2 2
3
3
k 4, z1 cos
i sin
i
2
2
k 3, z1 cos
7
7
3 1
i sin
i
6
6
2 2
k 5, z1 cos
11
11
3 1
i sin
i
6
6
2 2
























 mathematics
mathematics








