Similar presentations:
Комплексные числа
1.
Первое высшее техническое учебное заведение РоссииСанкт-Петербургский горный университет императрицы
Екатерины II
ЛЕКЦИЯ 6
Комплексные числа
24.05.2025
1|15
2.
Содержание лекции• Определение комплексного числа (к.ч.);
• Формы представления к.ч.;
• Свойства операций над к.ч.
2|15
3.
Комплексное число (к.ч.)z = x + iy, где x, y R,
i – символ мнимая единица, i 2 = − 1.
Множество всех к.ч. – С
x – вещественная часть к.ч. z
x = Re z
y — мнимая часть к.ч. z
y = Im z.
К.ч. , у которых мнимая часть Im z = 0 – чисто вещественные
К.ч., у которых вещественная часть Re z = 0 – чисто мнимые.
Число z = x - iy – комплексно-сопряженное числу z = x + iy.
Очевидно:
Re z = Re z , Im z = - Im z .
z = x + iy – алгебраическая форма к.ч.
3|15
R C.
4.
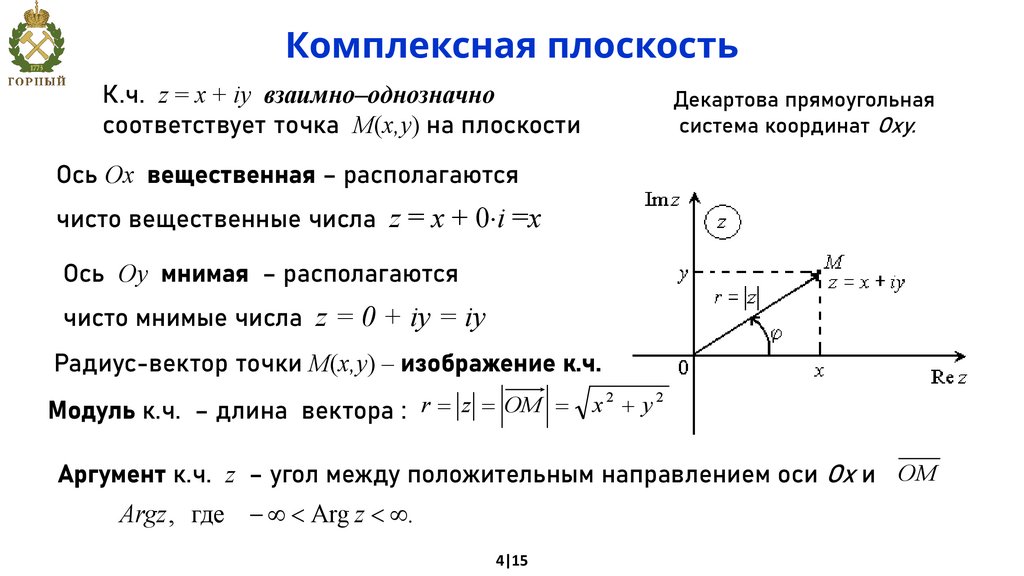
Комплексная плоскостьК.ч. z = x + iy взаимно–однозначно
соответствует точка M(x,y) на плоскости
Декартова прямоугольная
система координат Oxy.
Ось Ox вещественная – располагаются
чисто вещественные числа z = x + 0 i =x
у
Ось Oy мнимая – располагаются
чисто мнимые числа z = 0 + iy = iy
Радиус-вектор точки M(x,y) – изображение к.ч.
Модуль к.ч. – длина вектора : r = z = OM =
x2 + y2
Аргумент к.ч. z – угол между положительным направлением оси Ox и OM
Argz , где - ¥ < Arg z < ¥.
4|15
5.
Наименьшее по модулю значение аргумента– главное значение: arg z =
Arg z = arg z + 2pk ,
- p < arg z £ p
Тригонометрическая
z = x + iy =
форма к.ч.
r cos j
r sin j
Действия с к.ч.
Два к.ч. z1 = x1 + iy1 ; z2 = x2 + iy2 равны
r (cos j + i sin j )
k Î Z.
y
= tgj
x
ì x1 = x2 ;
z1 = z 2 Û í
î y1 = y2 .
Сумма (разность) к.ч. - число вида:
z1 ± z 2 = (x1 + iy1 )± (x 2 + iy 2 ) = (x1 ± x 2 )+ (y1 ± y 2 ) i
5|15
6.
Произведение к.ч. – число вида: z1 z 2 = (x1 + y1i )× (x 2 + y 2 i ) == x1 x 2 + x1 y 2 i + x 2 y1i + y1 y 2 i 2 = (x1 x2 - y1 y2 )+ (x1 y2 + x2 y1 )i
Для комплексно-сопряженных чисел получим:
z + z = (x + iy )+ (x - iy )= 2 x = 2 Re z
z - z = (x + iy )- (x - iy ) = 2iy = 2i Im z
z × z = (x + iy )(x - iy ) = x - i y = x + y
2
2
2
2
2
Частное к.ч. – число вида:
(x1 + iy1 )(x2 - iy 2 )
z1
x1 + iy1
=
=
=
z 2 x 2 + iy 2 (x 2 + iy 2 )(x 2 - iy 2 )
x1 x 2 - ix1 y 2 + iy1 x 2 - i 2 y1 y 2
(
x1 x2 + y1 y2 ) + i (x2 y1 - x1 y2 )
=
=
x22 + y22
x 22 - i 2 y 22
z1
x1 x 2 + y1 y 2
x 2 y1 - x1 y 2
=
+i×
2
2
z2
x2 + y2
x 22 + y 22
6|15
7.
Свойства действий сложения и умножения1. z1 + z 2 = z 2 + z1 - коммутативность сложения.
2. (z1 + z 2 )+ z3 = z1 + (z 2 + z3 ) - ассоциативность сложения.
3. $0 = 0 + 0i : "z z + 0 = z - существование нулевого элемента.
4. "z $(- z ) : - z + z = 0 - существование противоположного элемента.
5. z1 × z2 = z2 × z1 - коммутативность умножения.
6. (z1 × z 2 )× z 3 = z1 × (z 2 × z 3 ) - ассоциативность умножения.
7. ( z1 + z 2 ) × z 3 = z1 × z 3 + z 2 × z 3 - дистрибутивность.
8. $ 1 : "z z × 1 = z - существование единицы.
9. "z ¹ 0 $z -1 : z × z -1 = 1 - существование обратного элемента.
7|15
8.
Пример. Для чисел z1 =2+i и z2 =3 –5iвычислить сумму, произведение и частное.
z1 + z 2 = (2 + i ) + (3 - 5i ) = (2 + 3) + (1 - 5)i = 5 - 4i
z1 × z 2 = (2 + i ) × (3 - 5i ) = (6 + 5) + (3 - 10)i = 11 - 7i
z1
(2 + i )
(2 + i ) (3 + 5i ) (6 - 5) + (3 + 10)i
=
=
×
=
2
2
z 2 (3 - 5i )
(3 - 5i ) (3 + 5i )
3 +5
1 13
=
+ i
34 34
8|15
9.
Действия с к.ч. в тригонометрической формеz = r (cos j + i sin j )
z1 × z 2 = (r1 (cos j1 + i sin j1 ))× (r2 (cos j 2 + i sin j 2 )) =
= r r (cos j cos j + i cos j sin j + i cos j sin j + i sin j sin j )=
1 2
1
2
1
2
2
1
2
1
2
= r1r2 ((cos j1 cos j 2 - sin j 2 sin j1 ) + i (cos j1 sin j 2 + cos j 2 sin j1 ))
sin (j1 +j 2 )
cos (j1 +j 2 )
= r1r2 (cos (j1 + j2 )+ i sin (j1 + j2 ))
z1 z2 = z1 z2
Arg (z1 z 2 ) = arg z1 + arg z 2 + 2pk
9|15
k ÎZ
10.
х= 312 ?
( 3 - i)
(
)
y = –1
r =| z |=
1
y
= tgj tgj = 3
x
2
3 + (-1) 2 = 2
p
j = arg z = 6
æ æ pö
æ p öö
3 - i = 2çç cosç - ÷ + i sin ç - ÷ ÷÷
è 6 øø
è è 6ø
æ 12p ö
æ 12p ö ö 212 (cos(- 2p )+ i sin (- 2p )) =
÷ + i sin ç ÷ ÷÷ =
3 - i = 2 çç cosç è 6 øø
è è 6 ø
12
12
= 2 (cos 0 + i sin 0 ) = 2
Комплексно-сопряженные
числа
z = x - iy = r cos - j + i sin - j
12
12 æ
(
( )
( ))
r (cos (- j)+ i sin (- j)) 1
1
z
=
=
= (cos (- j )+ i sin (- j ))
2
z z×z
r
r
z
2
2
z ×z = x + y = r
2
z1
1
1
= z1 ×
= r1 (cos j1 + i sin j1 )× (cos (- j 2 )+ i sin (- j 2 )) =
z2
z2
r2
r1
(cos (j1 - j 2 )+ i sin (j1 - j 2 ))
=
r2
10|15
z1
z1
=
z2
z2
æ z1 ö
Argçç ÷÷ = а rg z1 - а rg z 2 + 2pk , k Î Z
è z2 ø
11.
Корень из к.ч.Извлечь корень целой положительной степени n из к.ч z –
это найти такое к.ч. w = n z , чтобы выполнялось равенство w n = z.
Если
z = r (cos j + i sin j) , то найти w = r (cosy + i siny )
w = r (cos ny + i sin ny )= r (cos j + i sin j )
n
n
Из равенства двух к.ч.:
n
r =r Þ r= r
n
ny = j + 2pk , k Î Z Þ y =
формула Муавра:
n
j + 2pk
n
j + 2pk
j + 2pk ö
æ
z = r ç cos
+ i sin
÷, k = 0, 1, K, , n - 1
n
n ø
è
n
11|15
, kÎZ
12.
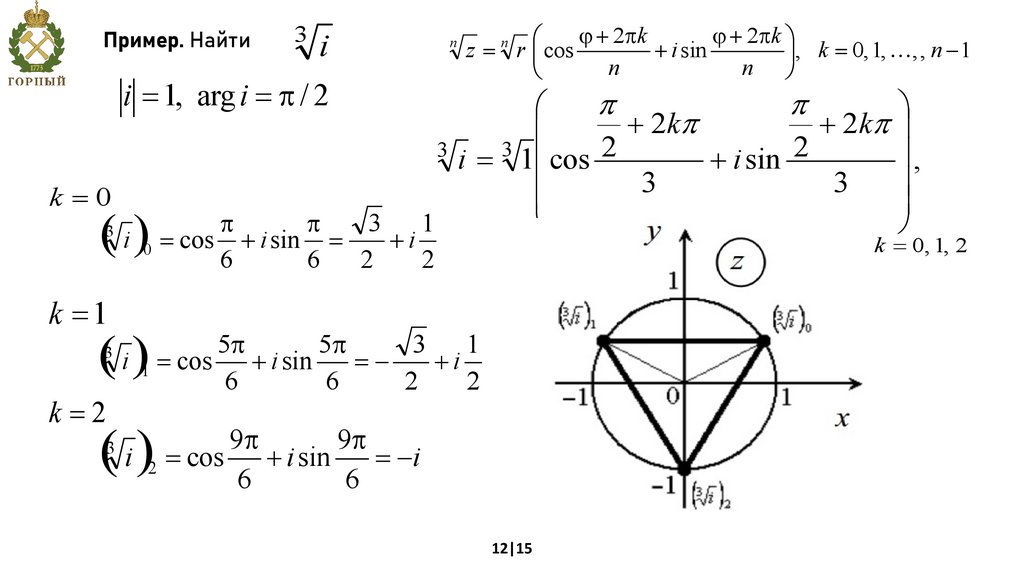
Пример. Найти3
i
i = 1, arg i = p / 2
k =0
()
3
k =1
n
j + 2pk
j + 2pk ö
æ
z = r ç cos
+ i sin
÷, k = 0, 1, K, , n - 1
n
n ø
è
n
p
p
æ
ö
+ 2kp
+ 2kp ÷
ç
3
÷,
i = 3 1ç cos 2
+ i sin 2
3
3
ç
÷
ç
÷
è
ø
1
p
p
3
i 0 = cos + i sin =
+i
6
6
2
2
k = 0, 1, 2
()
3
k =2
5p
5p
3
1
i 1 = cos
+ i sin
=+i
6
6
2
2
()
3
9p
9p
i 2 = cos + i sin
= -i
6
6
12|15
13.
Показательная форма к.ч.Формула Эйлера: e
ij
показательная форма к.ч. :
e
= cos j + i sin j
ip
i
p
= -1
e 2 =i
z = r (cos j + i sin j ) = re ,
ij
r = z , j = arg z.
где
Действия над к.ч. в показательной форме – обычные правила алгебры.
Пример: a = e
2+3i
a × (b ) = e
( ) = 25e
2
2+3i
=e e
1-i 2
× 5e
2 3i
1-i
b = 5e
2+3i
×e
= 5ee
2(1-i )
13|15
-1i
(
2+ 2 )+ (3- 2 )i = 25e 4+i = 25e 4 e i
= 25e
14.
Квадратные уравнения свещественными коэффициентами
2
az + bz + c = 0
2
- b ± b - 4ac
z1, 2 =
2a
Найти корни уравнения
2
z + 2z + 2 = 0
- 2 + 4 - 8 - 2 + 2 -1
z1, 2 =
=
= -1 ± i
2
2
14|15
-1 = ±i
15.
Спасибо за вниманиеСанкт-Петербургский горный
университет
императрицы Екатерины II,
199106, г. Санкт-Петербург,
Малый пр. В.О., д. 83
Тел.: +7(812) 328-82-98;
15|15






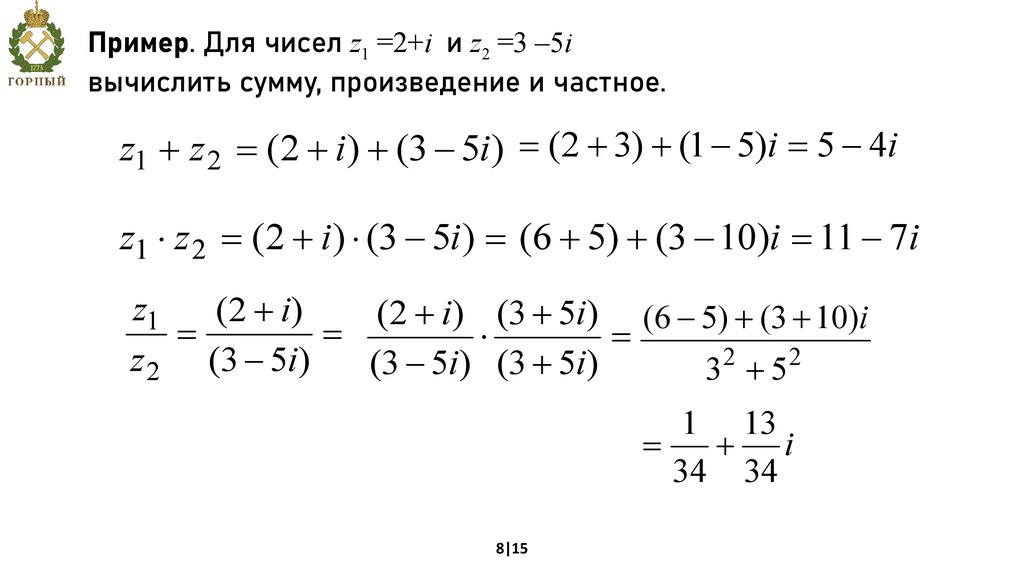






 mathematics
mathematics








