Similar presentations:
Определитель матрицы
1.
Определитель или детерминант– это число,
характеризующее квадратную
матрицу.
Обозначается:
a11 a12
a21 a22
A det A det( aij ) A
... ...
an1 an 2
... a1n
... a2 n
... ...
... ann
2.
Для определителей, как и для матриц,используются такие понятия, как строка,
столбец, диагональ и т.д.
Квадратная матрица, определитель
которой не равен нулю, называется
невырожденной.
Квадратная матрица, определитель
которой равен нулю, называется
вырожденной.
3.
Определителем первого порядкаматрицы
A (a11)
называется число
То есть:
A a11 a11
a11
4.
Определителем второго порядканазывается число, которое
определяется по правилу:
a11
a12
a21 a22
a11 a22 a12 a 21
5.
Определителем третьего порядканазывается число, которое
определяется по правилу:
a11 a12 a13
a21 a22 a23 a11 a22 a33 a12 a23 a31 a13 a21 a32
a31 a32 a33
a13 a22 a31 a12 a21 a33 a11 a23 a32
6.
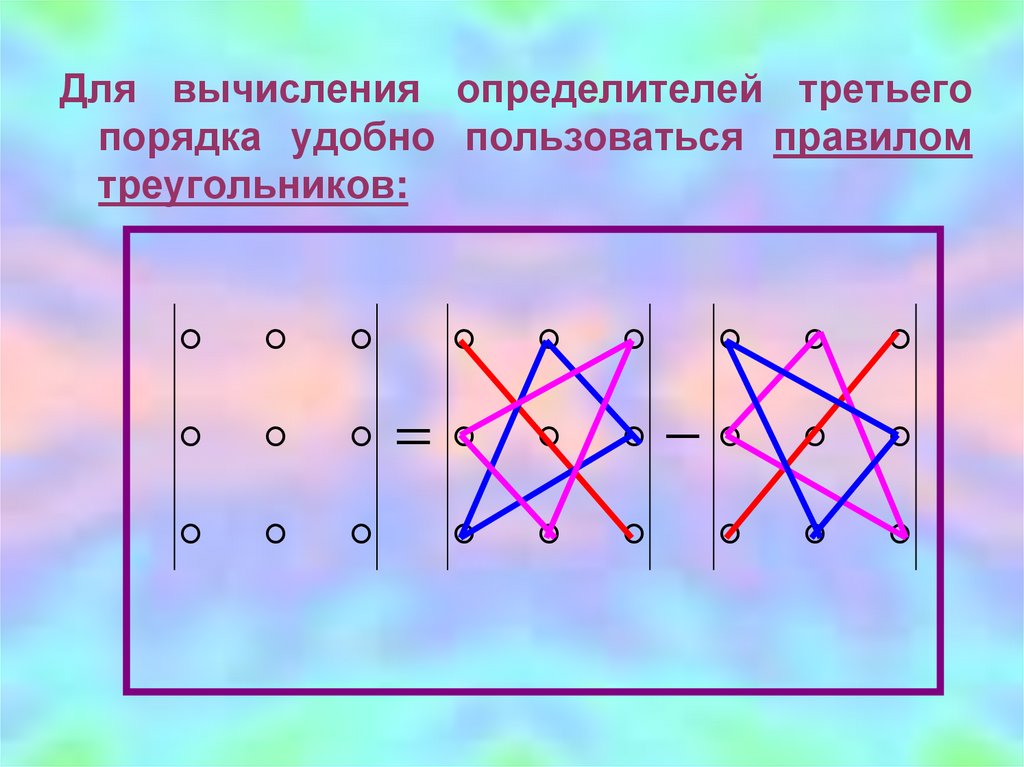
Для вычисления определителей третьегопорядка удобно пользоваться правилом
треугольников:
7.
Вычислить определители матриц:1 2
A
3 5
1 1 1
B 2 1 1
1 1 2
8.
A1
2
3 5
1 5 ( 3) 2 11
1 1 1
B 2 1 1
1 1 2
1 1 2 ( 1) 1 1 1 2 1 1 1 1 ( 1) 2 2 1 1 1 5
9.
Минором некоторого элементаопределителя называется определитель,
полученный из исходного
вычеркиванием строки и столбца,
на пересечении которых стоит
данный элемент.
Минор элемента определителя
обозначается как
M ij
a ij
10.
Алгебраическим дополнениемнекоторого элемента определителя
называется минор этого элемента,
умноженный на (-1)i+j , где i+j – сумма
номеров строки и столбца, на
пересечении которых стоит данный
элемент.
Aij ( 1)
i j
M ij
11.
В частности, минор элементаa11
определителя третьего порядка найдется по
правилу:
a11
a12
a13
a21 a22
a23
a31 a32
a33
a22
M 11
a32
Его алгебраическое дополнение:
1 1
A11 ( 1) M11 M11
a23
a33
12.
Сумма произведений элементов любогостолбца (строки) на алгебраические
дополнения соответствующих
элементов другого столбца (строки)
равна нулю.
13.
Например,пусть дан определитель:
1 1 1
B 2 1 1
1 1 2
Найдем
алгебраические
элементов первой строки:
M 11
1 1
M 12
2 1
1 1
A11 ( 1)
1 2
A12 ( 1)
1 2
1 2
дополнения
2 1 1
(4 1) 3
14.
1 3A13 ( 1)
M 13
2 1
1 2
4 1 3
Умножим каждый элемент первой строки на
алгебраическое
дополнение
соответствующего элемента второй строки
и эти произведения сложим:
2 1 1 ( 3) 1 1 0
15.
1Определитель транспонированной
матрицы равен определителю
исходной матрицы.
A A
T
16.
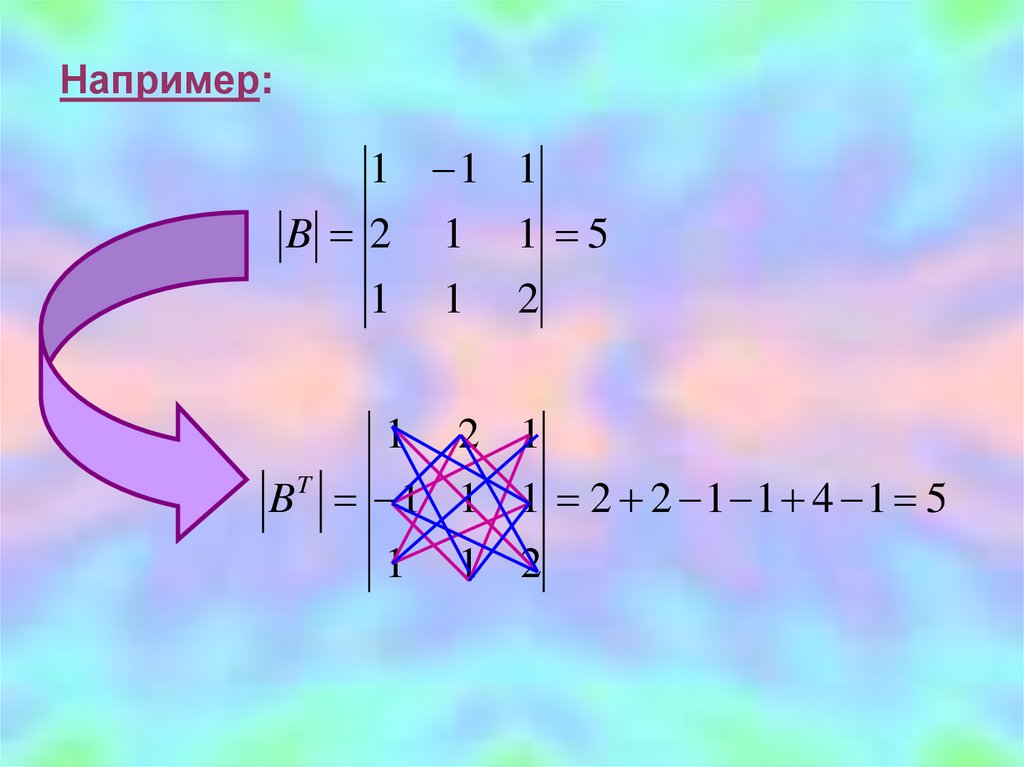
Например:1 1 1
B 2
1
1 5
1
1
2
1
2 1
B 1 1 1 2 2 1 1 4 1 5
T
1
1 2
17.
2Перестановка двух строк или
столбцов определителя
эквивалентна умножению его
на (-1).
18.
Например:1 1 1
B 2
1
1 5
1
1
2
Меняем местами первую и вторую строки:
2
1
1
1 1 1 4 1 1 1 2 2 5
1
1
2
19.
3Если определитель имеет две
одинаковые строки или столбца,
то он равен нулю.
20.
Например:1 1 3
2 2 2 4 4 12 12 4 4 0
2 2 2
21.
4Общий множитель строки или
столбца можно выносить за знак
определителя.
22.
Например:1 1 1
2
2
2 4 2 2 2 4 2 4
1
1
2
Выносим из второй строки множитель 2:
1 1 1
1 1 1
2 2 2 2 1 1 1 2 (2 1 1 1 2 1) 2 2 4
1 1 2
1 1 2
23.
Это свойство можно записать так:Если все элементы некоторой
строки умножить на одно и тоже
число, то определитель
умножается на это число.
24.
5Определитель не изменится, если
к элементам одной строки или столбца
прибавить соответственные элементы
другой строки или столбца,
умноженные на одно и то же число.
25.
Например:1 1 1
B 2
1
1 5
1
1
2
Первую строку умножаем на 2 и складываем
со второй:
1 1 1
4 1 3 2 3 4 1 8 3 5
1
1
2
26.
6Если все элементы некоторой
строки определителя равны нулю, то
определитель тоже равен нулю.
27.
Например:0 0 0
B 2 1 1 0
1 1 2
28.
7Определитель, содержащий две
пропорциональные строки или столбца,
равен нулю.
29.
Например:4 2 2
B 2 1 1 8 2 4 2 8 4 0
1 1 2
30.
8Определитель равен сумме
произведений элементов какойлибо строки или столбца на их
алгебраические дополнения:
n
A ai1 Ai1 ai 2 Ai 2 ... ain Ain aik Aik
k 1
31.
Вычислить определитель:5
1
2
7
3
0
0
2
1
3
4
5
2
0
0
3
32.
Раскладываемстроке:
определитель
по
второй
5 1 2 7
3 0 0 2
1 3 4 5
3 A21 0 A22 0 A23 2 A24 3 A21 2 A24
2 0 0 3
Находим алгебраические дополнения:
=
33.
1 2 7A21 ( 1) 2 1 M 21 3 4 5 (12 0 0 0 18 0) 6
0 0 3
5 1 2
A24 ( 1) 2 4 M 24 1 3 4 0 8 0 12 0 0 4
2 0 0
Подставляем полученный результат:
=
3 6 2 ( 4) 10
34.
Таким образом, вычисление определителя nпорядка
сводится
к
вычислению
n
определителей n-1 порядка.
Во многих случаях такое вычисление может
оказаться очень громоздким.
Задача существенно упростится, если в
определителе имеются нули. Например, если
какая-то строка или столбец содержат только
один ненулевой элемент, то раскладывая
определитель по этой строке (столбцу), мы
получим только одно ненулевое слагаемое.
Поэтому удобно преобразовывать заданный
определитель, чтобы получить в нем нули.
35.
Рассмотрим предыдущий пример:5
1
2
7
3
0
0
2
1
3
4
5
2
0
0
3
В данном определителе уже имеются нули,
например, в третьем столбце их два.
Сделаем так, чтобы в нем остался один
ненулевой элемент.
Для этого умножим второй столбец на -2 и
сложим его с третьим:
36.
25
1
2
7
5
1
0
7
3
0
0
2
3
0
0
2
1
3
4
5
1
3
2
5
2
0
0
3
2
0
0
3
5
1
7
2 3
0
2 2 0 4 0 0 9 0 10
2
0
3






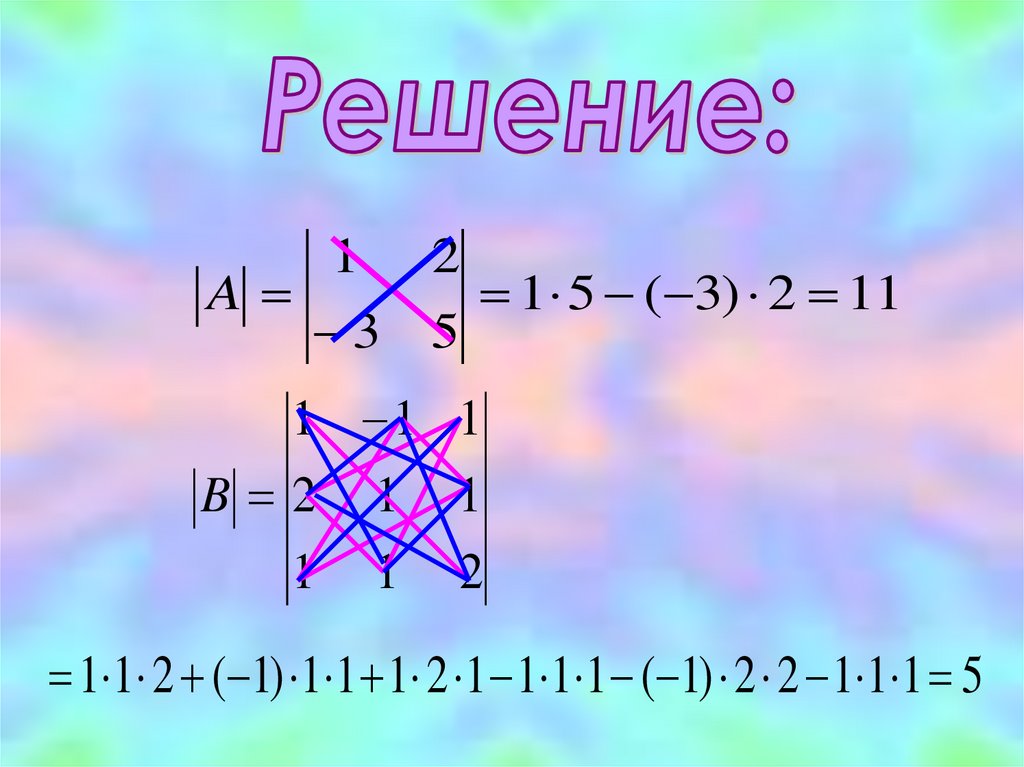


























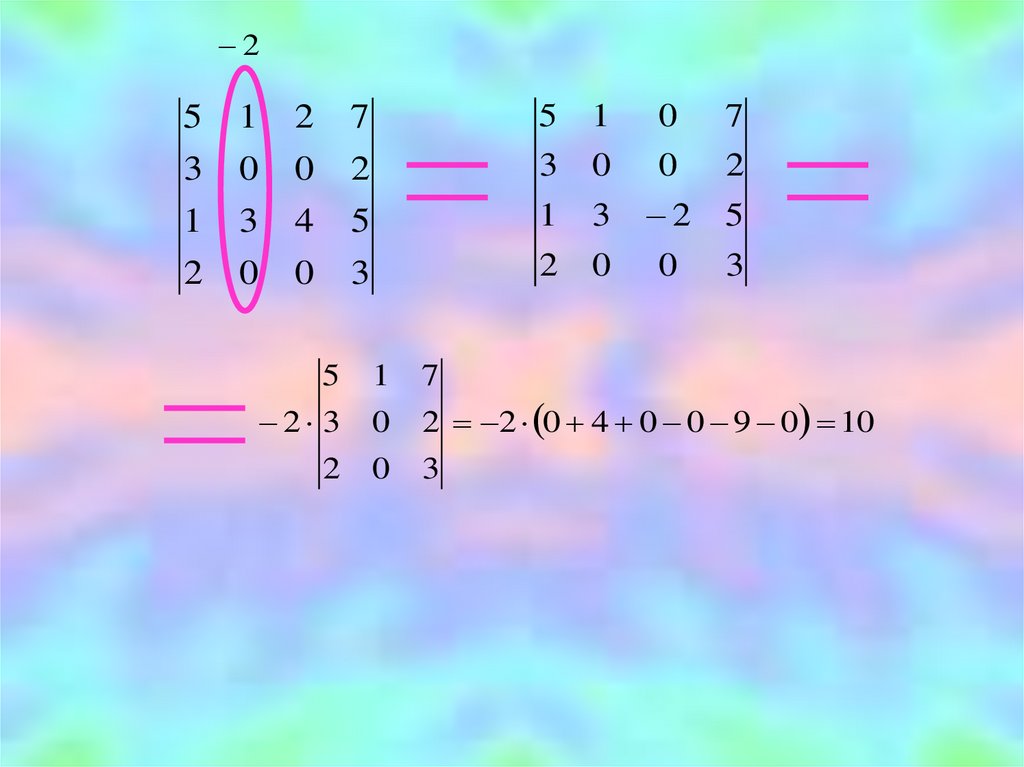
 mathematics
mathematics








