Лекция_5_формулы_01.11.2023

1. Лекция №5 Вычислительная математика

Санкт-Петербургский политехнический университет Петра Великого
Лекция №5
Вычислительная математика
Воскобойников С.П.
Доцент ВШ ПИ ИКНТ, к.ф.-м.н.
voskob_sp@spbstu.ru
01.11.2023

2. Содержание

• Спектральное разложение. Разложение
Шура.
• Свойства матриц ATA и AAT.
Сингулярное разложение. Полярное
разложение.
• Алгебраическая проблема собственных
значений.
• Прямой и обратный степенной метод.
Сдвиги.
• QR-алгоритм.
• Вычисление сингулярного разложения

3. Спектральное разложение

Ax x,
Axi i xi ,
1
2
.
.
.
,
n
i 1,2,..., n
X x1
x2 . . . xn ,
A матрица простой структуры
AX X ,
A X X 1,
A AT ,
X T X E,
A X X T ,
A вещественные, если A AT

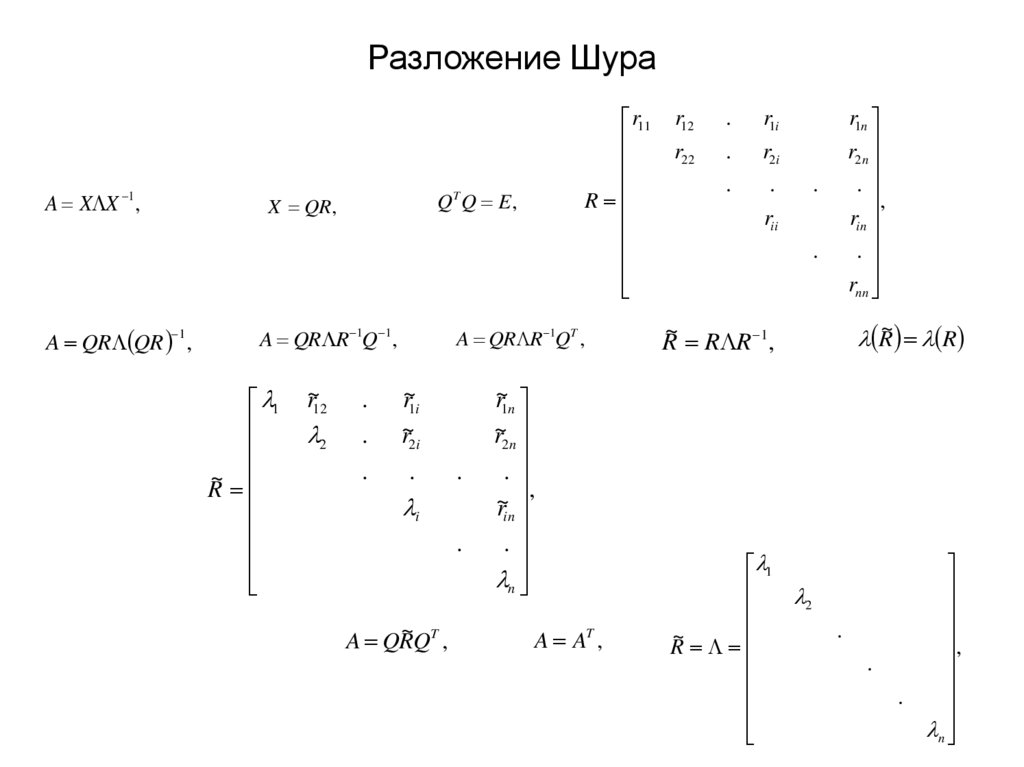
4. Разложение Шура

1
A X X ,
QT Q E ,
X QR ,
A QR QR ,
1
A QR R 1QT ,
A QR R 1Q 1 ,
1
~
R
~
r12
2
r11
R
.
.
.
~
r1i
~
r
2i
.
.
i
.
~QT ,
A QR
~
r1n
~
r2 n
.
,
~
rin
.
n
A AT ,
r12
r22
.
.
.
r1i
r2i
.
rii
r1n
r2 n
.
,
rin
.
rnn
.
.
R~ R
~ R R 1 ,
R
1
2
~
R
.
.
.
,
n

5. Разложение Шура

A AT ,
1 A j ,
2 A j ,
~Q* ,
A QR
~QT ,
A QR
j 1,
qij* q ji
~ комплексные
Qи R
~ вещественные
Qи R
~
R
~
r13
~
r
23
3
.
.
.
.
.
.
.
.
~
r1n
~
r2 n
.
,
~
rin
.
n

6. Свойства матриц ATA и AAT

Bx , x xT Bx ,
i B 0,
B BT
B AT A
det A 0
xT AT Ax Ax Ax yT y 0,
xT Bx xT AT Ax,
T
y 0,
y Ax
x 0
B V V T
n
x Bx x V V x y y i yi2 0,
T
T
T
y 0, i 0
T
i 1
C AAT
Cx, x 0,
C CT
x 0
AT A AAT ,
AT Ax x,
x A x,
AAT AT
1
T 1
x,
Ax AT
1
x,
y AT
1
AAT y y,
i C 0,

7. Сингулярное разложение

где V матрица из разложения B AT A V V T
U~ AVD,
T
U~TU~ AVD AVD DTV T AT AVD
DTV T AT AVD DTV TV V TVD D D
D
1
2
U~TU~ E ,
A U~ V T ,
D D E ,
1
U~ AVD AV 2 ,
1
U~ 2V T A,
T
T
AAT U~ V T U~ V T U~ V T V T TU~T U~ 2U~T ,
2 ,
U~ U
A U V T ,
1
2
U TU E
.
.
i i
,
.
n
V TV E
i 0
1
2

8. Полярное разложение

A U V T ,
W1 U U T ,
A U U TUV T ,
Z UV T
T
Z T Z UV T UV T VU TUV T E
W1T W1
A W1Z
A UV TV V T Z W2 ,
W2 V V T ,
W2T W2

9. Алгебраическая проблема собственных значений

Pn n an 1 n 1 ... a1 a0 0,
det A E 0,
1, 2 ,..., n
A i E xi 0, i 1,2,..., n
Axi i xi ,
20 20
19 20
18 20
A
.
20 20
19 20
18 20
~
A
.
.
2
.
2
A E x 0,
Ax x,
A n n
20
1
20
1
yi cxi , c 0
20
P20 k 0,
k k , k 1,2,...,20
k 1
~ ( ) P ( ) 2019
P
20
20
10 10
~k C ,

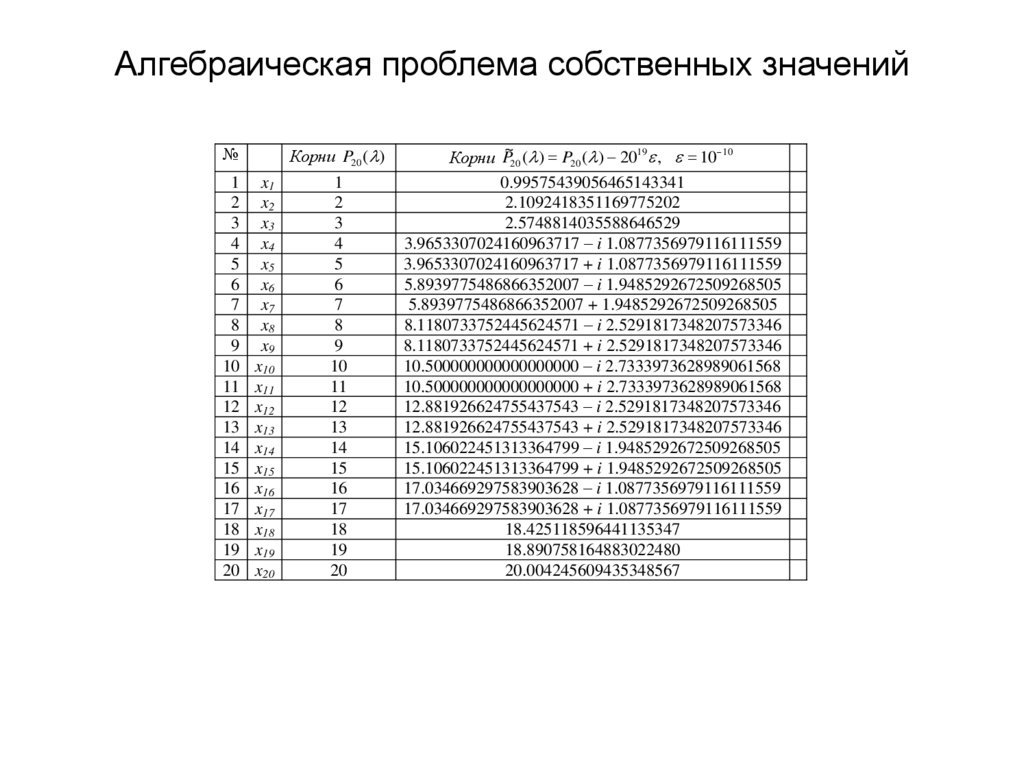
10. Алгебраическая проблема собственных значений

Корни P20 ( )
№
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
x1
x2
x3
x4
x5
x6
x7
x8
x9
x10
x11
x12
x13
x14
x15
x16
x17
x18
x19
x20
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
~ ( ) P ( ) 2019 , 10 10
Корни P
20
20
0.99575439056465143341
2.1092418351169775202
2.5748814035588646529
3.9653307024160963717 – i 1.0877356979116111559
3.9653307024160963717 + i 1.0877356979116111559
5.8939775486866352007 – i 1.9485292672509268505
5.8939775486866352007 + 1.9485292672509268505
8.1180733752445624571 – i 2.5291817348207573346
8.1180733752445624571 + i 2.5291817348207573346
10.500000000000000000 – i 2.7333973628989061568
10.500000000000000000 + i 2.7333973628989061568
12.881926624755437543 – i 2.5291817348207573346
12.881926624755437543 + i 2.5291817348207573346
15.106022451313364799 – i 1.9485292672509268505
15.106022451313364799 + i 1.9485292672509268505
17.034669297583903628 – i 1.0877356979116111559
17.034669297583903628 + i 1.0877356979116111559
18.425118596441135347
18.890758164883022480
20.004245609435348567

11. Частичная проблема собственных значений. Идея степенного метода для определения λmax

max ?
x ?
A матрица простой структуры, т.е. имеет n л.н.з. векторов si
1 2 ... n
x 0 произвольный ненулевой вектор,
k 1,2,...
x k Ax k 1
x
0
n
i si ,
i 1
x
k
A x
k
0
n
n
n
A i si i A si i ik si 1 1k s1 2 k2 s2 ... n kn sn n kn sn ,
k
k
i 1
sn
i 1
1
k
x
,
k
n n
i 1
xi k
n k 1
xi

12. Частичная проблема собственных значений. Идея степенного метода для определения λmax

x 0 произвольный ненулевой вектор,
k 1,2,...
y Ax k 1 ,
x k
y
,
y
sn k x k ,
k
n
xi k
k 1
xi
nk nk 1 nk R A ,
R A ,

13. Частичная проблема собственных значений. Идея обратного степенного метода для определения λmin

A 1 xi i 1 xi ,
x 0 произвольный ненулевой вектор,
k 1,2,...
x k A 1 x k 1
x
0
n
i si ,
i 1
x
k
k
A x
0
A
k
n
n
n
s A s s s s ... s s ,
i 1
i i
k
i 1
i
s1
xi k
k 1
xi
1
1
i
1
i 1
k
i i
i
k
1 1 1
k
x
,
k
1 1
xi k 1
1 k
xi
k
2 2 2
k
n n n
k
1 1 1

14. Частичная проблема собственных значений. Идея обратного степенного метода для определения λmin

x 0 произвольный ненулевой вектор,
PA LU
k 1,2,...
Lz Px k 1 ,
Uy z ,
x k
y
,
y
s1 k x k ,
k
1
xi k 1
k
xi
1 k 1 k 1 1 k R A ,

15. Частичная проблема собственных значений. Идея обратного степенного метода со сдвигами

Ax x,
A E ,
A E x x,
A E 1 x 1 x,
x 0 произвольный ненулевой вектор,
k 1,2,...
x k A E x k 1
1
x
0
n
i si ,
i 1
x
k
A E x
k
0
A E
k
n
n
s A E s ,
i i
i 1
x
k
n
i 1
k
i
i
i i si 1 1 s1 2 2 s2 ... i i si n n sn ,
k
k
k
i 1
i
x k i i si
k
si cx k ,
k
k

16. Частичная проблема собственных значений. Идея обратного степенного метода со сдвигами

i
~H T , A
~ верхняя форма Хессенберга
A HA
~
x 0 произвольный ненулевой вектор,
k 1,2,...
d HT~
x k 1
A~ E y d ,
y
~
x k ,
y
si k H~
x k ,

17. Полная проблема собственных значений. QR-алгоритм

~QT
A QR
QT Q E
A0 A
A0 Q0 R0
1
~
R
A1 R0Q0
~
r12
.
2
.
.
~
r1i
~
r
2i
.
.
i
.
A1 Q0T A0Q0
A1 A0 A
A0 A
k 1,2,...
Ak 1 Qk 1Rk 1
Ak Rk 1Qk 1
Ak QkT 1 Ak 1Qk 1
Ak QkT 1...Q0T A0Q0 ...Qk 1
~
lim Ak R
k
~
r1n
~
r2 n
.
,
~
rin
.
n

18. Полная проблема собственных значений. QR-алгоритм

~
1. A H T AH
~ A
~
A
0
2. k 1,2,...
~
Ak 1 Qk 1Rk 1
1
~ R
~
lim A
k
k
~
r12
2
~ R Q
A
k
k 1 k 1
.
.
.
~
r1i
~
r
2i
.
.
i
.
~
r1n
~
r2 n
.
~
rin
.
n
3. вычисление собственных векторов
~ матрицы верхней формы Хессенберга
A
обратным степенным методом со сдвигами
4. восстановление собственных векторов
A исходной матрицы

19. Полная проблема собственных значений. QR-алгоритм

Замечание 1. Верхняя форма Хессенберга сохраняется на этапе 2
~
~
Это видно из равенства Ak Rk 1 Ak 1Rk 11
Замечание 2. Если A AT , то верхняя форма Хессенберга
~ диагональной.
является трёхдиагональной матрицей, R
Замечание 3. QR разложение на этапе 2 выгодно осуществлять
с помощью преобразований Гивенса. Информация о преобразованиях
должна сохраняться, если требуется вычислять собственные векторы.
Замечание 4. Информация о преобразованиях , сделанных на этапе 1 для
приведения матрицы к верхней форме Хессенберга должна
сохраняться, если требуется вычислять собственные векторы.

20. Полная проблема собственных значений. QR-алгоритм

Замечание 5. Если A AT , то целесообразно выполнить перед этапом 1
" уравновешивание" матрицы A. Для этого подбирается диагональн ая
матриа D следующего вида
d11
d 22
D
.
.
.
d nn
где dii k i , основание системы счисления ЭВМ , ki натуральные числа, включая 0.
Исходная матрица преобразуется преобразованием подобия DAD 1 ,
так чтобы у преобразованной матрицы, норма была меньше, чем у исходной, и
нормы одноимённых строк и столбцов были примерно одинаковы. После этого новая матрица
преобразуется к форме Хессенберга ( этап 1), а после выполнения этапа 4, производится
обратное преобразование для воостановления собственных векторов исходной матрицы.
EISPACK
LINPACK
LAPACK

21. Вычисление сингулярного разложения

A U V T ,
U TU E ,
диагональная
V TV E ,
1. A U~DV~T ,
d11
D
d12
d 22
d 23
.
.
.
.
.
.
d n 1,n 1
2. k 1,2,...
Dk 1 Qk 1Rk 1
1
2
lim Dk
k
.
,
d n 1,n
d n ,n
Dk Rk 1Qk 1
.
.
i
.
.
.
n
3. Применение ортогональных преобразований , накопленных
на этапе 1 и 2 для вычисления U и V .