Similar presentations:
Geometricheskiy_smysl_proizvodnoy_2
1. Геометрический смысл производной
Повторение2.
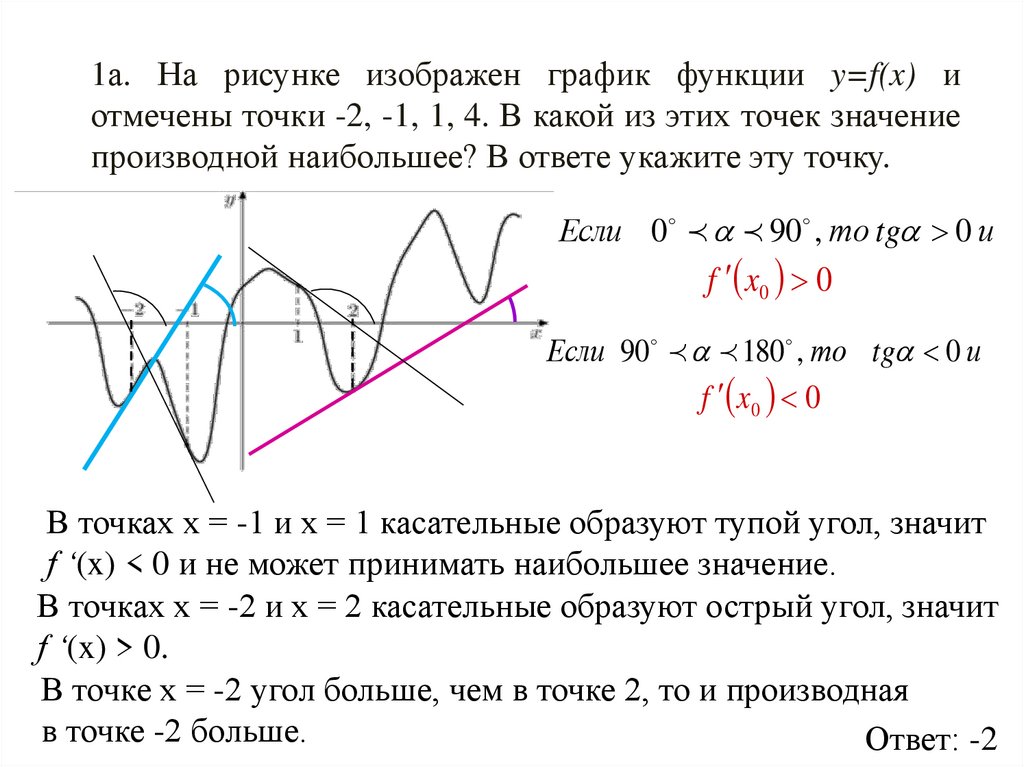
1а. На рисунке изображен график функции y=f(x) иотмечены точки -2, -1, 1, 4. В какой из этих точек значение
производной наибольшее? В ответе укажите эту точку.
Если 0 90 , то tg 0 и
f x 0 0
Если 90 180 , то tg 0 и
f x 0 0
В точках х = -1 и х = 1 касательные образуют тупой угол, значит
f ‘(x) < 0 и не может принимать наибольшее значение.
В точках х = -2 и х = 2 касательные образуют острый угол, значит
f ‘(x) > 0.
В точке х = -2 угол больше, чем в точке 2, то и производная
в точке -2 больше.
Ответ: -2
3.
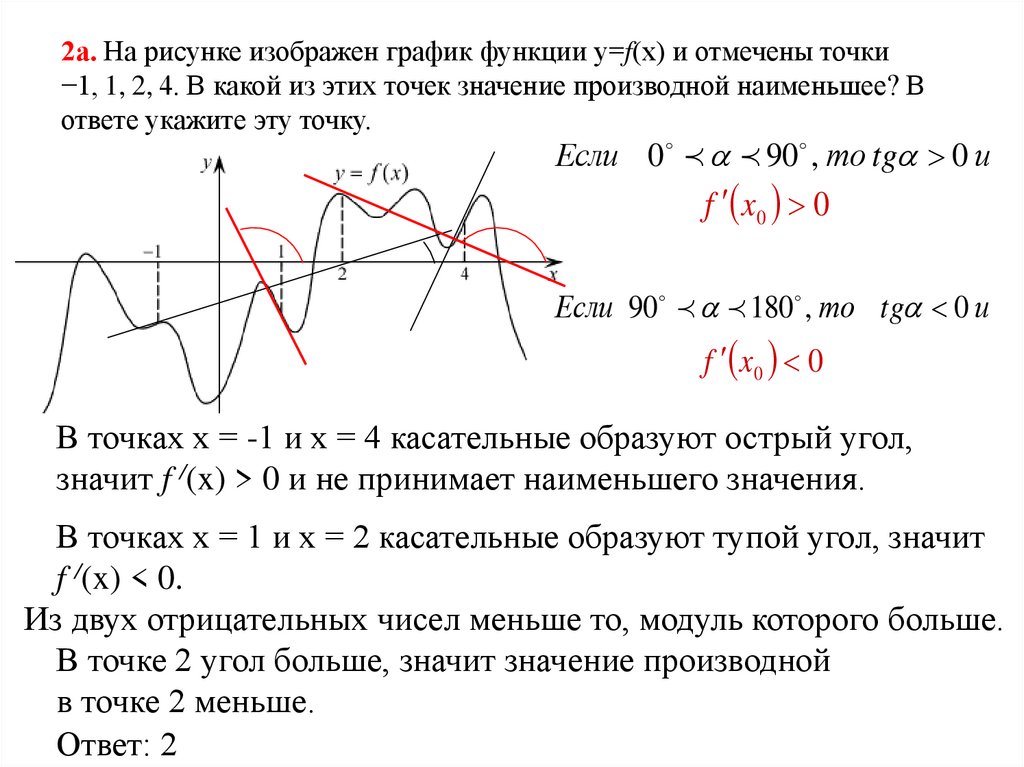
2а. На рисунке изображен график функции y=f(x) и отмечены точки−1, 1, 2, 4. В какой из этих точек значение производной наименьшее? В
ответе укажите эту точку.
Если 0 90 , то tg 0 и
f x 0 0
Если 90 180 , то tg 0 и
f x 0 0
В точках х = -1 и х = 4 касательные образуют острый угол,
значит f /(x) > 0 и не принимает наименьшего значения.
В точках х = 1 и х = 2 касательные образуют тупой угол, значит
f /(x) < 0.
Из двух отрицательных чисел меньше то, модуль которого больше.
В точке 2 угол больше, значит значение производной
в точке 2 меньше.
Ответ: 2
4.
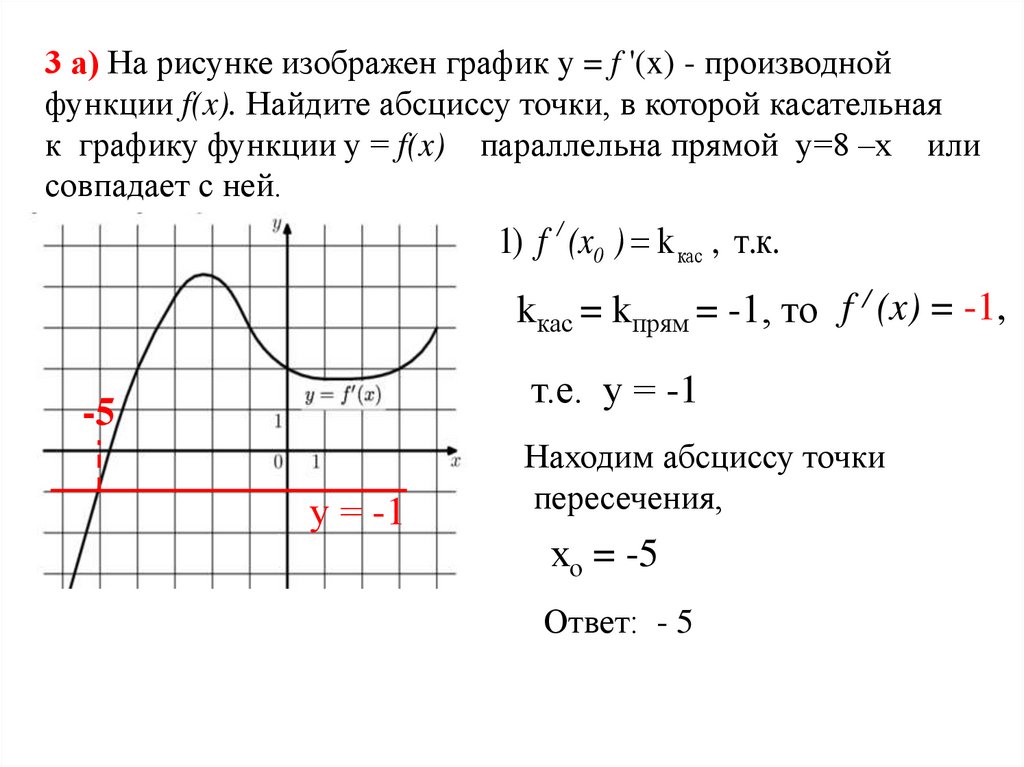
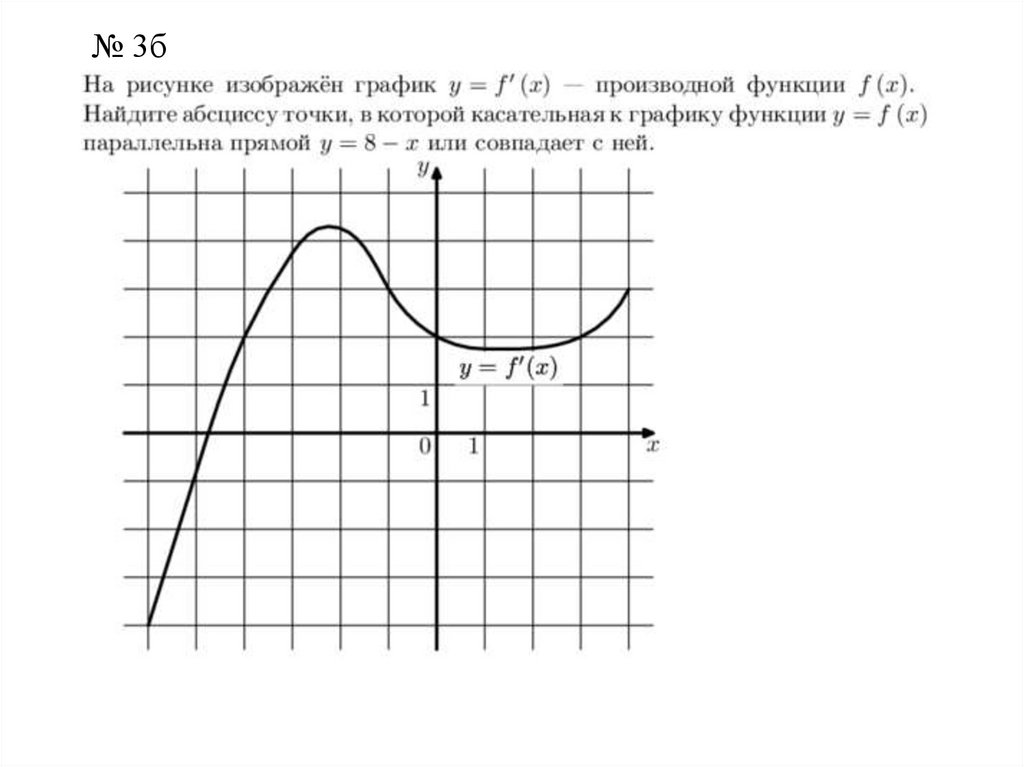
3 а) На рисунке изображен график y = f '(x) - производнойфункции f(x). Найдите абсциссу точки, в которой касательная
к графику функции у = f(x) параллельна прямой у=8 –х или
совпадает с ней.
1) f / (x0 ) k кас , т.к.
kкас = kпрям = -1, то f / (x) = -1,
т.е. у = -1
-5
у = -1
Находим абсциссу точки
пересечения,
хо = -5
Ответ: - 5
5.
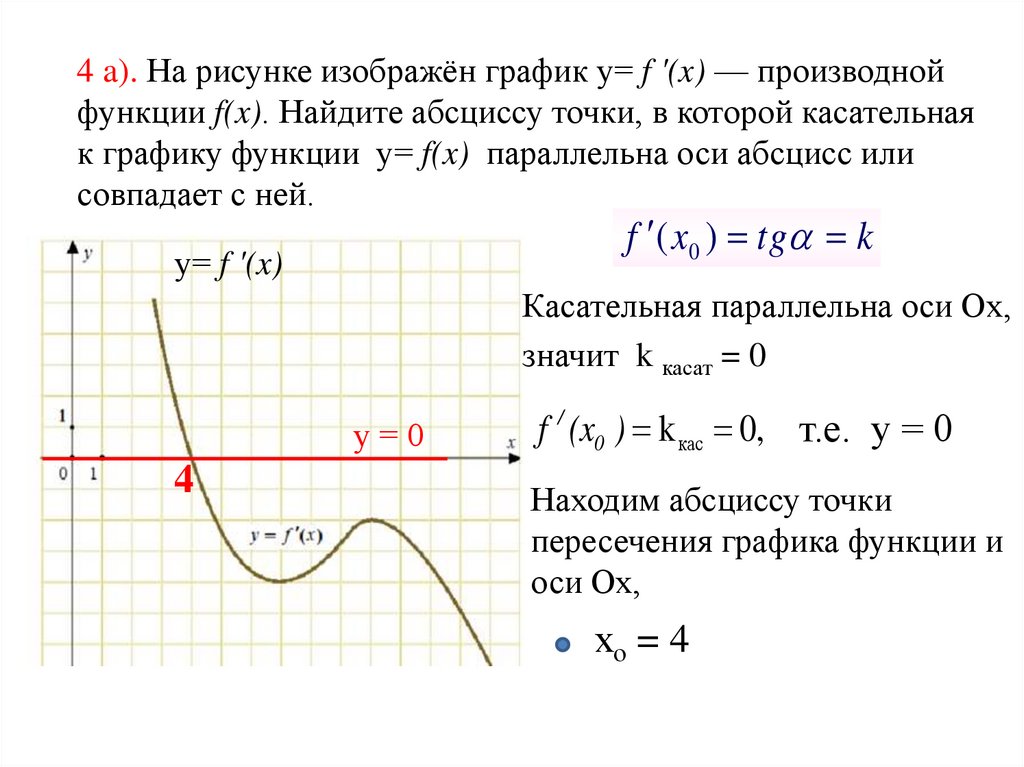
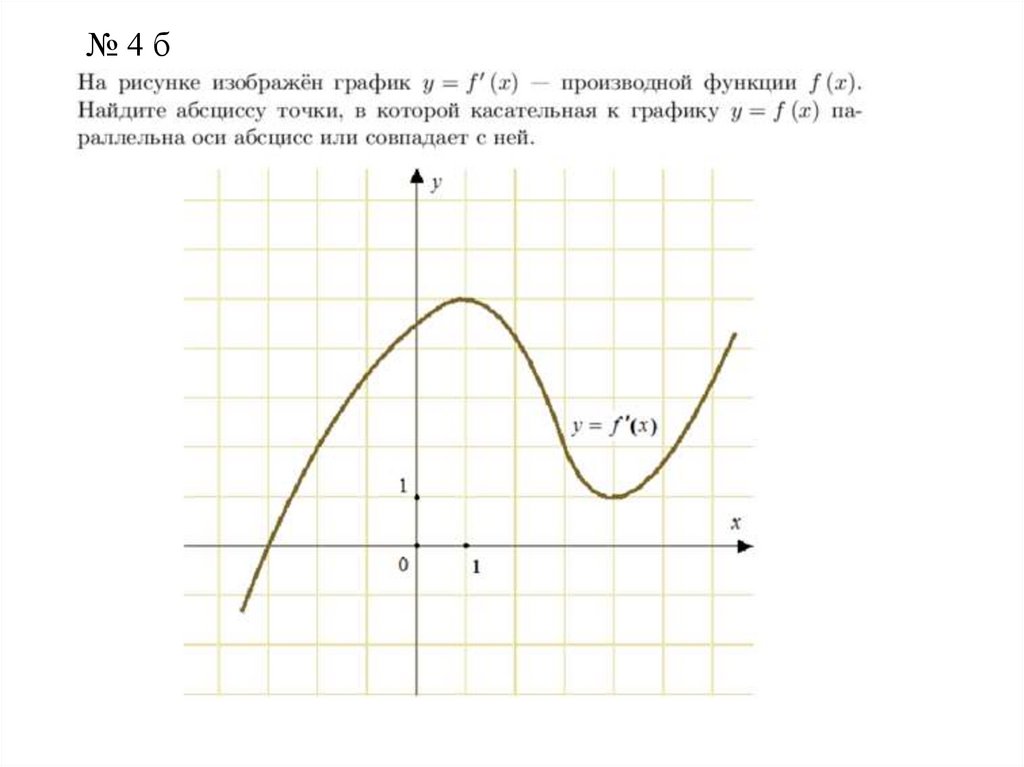
4 a). На рисунке изображён график у= f '(x) — производнойфункции f(x). Найдите абсциссу точки, в которой касательная
к графику функции у= f(x) параллельна оси абсцисс или
совпадает с ней.
f ( x0 ) tg k
у= f '(x)
Касательная параллельна оси Ох,
значит k касат = 0
у=0
4
f / (x0 ) k кас 0, т.е. у = 0
Находим абсциссу точки
пересечения графика функции и
оси Ох,
хо = 4
6.
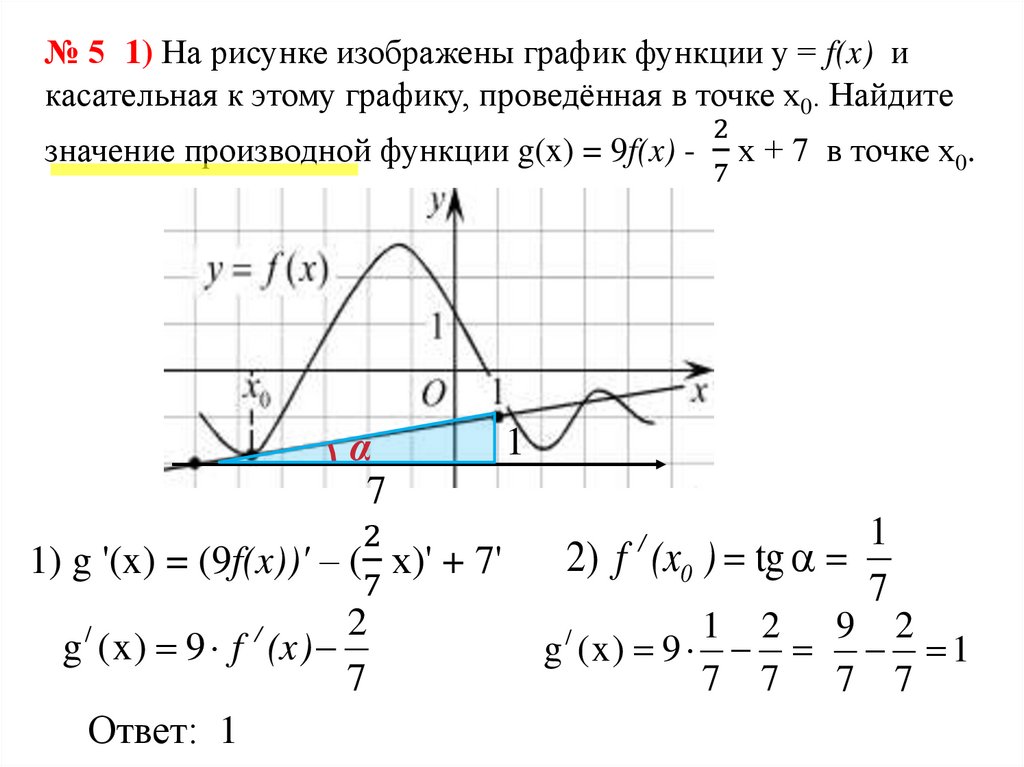
№ 5 1) На рисунке изображены график функции у = f(x) икасательная к этому графику, проведённая в точке x0. Найдите
2
значение производной функции g(x) = 9f(x) - х + 7 в точке x0.
7
α
7
2
1) g '(x) = (9f(x))' – ( х)' + 7'
7
2
g ( x ) 9 f (x)
7
Ответ: 1
/
/
1
1
2) f (x0 ) tg
7
/
1 2 9 2
g (x) 9 1
7 7 7 7
/
7.
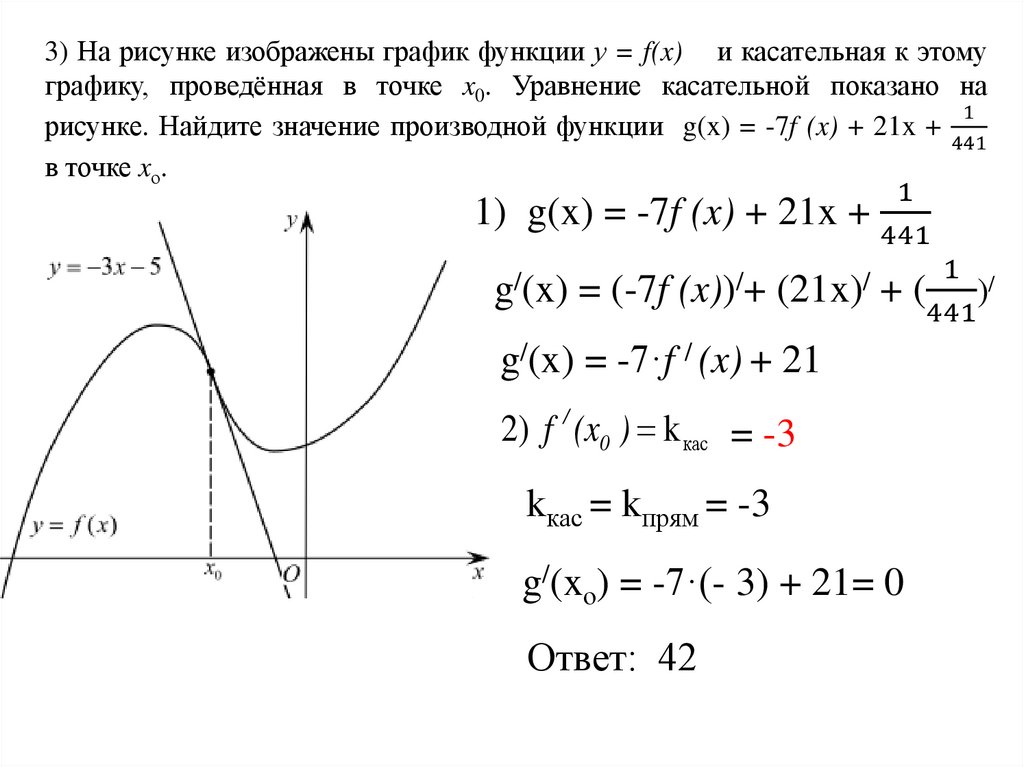
3) На рисунке изображены график функции у = f(x) и касательная к этомуграфику, проведённая в точке x0. Уравнение касательной показано на
1
рисунке. Найдите значение производной функции g(x) = -7f (x) + 21x +
441
в точке xо.
1
1) g(x) = -7f (x) + 21x +
441
1 /
/
/
/
g (x) = (-7f (x)) + (21x) + ( )
441
g/(x) = -7·f / (x) + 21
2) f / (x0 ) k кас = -3
kкас = kпрям = -3
g/(xо) = -7·(- 3) + 21= 0
Ответ: 42
8.
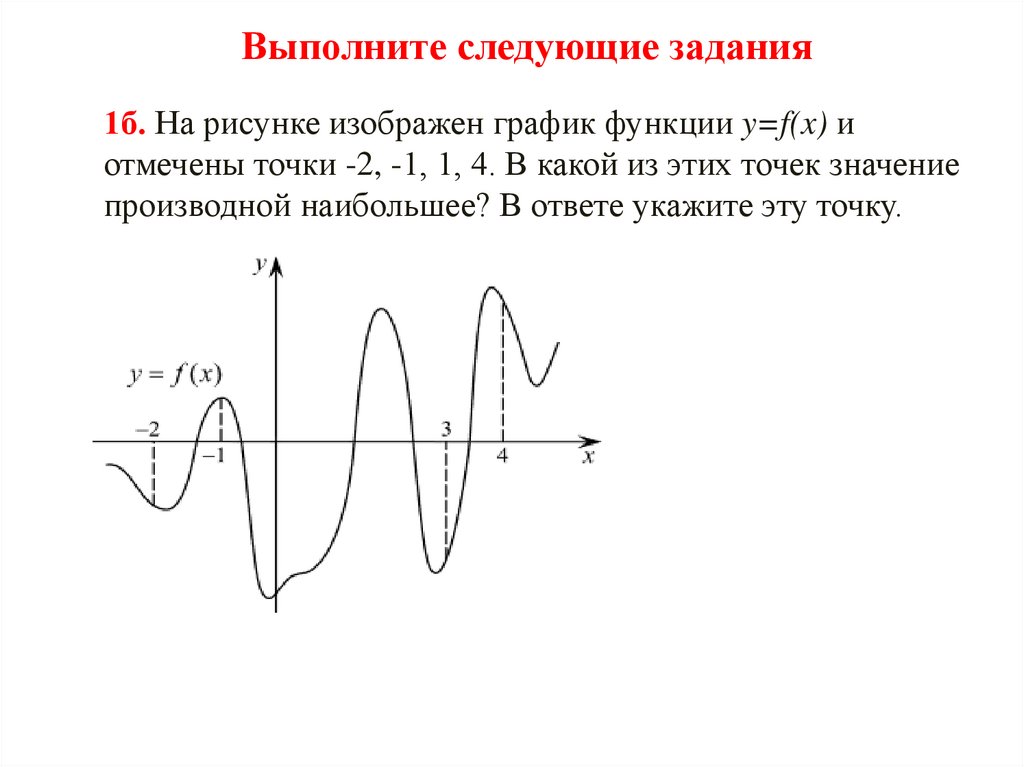
Выполните следующие задания1б. На рисунке изображен график функции y=f(x) и
отмечены точки -2, -1, 1, 4. В какой из этих точек значение
производной наибольшее? В ответе укажите эту точку.
9.
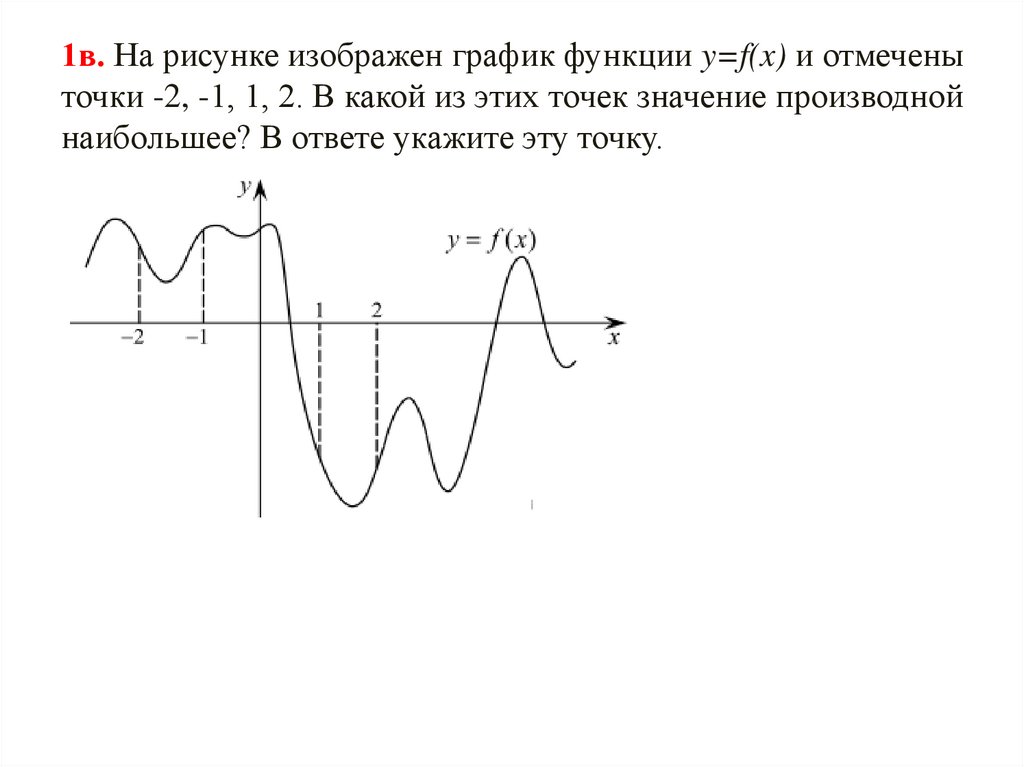
1в. На рисунке изображен график функции y=f(x) и отмеченыточки -2, -1, 1, 2. В какой из этих точек значение производной
наибольшее? В ответе укажите эту точку.
10.
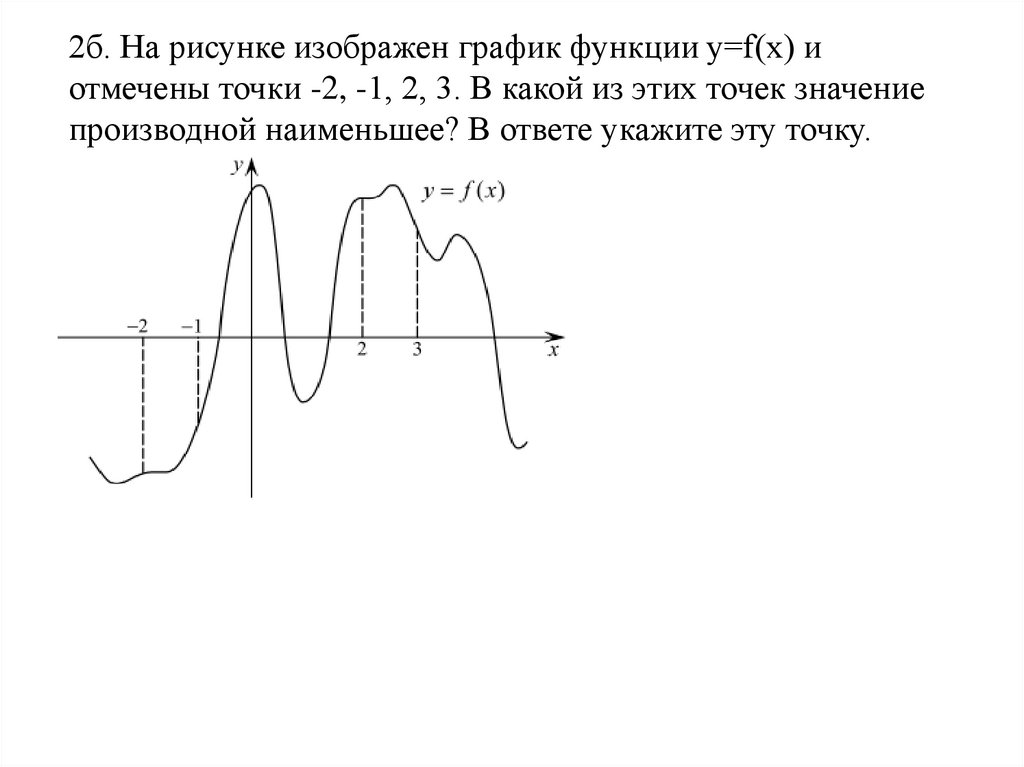
2б. На рисунке изображен график функции y=f(x) иотмечены точки -2, -1, 2, 3. В какой из этих точек значение
производной наименьшее? В ответе укажите эту точку.
11.
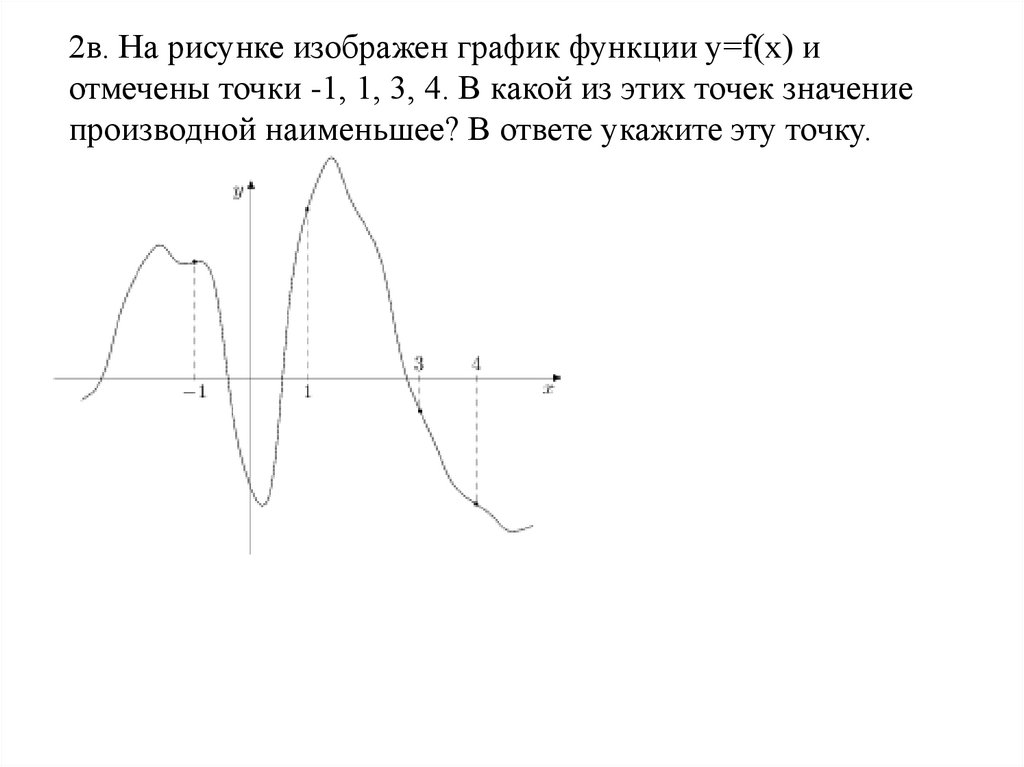
2в. На рисунке изображен график функции y=f(x) иотмечены точки -1, 1, 3, 4. В какой из этих точек значение
производной наименьшее? В ответе укажите эту точку.

 mathematics
mathematics








