Геометрический смысл производной в заданиях КИМ ЕГЭ

1. Урок 93

Геометрический смысл
производной
в заданиях КИМ ЕГЭ
УРОК 93

2.

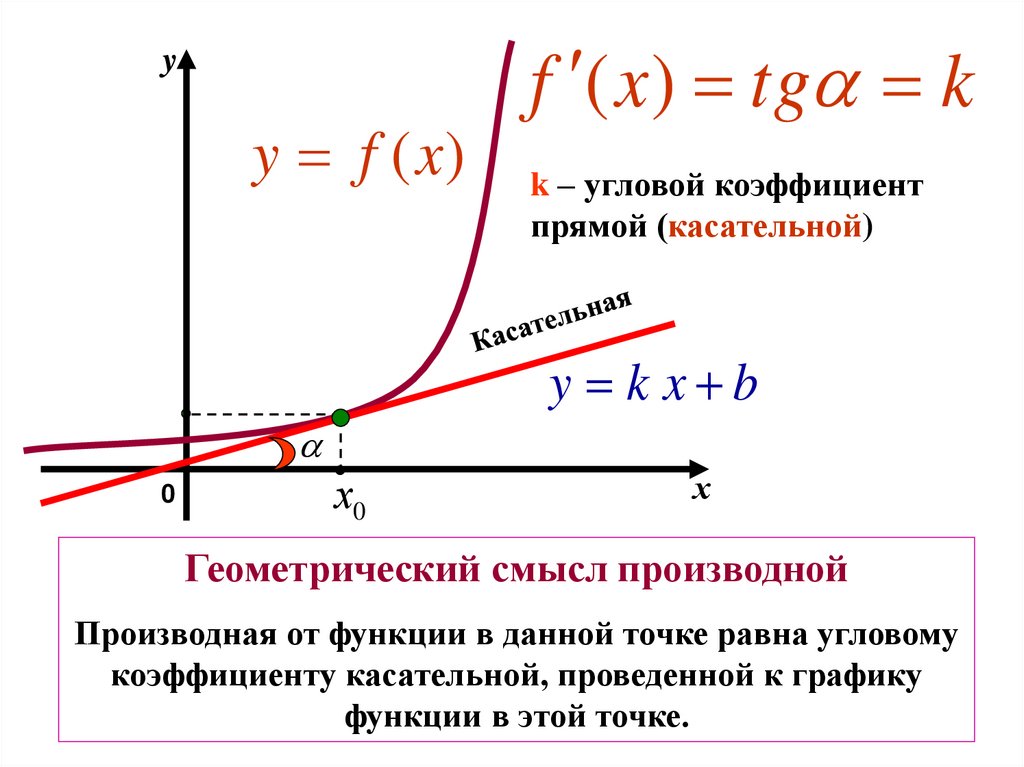
y
y f (x)
f ( x ) tg k
k – угловой коэффициент
прямой (касательной)
y k x b
0
х0
х
Геометрический смысл производной
Производная от функции в данной точке равна угловому
коэффициенту касательной, проведенной к графику
функции в этой точке.

3.

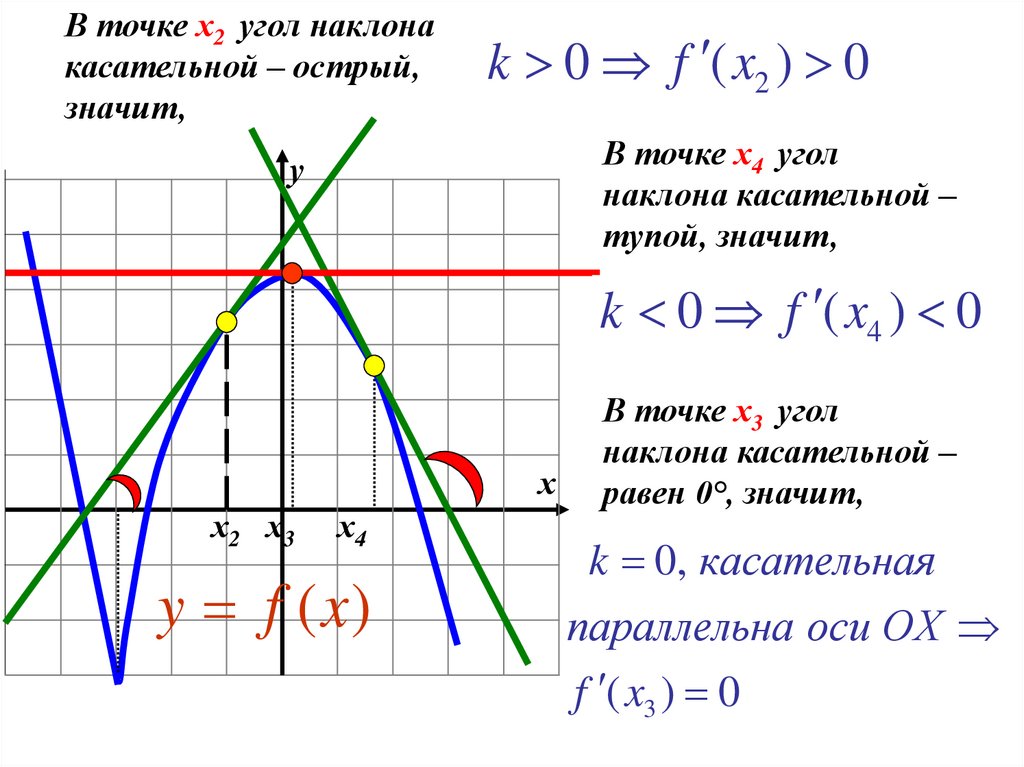
В точке х2 угол наклона
касательной – острый,
значит,
k 0 f ( x2 ) 0
В точке х4 угол
наклона касательной –
тупой, значит,
у
k 0 f ( x4 ) 0
х
х2 х3
х4
y f (x)
В точке х3 угол
наклона касательной –
равен 0°, значит,
k 0, касательная
параллельна оси ОХ
f ( x3 ) 0

4.

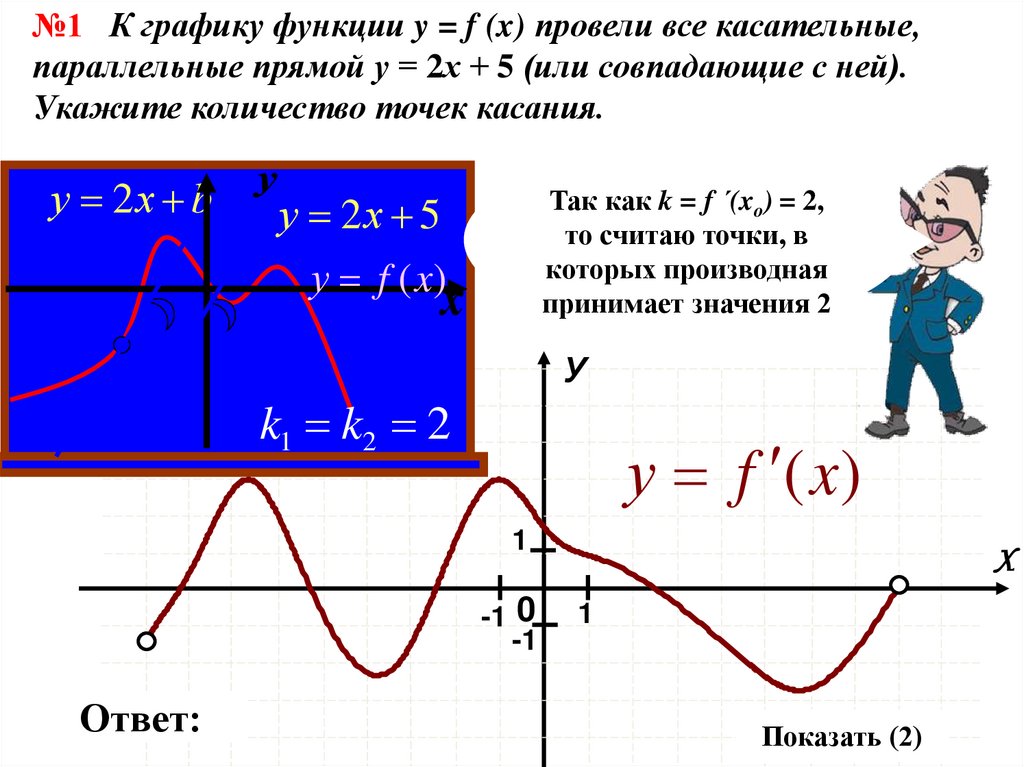
№1 К графику функции y = f (x) провели все касательные,
параллельные прямой у = 2х + 5 (или совпадающие с ней).
Укажите количество точек касания.
у 2х b
Так как k = f ´(xo) = 2,
то считаю точки, в
которых производная
принимает значения 2
у 2х 5
у f (x)
У
k1 k2 2
у f (x )
1
-1 0
-1
Ответ:
Х
1
Показать (2)

5.

У
у f (x )
1
-1 0
-1
k f ( xo ) 2
В5
-4
3
10 х
х
Х
1

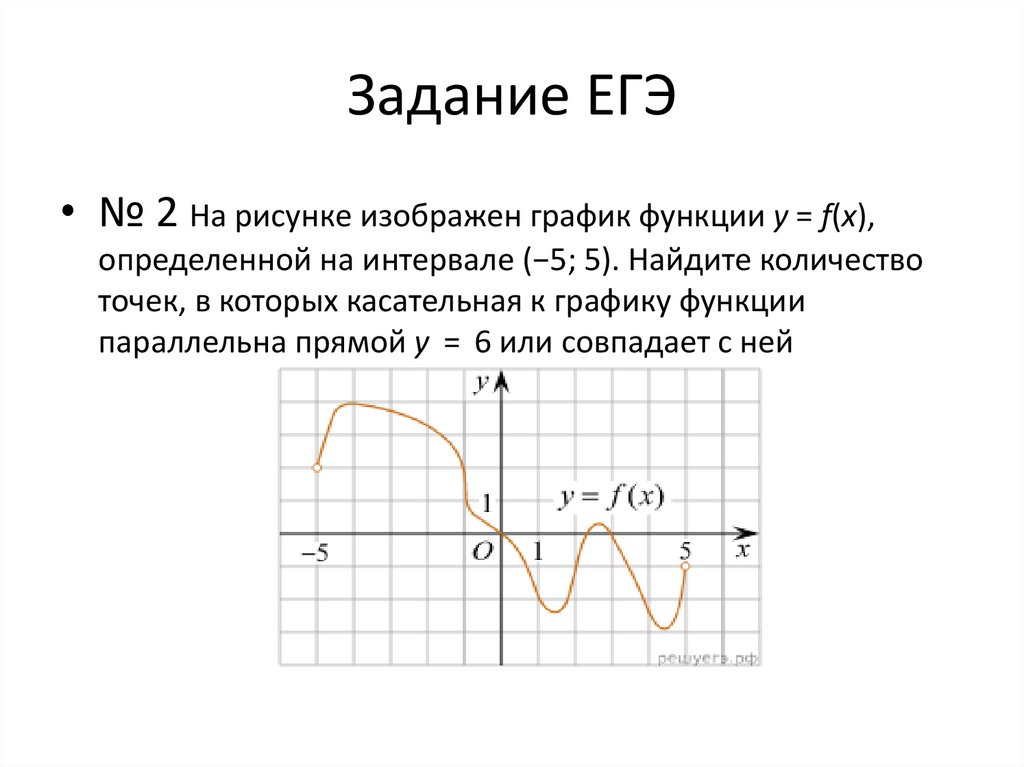
6. Задание ЕГЭ

• № 2 На рисунке изображен график функции y = f(x),
определенной на интервале (−5; 5). Найдите количество
точек, в которых касательная к графику функции
параллельна прямой y = 6 или совпадает с ней

7. Задание ЕГЭ

• № 3На рисунке изображен график производной
функции f(x), определенной на интервале (−10; 2).
Найдите количество точек, в которых касательная к
графику функции f(x) параллельна прямой y = −2x − 11 или
совпадает с ней.

8.

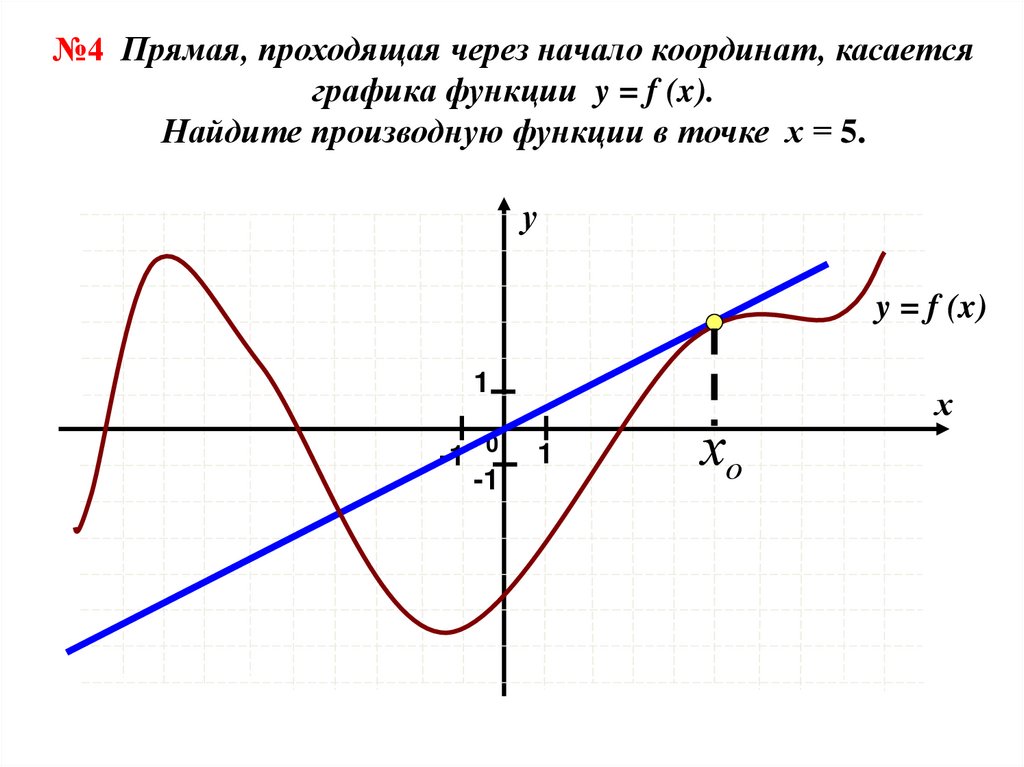
№4 Прямая, проходящая через начало координат, касается
графика функции y = f (x).
Найдите производную функции в точке х = 5.
у
y = f (x)
1
-1
0
-1
1
хо
х

9.

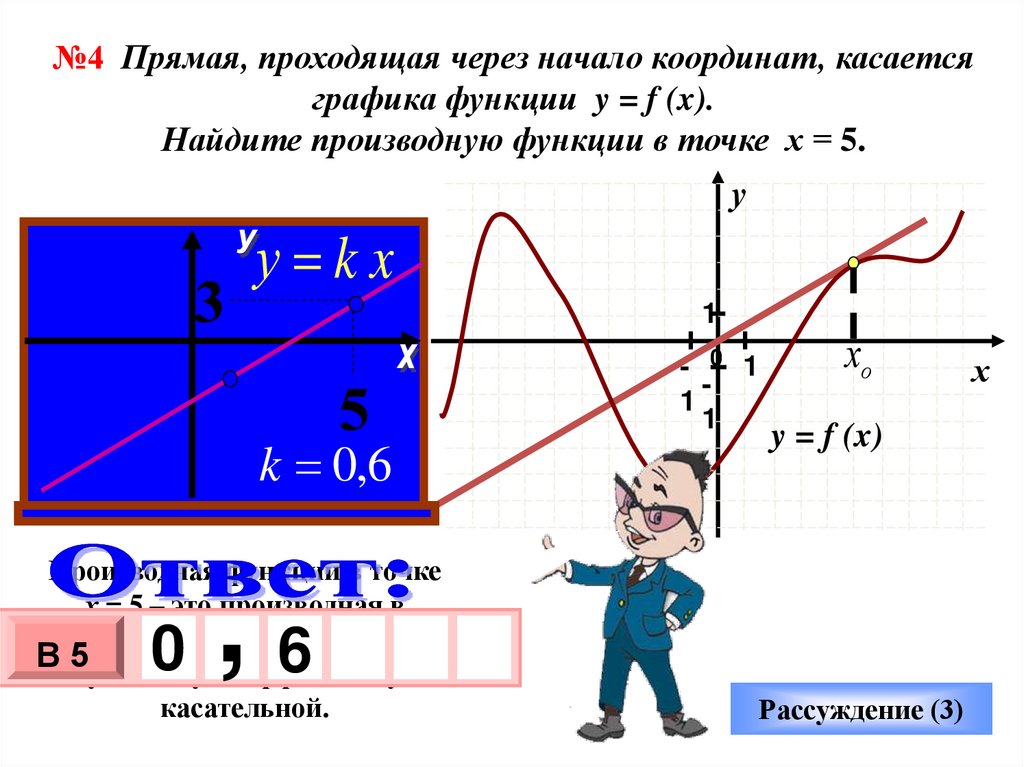
№4 Прямая, проходящая через начало координат, касается
графика функции y = f (x).
Найдите производную функции в точке х = 5.
у
у kx
1
k 0,6
Производная функции в точке
х = 5 – это производная в
х
3
точке касания хо, а она
равна
1 0 х
В 5угловому коэффициенту
касательной.
,
- 6
- 0 1
1
1
хо
y = f (x)
0
Рассуждение (3)
х

10.

№5 К графику функции y = f (x) (на рисунке его нет) провели
касательные под углом 135° к положительному направлению
оси Ох. На рисунке изображён график производной функции.
Укажите количество точек касания
уугол
наклона
f (x )
У
касательной
к
оси
Ох
:
1
tg k f -1 (-1xo1 )
0
tg 135 1 f ( xo )
o
В5
-4
Ответ (2)
3
10 х
х
Рассуждение (2)
Х

11.

№6 Найдите значение производной функции в точке касания
2 1
f ( a ) tg 0,5.
4 2
В5
f (а ) y tg
y=g(x)
угол наклона
1 йa к
касательно
0
1
x
положитель
ному
-1
направлению оси ОХ
0 , 5
3
10 х
х

12.

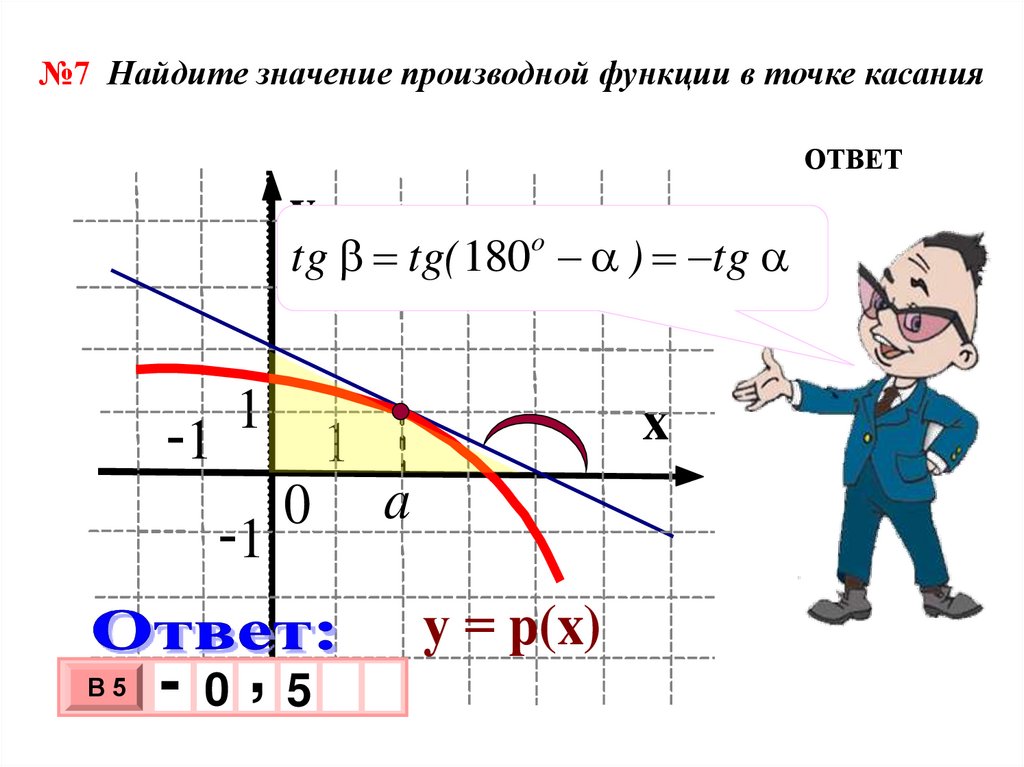
№7 Найдите значение производной функции в точке касания
ОТВЕТ
y
tg tg( 180o ) tg
-1
1
-1
В5
x
1
a
0
-0,5
3
10 х
у = p(x)
х
–
–
Ри

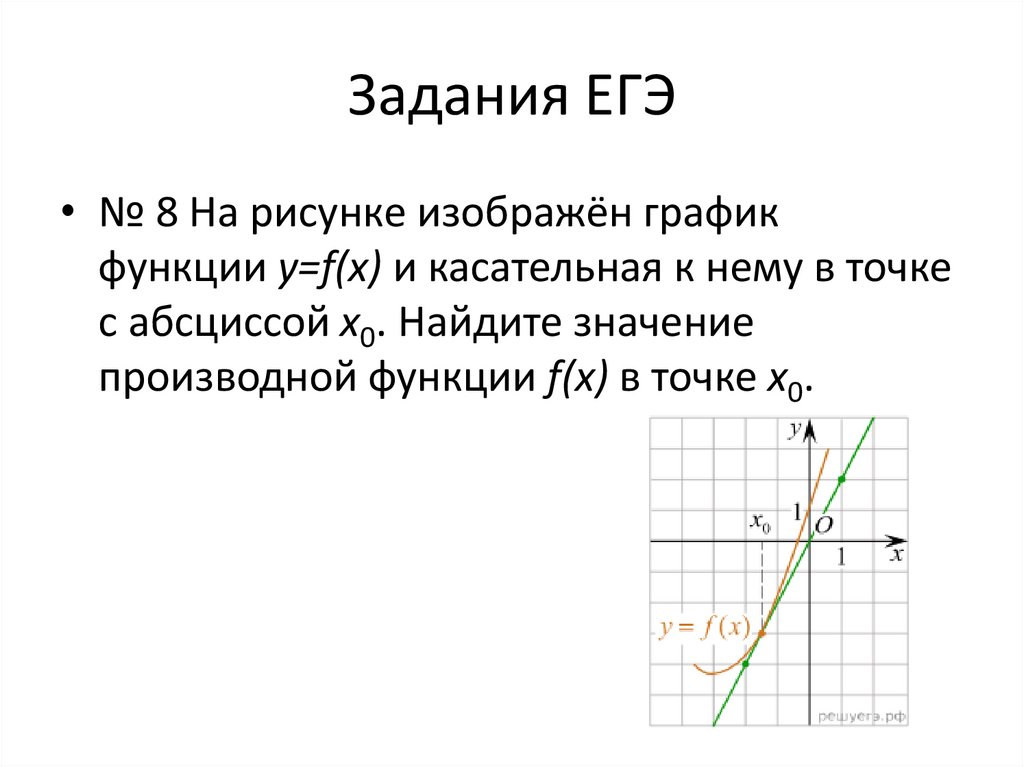
13. Задания ЕГЭ

• № 8 На рисунке изображён график
функции y=f(x) и касательная к нему в точке
с абсциссой x0. Найдите значение
производной функции f(x) в точке x0.

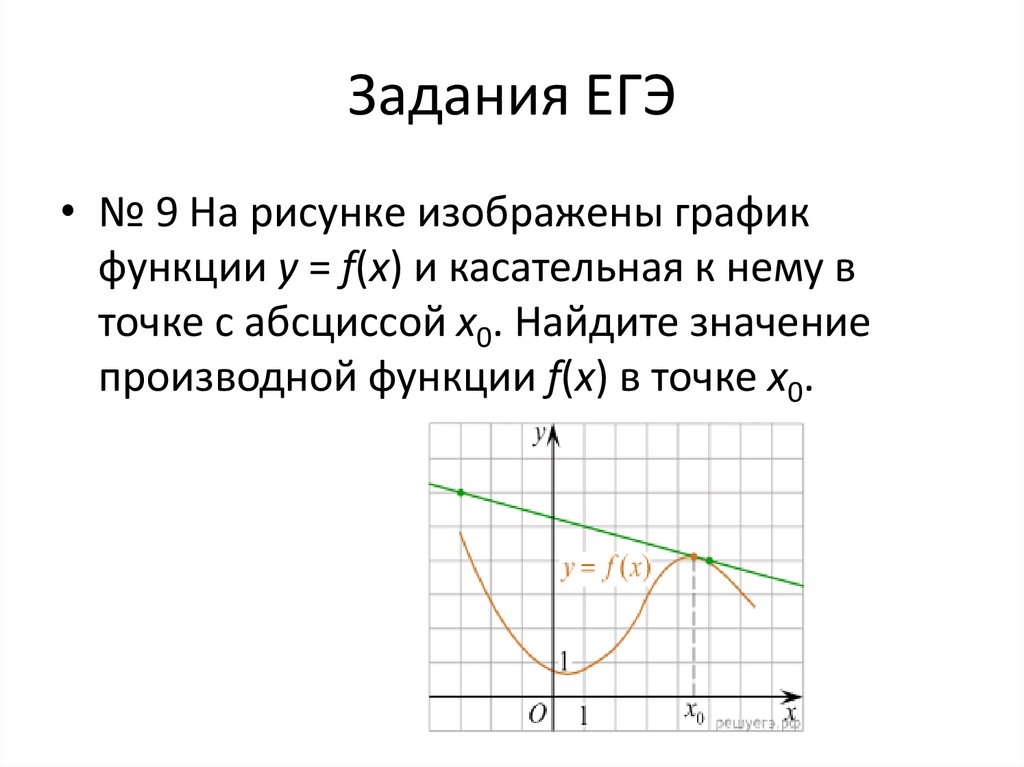
14. Задания ЕГЭ

• № 9 На рисунке изображены график
функции y = f(x) и касательная к нему в
точке с абсциссой x0. Найдите значение
производной функции f(x) в точке x0.

15. Задания ЕГЭ

• № 10На рисунке изображены график
функции y = f(x) и касательная к нему в
точке с абсциссой x0. Найдите значение
производной функции f(x) в точке x0.

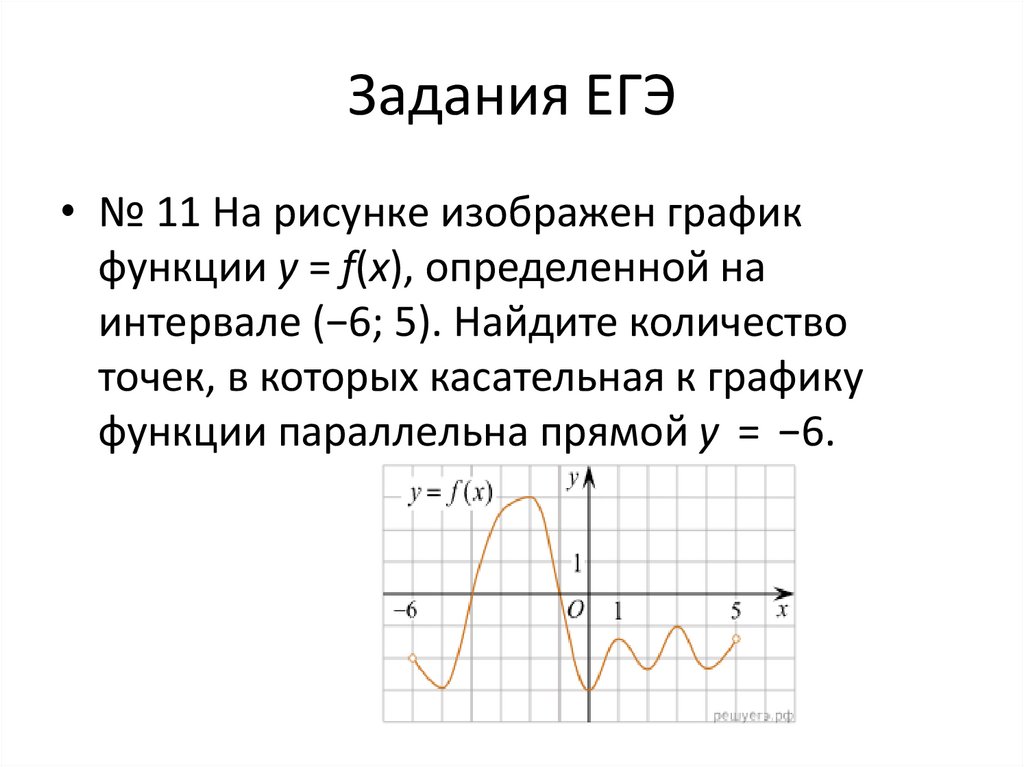
16. Задания ЕГЭ

• № 11 На рисунке изображен график
функции y = f(x), определенной на
интервале (−6; 5). Найдите количество
точек, в которых касательная к графику
функции параллельна прямой y = −6.

17. Задания ЕГЭ

• № 12Прямая
параллельна
касательной к графику функции
• Найдите абсциссу точки касания.

18. Домашнее задание

• 1. Прямая
является касательной
к графику функции
• Найдите абсциссу точки касания.
• 2. На рисунке изображён график
функции y=f(x) и касательная к нему в точке
с абсциссой x0. Найдите значение
производной функции f(x) в точке x0.

19. Домашнее задание

20. Домашнее задание

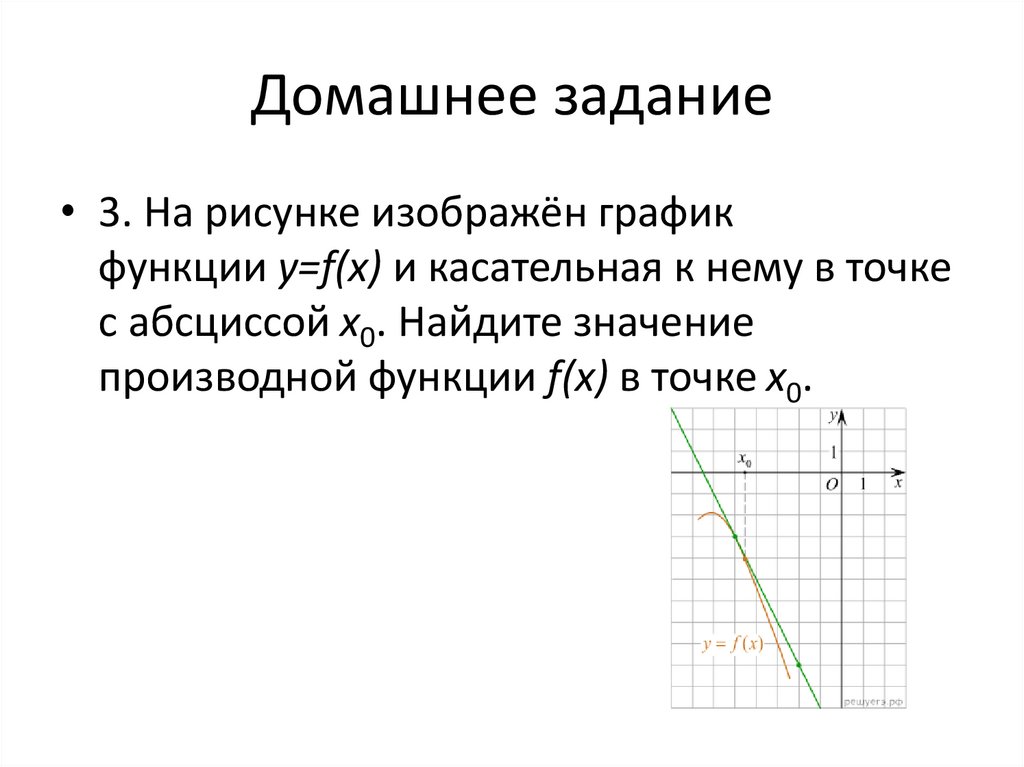
• 3. На рисунке изображён график
функции y=f(x) и касательная к нему в точке
с абсциссой x0. Найдите значение
производной функции f(x) в точке x0.