Similar presentations:
1_2 Определители
1.
§ 2. ОпределителиДля
квадратных
матриц
вводится
числовая
характеристика – определитель (детерминант)
матрицы.
Определитель матрицы A обозначают det A, |A|, DA, A
или .
a11 a12
a21 a22
det A
... ...
an1 an 2
... a1n
... a2 n
.
... ...
... ann
(1)
2.
Вычисление определителейI. Определитель квадратной матрицы 1-го порядка
равен своему элементу: если A = (a11), то det A = a11.
II. Определитель 2-го порядка вычисляется как
произведение элементов, стоящих на главной
диагонали, минус произведение элементов, стоящих на
побочной диагонали:
a11
a12
a21 a22
Пример 1.
1 2
3 4
a11a22 a12 a21.
1 4 2 3 2.
3.
III. Определитель 3-го или более высокого порядкаравен сумме произведений элементов 1-й строки
матрицы на их алгебраические дополнения.
Пусть дан определитель (1) n-го порядка.
Опр. 1. Минор Mij элемента aij – это определитель
(n–1)-го порядка, полученный из определителя (1)
путем вычеркивания i-й строки и j-го столбца, т. е.
строки и столбца, в которых стоит элемент aij.
Опр. 2. Алгебраическим дополнением Aij элемента
aij называется число Aij = (–1)i + jMij.
Определитель (1) n-го порядка вычисляется по
формуле
det A = a11A11 + a12A12 + … + a1nA1n.
4.
В частности, для определителя 3-го порядка имеем:a11 a12
a21 a22
a31 a32
a13
a22
a23 a11
a32
a33
a23
a21 a23
a21 a22
a12
a13
.
a33
a31 a33
a31 a32
5.
В частности, для определителя 3-го порядка имеем:a11 a12
a21 a22
a31 a32
a11
a13
a22
a23 a11
a32
a33
(-1)1+1=(-1)2=1
a23
a21 a23
a21 a22
a12
a13
.
a33
a31 a33
a31 a32
6.
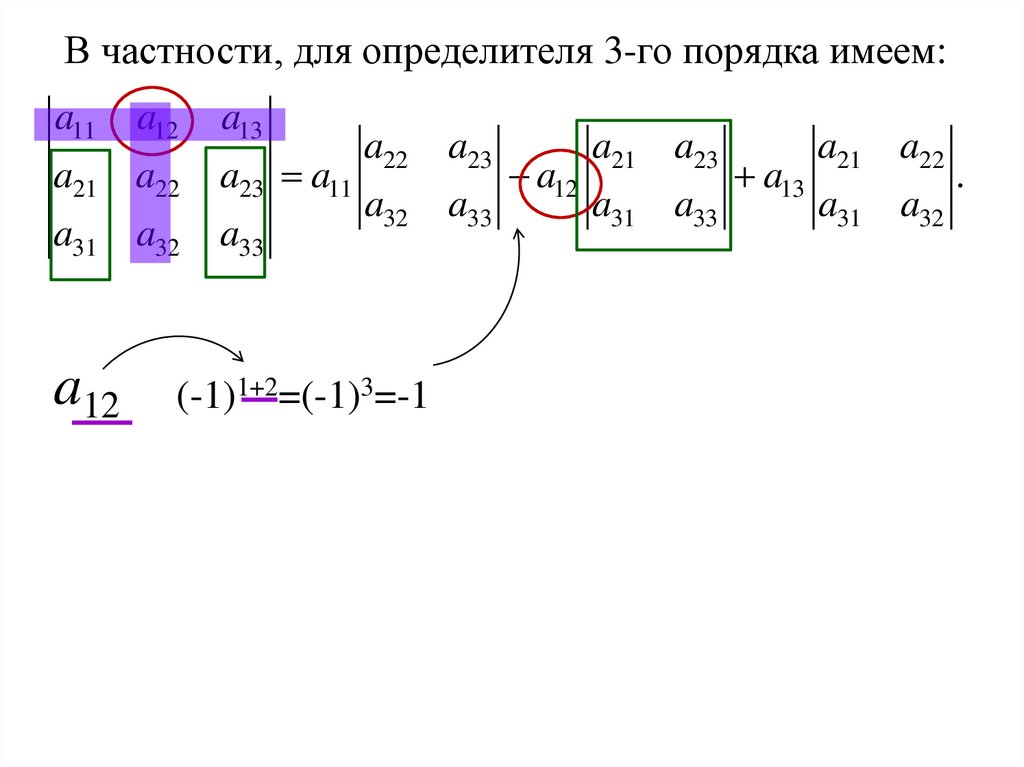
В частности, для определителя 3-го порядка имеем:a11 a12
a21 a22
a31 a32
a12
a13
a22
a23 a11
a32
a33
(-1)1+2=(-1)3=-1
a23
a21 a23
a21 a22
a12
a13
.
a33
a31 a33
a31 a32
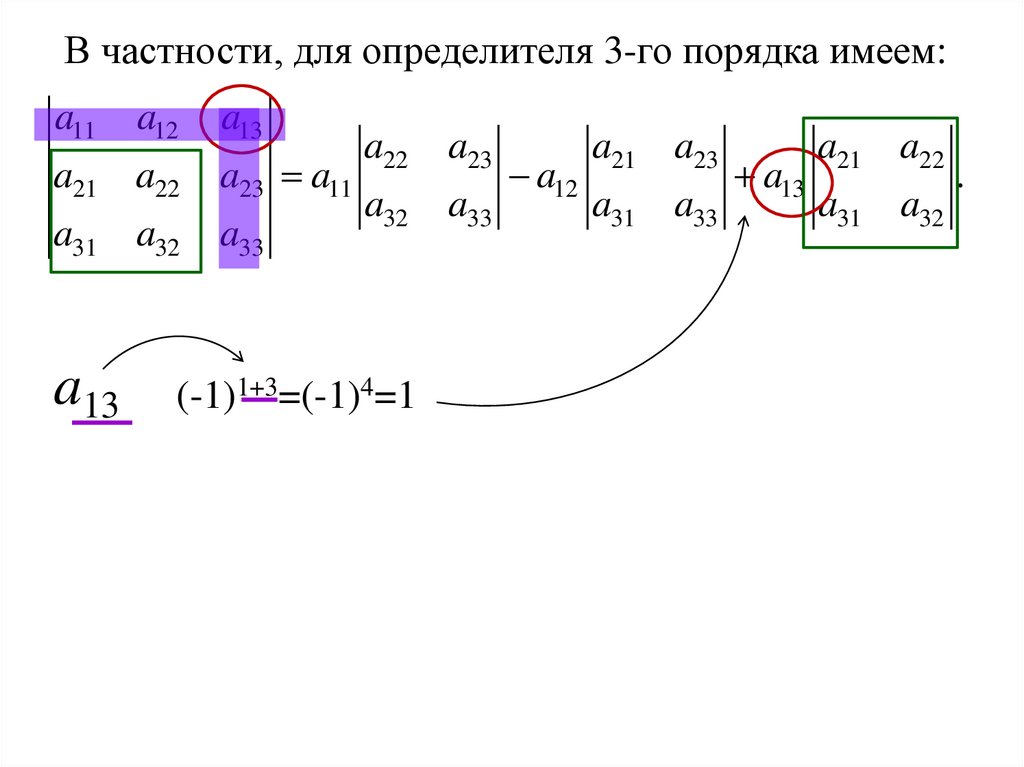
7.
В частности, для определителя 3-го порядка имеем:a11 a12
a21 a22
a31 a32
a13
a13
a22
a23 a11
a32
a33
(-1)1+3=(-1)4=1
a23
a21 a23
a21 a22
a12
a13
.
a33
a31 a33
a31 a32
8.
В частности, для определителя 3-го порядка имеем:a11 a12 a13
a22 a23
a21 a23
a21 a22
a21 a22 a23 a11
a12
a13
.
a32 a33
a31 a33
a31 a32
a31 a32 a33
Правило треугольников (только для определителей 3-го порядка)
a11 a12
a21 a22
a31 a32
!
a13
a23 a11a22a33 a12a23a31 a13a21a32
(a13a22a31 a11a23a32 a12a21a33 )
a33
9.
Правило Саррюса (только для определителей 3-го порядка)a11 a12
a21 a22
a31 a32
!
a13 a11 a12
a23 a21 a22 a11a22a33 a12a23a31 a13a21a32
a33 a31 a32
(a13a22a31 a11a23a32 a12a21a33 )
10.
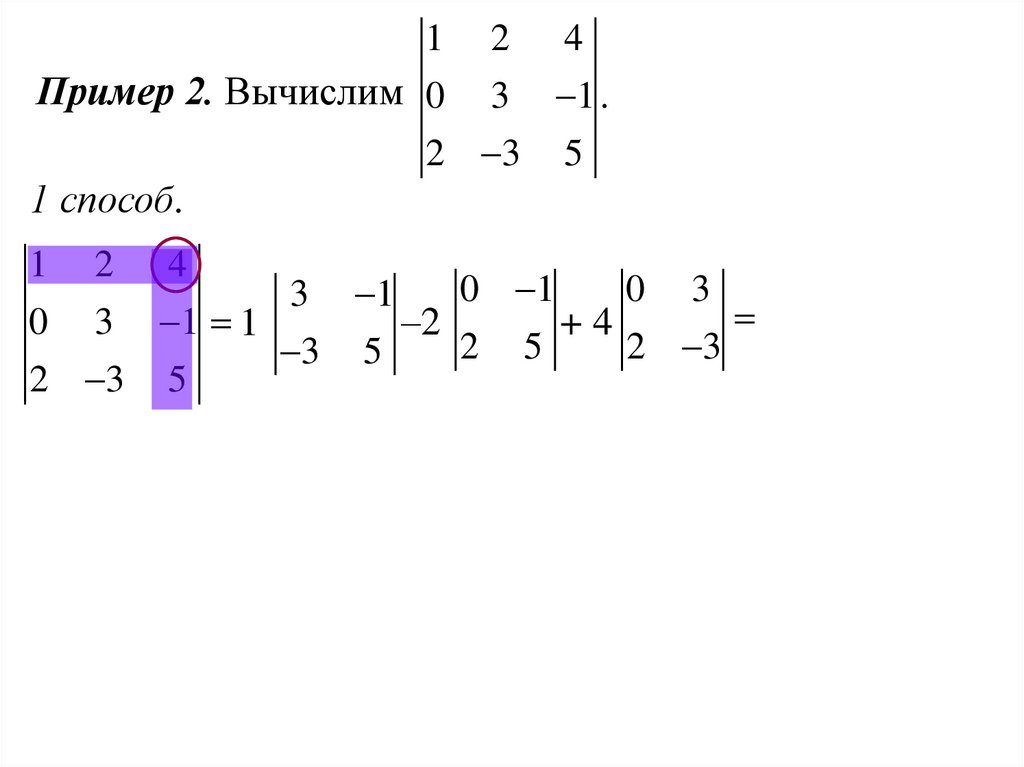
1 2 4Пример 2. Вычислим 0 3 1 .
2 3 5
1 способ.
1 2 4
3 1
0 3 1 1
3 5
2 3 5
11.
1 2 4Пример 2. Вычислим 0 3 1 .
2 3 5
1 способ.
1 2 4
0 1
3 1
0 3 1 1
–2
2 5
3 5
2 3 5
12.
1 2 4Пример 2. Вычислим 0 3 1 .
2 3 5
1 способ.
1 2 4
0 1
0 3
3 1
0 3 1 1
–2
+4
2 5
2 3
3 5
2 3 5
13.
1 2 4Пример 2. Вычислим 0 3 1 .
2 3 5
1 способ.
1 2 4
0 1
0 3
3 1
0 3 1 1
–2
+4
2 5
2 3
3 5
2 3 5
1 (15 3) 2 (0 2) 4 (0 6) 12 4 24 16.
2 способ.
1 2 4
0 3 1 1 3 5 2 ( 1) 2 4 0 ( 3)
2 3 5
14.
1 2 4Пример 2. Вычислим 0 3 1 .
2 3 5
1 способ.
1 2 4
0 1
0 3
3 1
0 3 1 1
–2
+4
2 5
2 3
3 5
2 3 5
1 (15 3) 2 (0 2) 4 (0 6) 12 4 24 16.
2 способ.
1 2 4
0 3 1 1 3 5 2 ( 1) 2 4 0 ( 3) (4 3 2
2 3 5
1 ( 1) ( 3) 2 0 5) 15 4 0 (24 3 0) 16.
15.
1 2 4Пример 2. Вычислим 0 3 1 .
2 3 5
3 способ.
1 2 4 1 2
0 3 1 0 3 1 3 5 2 ( 1) 2 4 0 ( 3) (4 3 2
2 3 5 2 3
1 ( 1) ( 3) 2 0 5) 15 4 0 (24 3 0) 16.
2 способ.
1 2 4
0 3 1 1 3 5 2 ( 1) 2 4 0 ( 3) (4 3 2
2 3 5
1 ( 1) ( 3) 2 0 5) 15 4 0 (24 3 0) 16.
16.
Свойства определителей1. При транспонировании матрицы определитель не
изменяется: det A = det AT.
Следствие.
Все
свойства
определителей,
сформулированные для строк, справедливы и для
столбцов.
2. При перестановке двух строк определитель меняет
знак.
3. Если у определителя какая-либо строка состоит
только из нулей, то такой определитель равен 0.
4. Определитель, содержащий две одинаковые
строки, равен 0.
5. Общий множитель элементов строки можно
вынести за знак определителя.
17.
6. Если к элементам какой-либо строки прибавитьсоответствующие элементы другой строки, умноженные
на одно и то же число, то определитель не изменится.
7 (теорема Лапласа). Определитель равен сумме
произведений элементов любой строки на их
алгебраические дополнения:
det A ai1 Ai1 ai 2 Ai 2 ... ain Ain (1 i n).
18.
19.
6. Если к элементам какой-либо строки прибавитьсоответствующие элементы другой строки, умноженные
на одно и то же число, то определитель не изменится.
7 (теорема Лапласа). Определитель равен сумме
произведений элементов любой строки на их
алгебраические дополнения:
det A ai1 Ai1 ai 2 Ai 2 ... ain Ain (1 i n).
8 («фальшивое разложение»). Сумма произведений
элементов какой-либо строки на алгебраические
дополнения соответствующих им элементов другой
строки равна 0:
ai1 Ak1 ai 2 Ak 2 ... ain Akn 0 (1 i, k n, i k ).
20.
9. Сумма произведений алгебраических дополненийэлементов какой-либо строки определителя на
некоторые числа b1, b2, …, bn равна определителю,
который получается из данного заменой указанной
строки на числа b1, b2, …, bn.
2 12345 56789
Пример 3. Вычислим 0
3
13579 .
0
0
5
2 12345 56789
3 13579
0
3
13579 2
2 3 ( 5) 30.
0
5
0
0
5
21.
9. Сумма произведений алгебраических дополненийэлементов какой-либо строки определителя на
некоторые числа b1, b2, …, bn равна определителю,
который получается из данного заменой указанной
строки на числа b1, b2, …, bn.
10. Определитель матрицы, у которой все элементы
под главной диагональю равны 0 (треугольной
матрицы), равен произведению элементов, стоящих на
главной диагонали.
Упражнение 1. Чему равен определитель матрицы с
нулями под побочной диагональю?
Упражнение 2. Проверить свойства на примере
определителей 2-го порядка.
Упражнение 3. Доказать свойства 3–10.
22.
Пример 4. Вычислим определитель, преобразовав егок треугольному виду.
×(–2)
1
2
4
1 2 4
3
1
0 3 1 0
2 2 1 3 2 2 5 2 4
2 3 5
1 2 4
1 4 2
1
4
2
×(–3)
1
3
0 3 1
0 1 3 0
0 3 3 ( 1) 7 3 3
0 7 3
0 3 7
1 4
2
0 1 3 (1 ( 1) ( 16)) 16
0 0 16
23.
Тh 1. Определитель произведения квадратныхматриц равен произведению их определителей:
det( AB) det A det B.









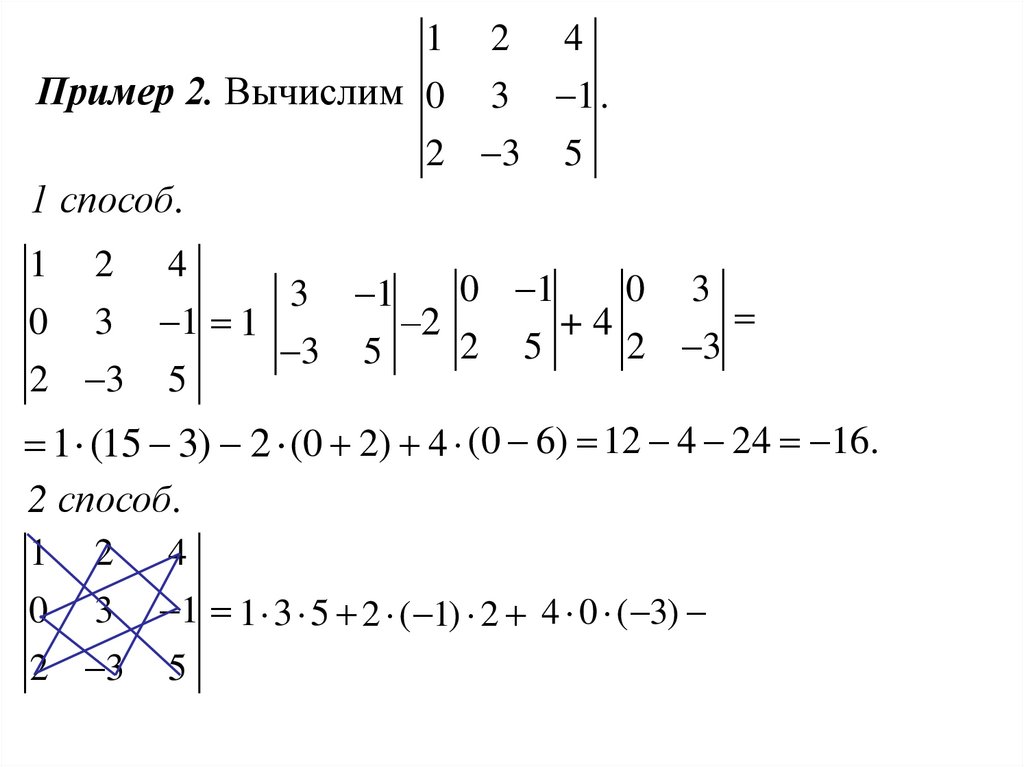










 mathematics
mathematics








