Similar presentations:
3_4 Опред инт24
1.
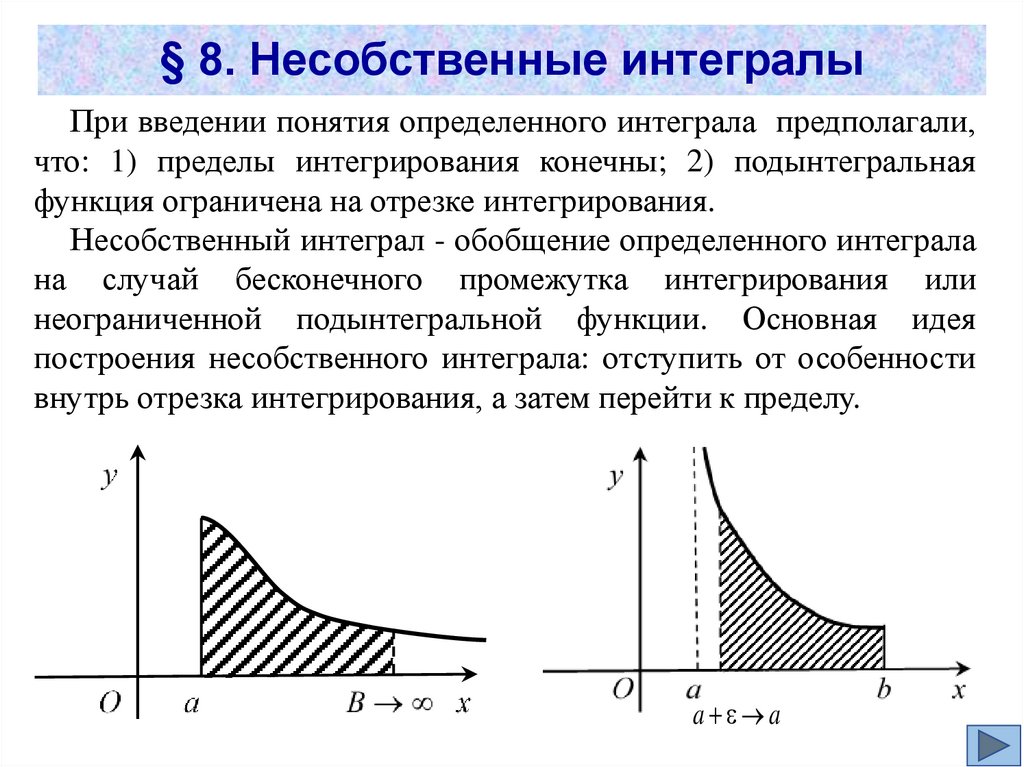
§ 8. Несобственные интегралыПри введении понятия определенного интеграла предполагали,
что: 1) пределы интегрирования конечны; 2) подынтегральная
функция ограничена на отрезке интегрирования.
Несобственный интеграл - обобщение определенного интеграла
на случай бесконечного промежутка интегрирования или
неограниченной подынтегральной функции. Основная идея
построения несобственного интеграла: отступить от особенности
внутрь отрезка интегрирования, а затем перейти к пределу.
a a
2.
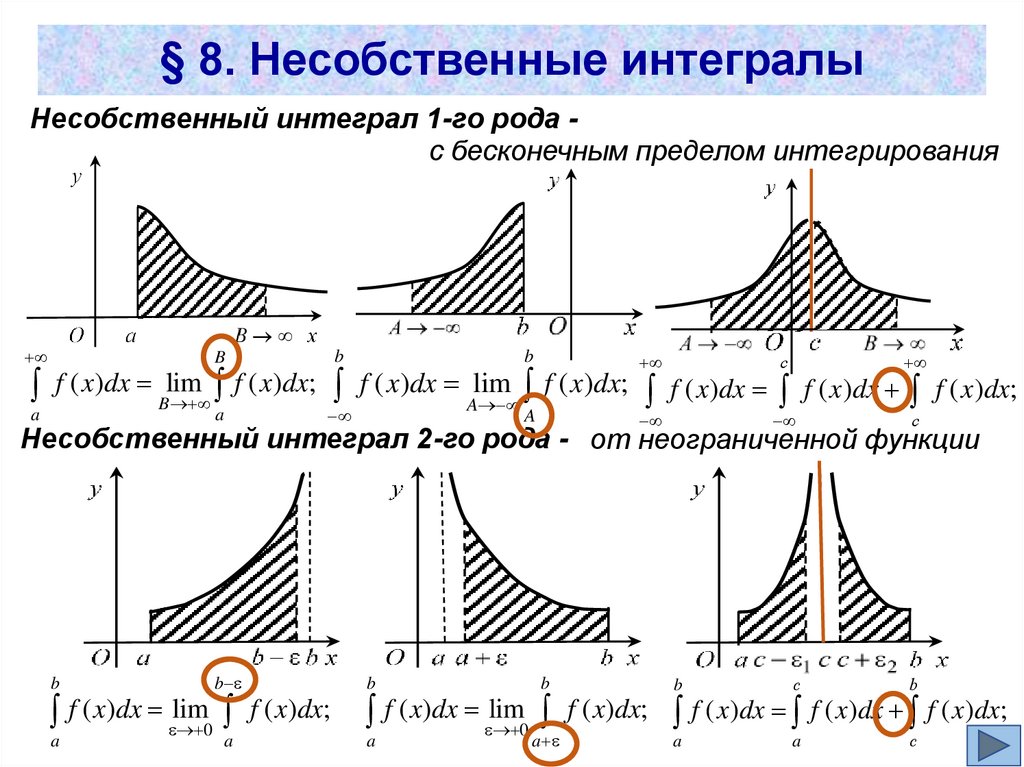
Несобственные интегралы с бесконечными пределамиинтегрирования (несобственные интегралы 1-го рода)
Опр. 1. Пусть функция f ( x) интегрируема на любом отрезке
[a; B], где B a. Несобственным интегралом с бесконечным
верхним пределом называется предел
B
a
a
f ( x)dx Blim
f ( x)dx;
причем
если
этот
предел
существует
и
конечен,
то
несобственный
интеграл
называется
сходящимся,
в
противном случае – расходящимся.
Пример 1.
B
dx lim dx lim ln | x | B lim (ln B 0) ,
1
B
x B 1 x B
1
т. е. несобственный интеграл расходится.
3.
dxПример 2. Исследуем сходимость при 1.
1 x
B
B
1 B
dx
dx
x
lim x dx lim
x Blim
x
B
B 1
1
1
1
1
B 1
1
1
1
lim
lim
1
1
B 1
1 1 B B
1
, если 1, - сходится
1
- расходится
, если 1.
dx сходится, если 1,
x расходится, если 1.
1
(1)
4.
Опр. 2. Если функция f ( x) интегрируема на любом отрезке[ A; b], где A b, то несобственным интегралом с бесконечным
нижним пределом называется предел
b
b
A
f ( x )dx;
f ( x)dx Alim
причем если предел существует и конечен, то несобственный
интеграл называется сходящимся, в противном случае –
расходящимся.
Опр. 3. Несобственный интеграл с двумя бесконечными
пределами интегрирования определяется как сумма
с
с
f ( x)dx f ( x)dx f ( x)dx;
Замечание. Доказано, что это определение не зависит от
выбора промежуточной точки c.
!
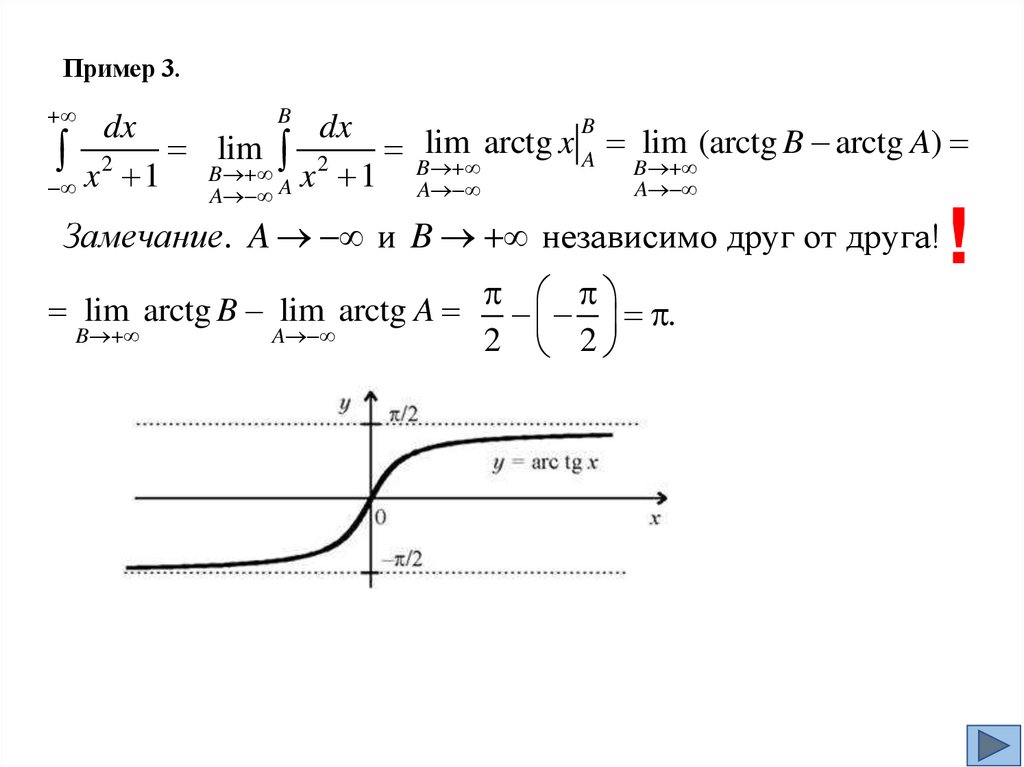
5.
Пример 3.B
B
dx
dx
arctg x A lim (arctg B arctg A)
Blim
x2 1 Blim
2
B
x 1
A
A
A A
Замечание. A и B независимо друг от друга!
lim arctg B lim arctg A
B
A
.
2 2
!
6.
В некоторых случаях для интегралаf ( x )dx, который расходится,
рассматривают его сходимость в смысле главного значения
A
v.p. f ( x)dx lim f ( x)dx.
A
A
Обратное утверждение неверно.
Если несобственный интеграл расходится, то в смысле главного
значения он может как сходиться, так и расходиться.
Пример 4. 1) v.p. sin xdx
xdx
2
x
1
2
x dx
3) v.p. 2
x 1
2) v.p.
сходится
сходится
расходится
Упражнение 1. Показать, что
несобственные интегралы
xdx x 2 dx
sin xdx; x 2 1; x 2 1
расходятся.
7.
Признаки сравнения несобственных интегралов 1-го родаТ 1. Пусть функции f ( x) и g ( x) интегрируемы на любом
конечном промежутке, содержащемся в [a; ), и 0 f ( x) g( x)
при всех x [a; ). Тогда:
a
a
– если g ( x)dx сходится ⇒ f ( x)dx сходится;
– если f ( x)dx расходится ⇒ g ( x)dx расходится.
a
a
dx
Пример 5. Исследуем сходимость интеграла 4
.
1 x 4
1
1
dx
dx
0 4
4 0 4
4.
x 4 x
1 x 4
1 x
1
.
Упражнение 2. Найти первообразную для 4
x 4
8.
Т 2. Пусть функции f ( x) и g ( x) интегрируемы на любомконечном промежутке, содержащемся в [a; ); f ( x ) 0, g ( x ) 0
при всех x [a; ) и существует конечный, отличный от 0 предел
f ( x)
lim
A ( A 0, ). Тогда несобственные интегралы
x g ( x )
a
a
f ( x)dx и g ( x)dx ведут себя в смысле сходимости одинаково,
т. е. либо оба сходятся, либо оба расходятся.
Т 3. Если
a
a
f ( x ) dx сходится, то и f ( x)dx сходится. (В этом
случае интеграл f ( x)dx называется абсолютно сходящимся.)
Замечание 1.a Для сравнения обычно используются
интегралы вида (1).
Замечание 2. Аналогичные признаки сравнения верны и
для несобственных интегралов по другим бесконечным
промежуткам.
9.
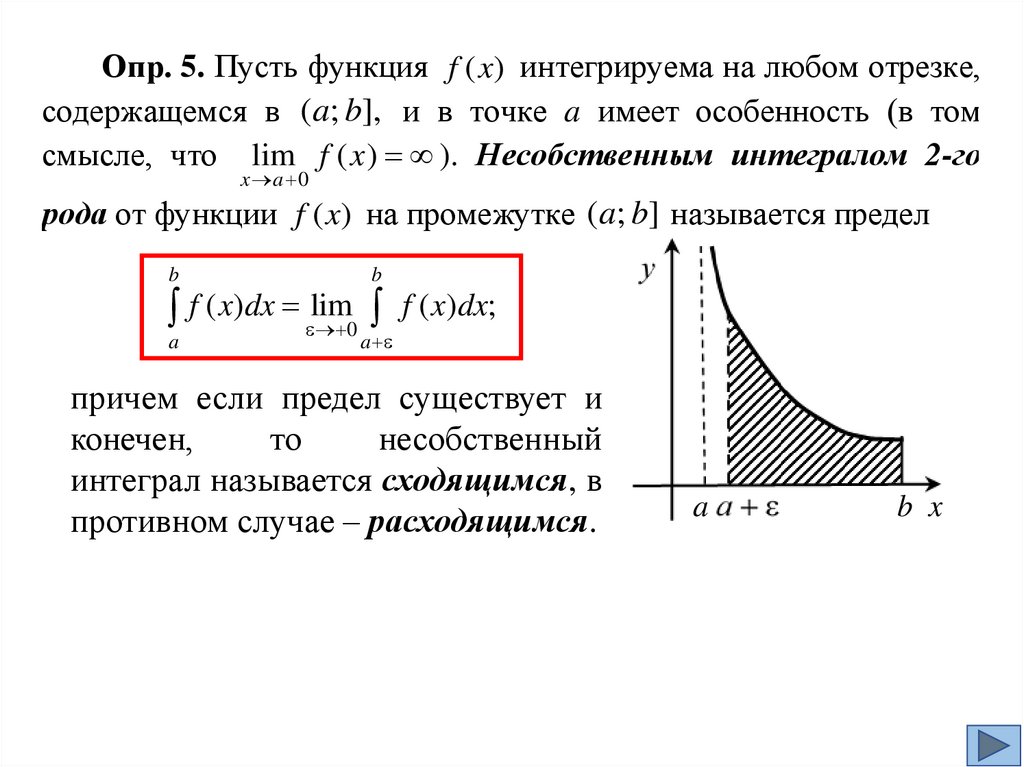
Несобственные интегралы от неограниченных функций(несобственные интегралы 2-го рода)
Пусть функция f (x) интегрируема на
любом отрезке, содержащемся в [a; b), и
lim
f ( x ) (функция не ограничена в
.
x b 0
окрестности точки b). В этом случае
говорят, что функция f (x)
имеет
особенность в точке x = b, а саму точку
x = b называют особой точкой.
a
b x
Опр. 4. Пусть функция f (x) интегрируема на любом отрезке,
содержащемся в [a; b), и в точке b имеет особенность.
Несобственным интегралом 2-го рода от функции f (x) на
промежутке [a; b) называется предел
b
b
a
a
lim f ( x)dx;
f ( x)dx
0
причем если предел существует и конечен, то несобственный
интеграл называется сходящимся, в противном случае –
расходящимся.
10.
Опр. 5. Пусть функция f ( x) интегрируема на любом отрезке,содержащемся в (a; b], и в точке a имеет особенность (в том
смысле, что lim f ( x ) ). Несобственным интегралом 2-го
x a 0
рода от функции f ( x) на промежутке (a; b] называется предел
b
b
a
a
lim f ( x)dx;
f ( x)dx
0
причем если предел существует и
конечен,
то
несобственный
интеграл называется сходящимся, в
противном случае – расходящимся.
a
b x
11.
Пример 6.4
4
dx
1
dx
lim
lim
2
( x 4)2
0
0 x 4
0 ( x 4)
0
0
4
1
1
lim
0 4 4
4
1 1
lim ⇒ расходится.
0
4
Упражнение 3. Показать, что
расходится, если 1,
dx
(b x ) сходится, если 1.
a
b
(2)
Сравнить с (1).
Упражнение 4. Показать, что
расходится, если 1,
dx
( x a ) сходится, если 1.
a
b
Сравнить с (1) и (2).
(3)
12.
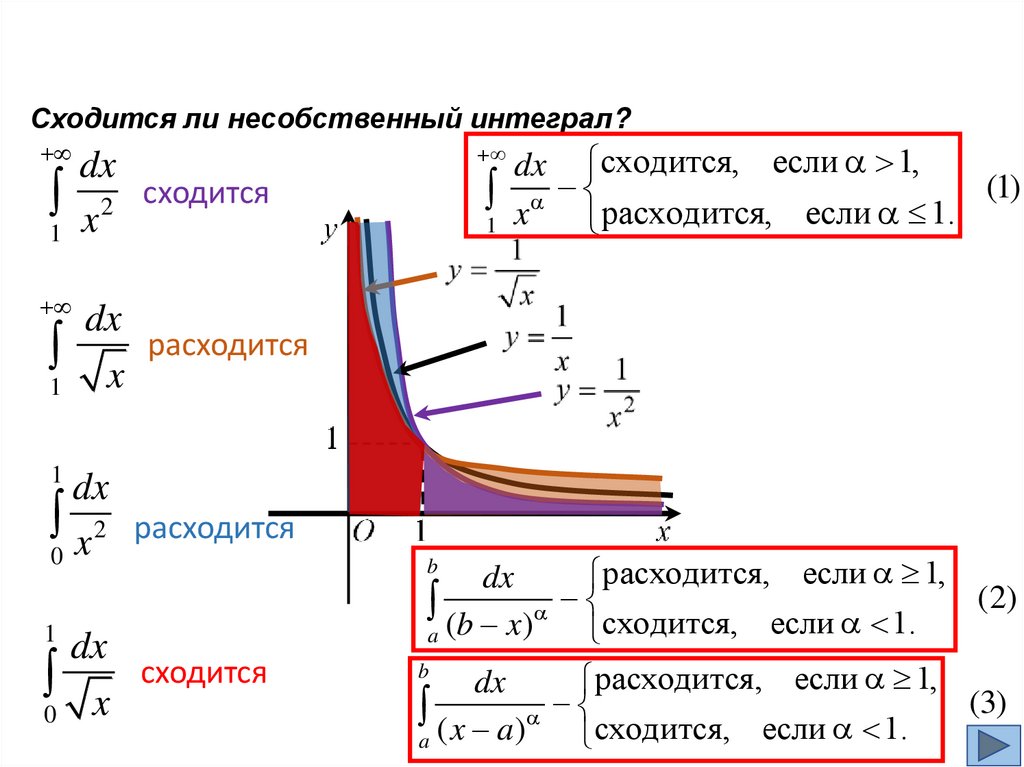
Сходится ли несобственный интеграл?dx сходится, если 1,
x расходится, если 1. (1)
1
dx
x 2 сходится
1
dx
x расходится
1
1
dx
x 2 расходится
0
1
dx
x сходится
0
расходится, если 1,
dx
(b x) сходится, если 1. (2)
a
b
расходится, если 1,
dx
( x a) сходится, если 1. (3)
a
b
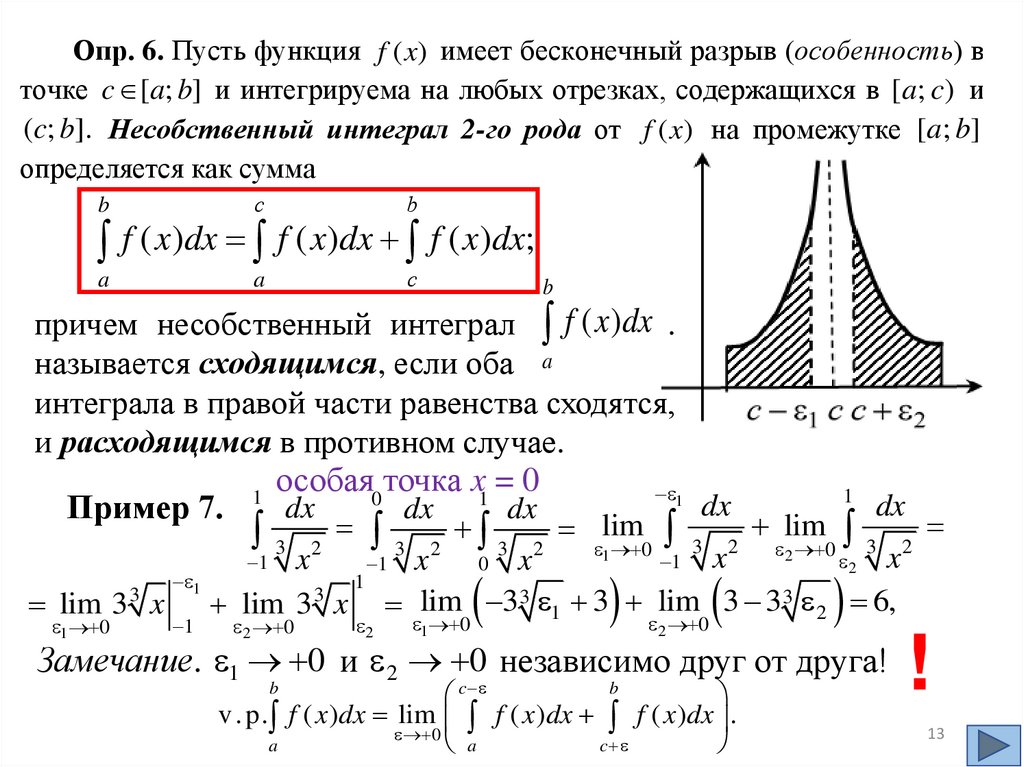
13.
Опр. 6. Пусть функция f ( x) имеет бесконечный разрыв (особенность) вточке c [a; b] и интегрируема на любых отрезках, содержащихся в [a; c) и
(c; b]. Несобственный интеграл 2-го рода от f ( x) на промежутке [a; b]
определяется как сумма
b
с
b
a
a
с
f ( x)dx f ( x)dx f ( x)dx;
b
причем несобственный интеграл f ( x )dx .
называется сходящимся, если оба a
интеграла в правой части равенства сходятся,
и расходящимся в противном случае.
особая0 точка x1 = 0
1
1
1
dx
dx
dx
Пример 7.
dx
dx
3 2 lim
3 2 3 2 3 2 1lim
3
2
0
0
2
x
1
2 x
1 x
1 x
0 x
lim 3 x
3
1 0
1
1
lim 3 x
3
2 0
1
2
lim 3 3 1 3 lim 3 3 3 2 6,
1 0
2 0
Замечание. 1 0 и 2 0 независимо друг от друга!
b
c
v . p. f ( x )dx lim f ( x )dx f ( x )dx .
0
a
c
a
b
!
13
14.
§ 8. Несобственные интегралыНесобственный интеграл 1-го рода с бесконечным пределом интегрирования
B
b
b
с
a
a
A
с
f ( x )dx; f ( x )dx lim f ( x )dx; f ( x )dx f ( x )dx f ( x )dx;
f ( x)dx Blim
A
Несобственный интеграл 2-го рода - от неограниченной функции
b
b
a
a
lim f ( x)dx;
f ( x)dx
0
b
b
b
с
b
a
a
a
a
с
lim f ( x)dx; f ( x )dx f ( x )dx f ( x )dx;
f ( x)dx
0
15.
Признаки сравнения для несобственных интегралов 2-го родаформулируются
аналогично
признакам
сравнения
для
несобственных интегралов 1-го рода.
Т 4. Пусть функции f ( x) и g ( x) интегрируемы на любом
конечном промежутке, содержащемся в [a; b), и 0 f ( x) g( x)
при всех x [a; b). Тогда:
b
b
a
b
a
– если g ( x )dx сходится ⇒ f ( x)dx сходится;
b
– если f ( x)dx расходится ⇒ g ( x )dx расходится.
a
a
Упражнение 5. Сформулировать предельный признак
сравнения несобственных интегралов 2-го рода аналогично
теореме 2.
16.
§ 9. Геометрические приложенияопределенного интеграла
Теорема
(алгоритм применения определённого интеграла)
Если величина Q обладает на промежутке [a,b]
1.свойством аддитивности, а именно,
если a = x0 x1 x2 … xn = b,
то Q= Q1+ Q2+…+ Qn, где Qi – значение Q на [xi -1,xi],
i=1,2,…n;
2. свойством линейности Q в малом: Q f(x) x, где f(x) –
интегрируемая на [a,b] функция,
то величину Q можно найти интегралом от её элемента
dQ = f(x)dx по промежутку [a,b]:
b
Q f ( x)dx
a
17.
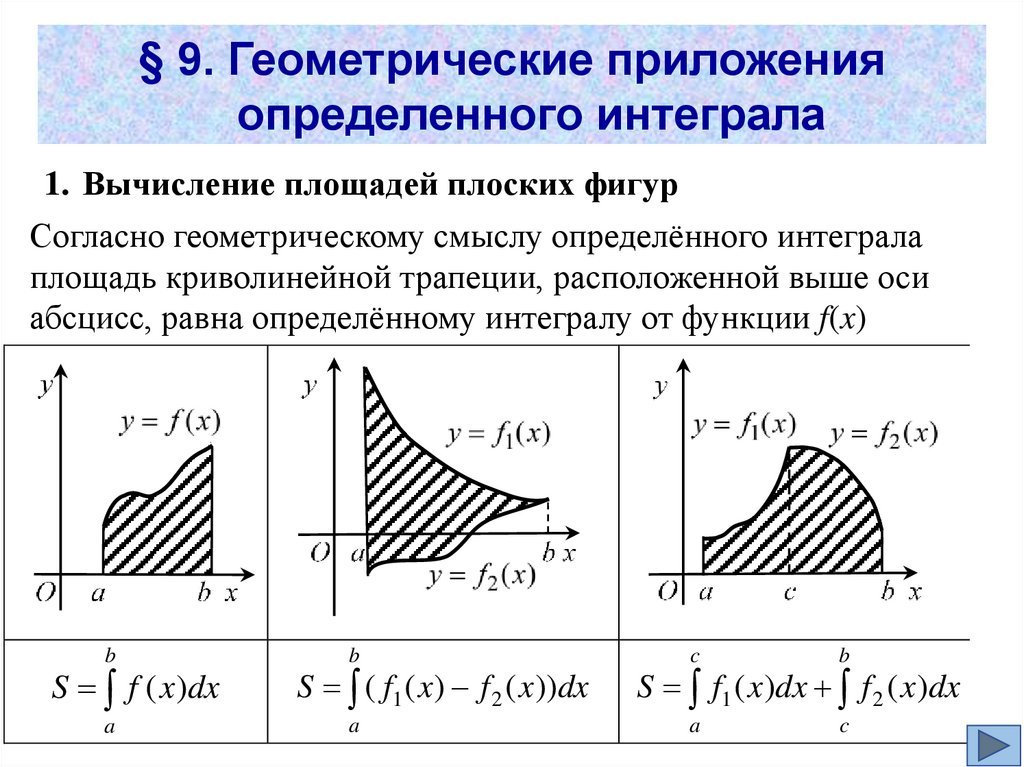
§ 9. Геометрические приложенияопределенного интеграла
1. Вычисление площадей плоских фигур
Согласно геометрическому смыслу определённого интеграла
площадь криволинейной трапеции, расположенной выше оси
абсцисс, равна определённому интегралу от функции f(x)
b
S f ( x )dx
a
b
S ( f1 ( x ) f 2 ( x ))dx
a
c
b
a
c
S f1 ( x )dx f 2 ( x )dx
18.
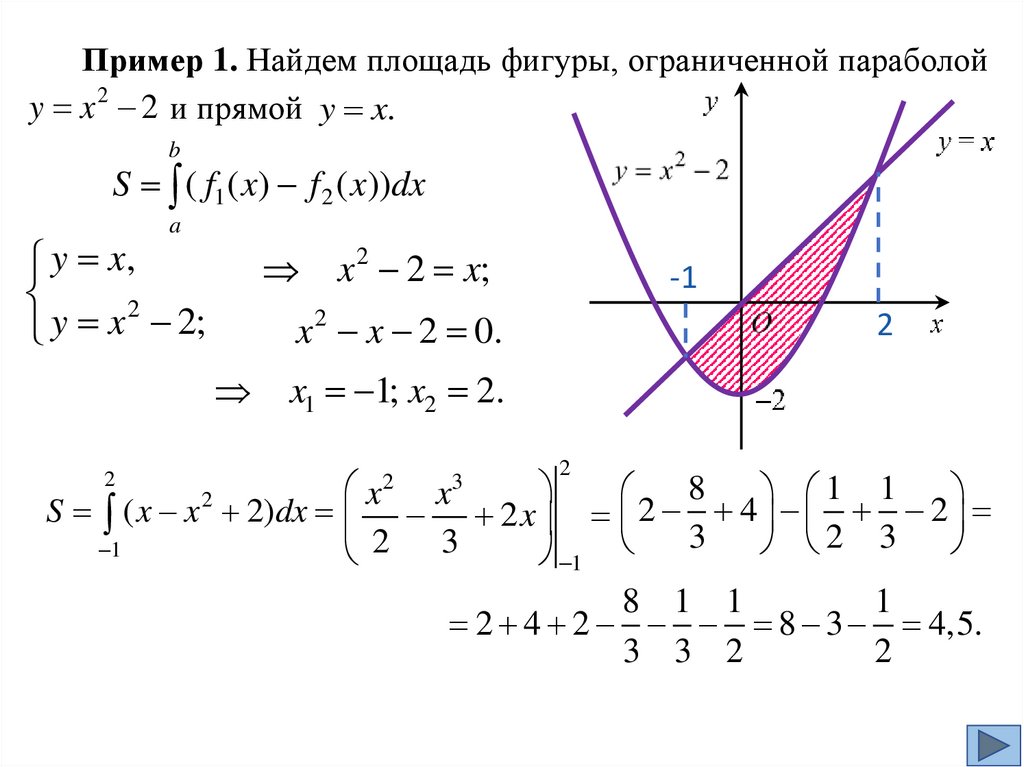
Пример 1. Найдем площадь фигуры, ограниченной параболойy x 2 2 и прямой y x.
b
S ( f1 ( x) f 2 ( x))dx
a
y x,
2
y
x
2;
x 2 2 x;
-1
x 2 x 2 0.
2
x1 1; x2 2.
2
8
x
1 1
x
S ( x x 2)dx 2 x 2 4 2
3
2 3
1
2 3
1
8 1 1
1
2 4 2 8 3 4,5.
3 3 2
2
2
2
2
3
19.
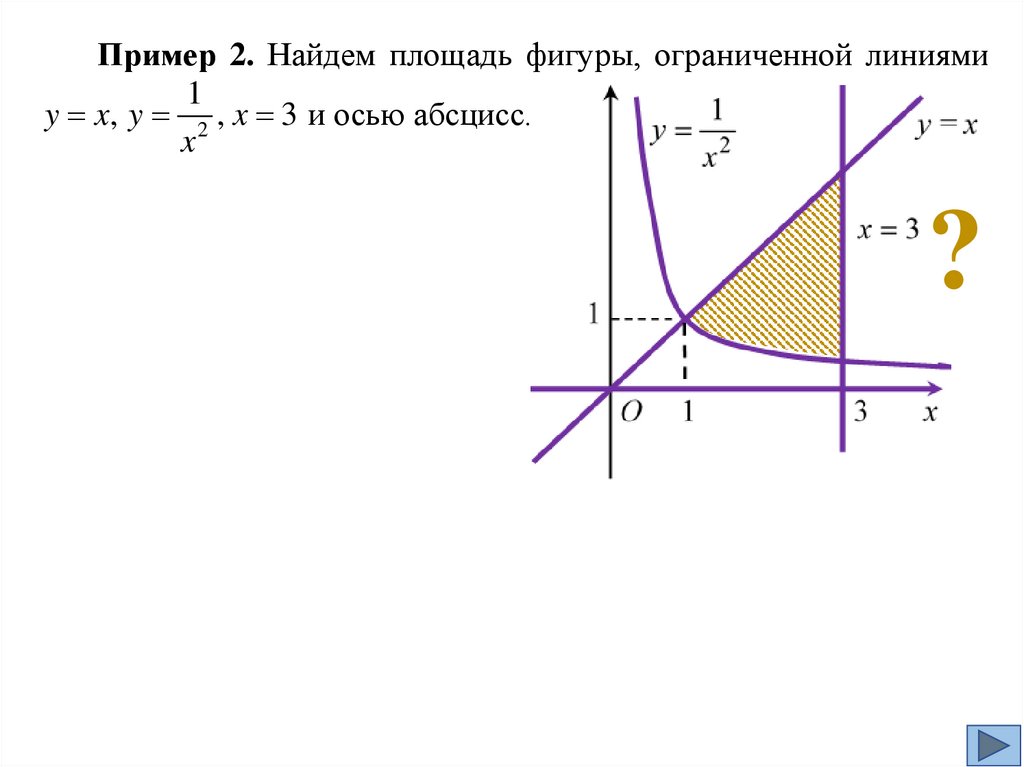
Пример 2. Найдем площадь фигуры, ограниченной линиями1
y x, y 2 , x 3 и осью абсцисс.
x
?
20.
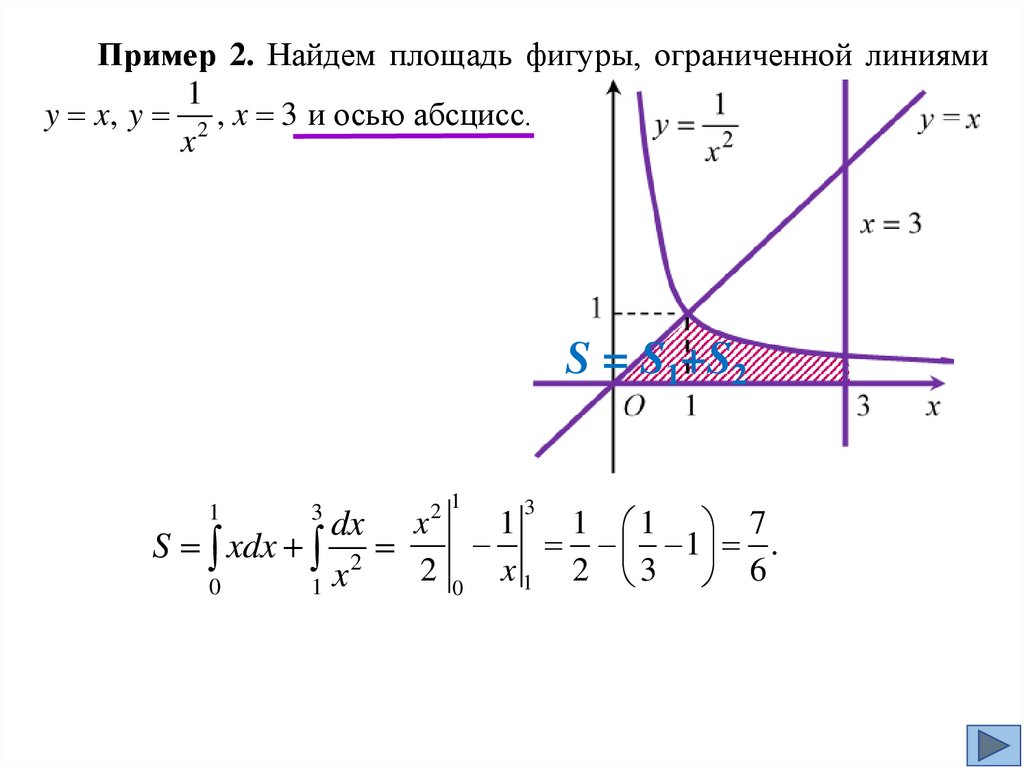
Пример 2. Найдем площадь фигуры, ограниченной линиями1
y x, y 2 , x 3 и осью абсцисс.
x
S = S1+S2
2 1
3
1
1 1 7
dx x
1 .
S xdx 2
2 0 x1 2 3 6
0
1 x
1
3
21.
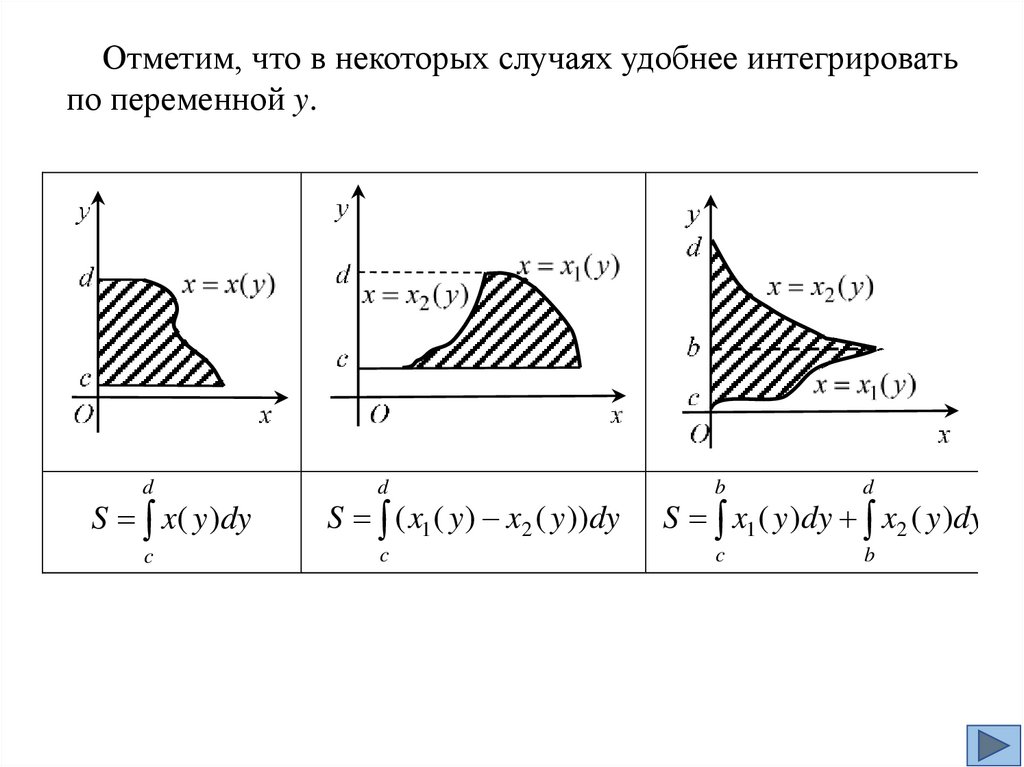
Отметим, что в некоторых случаях удобнее интегрироватьпо переменной y.
d
S x( y )dy
c
d
S ( x1 ( y ) x2 ( y ))dy
c
b
d
c
b
S x1 ( y )dy x2 ( y )dy
22.
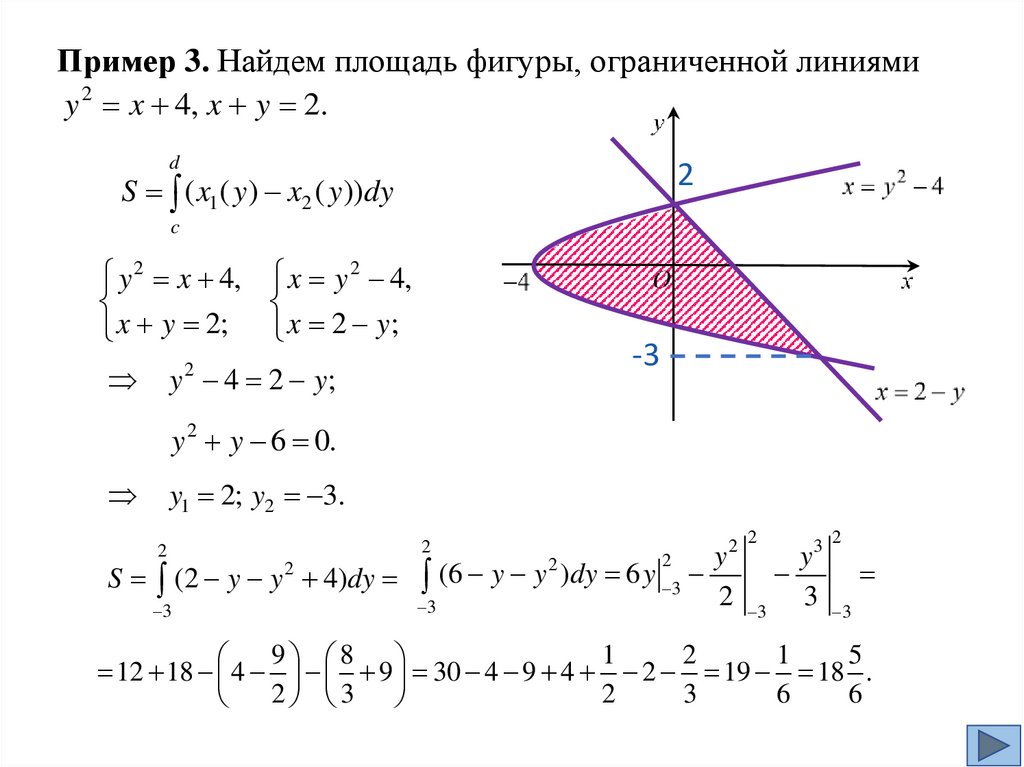
Пример 3. Найдем площадь фигуры, ограниченной линиямиy 2 x 4, x y 2.
d
2
S ( x1 ( y ) x2 ( y ))dy
c
y 2 x 4, x y 2 4,
x
y
2;
x 2 y;
-3
y 4 2 y;
2
y 2 y 6 0.
y1 2; y2 3.
2
2
2
2
S (2 y y 4)dy (6 y y )dy 6 y 3
2
3
3
2 2
3 2
y
y
2 3 3 3
9 8
1
2
1
5
12 18 4 9 30 4 9 4 2 19 18 .
2 3
2
3
6
6
23.
Если криволинейная трапеция на отрезке[a; b] ограничена снизу осью Ox (прилежит
к оси Ox), а сверху линией, заданной
параметрически:
x x (t ),
y y (t ),
b
то, выполнив замену в интеграле Sкр. трап. f ( x )dx, получим
a
следующую формулу:
t2
Sкр.трап y (t ) x (t )dt,
t1
где x (t1 ) a; x (t2 ) b.
!
24.
Пример 4. Найдемx a cos t ,
0 t 2 .
y b sin t ,
площадь,
ограниченную
эллипсом
Sэл = πab
x 0, a cos t 0, cos t 0,
t
;
1
2
y b; b sin t b; sin t 1;
x a, a cos t a, cos t 1,
t2 0.
y 0; b sin t 0; sin t 0;
x=a
x=0
a
0
0
0
0
2
2
2
S 4 y ( x)dx 4 y (t ) x (t )dt 4 b sin t ( a sin t )dt 4ab sin tdt
2 1 cos 2t
4ab
0
2
2
2
2
2
1
dt 2ab dt cos 2tdt 2ab t 02 sin 2t
2
0
0
0
1
2ab (sin sin 0) ab.
2 2
!
25.
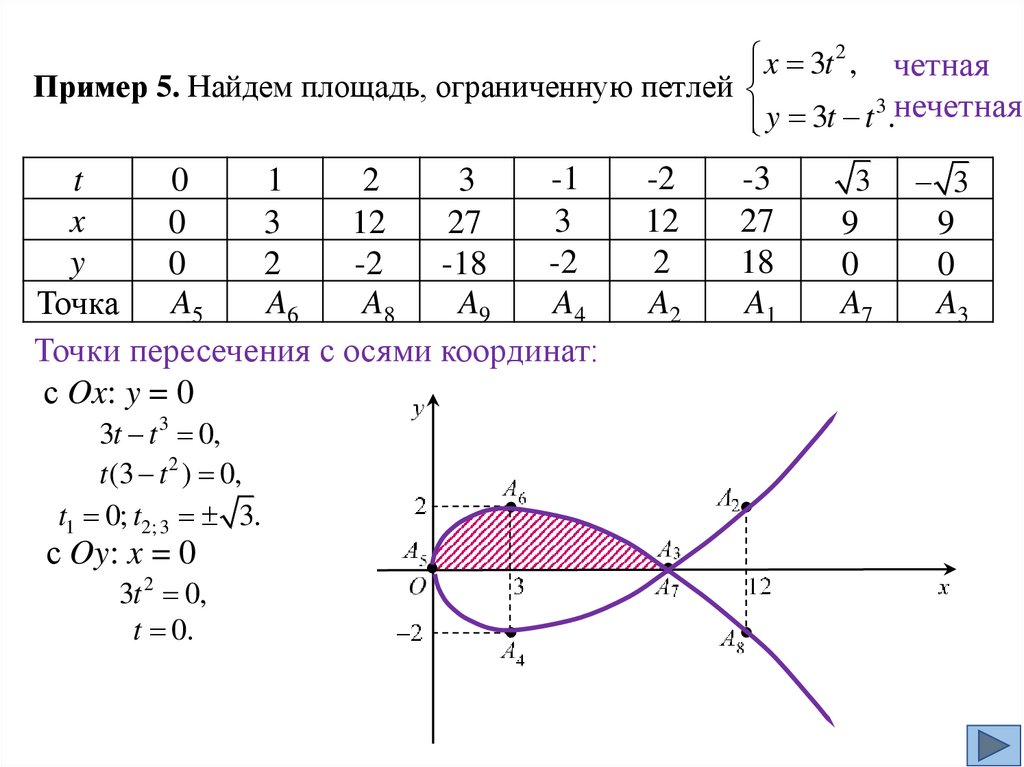
x 3t 2 , четнаяПример 5. Найдем площадь, ограниченную петлей
3
y 3t t .нечетная
-1
t
0
1
2
3
x
3
0
3
12
27
y
-2
0
2
-2
-18
A5
A6
A8
A9
A4
Точка
Точки пересечения с осями координат:
с Ox: y = 0
3t t 3 0,
t (3 t 2 ) 0,
t1 0; t2; 3 3.
с Oy: x = 0
3t 2 0,
t 0.
-2
12
2
A2
-3
27
18
A1
3
3
9
0
A7
9
0
A3
26.
x 3t 2 , четнаяПример 5. Найдем площадь, ограниченную петлей
3
y 3t t .нечетная
-1
t
0
1
2
3
x
3
0
3
12
27
y
-2
0
2
-2
-18
A5
A6
A8
A9
A4
Точка
Точки пересечения с осями координат:
с Ox: y = 0
3t t 3 0,
t (3 t 2 ) 0,
t1 0; t2; 3 3.
с Oy: x = 0
3t 2 0,
t 0.
-2
12
2
A2
-3
27
18
A1
3
3
9
0
A7
9
0
A3
27.
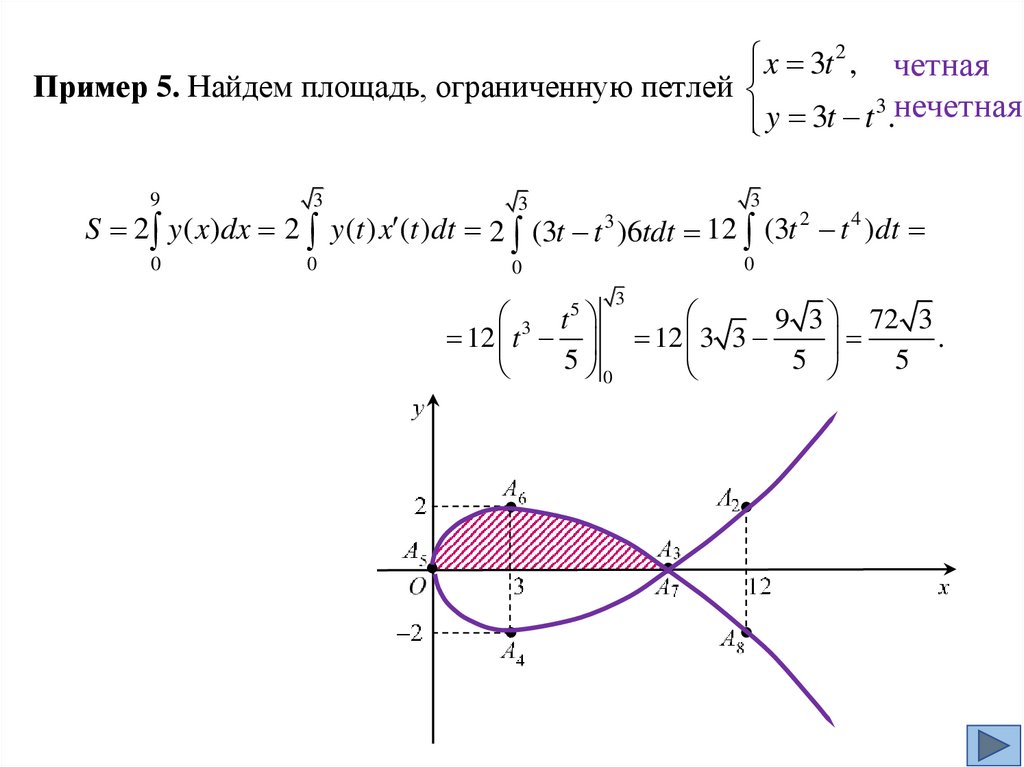
x 3t 2 , четнаяПример 5. Найдем площадь, ограниченную петлей
3
y 3t t .нечетная
9
3
3
3
0
0
0
0
S 2 y ( x)dx 2 y (t ) x (t )dt 2 (3t t 3 )6tdt 12 (3t 2 t 4 ) dt
3
3 t
9 3 72 3
12 t 12 3 3
.
5
5
5
0
5
28.
Пусть на плоскости задана полярная система координат.Совместим её с декартовой системой координат Oxy обычным
образом, т. е. так, чтобы полярная ось совпала с положительной
полуосью оси Ox, а направление отсчёта угла совпало с
направлением кратчайшего поворота от Ox к Oy.
Часть плоскости, ограниченную лучами φ = α, φ = β, где α ≤ β, и
кривой ρ = ρ(φ) (r = r(φ)), где функция ρ(φ) определена,
непрерывна и неотрицательна на [α,β], будем называть
криволинейным сектором.
28
29.
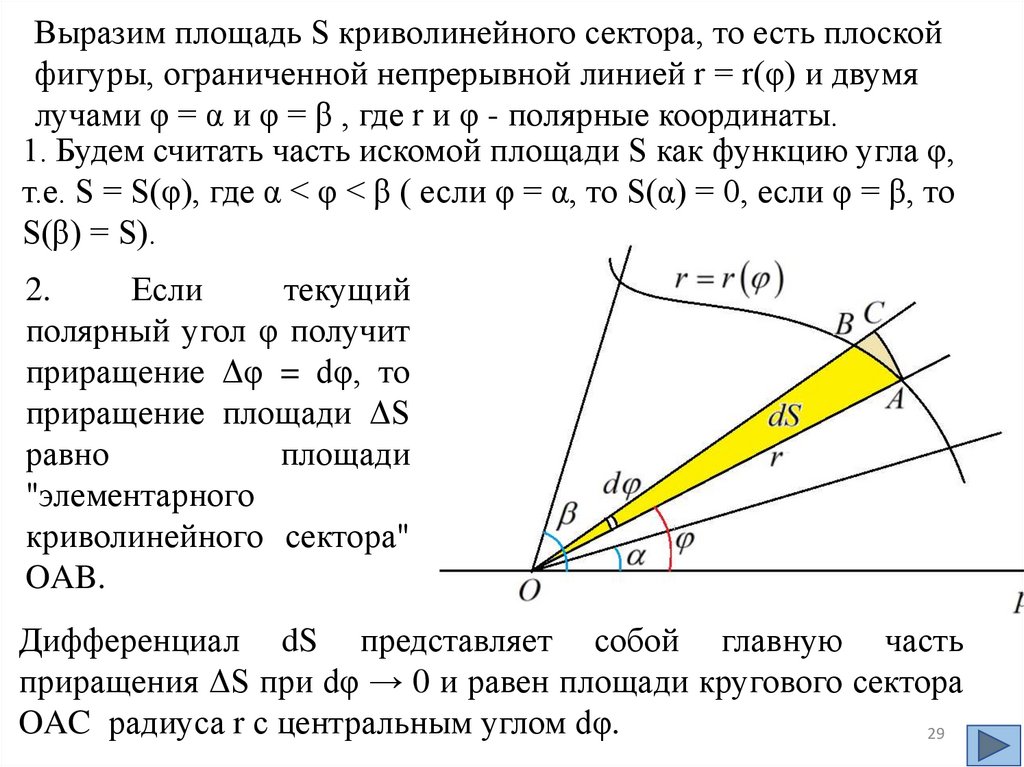
Выразим площадь S криволинейного сектора, то есть плоскойфигуры, ограниченной непрерывной линией r = r(φ) и двумя
лучами φ = α и φ = β , где r и φ - полярные координаты.
1. Будем считать часть искомой площади S как функцию угла φ,
т.е. S = S(φ), где α < φ < β ( если φ = α, то S(α) = 0, если φ = β, то
S(β) = S).
2.
Если
текущий
полярный угол φ получит
приращение Δφ = dφ, то
приращение площади ΔS
равно
площади
"элементарного
криволинейного сектора"
OAB.
Дифференциал dS представляет собой главную часть
приращения ΔS при dφ → 0 и равен площади кругового сектора
OAC радиуса r с центральным углом dφ.
29
30.
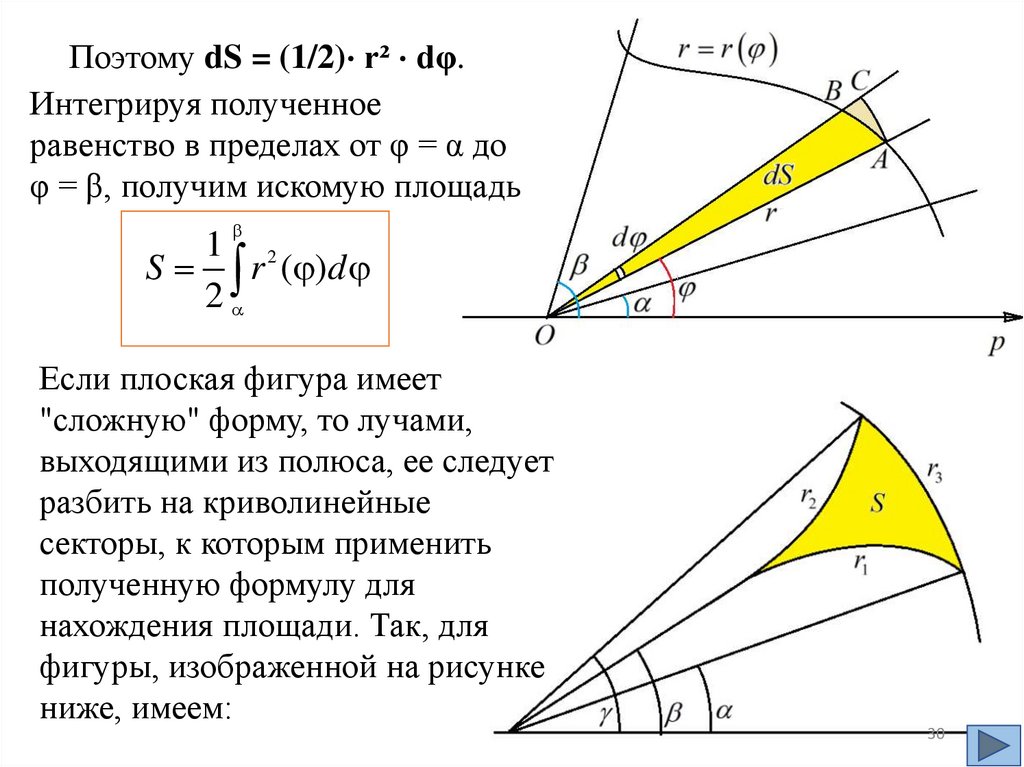
Поэтому dS = (1/2)⋅ r² ⋅ dφ.Интегрируя полученное
равенство в пределах от φ = α до
φ = β, получим искомую площадь
1 2
S r ( )d
2
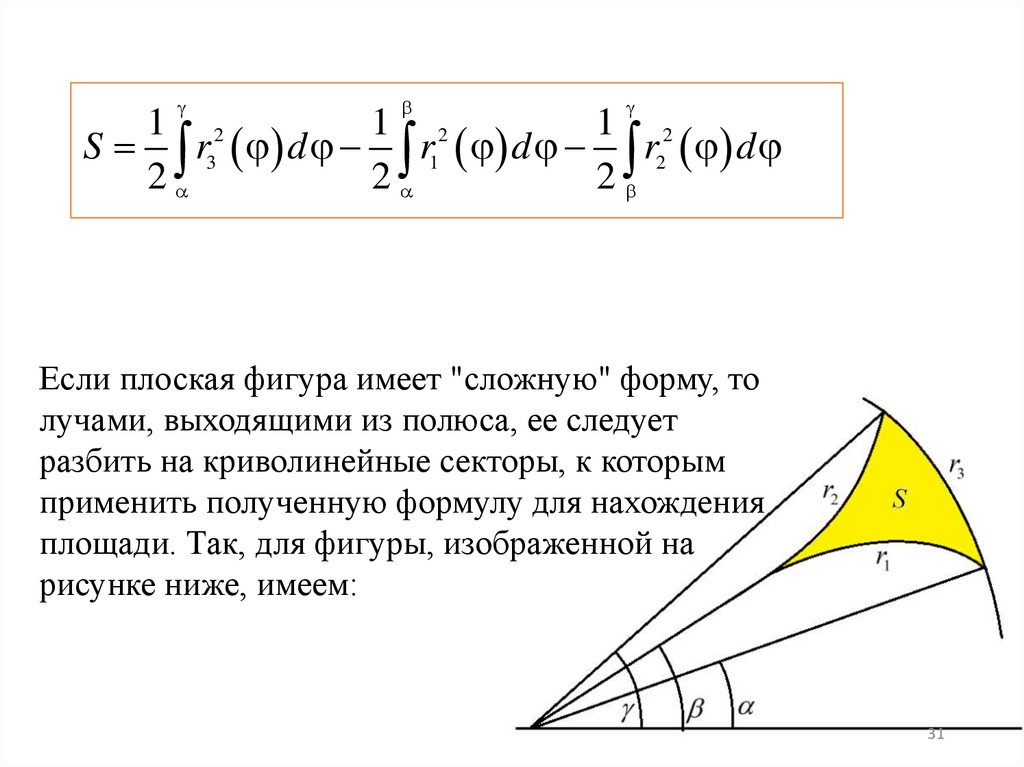
Если плоская фигура имеет
"сложную" форму, то лучами,
выходящими из полюса, ее следует
разбить на криволинейные
секторы, к которым применить
полученную формулу для
нахождения площади. Так, для
фигуры, изображенной на рисунке
ниже, имеем:
30
31.
1 21 2
1 2
S r3 d r1 d r2 d
2
2
2
Если плоская фигура имеет "сложную" форму, то
лучами, выходящими из полюса, ее следует
разбить на криволинейные секторы, к которым
применить полученную формулу для нахождения
площади. Так, для фигуры, изображенной на
рисунке ниже, имеем:
31
32.
Пример . Найти площадь фигуры, ограниченной кардиоидой –кривой
r 2 cos
Решение.
Кривая задана в полярных
координатах.
Так
как
уравнение не меняется при
замене φ на – φ, то кривая
симметрична относительно
полярной
оси
и
φ
изменяется от 0 до 2π.
32
33.
Так как фигура симметрична относительно полярной оси,то
1
S 2 (2 cos ) 2 d 4 4cos cos 2 d
20
0
1 cos 2
d
2
0
4d 4 cos d cos d 4 0 4sin 0
0
0
0
2
sin 2
9
4
20
4 0 2
33
34.
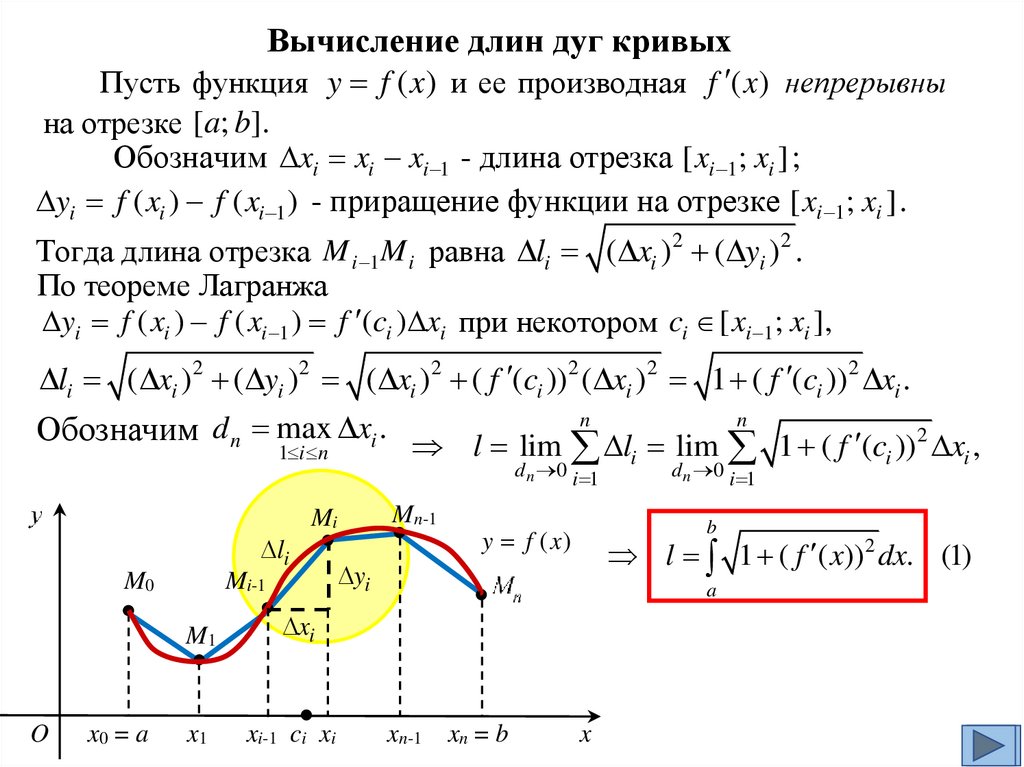
Вычисление длин дуг кривыхПусть функция y f ( x) и ее производная f ( x ) непрерывны
на отрезке [a; b].
y f ( x)
O
a
b
x
35.
Вычисление длин дуг кривыхПусть функция y f ( x) и ее производная f ( x ) непрерывны
на отрезке [a; b].
Разобьем отрезок [a; b] на n частичных отрезков точками
x0 , x1 , x2 , ..., xn , где x0 a x1 x2 ... xn b. Этим точкам
соответствуют точки M 0 , M 1 , M 2 , ..., M n на кривой.
M0
Mi
Mn-1
xi
xn-1 xn = b
y f ( x)
Mi-1
M1
O
x0 = a
x1
xi-1
x
36.
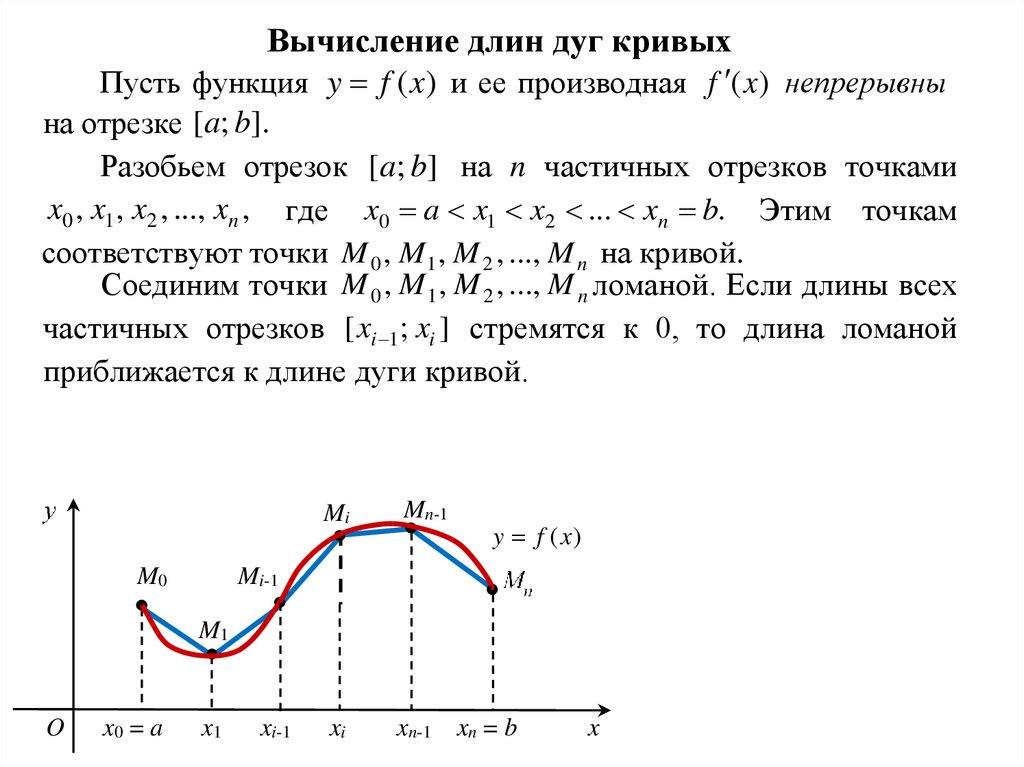
Вычисление длин дуг кривыхПусть функция y f ( x) и ее производная f ( x ) непрерывны
на отрезке [a; b].
Разобьем отрезок [a; b] на n частичных отрезков точками
x0 , x1 , x2 , ..., xn , где x0 a x1 x2 ... xn b. Этим точкам
соответствуют точки M 0 , M 1 , M 2 , ..., M n на кривой.
Соединим точки M 0 , M 1 , M 2 , ..., M n ломаной. Если длины всех
частичных отрезков [ xi 1; xi ] стремятся к 0, то длина ломаной
приближается к длине дуги кривой.
M0
Mi
Mn-1
xi
xn-1
y f ( x)
Mi-1
M1
O
x0 = a
x1
xi-1
xn = b
x
37.
Вычисление длин дуг кривыхПусть функция y f ( x) и ее производная f ( x ) непрерывны
на отрезке [a; b].
Обозначим xi xi xi 1 - длина отрезка [ xi 1; xi ] ;
yi f ( xi ) f ( xi 1 ) - приращение функции на отрезке [ xi 1; xi ] .
Тогда длина отрезка M i 1M i равна li ( xi )2 ( yi )2 .
По теореме Лагранжа
yi f ( xi ) f ( xi 1 ) f (ci ) xi при некотором ci [ xi 1; xi ],
li ( xi )2 ( yi )2 ( xi )2 ( f (ci ))2 ( xi )2 1 ( f (ci ))2 xi .
Обозначим d n max xi . l lim n l lim n 1 ( f (c ))2 x ,
1 i n
i
i
i
d n 0 i 1
li
M0
O
x0 = a
Mn-1
Mi
Mi-1
M1
xi
x1
xi-1 ci xi
d n 0 i 1
b
y f ( x)
l 1 ( f ( x))2 dx. (1)
yi
a
xn-1
xn = b
x
38.
Кривая l называется спрямляемой, если существует предел длинломаных линий, вписанных в эту кривую, при безграничном
увеличении количества элементов разбиения T и стремлении
максимального элемента разбиения λ(T) к нулю: lim l (T )
( T ) 0
Длиной кривой называется предел длин вписанной ломаной.
Теорема (о длине кривой)
Пусть функция f (x) непрерывна вместе со своей
производной на промежутке [a,b]. Тогда кривая,
являющаяся графиком этой функции, спрямляема, и её
длина может быть найдена по формуле
b
l 1 ( f ( x))2 dx
a
38
39.
Пример 6. Вычислить длину дуги кривой y 2 (2 x )3 ,отсекаемой прямой x 0.
Заданная кривая – полукубическая парабола с D( y ) ( ; 2].
Выразим:
3
y (2 x) 2 - линия симметрична относительно Ох.
3
y (2 x ) 2 ,
Найдем длину l1 одной ветви
расположенной в
верхней полуплоскости, при этом по условию 0 x 2.
b
l1 1 ( f ( x))2 dx
3
3
y (2 x) 2 y
2
a
2 x
2
2
4 9 2 x
9
3
1
2 x dx 1 2 x dx
dx
4
4
2
0
0
0
2
2
2
3
2
3
3
22 22 8
1
1 22 9 x
1 2
2
22 9 xdx
4 22
.
3
20
18
27
27
2
0
44 22 16
Тогда длина всей кривой l
.
27
2
40.
x x (t ),Если кривая задана параметрически уравнениями
y y (t ),
причем функции x(t ), y(t ) и их производные непрерывны на
отрезке [t1 ; t2 ] и x (t ) 0 при t [t1; t2 ],
y (t )
f ( x)
x (t )
b
l 1 ( f ( x)) dx
2
a
( x (t )) 2 ( y (t )) 2
( y (t )) 2
1 ( f ( x)) 1
2
x (t )
( x (t ))
2
dx x (t )dt
t2
l ( x (t ))2 ( y (t )) 2 dt ,
t1
причем здесь всегда t1 t2 .
!
(2)
Упражнение 1. Получить формулу (2), сделав замену
переменной в (1) с учетом того, что в силу ограничений на функцию
x(t ) ее производная сохраняет знак на всем отрезке [t1; t2 ], так что
если x (t ) 0 на [t1; t2 ], то x (t ) x (t ) и x (t1 ) a; x (t2 ) b, а если
x (t ) 0 на [t1; t2 ], то x (t ) x (t ) и x (t1 ) b; x (t2 ) a.
41.
Если кривая AB задана в полярной системе координатуравнением r=r(φ), для φє[α,β]
Если в равенствах x r cos ,
y r sin ,
связывающих декартовые координаты,
параметром считать угол φ , то кривую
можно задать параметрически
x r cos ,
Последовательно найдём:
y r sin ,
x r cos r sin ,
y r sin r cos ,
2
2
2
2
2
x
r
cos
2
r
r
sin
cos
r
sin
,
2
2
2
2
2
y
r
sin
2
r
r
sin
cos
r
cos
,
41
42.
dl x y d2
2
r 2 cos 2 2rr sin cos r 2 sin 2 r 2 sin 2 2rr sin cos r 2 cos 2 d
r 2 cos2 r 2 sin 2 r 2 sin 2 r 2 cos2 d
r r d
2
2
то длина l дуги AB вычисляется по формуле
l r 2 r '2 d
2
2
2
2
2
x
r
cos
2
r
r
sin
cos
r
sin
,
2
2
2
2
2
y
r
sin
2
r
r
sin
cos
r
cos
,
42
43.
Пример. Найти длину кардиоиды r 1 cosРешение. С учетом симметрии графика
относительно полярной оси получаем
l r 2 r '2 d 2 (1 cos )2 sin d
2
0
2
0
2 2cos d 1 cos 2sin 2 2 4sin 2 d
2
2
0
4 sin d 4 2 sin d 8 cos 8
2
2 0
2 2
0
0
43
44.
Рассматривая длину кривой на отрезке [a; x ] с переменным правымконцом, по формуле (1) получим функцию зависимости длины кривой от x:
x
l ( x ) 1 ( f ( x ))2 dx,
a
откуда по теореме о производной определенного интеграла по переменному
верхнему пределу получим выражение дифференциала длины дуги в виде
dl l ( x)dx 1 ( f ( x))2 dx.
Аналогично из (2) получаем выражение дифференциала длины дуги
кривой, заданной параметрически:
dl ( x (t ))2 ( y (t ))2 dt.
Эти формулы используются
интегралов 1-го рода.
при
вычислении
криволинейных
45.
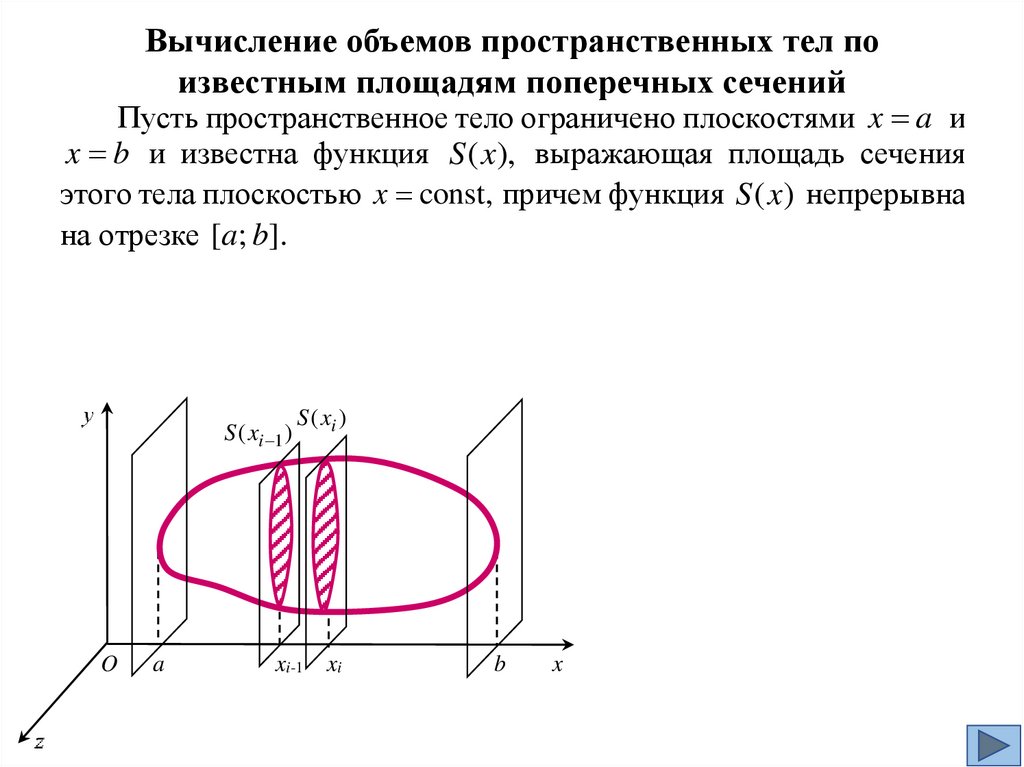
Вычисление объемов пространственных тел поизвестным площадям поперечных сечений
Пусть пространственное тело ограничено плоскостями x a и
x b и известна функция S ( x), выражающая площадь сечения
этого тела плоскостью x const, причем функция S ( x) непрерывна
на отрезке [a; b].
S ( xi 1 )
O
a
S ( xi )
xi-1
xi
b
x
46.
Вычисление объемов пространственных тел поизвестным площадям поперечных сечений
Разобьем отрезок [a; b] на n частичных отрезков точками
x0 , x1 , x2 , ..., xn , где x0 a x1 x2 ... xn b.
Если длины всех частичных отрезков достаточно малы, то
каждый слой тела, отвечающий отрезку [ xi 1 ; xi ], можно
рассматривать приблизительно как цилиндр с основанием S ( ci )
при некотором ci [ xi 1 ; xi ] и высотой xi xi xi 1 .
d n max xi 0,
S ( xi 1 )
1 i n
S ( xi )
n
V lim S (ci ) xi ,
d n 0 i 1
b
V S x dx.
a
O
a
xi-1
xi
b
x
(3)
47.
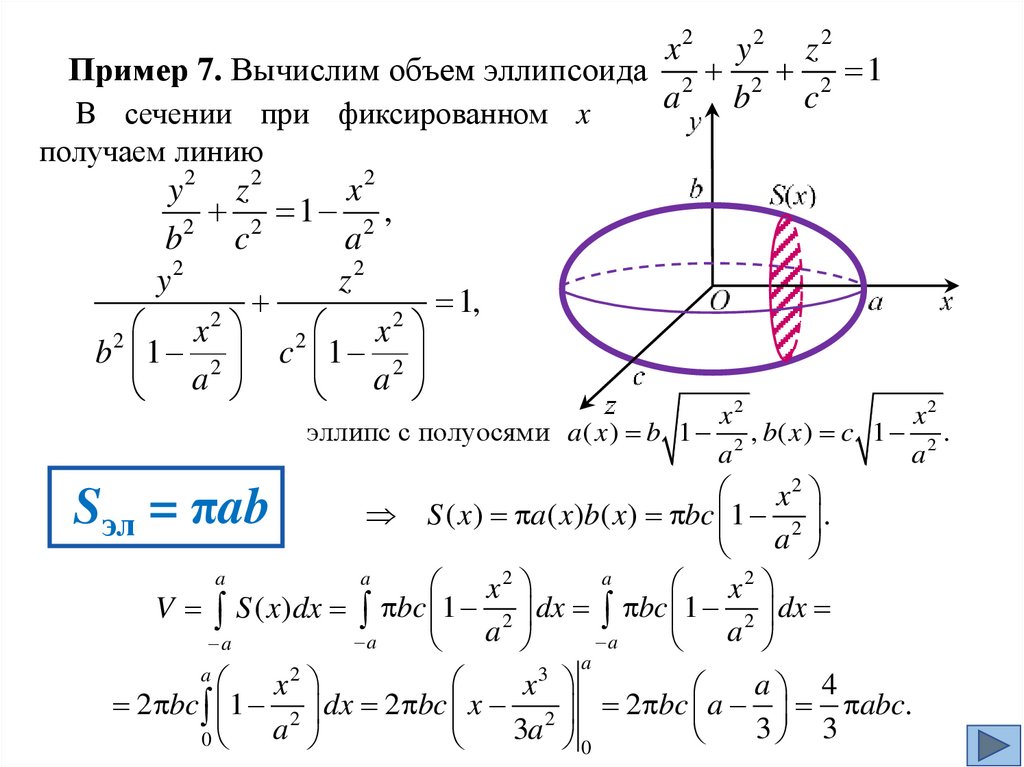
x2 y 2 z 2Пример 7. Вычислим объем эллипсоида 2 2 2 1
a
b
c
В сечении при фиксированном x
получаем линию
y2 z2
x2
2 1 2 ,
2
b
c
a
y2
z2
1,
2
2
x
x
2
2
b 1 2 c 1 2
a
a
x2
x2
эллипс с полуосями a ( x ) b 1 2 , b( x ) c 1 2 .
a
a
x2
S ( x) a( x)b( x) bc 1 2 .
эл
a
a
a
a
x2
x2
V S ( x)dx bc 1 2 dx bc 1 2 dx
a
a
a
a
a
a
2
3
a
x
x
a 4
2 bc 1 2 dx 2 bc x 2 2 bc a abc.
3 3
a
3a
0
S = πab
0
48.
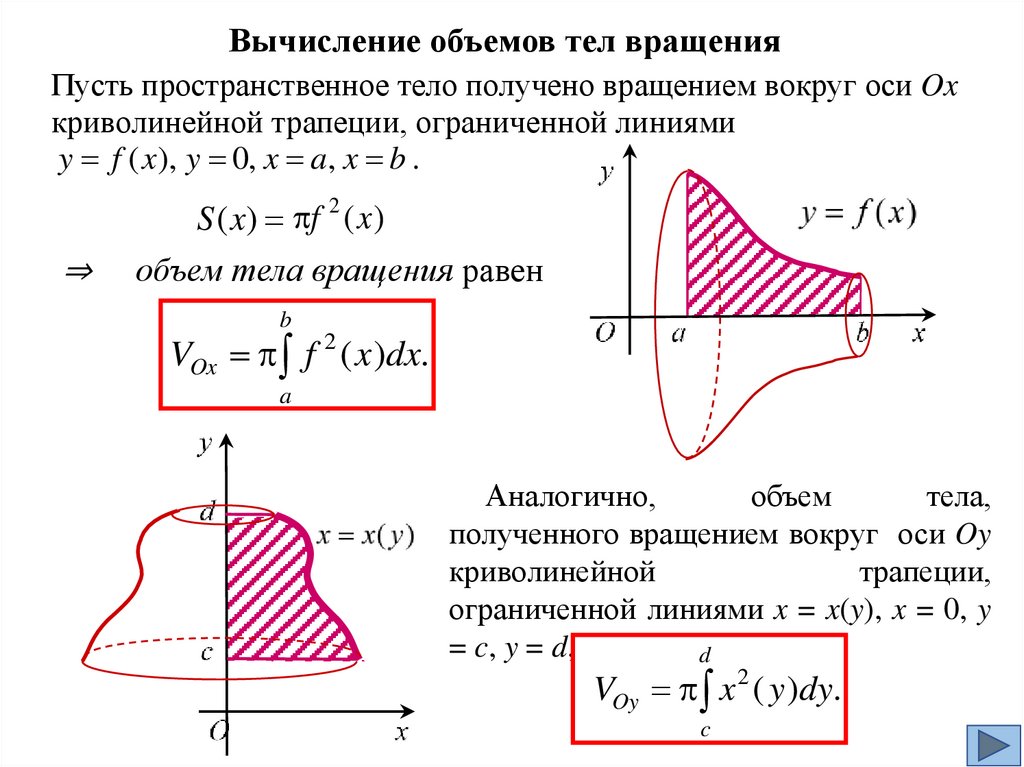
Вычисление объемов тел вращенияПусть пространственное тело получено вращением вокруг оси Ox
криволинейной трапеции, ограниченной линиями
y f ( x), y 0, x a, x b .
⇒
S ( x) f 2 ( x )
объем тела вращения равен
b
VOx f 2 ( x )dx.
a
Аналогично,
объем
тела,
полученного вращением вокруг оси Oy
криволинейной
трапеции,
ограниченной линиями x = x(y), x = 0, y
= c, y = d,
d
VOy x 2 ( y )dy.
c
49.
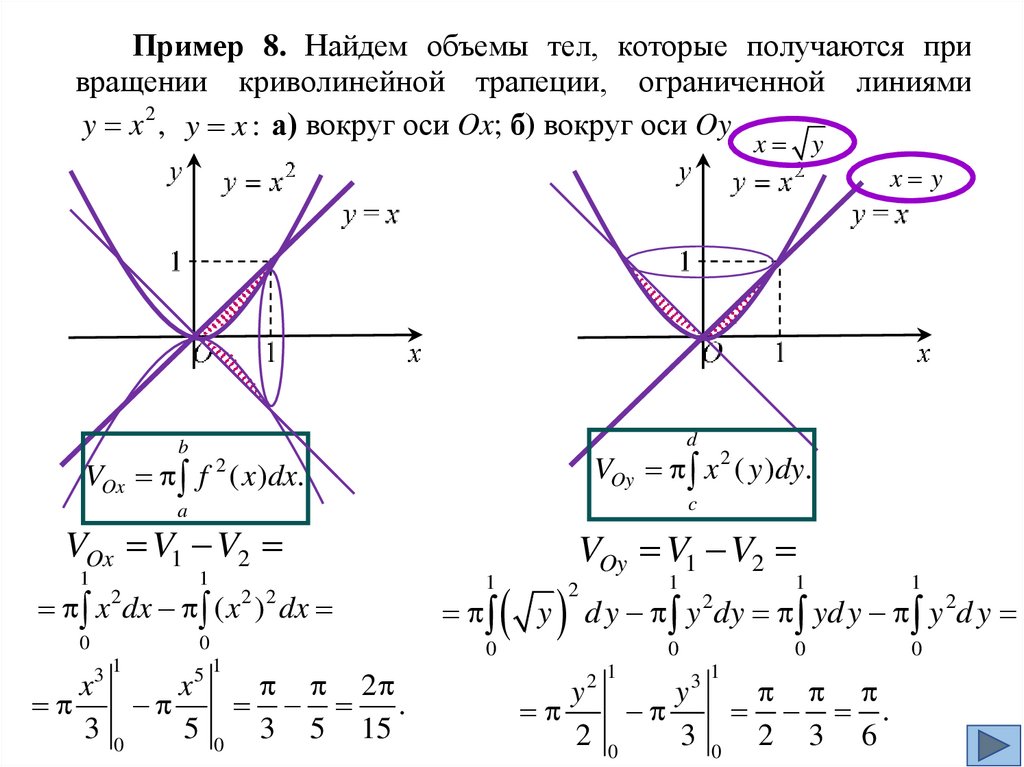
Пример 8. Найдем объемы тел, которые получаются привращении криволинейной трапеции, ограниченной линиями
y x 2 , y x : а) вокруг оси Ox; б) вокруг оси Oy.
x y
x y
d
b
VOy x 2 ( y )dy.
VOx f ( x )dx.
2
c
a
VOx V1 V2
1
1
x dx ( x ) dx
2
0
2 2
0
31
5 1
x
x
2
.
3 0
5 0 3 5 15
1
y
VOy V1 V2
2
1
1
0
0
d y y dy yd y y 2d y
0
0
1
2
2 1
3 1
y
y
.
2 0
3 0 2 3 6
50.
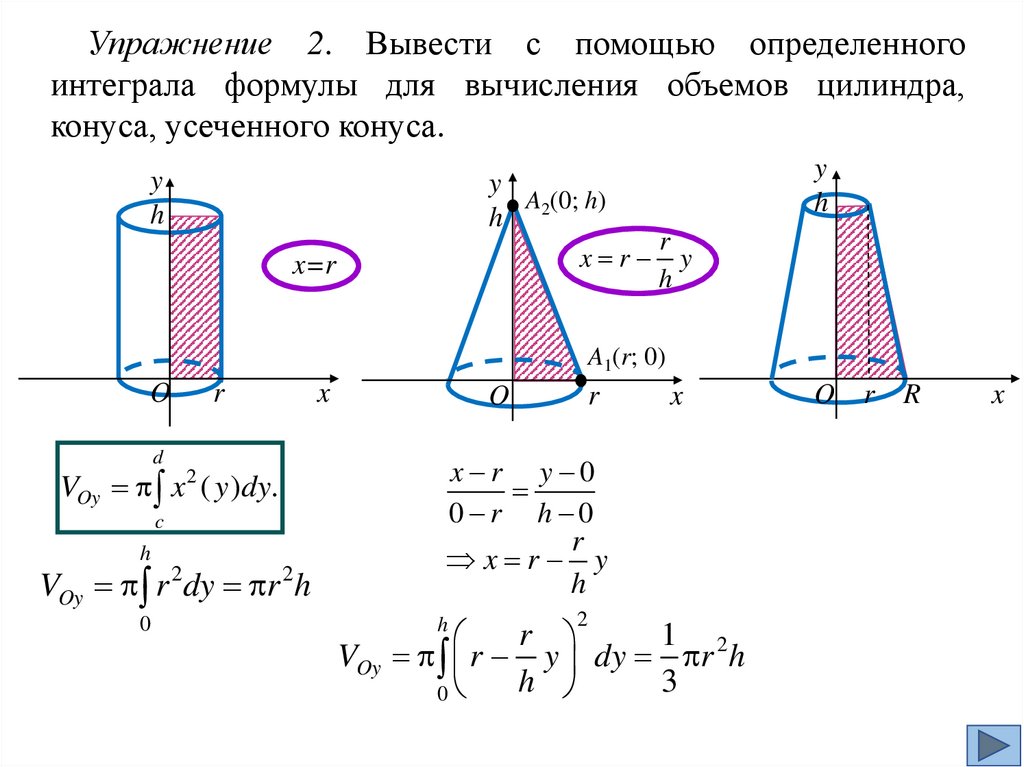
Упражнение 2. Вывести с помощью определенногоинтеграла формулы для вычисления объемов цилиндра,
конуса, усеченного конуса.
y
h
y
A (0; h)
h 2
r
x r y
h
x=r
y
h
A1(r; 0)
O
r
d
VOy x 2 ( y )dy.
c
h
VOy r 2dy r 2h
0
x
O
r
x
x r y 0
0 r h 0
r
x r y
h
2
r
1
VOy r y dy r 2h
h
3
0
h
O r R
x
51.
Вычисление площадей поверхностей тел вращенияПусть функция y f ( x) и ее производная f ( x ) непрерывны
на отрезке [a; b]. Площадь поверхности, образованной вращением
линии y f ( x ), a x b, вокруг оси Ox, равна
b
SOx 2 f ( x ) 1 ( f ( x ))2 dx.
a
Аналогично, если функция x x( y ) и ее производная x ( y )
непрерывны на отрезке [c; d ], то площадь поверхности,
образованной вращением линии x x( y ), c y d , вокруг оси Oy,
равна
d
SOy 2 x( y ) 1 ( x ( y ))2 dy.
c
Упражнение 3. Вывести с помощью определенного
интеграла формулы для вычисления площадей боковых
поверхностей цилиндра, конуса, усеченного конуса.
52.
x x (t ),Если кривая задана параметрически уравнениями
y y (t ),
t1 t t2 , то площадь поверхности вращения вычисляется по
формуле
t2
Sох 2 y (t ) ( xt ) 2 ( yt ) 2 dt
t1
Пример . Вычислить площадь S поверхности, полученной
вращением одной арки циклоиды x a (t sin t )
0 t 2
вокруг оси OX
y a (1 cos t )
Решение. 2
S 2 a(1 cos t ) (a sin t )2 (a(1 cos t )) 2 dt
2
0
2
3
2
2
2
3 t
2 t
2 2 a (1 cos t ) dt 2 2 a 2sin dt 8 a sin dt
2
2
2 0
0
0
3 t
2
cos
t
t
t
2
16 a 2 1 cos 2 d cos 16 a 2 cos
2
2
2
3
64 a 2 0
(кв. ед.)
52
0
3
2
3
2
2
53.
Физические приложения определенного интеграла1. Нахождение пути, пройденного телом при прямолинейном
t2
t2
движении.
S v t dt
V a t dt
t1
t1
где V–скорость прямолинейного движения, а –ускорение.
Пример
Два тела начали двигаться одновременно из одной точки в
одном направлении по прямой. Первое тело движется со
скоростью v1 = 6t2 + 2t (м/с), второе — со скоростью v2 = 4t + 5
(м/с). На каком расстоянии S друг от друга они окажутся через
5 с? Решение
5
S1 6t 2t dt 2t t 0 275( м)
2
0
3
5
2
5
S2 4t 5 dt 2t 5t 75 м
2
5
0
0
Таким образом, S=275-75=200 м
53
54.
2. Вычисление работы. Работу А, произведенную переменнойсилой f(x) при перемещении по оси Ох материальной точки от
b
х = а до х = b, находим по формуле
A F ( x)dx
a
При решении задач на вычисление работы силы, связанных с
растяжением-сжатием
пружин,
основываются
на
соотношении закона Гука F=k x, где F — сила; х —
абсолютное удлинение пружины, вызванное силой F; к —
коэффициент пропорциональности.
Пример
Укорочение х винтовой пружины при сжатии
пропорционально приложенной силе F. Вычислить
работу А силы F при сжатии пружины на 0,04 м,
если для сжатия ее на 0,01 м нужна сила 10 Н.
Решение
F =k x , по условию 10=0,01k, следовательно, k
=1000 Н/м, поэтому в данной задаче F = 1000х.
0,04
A 1000 x dx 500 x 2
0,04
0
0,8( Дж)
54
55.
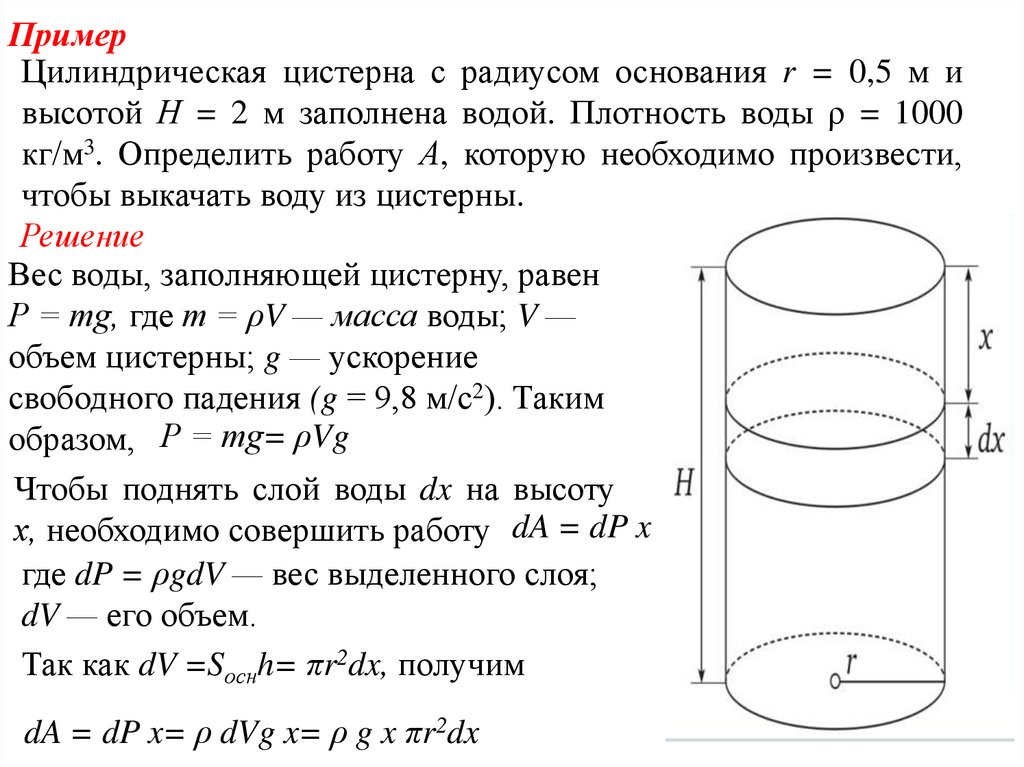
ПримерЦилиндрическая цистерна с радиусом основания r = 0,5 м и
высотой Н = 2 м заполнена водой. Плотность воды ρ = 1000
кг/м3. Определить работу А, которую необходимо произвести,
чтобы выкачать воду из цистерны.
Решение
Вес воды, заполняющей цистерну, равен
Р = mg, где т = ρV — масса воды; V —
объем цистерны; g — ускорение
свободного падения (g = 9,8 м/с2). Таким
образом, Р = mg= ρVg
Чтобы поднять слой воды dx на высоту
х, необходимо совершить работу dA = dP x
где dP = ρgdV — вес выделенного слоя;
dV — его объем.
Так как dV =Sоснh= πr2dx, получим
dA = dP x= ρ dVg x= ρ g x πr2dx
55
56.
Для того чтобы получить выражение для работы А, следует взятьопределенный интеграл в пределах от 0 до Н:
H
H
2 H
H
x
A dA g r xdx g r x dx g r
2 0
0
0
0
2
2
2
2
2
H
2
g r 2
10009,8 0,52 15400( Дж)
2
2
dA = dP x= ρ dVg x= ρ g x πr2dx
56
57.
ПримерВычислить работу, необходимую для выкачивания воды из
котла, имеющего форму полушара радиуса R.
Решение
Так как сила, которую надо
прикладывать к каждой частице
при ее поднятии, равна весу
частицы, то работа по поднятию
одной
частицы
равна
произведению массы частицы на
глубину ее погружения.
Рассмотрим слой воды шириной dx,
находящийся на глубине х от поверхности
воды. Элементарная работа по поднятию этого слоя выразится
dA = γ x π y2dx
где γ =1– плотность воды: y2 = R2 – x2 ; πy2 dx – объем
элементарного слоя: γ π y2dx ⋅ – масса слоя.
57
58.
dA = γ x π (R2 – x2 ) dxТак как х меняется от 0 до R, то вся работа
R
x
2x
A dA R x xdx R x x dx R
2 4 0
0
0
0
R
R
R
2
2
2
2
4
3
R 4 R 4 R 4
4
4
2
58
59.
ПримерС какой силой вода давит на вертикальный прямоугольный шлюз
с основанием 18 м и высотой 6 м?
Решение
Сила, с которой вода давит на
каждую точку, находящуюся на
высоте х от поверхности воды
прямоугольного вертикального
шлюза, равна весу столба воды,
находящегося над этим уровнем.
Выделим элементарную площадь шириной dх у шлюза на высоте
х от поверхности.
Величина давления жидкости на горизонтальную площадку
зависит от глубины ее погружения х, т.е. от расстояния
площадки до поверхности жидкости : P = δ ⋅ S x , где δ –
удельный вес жидкости; S – площадь заштрихованной полоски.
Сила давления воды будет некоторой функцией P(х). Найдем
59
дифференциал dP этой функции.
60.
Допустим ввиду малости dх, что все точки заштрихованнойполоски находятся на глубине х.
Тогда приближенная величина
давления воды на эту полоску
будет равна весу столба воды,
имеющего основанием эту
полоску, а высоту, равную
глубине х.
Следовательно, dp =18δ ⋅ xdx =18xdx (удельный вес воды δ=1г/ см3 )
Величина давления жидкости на горизонтальную площадку
зависит от глубины ее погружения х, т.е. от расстояния
площадки до поверхности жидкости : P = δ ⋅ S x , где δ –
удельный вес жидкости; S – площадь заштрихованной полоски.
Сила давления воды будет некоторой функцией P(х). Найдем
60
дифференциал dP этой функции.
61.
Допустим ввиду малости dх, что все точки заштрихованнойполоски находятся на глубине х.
Тогда приближенная величина
давления воды на эту полоску
будет равна весу столба воды,
имеющего основанием эту
полоску, а высоту, равную
глубине х.
Следовательно, dp =18δ ⋅ xdx =18xdx (удельный вес воды δ=1г/ см3 )
Согласно условию задачи глубина х изменяется на отрезке [0;6],
поэтому искомое давление на весь шлюз найдем, интегрируя dp в
пределах от 0 до 6, т.е.
6
6
6
P dp 18 xdx 18x dx 9 x 0 108(т) 108000 9,81( Н )
2 6
0
0
0
1059480( Н )
( Н (ньютон) – единица силы (веса), 1Н ≈ 0,102кг ; 1кг ≈ 9,81Н61)
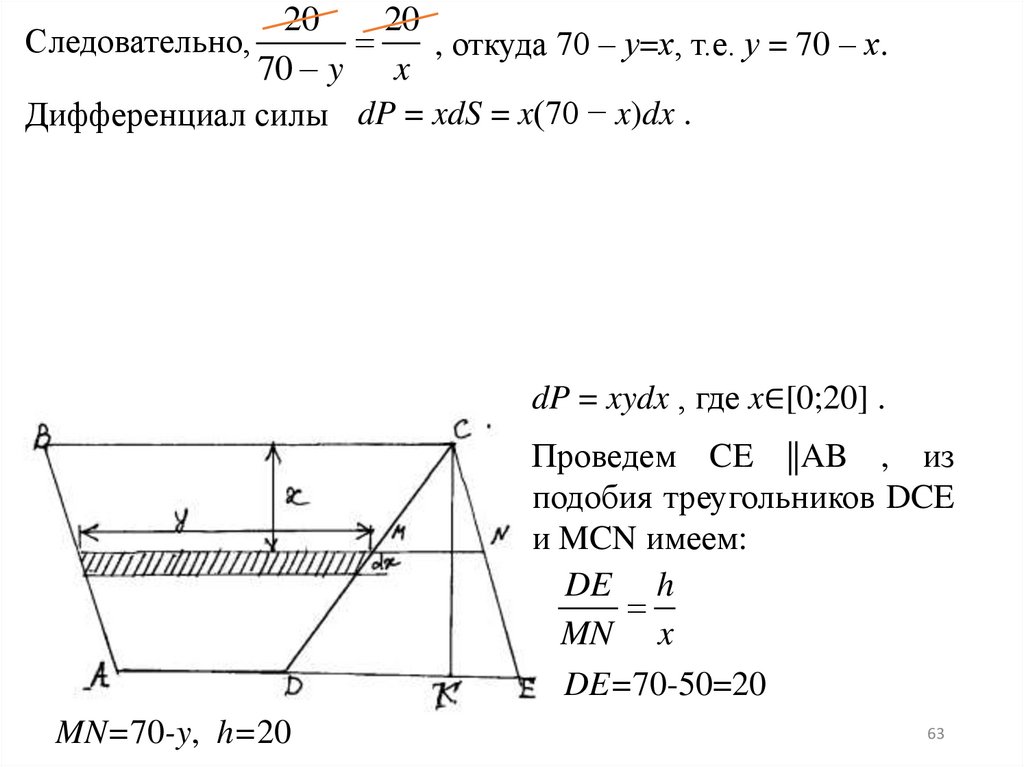
62.
ПримерВычислить, с какой силой вода давит на вертикальную плотину,
имеющую форму трапеции, верхнее основание которой равно 70
м, нижнее 50 м, а высота 20 м .
Решение
Допуская, что заштрихованная полоска шириной dх расположена
на глубине х в горизонтальной плоскости и что она является
прямоугольником со сторонами dх и у, найдем приближенно силу
давления воды на эту полоску.
dP = xydx , где x∈[0;20] .
Проведем CE ||AB , из
подобия треугольников DCE
и MCN имеем:
DE h
MN x
DE=70-50=20
MN=70-y, h=20
62
63.
2020
Следовательно,
, откуда 70 – у=х, т.е. у = 70 – х.
70 y x
Дифференциал силы dP = xdS = x(70 − x)dx .
dP = xydx , где x∈[0;20] .
Проведем CE ||AB , из
подобия треугольников DCE
и MCN имеем:
DE h
MN x
DE=70-50=20
MN=70-y, h=20
63
64.
2020
Следовательно,
, откуда 70 – у=х, т.е. у = 70 – х.
70 y x
Дифференциал силы dP = xdS = x(70 − x)dx .
20
x
2
P dp x 70 x dx 70 x x dx 35 x
3 0
0
0
0
20
20
20
3
2
14000
8000 50000
т ...
3
3
64
65.
ПримерВычислить работу, которую необходимо затратить, чтобы
поднять тело массы m с поверхности Земли на высоту h (радиус
Земли R=6400км). С помощью полученного результата
определить вторую космическую скорость (скорость, при
которой вертикально поднимающееся тело может подняться на
любую высоту).
Решение На ракету, имеющую массу m, по закону всемирного
mM
тяготения действует сила
F G
x2
где G – гравитационная постоянная; M – масса
Земли; m – масса ракеты, x∈[R, R + h]
Полагая, что работа, совершаемая двигателем
ракеты при подъеме ее на высоту x, есть некоторая
функция A(x), и допуская, что при дальнейшем
подъеме на бесконечно малую высоту dx сила F
остается неизменной, найдем приближенную
величину приращения работы
65
66.
mMA F x dx G 2 dx dA
x
Работа
R h
R h
R h
mM
dx
A dA F x dx G 2 dx GmM 2
x
R
R x
R
R
R h
R h
GmM h
1
1
1
GmM GmM
x R
R R h R R h
В то же время работа равна изменению кинетической энергии
2
ракеты A = ∆W =|W₂ −W₁| = mv
2
Чтобы рассчитать вторую космическую скорость, которую надо
сообщить ракете у поверхности Земли для преодоления земного
притяжения, нужно положить h = +∞ .
GmM h
GmM
Тогда A lim
h
R R h
R
2
GmM
mv
следовательно,
R
2
66
67.
2GMv
R
2
Так как GM g 9,8 м / с 2
2
R
v 2 gR 2 9,8 6,4 106 м / с 11,2 103 м / с
Чтобы рассчитать вторую космическую скорость, которую надо
сообщить ракете у поверхности Земли для преодоления земного
притяжения, нужно положить h = +∞ .
GmM h
GmM
Тогда A lim
h
R R h
R
2
GmM
mv
следовательно,
R
2
67
68.
2GMv
R
2
Так как GM g 9,8 м / с 2
2
R
v 2 gR 2 9,8 6,4 106 м / с 11,2 103 м / с
Вторая космическая скорость v 11,2 103 м / с
68
69.
ПримерВычислить работу, которую надо затратить, чтобы выкачать воду
из резервуара, имеющего форму усеченного конуса высотой h,
если радиус нижнего основания r, а верхнего R, R>r
Решение
Будем
считать,
что
элементарный
слой
воды,
находящийся на глубине x ,
имеет форму прямого кругового
цилиндра
высотой
dx
с
радиусом основания p = r + y .
Из подобия ∆ABC и ∆DBE имеем
R r h x
y
R r
y
h
h x
h
Следовательно,
R r h x R R r x
r
p=r+y=
h
h
Тогда объем элементарного слоя будет равен
2
2
R r
R r
R r 2
x
dV R
x dx R 2 R
x dx
h
h
h
2
2
69
70.
Элементарная работа, совершаемая для поднятия этого слоя на2
высоту x , равна
R r
dA gx R
x dx
h
где ρ=1 – плотность воды; g – гравитационная постоянная.
Следовательно,
Тогда объем элементарного слоя будет равен
2
R r
R r 2
2
R r
x
x dx
dV R
x dx R 2 R
h
h
h
2
70
71.
Элементарная работа, совершаемая для поднятия этого слоя на2
высоту x , равна
R r
dA gx R
x dx
h
где ρ=1 – плотность воды; g – гравитационная постоянная.
2
h
h
Следовательно,
R r
A dA gx R
x dx
h
0
0
2
h
2
R r 2 R r 3
g xR 2 R
x
x dx
h
h h
0
2
3
2 x2
R r x R r x4
g R
2R
2
h 3 h 4
0
2
2
3
4
2h
R r h R r h
g R
2R
2
h 3 h 4
2
7
1 2
2 17
2
2
1
2
2 R
g h R R r R r g h R Rr r
3
4
12
4
2 3
71
72.
ПримерНайти силу давления воды на вертикальную треугольную пластинку
с основанием a и высотой h, погруженную в жидкость
Решение
Рассмотрим горизонтальную полоску, находящуюся на глубине x
и имеющую ширину dx . Приближенно можно считать эту
полоску прямоугольником, площадь которого dS = MN ⋅dx .
Из подобия треугольников ABC и MBN
x
имеем x MN
MN
a
h
h
a
ax
dS = MN ⋅dx= dx
h
Сила давления воды на эту полоску
приближенно
равна
2
ax
ax
dx x∈[0,h]
dP x dS x dx
h
h
Тогда сила давления на всю пластинку ABC равна
h
h
ax 2
ax 3
P
dx
h
3h
ah 3 ah 2
3h
3
72
73.
Моменты и центры масс плоских кривыхCтатический момент материальной точки массы m
относительно некоторой оси равен произведению массы m на
расстояние d точки до оси. Для системы n материальных точек
с массами m1, m2,…mn, лежащих в одной плоскости с осью,
соответственно на расстояниях d1, d2,…dn от оси L, статический
n
момент выразится суммой M m d
L
i
i
i 1
При этом расстояния точек, лежащих по одну сторону от оси,
берутся со знаком плюс, а по другую сторону – со знаком
минус.
Если же массы не сосредоточены в отдельных точках, но
расположены сплошным образом, заполняя линию или
плоскую фигуру, то для выражения статического момента
вместо суммы потребуется интеграл.
73
74.
Если дуга материальной кривой задана уравнением y=f (x)a≤x≤b и имеет плотность ρ=ρ(x), то:
1) статические моменты этой дуги Mx и My
осей OX и OY соответственно равны
относительно
b
b
2
M
(
x
)
x
1
(
f
(
x
))
dx
M x ( x) f ( x) 1 ( f ( x)) dx
y
2
a
a
2) моменты инерции Ix и Iy относительно осей OX и OY
вычисляются по формулам
b
b
a
a
I x ( x) f 2 ( x) 1 ( f ( x))2 dx I y ( x) x 2 1 ( f ( x)) 2 dx
Статические моменты Мх и Му кривой позволяют установить
положение ее центра тяжести x, y , обладающего тем свойством,
что если в нем сосредоточить всю “массу” кривой АВ, то
статический момент этой массы относительно любой оси равен
моменту всей кривой относительно этой оси.
74
75.
3) координаты центра тяжести этой кривой вычисляются поMy 1 b
формулам
2
x
m
( x) x 1 ( f ( x)) dx
m
a
Mx 1 b
у
( x) f ( x) 1 ( f ( x)) 2 dx
m ma
b
где m ( x) 1 f ( x) dx - масса дуги.
2
a
В частности, если кривая однородная, т.е. ρ = const. для ординаты
центра тяжести получаем замечательное геометрическое
b
следствие.
2
у L f ( x) 1 ( f ( x)) dx
a
b
2 у L 2 f ( x) 1 ( f ( x))2 dx
a
75
76.
В правой части равенства имеем площадь Sox поверхности,полученной от вращения кривой АВ вокруг оси Oх, в левой
части c 2πӯ –длина окружности, описанной центром тяжести
при этом вращении.
Теорема Гульдена.
Площадь поверхности, полученной от вращения кривой около
некоторой не пересекающей ее оси, равна длине дуги этой
кривой, умноженной на длину окружности, описанной
центром тяжести кривой
b
у L f ( x) 1 ( f ( x))2 dx
a
b
2 у L 2 f ( x) 1 ( f ( x))2 dx
a
76
77.
Статические моменты и координаты центра тяжестиплоской фигуры
Если материальная плоская область ограничена кривой
y=f(x)≥0 , прямыми x=a, x=b ,y=0 и имеет постоянную плотность
ρ, то:
1) Статические моменты относительно осей Ox и Oy
b
соответственно равны
b
Mx
2
y
dx M y xy dx
2a
a
2) Координаты центра тяжести плоской области находятся по
формулам
b
b
b
b
x ab
a
xy dx xy dx
y dx
a
S
y
1 2
y dx
2a
b
y dx
1 2
y dx
2a
S
a
77
78.
Из формулы для ординаты центра тяжести получаем второеb
важное геометрическое следствие.
2
b
2 S y y 2 dx
2S y y dx
a
a
Правая часть равенства выражает объем V тела, полученного от
вращения плоской фигуры ограничена кривой y=f(x)≥0 ,
прямыми x=a, x=b ,y=0 вокруг оси Ох, левая часть выражает
произведение площади этой фигуры S на c 2πӯ длину
окружности, описанной центром тяжести фигуры
2) Координаты центра тяжести плоской области находятся по
формулам
b
b
b
b
x ab
a
xy dx xy dx
y dx
a
S
y
1 2
y dx
2a
b
y dx
1 2
y dx
2a
S
a
78
79.
Из формулы для ординаты центра тяжести получаем второеb
важное геометрическое следствие.
2
b
2 S y y 2 dx
2S y y dx
a
a
Правая часть равенства выражает объем V тела, полученного от
вращения плоской фигуры ограничена кривой y=f(x)≥0 ,
прямыми x=a, x=b ,y=0 вокруг оси Ох, левая часть выражает
произведение площади этой фигуры S на c 2πӯ длину
окружности, описанной центром тяжести фигуры.
Вторая теорема Гульдина: объем тела вращения плоской
фигуры около не пересекающей ее оси равен произведению
площади этой фигуры на длину окружности, описанной
центром тяжести фигуры.
V= 2πӯS
79
80.
Пример. Найти объем тела, полученного при вращениипрямоугольника вокруг оси, проходящей через его вершину
перпендикулярно диагонали, если длина прямоугольника равна
8, а ширина 6.
Решение. Центр тяжести прямоугольника лежит
на пересечении диагоналей, то его расстояние до оси равно
половине диагонали
d a 2 b2
82 62 10
Половина диагонали равна 5.
Тогда объем тела, пользуясь теоремой Гульдина V= 2πӯS
V = 2π ⋅5⋅6⋅8 = 480π .
80






























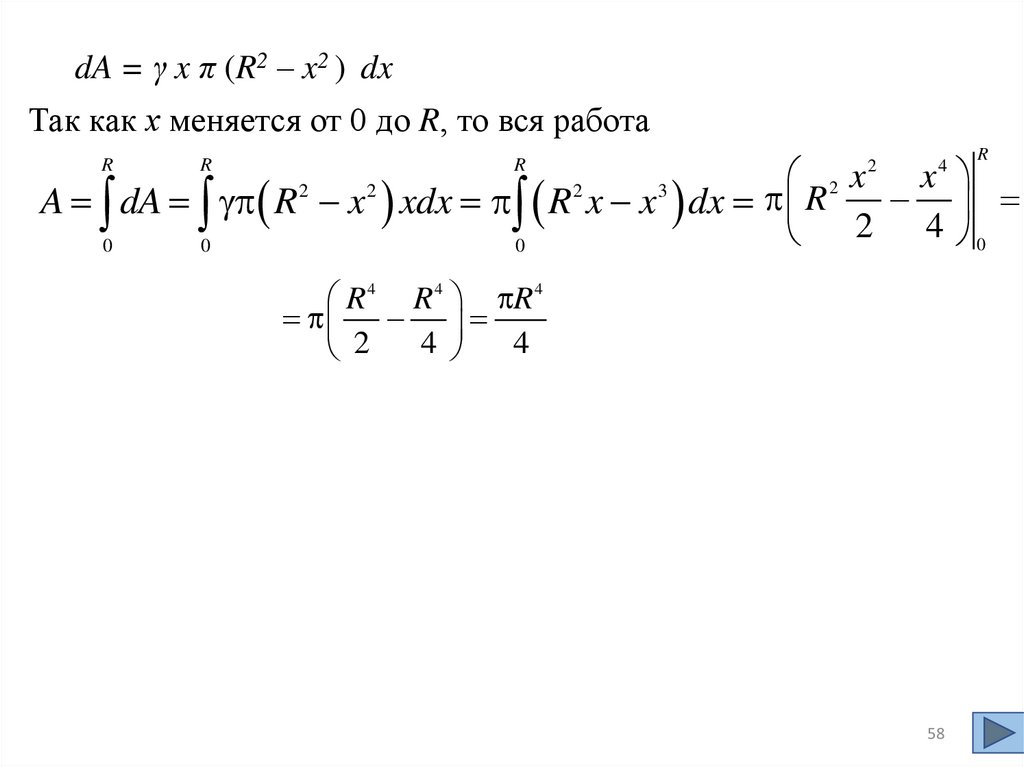





















 mathematics
mathematics








