Лекция5_Разложение_на_простые_множители

1. Лекция 5

Методы разложения целых
чисел на простые множители
Китайская теорема об остатках
1

2. Введение

Разложение на множители — предмет
непрерывного исследования в прошлом;
такие же исследования, вероятно,
продолжатся и в будущем.
Разложение на множители играет очень важную
роль в безопасности некоторых криптосистем с
открытым ключом
2

3. Основная теорема арифметики

Любое положительное целое число n, большее единицы,
может быть уникально записано в виде разложения на
простые множители:
n p p ... p
e1
1
e2
2
ek
k
где p1, p2, ..., pk — попарно различные простые числа и
e1, e2, ..., ek — положительные целые числа.
3

4. Приложения разложения на множители

1. Наибольший общий делитель двух чисел a и b может
быть найден, если мы знаем разложение на множители
чисел a и b:
a p1a1 p2a2 ... pkak ; b p1b1 p2b2 ... pkbk
НОД (a, b) p1min( a1 ,b1 ) p2min( a2 ,b2 ) ... pkmin( ak ,bk )
2. Наименьшее общее кратное чисел a и b можно найти
по формуле:
НОК (a, b) p1max( a1 ,b1 ) p2max( a2 ,b2 ) ... pkmax( ak ,bk )
4

5. Алгоритмы разложения на множители

Поиск эффективных алгоритмов для разложения на
множители больших составных чисел ведется давно.
Совершенный алгоритм для этого пока не найден.
Есть несколько алгоритмов, которые могут разложить
число на множители, но ни один не способен провести
разложение достаточно больших чисел в разумное
время.
Это хорошо для криптографии, потому что современные
криптографические системы полагаются на этот факт.
5

6. Методы разложения на множители

Метод проверки делением;
Метод Ферма;
РО (Rho) – метод Полларда
6

7. Метод проверки делением

Самый простой и наименее эффективный алгоритм — метод
разложения на множители проверкой делением.
Чтобы найти делители n, проверяют делимость числа n на все
положительные целые числа от 2 до корня из n.
Алгоритм имеет два цикла: внешний и внутренний.
Внешний
цикл находит уникальные множители в разложении; внутренний
цикл находит повторяющиеся множители разложения.
Пример 1. 24 = 23 х 3. Внешний цикл находит множители 2 и 3.
Внутренний цикл находит, что число 2 трижды входит в разложение.
Пример 2. 1523357784 = 23 х 32 х 13 х 43987.
7

8. Псевдокод для разложения на множители методом проверки делением

Метод проверки делением обычно хорош, если n < 1010, но он
неэффективен и неосуществим для разложения больших
целых чисел. Сложность алгоритма показательна.
8

9. Метод Ферма

Метод Ферма делит число n на два положительных целых числа a и
b (не обязательно простых) так, чтобы n = a x b.
Метод Ферма основан на факте, что если мы можем найти такие
x и y, что n = x2 – y2 = (x + y) (x - y), тогда мы имеем a = x+ y, b = x – y.
Начинаем с наименьшего целого числа х, большего, чем
n
Пробуем найти другое целое число y, такое, чтобы выполнялось
уравнение y2 = x2 – n.
В каждой итерации мы должны рассмотреть, является ли
результат x2 – n полным квадратом. Если мы находим такое
значение для y, мы вычисляем a и b и выходим из цикла.
Иначе мы проводим другую итерацию.
9

10. Псевдокод для разложения на множители по методу Ферма

Сложность метода Ферма является близкой к показательному закону
10

11. Пример 1 разложения на множители методом Ферма

Пусть требуется разложить на множители число 325.
1. Минимальным целым числом, большим 325 является число
х = 19.
2. Для чисел х от 19 до 324 пробуем найти такое целое число y,
чтобы выполнялось равенство y2 = x2 – n .
Для х = 19 имеем: y2 = x2 – n = 192 – 325 = 36 = 62 .
Значит, y = 6 . Следовательно,
n = x2 – y2 = 192 – 62 = (19-6) (19+6) = 13 х 25 = 13 х 52.
11

12. Пример 2 разложения на множители методом Ферма

Пусть требуется разложить на множители число 9424.
1. Минимальным целым числом, большим 9424 является число
х = 98.
2. Для чисел х от 98 до 9424 пробуем найти такое целое число y,
чтобы выполнялось равенство y2 = x2 – n .
Для х = 98 имеем: y2 = x2 – n = 982 – 9424 = 180 (не является
квадратом).
Для х = 99 имеем: y2 = 992 – 9424 = 377 (не является квадратом).
Для х = 100 имеем: y2 = 1002 – 9424 = 576 = 242 . Значит, y = 24 .
Следовательно, n = x2 – y2 = 1002 – 242 = 76 х 124.
12

13. РО (Rho) – метод Полларда

В 1975 г. Джон М. Поллард разработал метод для разложения
на множители, который базируется на следующих
положениях:
a. Предположим, что есть два целых числа x1 и x2, таких, что x1
– x2 делится на p, но не делится на n.
b. Может быть доказано, что p = НОД (x1 – x2, n).
Поскольку x1 – x2 делится на p, можно записать, что
x1 – x2 = q x p . Но поскольку x1 – x2 не делится на n, очевидно,
что q не делится n.
Это означает, что НОД (x1 – x2, n) является либо 1, либо p.
13

14. Алгоритм РО (Rho) метода Полларда

Следующий алгоритм повторно выбирает x1 и x2, пока не находит
соответствующую пару:
1. Выберите x1 — малое случайное целое число, называемое
первоисточником, например, 1.
2. Используйте функцию, чтобы вычислить x2, такую, чтобы x1 – x2 не
делилось на n . Например, x2 = f (x1 ) = x1 2 + a (mod n).
3. Вычислите НОД (x1 – x2 , n) = d. Если d >1, то p = d – искомый
сомножитель. Алгоритм останавливается.
4. Если d =1, то происходит повторение процесса с x1,
x1 = x2 и переход на шаг 2.
14

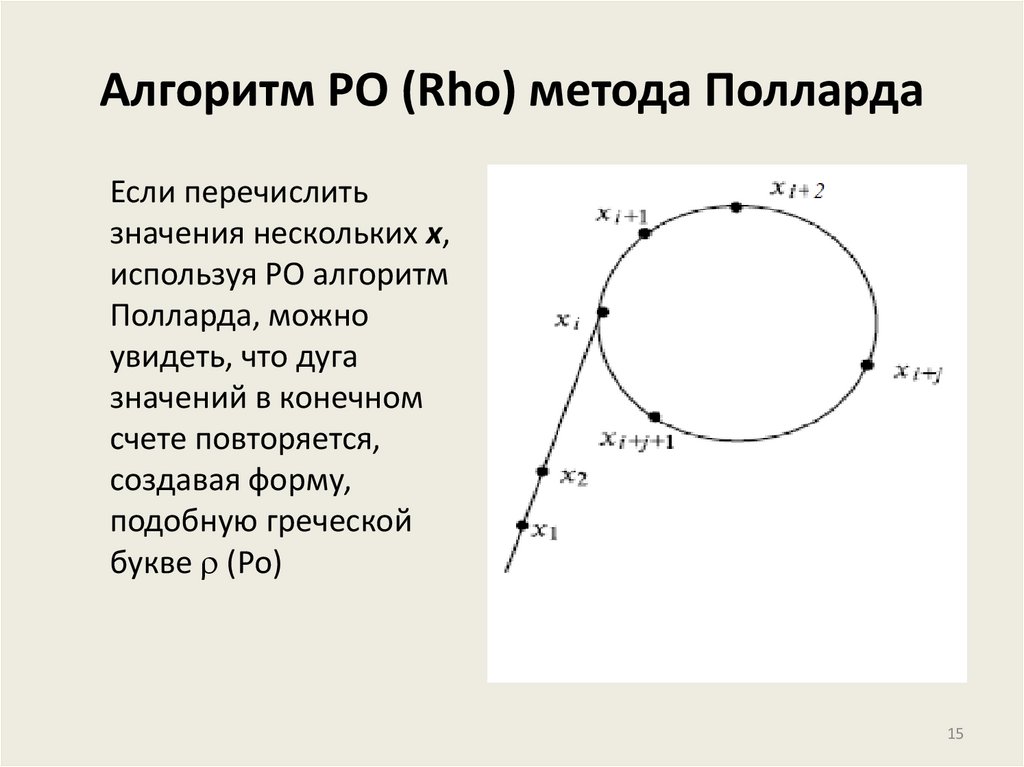
15. Алгоритм РО (Rho) метода Полларда

Если перечислить
значения нескольких x,
используя РО алгоритм
Полларда, можно
увидеть, что дуга
значений в конечном
счете повторяется,
создавая форму,
подобную греческой
букве (Ро)
15

16. Псевдокод для Ро метода Полларда разложения на множители

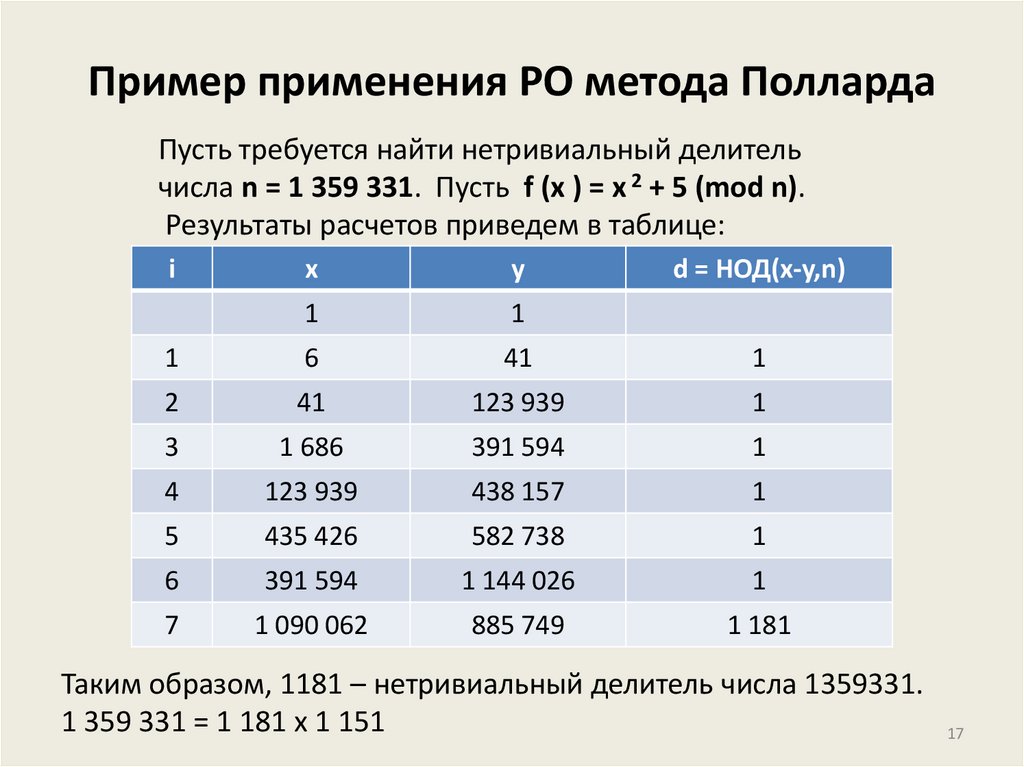
16

17. Пример применения РО метода Полларда

Пусть требуется найти нетривиальный делитель
числа n = 1 359 331. Пусть f (x ) = x 2 + 5 (mod n).
Результаты расчетов приведем в таблице:
i
x
y
d = НОД(x-y,n)
1
1
1
6
41
1
2
41
123 939
1
3
1 686
391 594
1
4
123 939
438 157
1
5
435 426
582 738
1
6
391 594
1 144 026
1
7
1 090 062
885 749
1 181
Таким образом, 1181 – нетривиальный делитель числа 1359331.
1 359 331 = 1 181 х 1 151
17

18. Сложность алгоритма Ро метода Полларда

Предположим, компьютер может выполнить 230 (почти 1
миллиард) разрядных операций в секунду.
Какое время потребуется, чтобы разложить на множители целое
число размера
a. 60 десятичных цифр; b. 100 десятичных цифр?
Множество 60 десятичных цифр имеют почти 200 битов.
Сложность алгоритма 2200/4 = 250. Со скоростью 230 операций в
секунду алгоритм может быть выполнен за 220 секунды или почти
за 12 дней.
b. Множество 100 десятичных цифр — это почти 300 битов.
Сложность — 275. Со скоростью 230 операций в секунду алгоритм
может быть выполнен за 245 секунд или за много лет.
18

19. Китайская теорема об остатках

Китайская теорема об остатках используется, чтобы решить
систему уравнений с одной переменной, но различными
модулями, как это показано ниже:
x a1 (mod m1 )
x a (mod m )
2
2
..................
x ak (mod mk )
Китайская теорема об остатках утверждает, что система
уравнений имеет единственное решение, если модули
являются взаимно простыми.
19

20. Пример 1 китайской теоремы об остатках

Следующий пример содержит систему уравнений с
различными модулями:
x 2(mod 3)
x 3(mod 5)
x 2(mod 7)
Для этой системы уравнений решением является число
= 23.
x
20

21. Решение системы уравнений с модулями

Решение системы уравнений выполняется в следующем порядке:
Найти M = m1 x m2 x … x mk . Это общий модуль.
Найти M1 = M/m1, M2 = M/m2, …., Mk = M/mk.
Используя соответствующие модули m1, m2,…., mk, найти
мультипликативные инверсии M1, M2,…, Mk. Обозначим их через
M1-1, M2-1,…, Mk-1.
Решение системы уравнений находится по формуле:
x = (a1 x M1 x M1-1 + a2 x M2 x M2-1 + … +ak x Mk x Mk-1 ) mod M
21

22. Пример решения китайской теоремы об остатках

Найдите решение системы уравнений
x 2(mod 3)
x 3(mod 5)
x 2(mod 7)
M= 3 x 5 x 7 =105
M1 = 105 / 3 = 35, M2 = 105 / 5 =21, M3 = 105 / 7 = 15
M1-1 = 2 (mod 3), M2-1 = 1 (mod 5), M3-1 = 1 (mod 7).
х = 2 x 35 x 2 + 3 x 21 x 1 +2 x 15 x 1 = 233 23 (mod 105).
22

23. Пример 2 китайской теоремы об остатках

Найти целое число, которое дает в остатке 3, если его
разделить на 7 и 13, но без остатка делится на 12.
Это проблема китайской теоремы об остатках. Мы можем
составить три уравнения и найти значение x.
x 3(mod 7)
x 3(mod13)
x 0(mod12)
Для этой системы уравнений решением является число
= 276.
x
23

24. Обзорные вопросы по лекции 5

• 1. Сформулируйте основную теорему арифметики.
• 2. Перечислите методы разложения на множители. Какой из
методов раскладывает число на простые множители?
• 3. Объясните суть алгоритма разложения на множители
проверкой делением.
• 4. На каком факте основан метод Ферма разложения на
множители?
• 5. Объясните основные шаги алгоритма разложения на
множители методом Ферма.
• 6. На каком положении базируется РО (Rho) – метод Полларда?
• 7. Какова сложность алгоритма Ро метода Полларда?
• 8. Сформулируйте китайскую теорему об остатках.
24