Формулы для решения С2 координатно-векторным способом

1.

ФОРМУЛЫ
ДЛЯ РЕШЕНИЯ ЗАДАНИЙ
С2
КООРДИНАТНО - ВЕКТОРНЫМ
СПОСОБОМ
г. Новороссийск
МОУ СОШ № 10
учитель математики
Волкова О.А.

2.

СОДЕРЖАНИЕ
НУЖНЫЕ
ФОРМУЛЫ
УГЛЫ в ПРОСТРАНСТВЕ
РАССТОЯНИЕ в ПРОСТРАНСТВЕ
ПРИМЕРЫ ПРИМЕНЕНИЯ ФОРМУЛ

3.

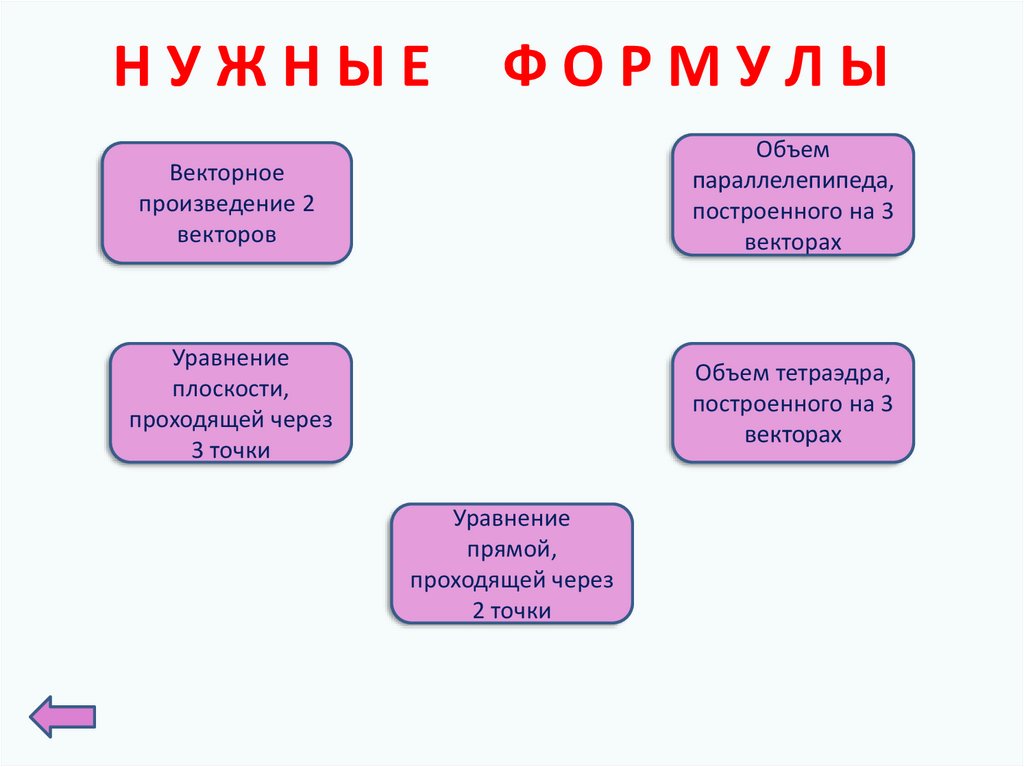
НУЖНЫЕ
ФОРМУЛЫ
Векторное
произведение 2
векторов
Объем
параллелепипеда,
построенного на 3
векторах
Уравнение
плоскости,
проходящей через
3 точки
Объем тетраэдра,
построенного на 3
векторах
Уравнение
прямой,
проходящей через
2 точки

4.

ВЕКТОРНОЕ
ПРОИЗВЕДЕНИЕ
2)
D
M
A
B
=
,
∙
3)
∙

5.

У Р А В Н Е Н И Е П Л О С К О С Т И, П Р О Х О Д Я Щ Е Й Ч Е Р Е З
M1(x1 ; у1 ; z1)
M2(x2 ; у2 ; z2)
M3(x3 ; у3 ; z3)
3
ТОЧКИ

6.

Объем параллелепипеда, построенного на 3 векторах
D
A
B
V = mod

7.

ОБЪЕМ
A
Т Е Т Р А Э Д Р А, П О С Т Р О Е Н Н О Г О на 3 векторах
B
V=

8.

У Р А В Н Е Н И Е П Р Я М О Й, П Р О Х О Д Я Щ Е Й через 2 точки
М1М2 {x2 –x1; y2 –y1; z2 –z1}
M(x ; у ; z)
{x –x1; y –y1; z –z1}
M2(x2 ; у2 ; z2)
M1(x1 ; у1 ; z1)
M1
M1
M2
M
=
=

9.

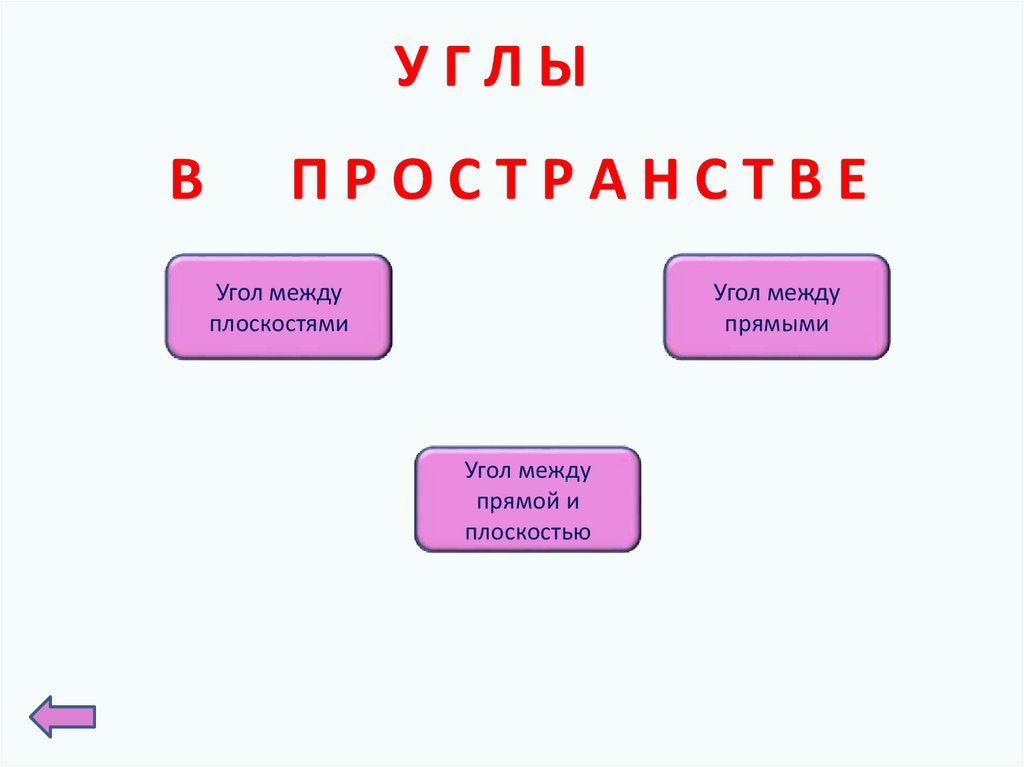
УГЛЫ
В
ПРОСТРАНСТВЕ
Угол между
плоскостями
Угол между
прямыми
Угол между
прямой и
плоскостью

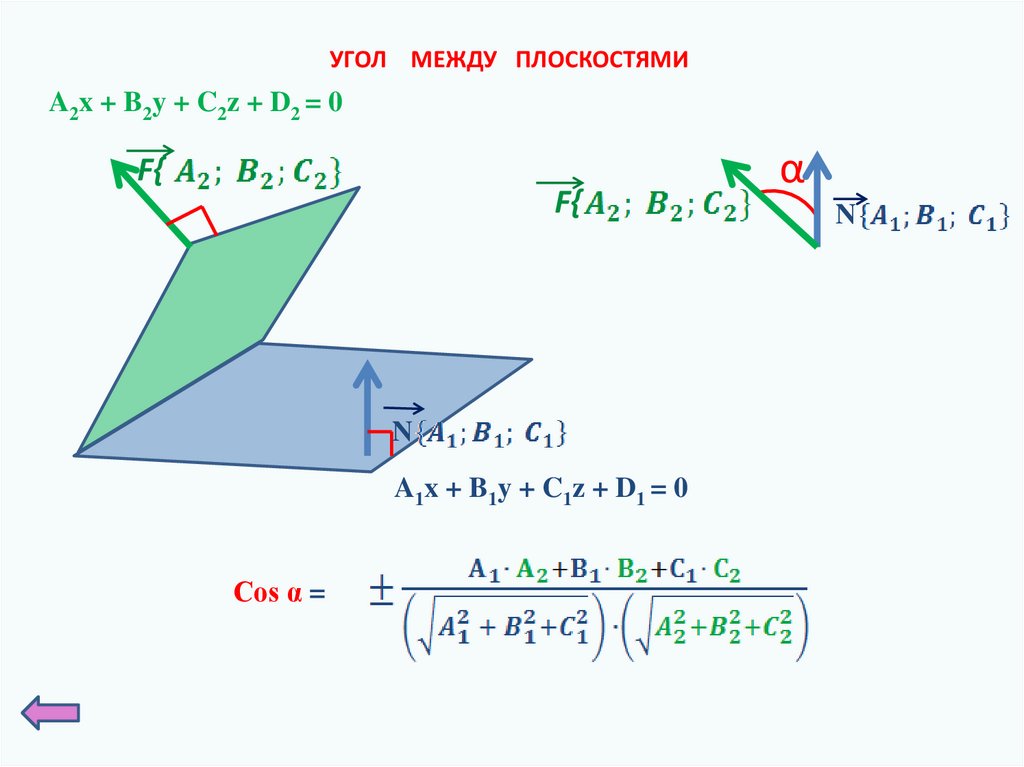
10.

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
A2x + B2y + C2z + D2 = 0
F{
F{
N
A1x + B1y + C1z + D1 = 0
Cos α =
α
N

11.

УГОЛ МЕЖДУ ПРЯМЫМИ
b
b
=
=
α
M2(x2 ; у2 ; z2)
a
M1(x1 ; у1 ; z1)
=
a
Cos α =
=

12.

УГОЛ МЕЖДУ ПРЯМОЙ и ПЛОСКОСТЬЮ
b
N
β
b
=
=
α
M2(x2 ; у2 ; z2)
α
N
A1x + B1y + C1z + D1 = 0
=
=

13.

РАССТОЯНИЕ
В
ПРОСТРАНСТВЕ
Расстояние
между 2
точками
Расстояние между
скрещивающимися
прямыми
Расстояние от
точки до прямой
Расстояние от
точки до
плоскости

14.

РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ
M2(x2 ; у2 ; z2)
M1(x1 ; у1 ; z1)

15.

Р А С С Т О Я Н И Е от Т О Ч К И до П Р Я М О Й
M2(x2 ; у2 ; z2)
!
d=h=
h
M1(x1 ; у1 ; z1)
a
=
2)
=
1) М1М2 {x2 – x1; y2
– y1 ; z2 – z1 }
а × М1М2 =
3)
4)
5)
d =

16.

РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
b
=
=
M2(x2 ; у2 ; z2)
=
1)
a
M1(x1 ; у1 ; z1)
=
2)
=
=
3)
mod

17.

Р А С С Т О Я Н И Е от Т О Ч К И до П Л О С К О С Т И
M2(x2 ; у2 ; z2)
d
N
A1x + B1y + C1z + D1 = 0

18.

ПРИМЕРЫ ПРИМЕНЕНИЯ ФОРМУЛ
РЕШЕНИЕ ТИПОВЫХ
ЗАДАЧ
РЕШЕНИЕ ЗАДАЧ ДВУМЯ
СПОСОБАМИ

19.

1. Найти векторное произведение векторов
и его модуль
и
=
×
=
= 1∙3 +2∙2 + 5∙1 -1∙3 - 2∙5 -1∙2 =
= -7
=
=
+3 +
=

20.

СОСТАВИТЬ УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ТОЧКИ
M1(2;2;2)
1)
M2(4;0;3 )
M3(0;1;0)
2)
3) 4(x-2) – 2(z-2) -2(y-2) -4(z-2) +1(x-2) +4(y-2) =0
5x + 2y -6z -2 = 0
нормаль

21.

Найти объем параллелепипеда ABCDA1B1C1D1 , если
V=
=
=15 +4 + 6 + 12+2- 15 = 24
=

22.

У Р А В Н Е Н И Е ПР Я М О Й, П Р О Х О Д Я Щ Е Й
ЧЕРЕЗ 2 ТОЧКИ

23.

НАЙТИ УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
4x - 5y + 3z - 1 = 0
x - 4y - z + 9 = 0
= 0,7
α = arccos 0,7

24.

НАЙТИ УГОЛ МЕЖДУ ПРЯМЫМИ

25.

НАЙТИ
УГОЛ МЕЖДУ ПРЯМОЙ и ПЛОСКОСТЬЮ
2x+y-z +4 = 0
=

26.

Н А Й Т И Р А С С Т О Я Н И Е от Т О Ч К И до П Р Я М О Й
2)
4)
3)
=

27.

РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
A(1;3;-1)
O(0;0;0)

28.

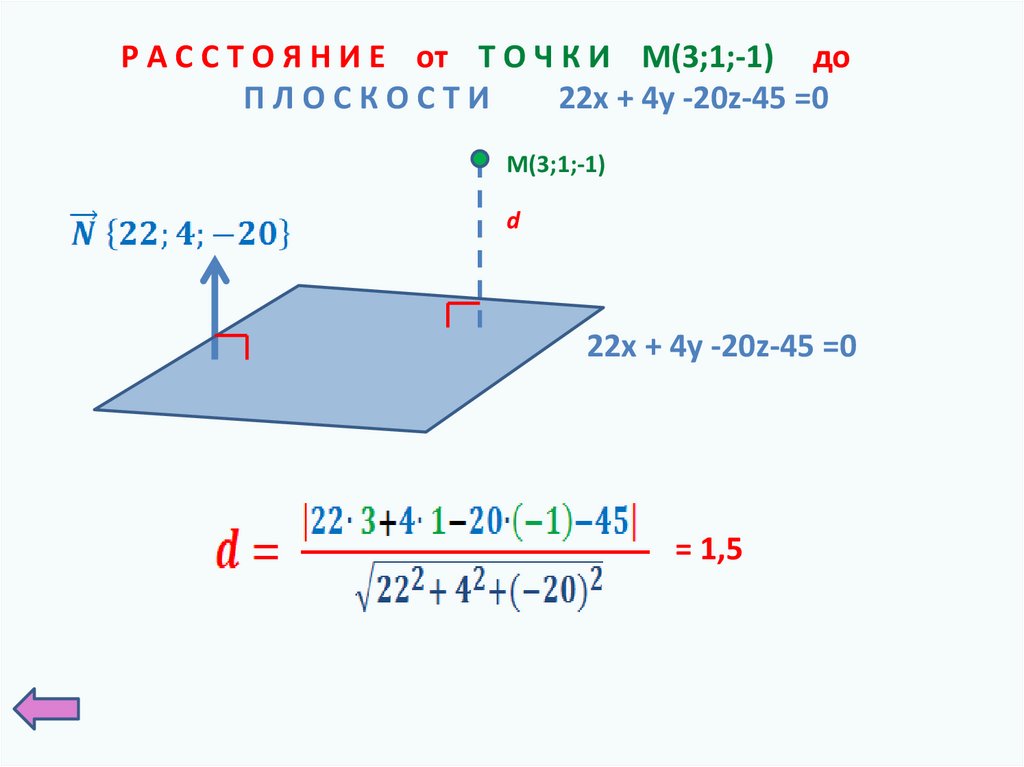
Р А С С Т О Я Н И Е от Т О Ч К И M(3;1;-1) до
ПЛОСКОСТИ
22x + 4y -20z-45 =0
M(3;1;-1)
d
22x + 4y -20z-45 =0
= 1,5

29.

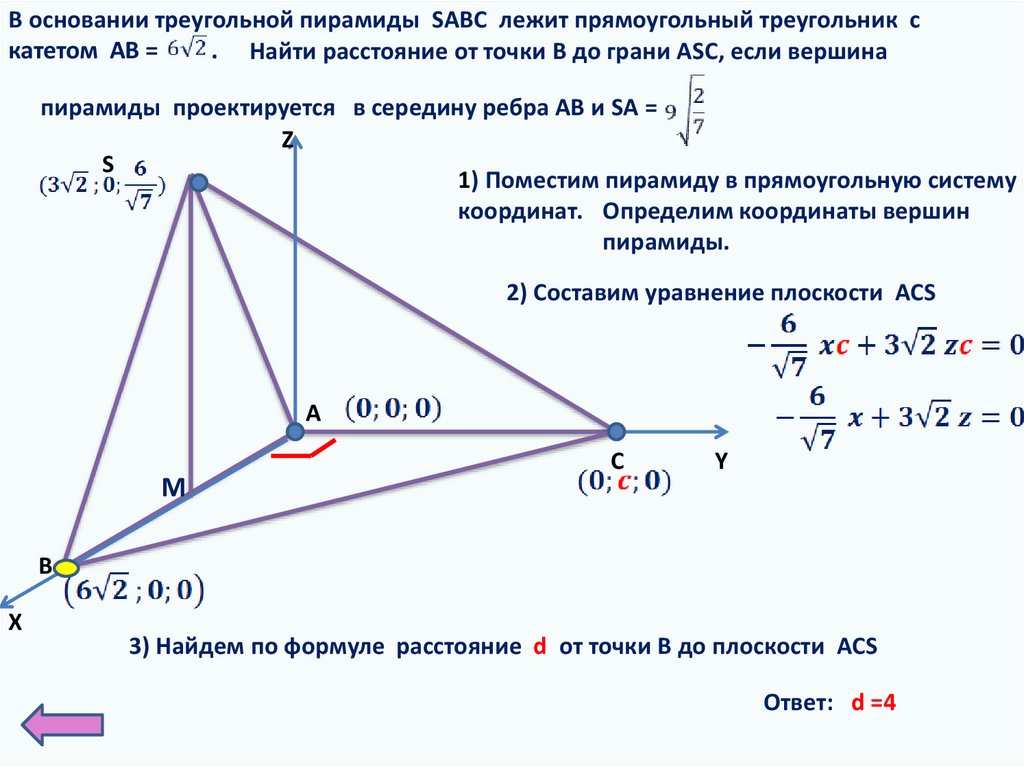
В основании треугольной пирамиды SABC лежит прямоугольный треугольник с
катетом АВ =
. Найти расстояние от точки В до грани ASC, если вершина
пирамиды проектируется в середину ребра АВ и SA =
Z
S
1) Поместим пирамиду в прямоугольную систему
координат. Определим координаты вершин
пирамиды.
2) Составим уравнение плоскости ACS
A
M
C
Y
B
X
3) Найдем по формуле расстояние d от точки В до плоскости ACS
Ответ: d =4

30.

В кубе ABCDA1B1C1D1 с ребром АВ = 3 найти расстояние между диагоналями AB1 и BD
C1
B1
A1
O2
O2
C1
D1
A1
O
О1
O1
α
B
B2
C
О3
A
D
1) B2D2 II BD,
B2D2
AC
1
A
D2
β
O3
C
3)
A1C
A1C
BD
2) A1O2 = O2C1 =AO3 = O3C = 1,5
A1O = OO1 = O1C =
4) A1C
O3C1
A1C
BD
A1C
(BDC1)
A1C
(B1D1A)
O3C1

31.

В кубе ABCDA1B1C1D1 с ребром АВ = 3 найти расстояние между диагоналями AB1 и BD
Y
Z (0;0;3)
C1
B1
C(0;3;0)
D(3;3;0)
1)
D1
A1
B(0;0;0)
B
C Y
2)
A
D
X
4)
3)
5)
A(3;0;0)
X

32.

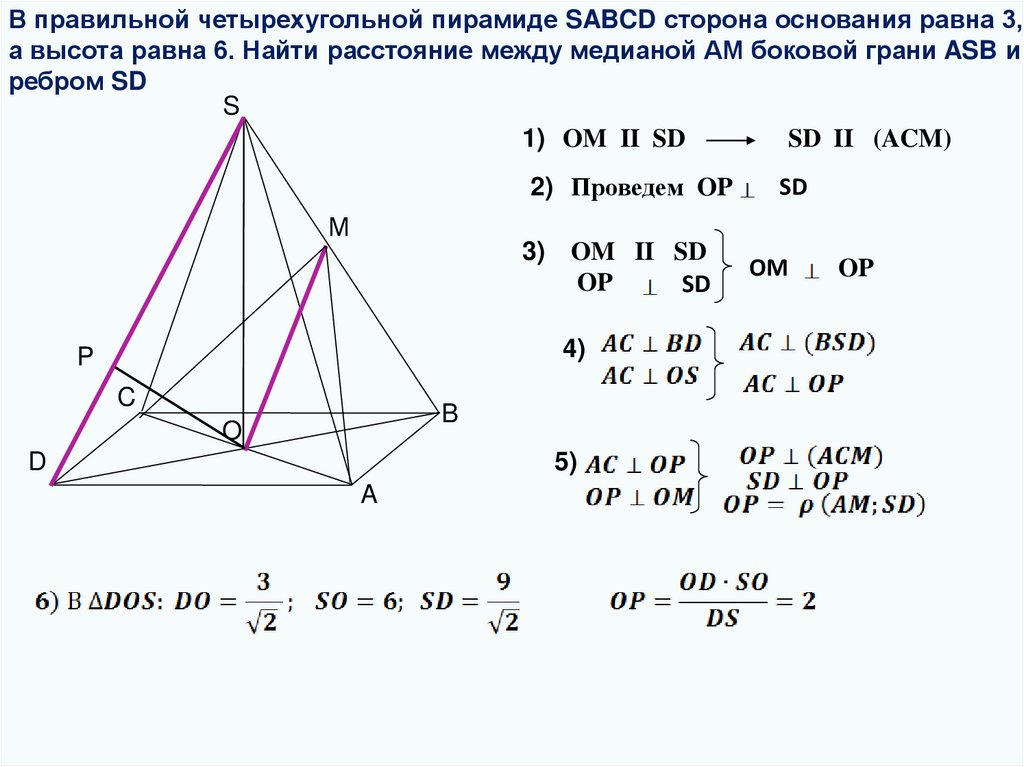
В правильной четырехугольной пирамиде SABCD сторона основания равна 3,
а высота равна 6. Найти расстояние между медианой АМ боковой грани ASB и
ребром SD
S
1) OM II SD
SD II (ACM)
2) Проведем OP
SD
М
3)
OM II SD
OP
SD
4)
P
C
B
O
D
5)
A
OM
OP

33.

В правильной четырехугольной пирамиде SABCD сторона основания равна 3,
а высота равна 6. Найти расстояние между медианой АМ боковой грани ASB и
ребром SD
Y C(0;3;0)
D(3;3;0)
S
Z
1)
M1
М
B(0;0;0)
O
O(1,5;1,5;0)
A(3;0;0)
X
M1(0,75;0,75;0) M(0,75;0,75;3) S(1,5;1,5;6)
Y
C
O
D
B
M1
A
X
=2