Теория массового обслуживания (3)

1. Моделирование систем массового обслуживания

2. Введение

В реальной жизни : пребывание в состоянии
ожидания
очередь покупателей у касс большого магазина
группа пассажирских самолетов, ожидающих
взлет в аэропорте
ряд вышедших из строя станков и механизмов,
поставленных в очередь для ремонта

3. Сократить время ожидания до какого-то терпимого предела

Ожидание – прямое следствие
вероятностного характера возникновения
потребности в том или ином виде
обслуживания и разброса показателей
соответствующих обслуживающих
систем.
(заранее не известны ни время
возникновения потребностей, ни
продолжительность обслуживания)

4. Цель анализа систем массового обслуживания

Нахождение количественных показателей
функционирования систем массового
обслуживания:
Среднее время пребывания заявки
пребывания в очереди на обслуживание
(оценка системы с позиции “клиента”)
Доля времени, в течение которой система
простаивает (оценка системы с точки
зрения ее загруженности)

5. Зависимость между требованиями “клиентов” и мощностью (операционной возможностью) обслуживающей системы

время
ожидания
заявки в
очереди на
обслуживание
Теория вероятностей
Теория случайных процессов
доля времени
простаивания
системы
облуживания

6. Каналы обслуживания

Любая система массового обслуживания
состоит из определенного числа
обслуживающих единиц – каналов
обслуживания
(станки, приборы, компьютеры, станции,
машины)

7.

Заявки на обслуживание в СМО поступают
нерегулярно (случайно) и образуют поток
заявок или требований
СМО с отказами
СМО с ожиданием
(очередью)
Заявка, поступающая в
момент, когда все каналы Заявка, пришедшая в
момент, когда все
заняты, получает отказ,
покидает СМО и в
каналы заняты, не
дальнейшем в процессе
уходит, а
обслуживания не
становится в
участвует
очередь на
обслуживание
телефонная сеть

8. Классификация СМО с отказами

Классификация систем массового
обслуживания (СМО) по количеству
каналов обслуживания:
одноканальные
СМО
многоканальные
СМО
Классификация СМО с отказами
одноканальная
СМО с отказами
многоканальная
СМО с отказами

9. Классификация СМО с ожиданием (очередью)

Одноканальная СМО с неограниченной
длиной ожидания
Многоканальная СМО с
неограниченной очередью
СМО с ограниченной очередью
СМО с ограниченным временем
ожидания

10. Дисциплина обслуживания

определяет порядок выбора заявок из
числа поступивших и порядок их
распределения между свободными
каналами.
Принципы обслуживания требования:
1) “первый пришел – первый обслужен”
2) “первый пришел – последний обслужен”
(отгрузка однородной продукции со склада)

11. 3) Обслуживание с приоритетом

Абсолютный приоритет.
более важная заявка вытесняет из
обслуживания обычную заявку в любом
случае
Относительный приоритет
важная заявка получает лишь ”лучшее”
место в очереди

12. Случайный (стохастический, вероятностный) процесс

процесс изменения во времени состояния какой-
либо системы в соответствии с вероятностным
законом
Работа СМО представляет собой случайный
процесс с дискретными состояниями и
непрерывным временем.
состояние СМО меняется скачком в случайные
моменты появления событий
(появление новой заявки, приоритета обслуживания,
окончания обслуживания)

13.

В процессе с дискретными состояниями
возможные состояния
S1 , S 2 , S 3 ,...S n ,...
можно заранее перечислить, а переход
системы из состояния в состояние
происходит мгновенно

14.

В процессе с непрерывным временем
моменты возможных переходов системы из
состояния в состояние не фиксированы
заранее, а являются случайными

15. Марковский процесс (случайный процесс без последействий)

В Марковском случайном процессе,
протекающем в системе
для любого момента времени t0
вероятностные характеристики
процесса в будущем зависят только от
его состояния в данный момент t0 и
не зависят от того, когда и как система
пришла в это состояние.

16. Пример Марковского процесса

Система S – счетчик пройденного
автомобилем расстояния. Состояние
системы в момент t характеризуется числом
километров, пройденных автомобилем до
данного момента
Пусть в момент времени to счетчик
показывает So. Вероятность того, что в
момент t>to счетчик покажет то или иное
число километров S1, зависит только So, но
не зависит от того, каким были показатели
счетчика до момента to.

17. Процесс гибели и размножения

математическая модель изменения
численности популяций
если все состояния системы пронумеровать
S 0 , S1 ,...S k ,...S n
то из состояния S k
состояние
(k<n) можно попасть либо в
S k l либо в состояние S k l

18. Поток событий

-
последовательность однородных
событий, следующих одно за другим в
какие-то случайные моменты времени
- поток вызовов на телефонной станции
- поток неисправностей подвижного состава

19. Разновидности потоков

регулярный поток
стационарный поток
поток без последействия
ординарный поток
простейший (стационарный
пуассоновский) поток
рекуррентный поток (Пальма)
поток Эрланга

20. Регулярный поток событий

события следуют одно за другим
через определенные равные
промежутки времени
На практике - потоки не регулярные, со
случайными интервалами.

21. Стационарный поток событий

его вероятностные характеристики не
зависят от времени
поток вызовов на АТС между 13 и 14
часами, практически стационарен; тот же
поток в течение суток не стационарен.

22. Поток событий без последействия

для любых двух непересекающихся участков
времени и число событий, попадающих на
один из них, не зависит от того, сколько
событий попало на другой.
(События, образующие поток, появляются в
те или иные моменты времени независимо
друг от друга, вызванные каждое своими
собственными причинами)

23. Ординарный поток событий

события появляются поодиночке, а не
группами по несколько сразу
если поток событий ординарен, то
вероятностью попадания на малый
участок времени двух или более событий
можно пренебречь.

24. Простейший (стационарный пуассоновский) поток событий

стационарный, ординарный и без
последействия
При наложении достаточно большого числа
независимых, стационарных и ординарных
потоков получается поток, близкий к
простейшему.

25. Рекуррентный поток событий (поток Пальма)

Стационарный, ординарный, с
интервалами времени между событиями,
представляющими независимые
случайные величины с одинаковым
произвольным распределением

26. Поток Эрланга

Пусть в какое-то учреждение поступает
простейший поток посетителей, у входа
стоит управляющий очередью,
направляющий первого посетителя к
первому столу, второго – ко второму
столу и т.д.
Если столов - n, то на каждый из них
поступает поток Эрланга n-го порядка.
Простейший поток - поток Эрланга первого
порядка

27. Коэффициент вариации интервалов между событиями потока Эрланга

При таком просеивании простейшего потока
коэффициент вариации интервалов уменьшается и
поток Эрланга приближается к регулярному.
Коэффициент вариации интервалов между
событиями потока Эрланга n-го порядка равен
vT( n)
1
n
Потоки Эрланга образуют гамму потоков с различной
степенью упорядоченности – от «полного беспорядка»
(простейший поток) до полной упорядоченности (регулярный
поток).

28.

Интенсивность потока
среднее число событий приходящееся на
единицу времени
- постоянная величина ( const )
- переменная величина (зависит от
времени)

29. Простейший поток с интенсивностью

интервал T между соседними событиями имеет
показательное распределение с плотностью:
f (t ) e t , t 0
Величина
- параметр показательного закона.
Для случайной величины Tимеющей показательное
распределение, математическое ожидание
Mесть
T
величина, обратная параметру, а среднее
квадратическое отклонение
равно
математическому ожиданию: T
1
MT T

30. Коэффициент вариации

Коэффициент вариации интервалов между событиями
для показательного распределения
vT
T
MT
1
Для регулярного потока событий, у которого интервал
vT 0
между событиями не случаен
Чем ближе
Простейший поток – это «наименее регулярный» из
встречающихся на практике потоков
к нулю, тем «регулярнее» поток
vT

31. Элемент вероятности

Рассмотрим на оси Ot простейший поток с
интенсивностью и произвольно
расположенный элементарный участок
времени t .
Элемент вероятности
-
вероятность попадания на этот участок
хотя бы одного события потока.
P t t

32. Марковские процессы с дискретными состояниями и непрерывным временем

удобно представлять, что все переходы
системы из состояния в состояние
происходят под действием каких-то потоков
событий.
Если все потоки событий, переводящие
систему из состояния в состояние, простейшие, то процесс, протекающий в
системе, Марковский.

33. Уравнения Колмогорова для вероятностей состояний

Если система
S находится в каком-то
состоянии Si, из которого есть
непосредственный переход в другое
состояние Sj, то на систему, пока она
находится в состоянии Si, действует
простейший поток событий. Как только
появится первое состояние этого потока,
происходит переход системы из Si в Sj.

34. Уравнения Колмогорова для вероятностей состояний

Обозначим
ij
интенсивность потока
событий, переводящего систему из
состояния Si в Sj.
По графу состояний системы строим
математическую модель процесса

35.

Уравнения Колмогорова для
вероятностей состояний
Пусть система S имеет n различных состояний
S1 , S 2 , , S n
pi (t )
- вероятность i-го состояния, вероятность того,
что в момент t система будет находиться в состоянии
Si.
Для любого момента сумма всех
n вероятностей
состояний равна единице:
pi (t ) 1
i 1
По графу состояний, можно найти все вероятности
pi (t )
состояний как функции времени.

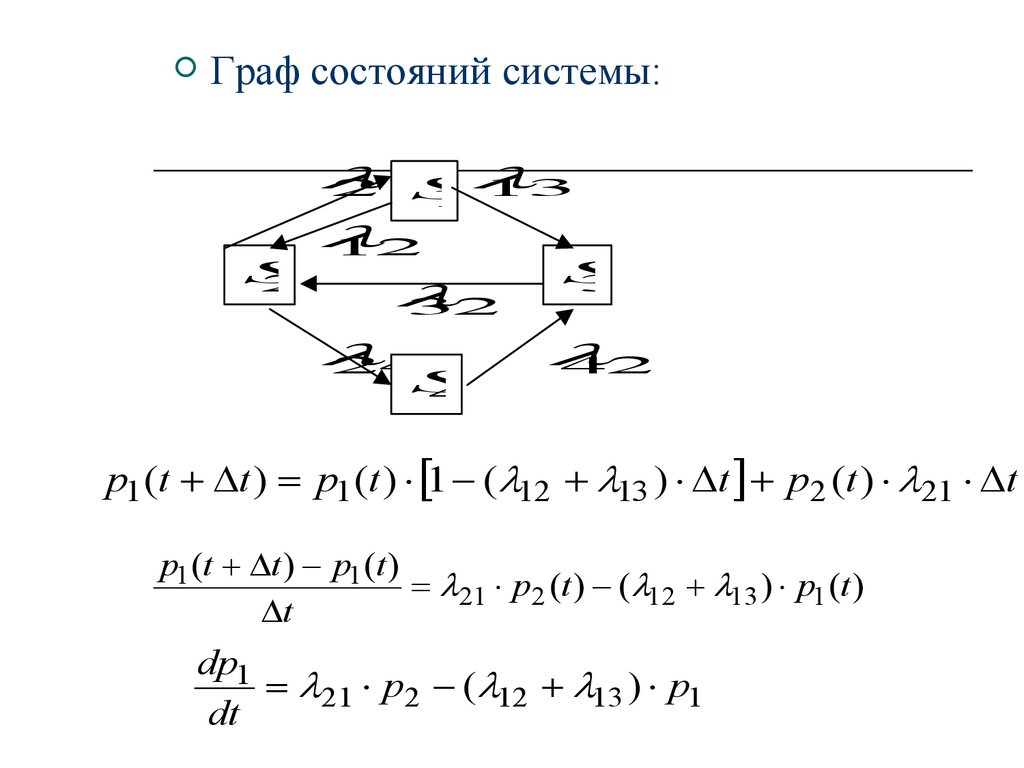
36.

Граф состояний системы:
21
S
1 13
12
S
S
2
3
32
24
42
S
4
p1 (t t ) p1 (t ) 1 ( 12 13 ) t p2 (t ) 21 t
p1 (t t ) p1 (t )
21 p2 (t ) ( 12 13 ) p1 (t )
t
dp1
21 p2 ( 12 13 ) p1
dt

37.

Уравнения Колмогорова дают возможность найти
все вероятности состояний как функции времени
dp1
p
(
)
p
21
2
12
13
1
dt
dp2 p p ( ) p
12
1
32
3
24
21
2
dt
dp3 p p p
13 1
43
4
32
3
dt
dp
4 24 p2 43 p4
dt

38. Финальные вероятности

Финальная вероятность
- среднее относительное время пребывания
системы в конкретном состоянии

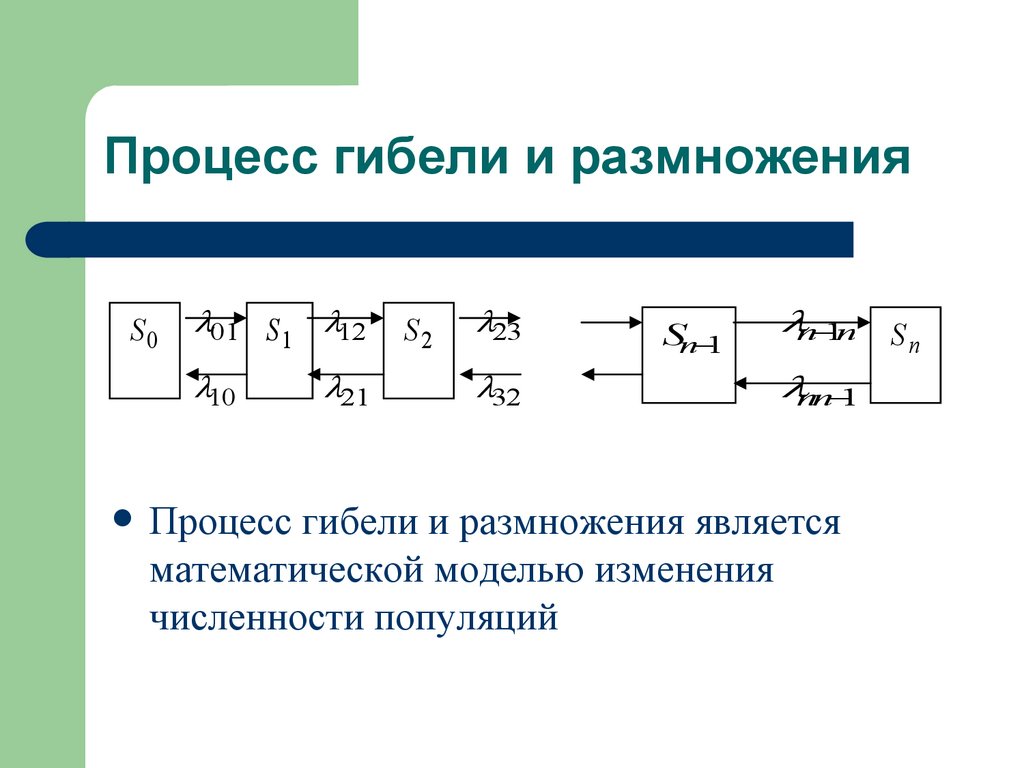
39. Процесс гибели и размножения

S0
01 S 1 12
10
21
S2
23
Sn 1
32
n 1n S
n
nn 1
Процесс гибели и размножения является
математической моделью изменения
численности популяций

40. Рассмотрим упорядоченное множество состояний S0, S1, S2, …Sn

Из любого состояния переходы могут
осуществляться только в состояния с
соседними номерами:
Sk+1
k<n
Sk
Sk-1
Все потоки событий, переводящие систему
по стрелкам из состояния в состояние –
простейшие с соответствующими
интенсивностями

41. Финальные вероятности процесса гибели и размножения

10
01
p
p0
1
12
01
12
p
p
p
2
1
0
21 10
21
01
12
n
1
n
p
p
n
0
10
21 n
n
1
01 01 12
01 12 n 1 n
p0 1
10 10 21
10
21
n
n
1
1

42. Системы массового обслуживания с отказами

Одноканальная система с
отказами
Многоканальная система с
отказами (Задача Эрланга)

43. Показатели эффективности СМО с отказами

А – абсолютная пропускная способность
СМО – среднее число заявок,
обслуживаемых в единицу времени
Q – относительная пропускная
способность – средняя доля пришедших
заявок, обслуживаемых системой
Pотк – вероятность отказа – заявка
покинет СМО не обслуженной
kср – среднее число занятых каналов
(многоканальная СМО)

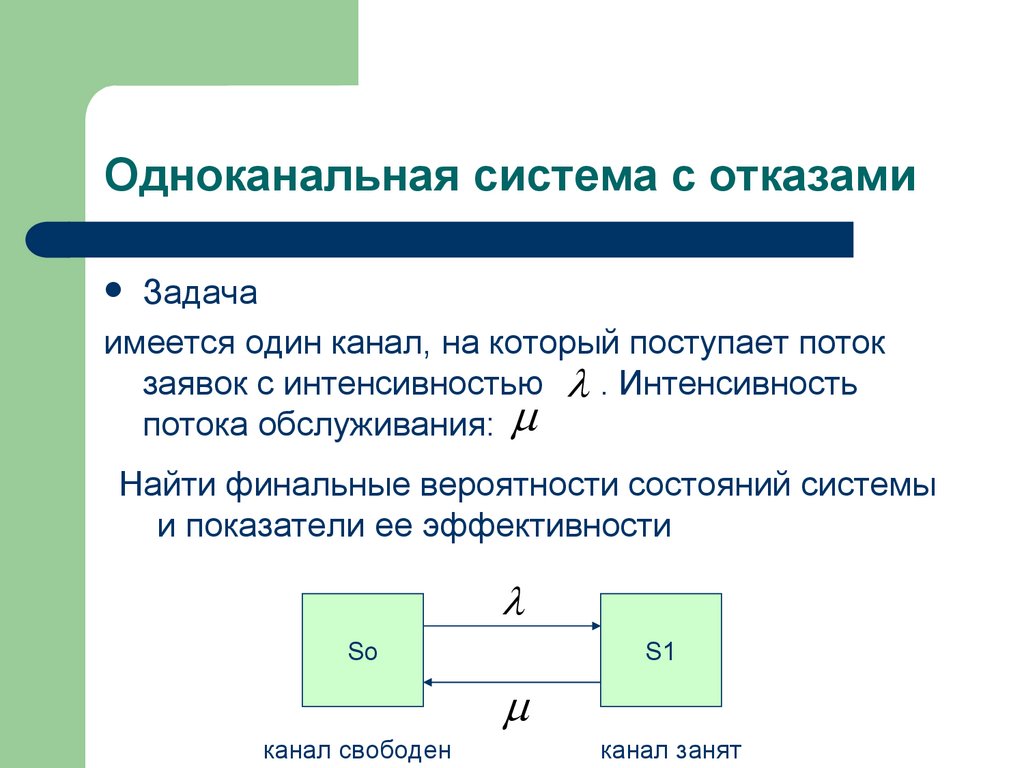
44. Одноканальная система с отказами

Задача
имеется один канал, на который поступает поток
заявок с интенсивностью . Интенсивность
потока обслуживания:
Найти финальные вероятности состояний системы
и показатели ее эффективности
So
S1
канал свободен
канал занят

45. Финальные вероятности состояний системы

p0
среднее относительное
время пребывания
системы в состоянии Sо
(канал свободен)
пропускная способность
Q
p1
среднее относительное
время пребывания
системы в состоянии
S1 (канал занят)
вероятность отказа
Pотк

46. Показатели эффективности системы

Q
Pотк
относитель ная
пропускная способност ь
вероятность отказа
A
абсолютная пропускная способность =
относительная пропускная способность *
• интенсивность потока заявок

47. Многоканальная система массового обслуживания с отказами Задача Эрланга

Поток обслуживаний
- поток заявок, обслуживаемых одним непрерывно
занятым каналом.
Задача Эрланга
имеется n каналов, на которые поступает поток
заявок с интенсивностью
1
Поток обслуживаний имеет интенсивность
tоб
(tоб – среднее время обслуживания)
Найти финальные вероятности состояний системы
и характеристики ее эффективности

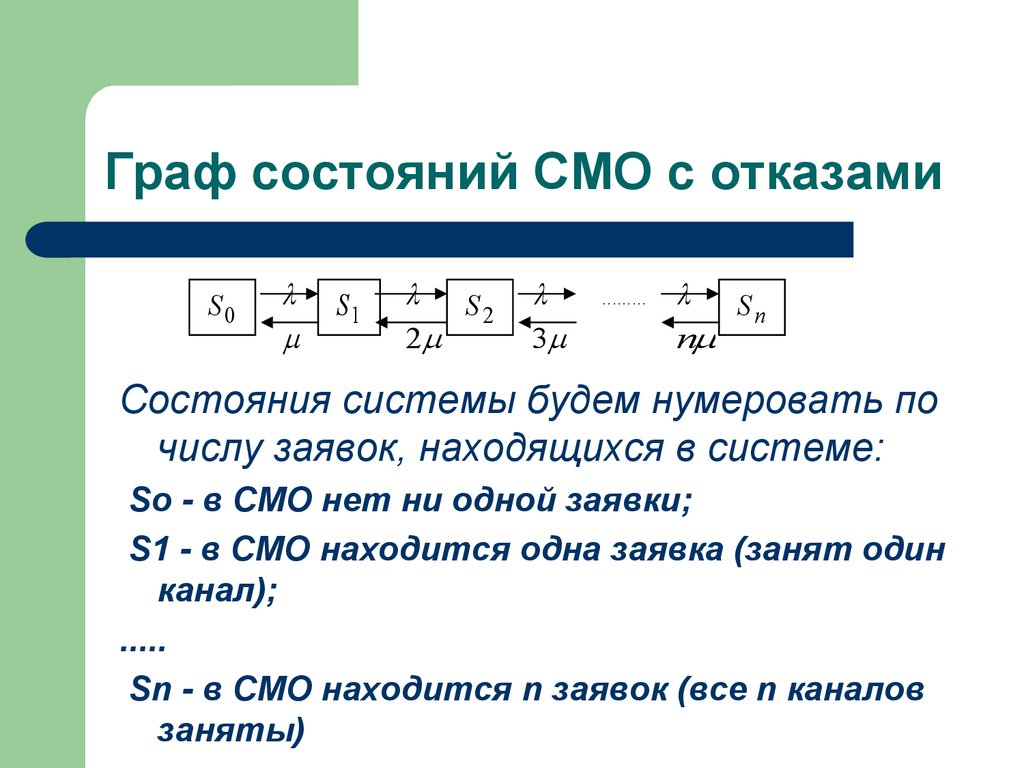
48. Граф состояний СМО с отказами

S0
S1
S2
2
3
.........
Sn
n
Состояния системы будем нумеровать по
числу заявок, находящихся в системе:
So - в СМО нет ни одной заявки;
S1 - в СМО находится одна заявка (занят один
канал);
.....
Sn - в СМО находится n заявок (все n каналов
заняты)

49. Финальные вероятности состояний системы

используем формулы финальных вероятностей в
схеме гибели и размножения
p1 p0
2
p2
p
0
2
2
n
pn
p0
n
n!
p0 1 2
3
n
2
2
3
n
!
2
3
n
1

50. Формулы для финальных вероятностей – формулы Эрланга

приведенная интенсивность потока заявок
(среднее число заявок, приходящее за среднее
время обслуживания одной заявки)
p1 p0
p2
2
2!
p0
pn
n 1
p0 1
2
!
3
!
n
!
2
3
n
n!
p0

51. Характеристики эффективности

вероятность отказа
- все каналы
будут заняты
n
Pотк pn
p0
n!
относительная пропускная способность
Q 1 Pотк 1
n
n!
p0
абсолютная пропускная способность
n
A Q 1
p0
n
!

52. Характеристики эффективности

среднее число занятых каналов
- математическое ожидание дискретной
случайной величины с возможными
значениями 0, 1, 2, ... n и вероятностями
эти значений p0 , p1 , , pn :
n
k 0 p0 1 p1 2 p2 n pn 1
p0
n
!

53. Системы массового обслуживания с ожиданием

Одноканальная система с
неограниченной очередью
Многоканальная система с
неограниченной очередью
Система МО с ограниченной
очередью
Система МО с ограниченным
временем ожидания

54. Показатели эффективности СМО с ожиданием

А – абсолютная пропускная способность
СМО – среднее число заявок,
обслуживаемых в единицу времени
Q – относительная пропускная
способность – средняя доля пришедших
заявок, обслуживаемых системой
Pотк – вероятность отказа – заявка
покинет СМО не обслуженной
kср – среднее число занятых каналов
(многоканальная СМО)

55. Показатели эффективности СМО с ожиданием

Lсист - среднее число заявок в системе
(обслуживаемых или стоящих в очереди)
Wсист - среднее время пребывания заявки
Lоч
в системе
- среднее число заявок в очереди
(длина очереди)
- среднее время пребывания
Wоч
заявки в очереди
- вероятность того, что канал занят
Pзан
(степень загрузки канала)

56. Формула Литтла

Рассмотрим любую систему массового
обслуживания и связанные с нею два потока
событий:
- поток заявок, прибывающих в СМО
- поток заявок, покидающих СМО
Если в системе установился стационарный режим,
то среднее число заявок, прибывающих в СМО за
единицу времени, равно среднему числу заявок,
покидающих ее:
оба потока имеют одну и ту же интенсивность.

57. Формула Литтла

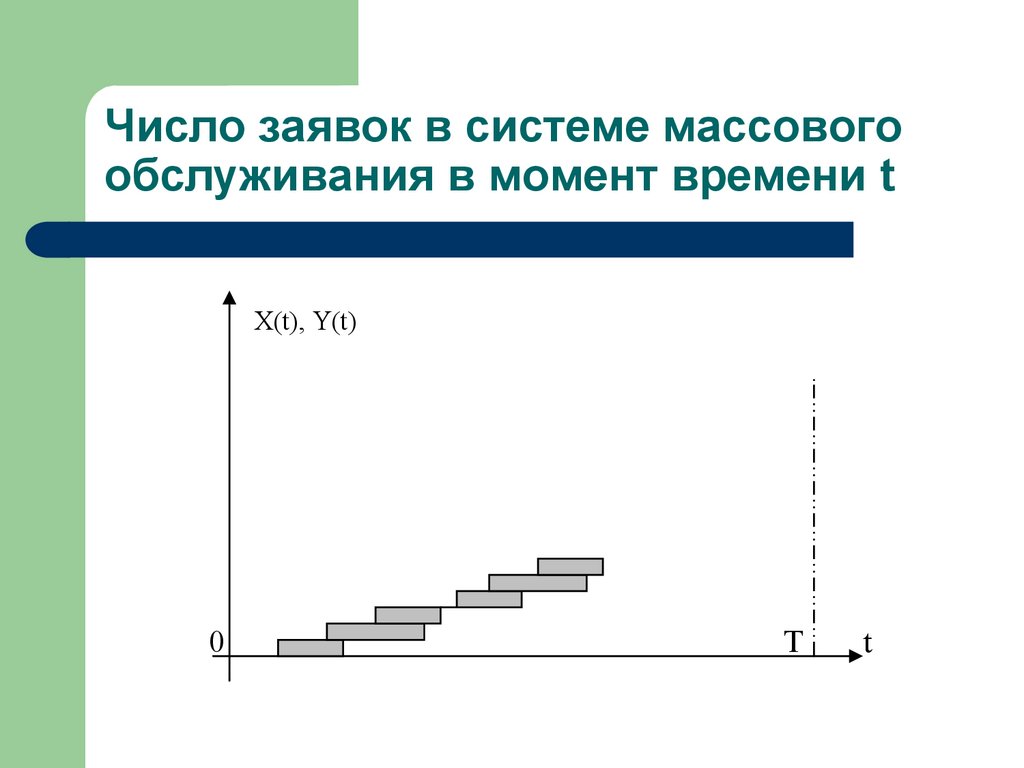
X (t ) - число заявок, прибывших в СМО до
момента t
Y (t ) - число заявок, покинувших СМО до
момента t
Обе функции являются случайными и меняются
скачком в моменты приходов и уходов заявок

58. Число заявок в системе массового обслуживания в момент времени t

X(t), Y(t)
0
T
t

59. Формула Литтла

Функция
Z (t ) X (t ) Y (t ) - число заявок,
находящихся в очереди
Рассмотрим очень большой промежуток
времени T и вычислим для него среднее
число заявок, находящихся в СМО:
T
1
Lсист Z (t )dt
T0

60. Формула Литтла

при достаточно больших T, можно
считать, что
T
Z (t )dt t
i
i
0
где сумма распространяется на все заявки,
пришедшие за время T
тогда,
1
1
Lсист
ti
ti
T i
T i

61. Формула Литтла

величина T - среднее число заявок,
пришедших за время Т
среднее время пребывания заявки в системе
сумма всех времен ti
среднее число пребывания заявки в системе
Wсист
t
i
T
i
1
* Lсист

62. II формула Литтла

среднее время пребывания заявки в очереди
среднее число заявок в очереди
интенсивно сть потока заявок
Wоч
1
Lоч

63. Одноканальная СМО с неограниченной очередью

;
Задача
на СМО с очередью поступает простейший
поток заявок с интенсивностью
простейший поток обслуживаний с
интенсивностью
1
tоб
Найти финальные вероятности состояний и
характеристики ее эффективности

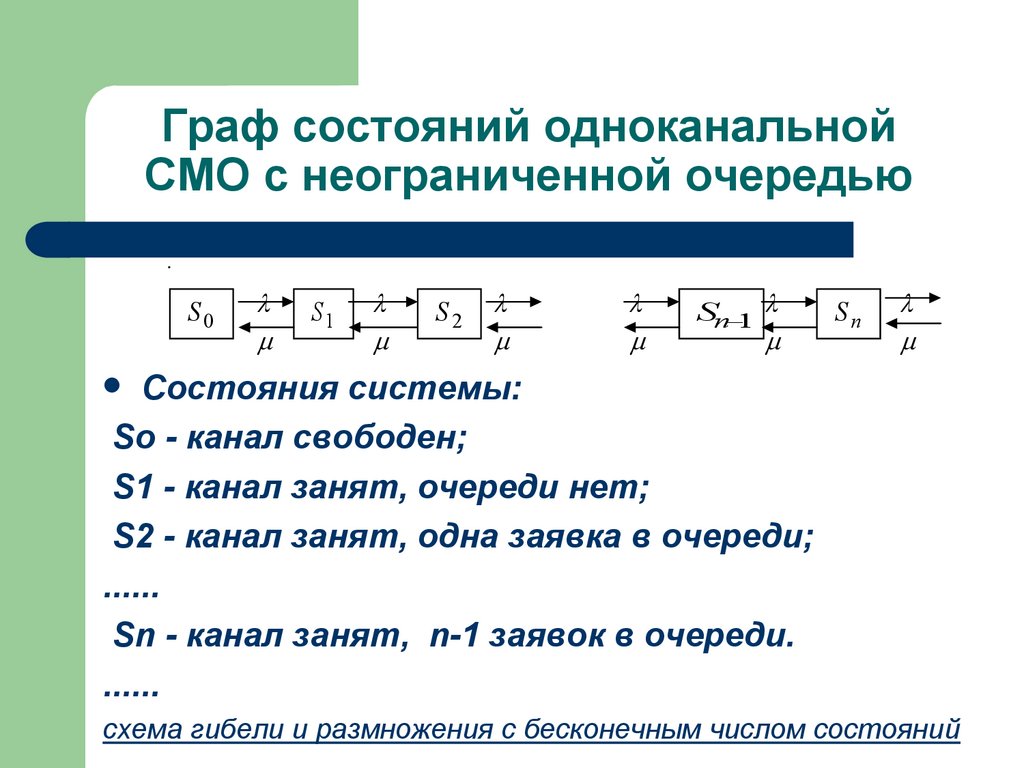
64. Граф состояний одноканальной СМО с неограниченной очередью

.
S0
S1
S2
Sn 1
Sn
Состояния системы:
So - канал свободен;
S1 - канал занят, очереди нет;
S2 - канал занят, одна заявка в очереди;
......
Sn - канал занят, n-1 заявок в очереди.
......
cхема гибели и размножения с бесконечным числом состояний

65. Финальные вероятности

существуют только тогда, когда система
не перегружена ( 1 ). Если приведенная
интенсивность потока заявок больше либо
равна единице ( 1), при t очередь
неограниченно растет.
p0 1
2
2
3
3
n
n
1
1
1

66. Финальные вероятности

Ряд в формуле представляет собой
геометрическую прогрессию и при 1
сходится
1
1
p0
1
1
p1 p0
p 2 2 p0
p n n p0
самое вероятное состояние – канал свободен

67. Показатели эффективности

абсолютная пропускная способность
A=
относительная пропускная
способность
Q=1
среднее число заявок в системе
Lсист
1

68. Показатели эффективности

среднее время пребывания заявки в
системе (по формуле Литтла)
Wсист
1
Lсист
(1 )
вероятность того, что канал занят
Pзан 1 p0

69. Показатели эффективности

среднее число заявок в очереди
разность среднего числа заявок в системе и
их среднего числа под обслуживанием
Lоч Lсист Lоб
число заявок под обслуживанием
Lоб 0 p0 1 Pзан
канал свободен канал занят

70. Показатели эффективности

среднее число заявок в очереди
2
Lоч Lсист Lоб
1
1
среднее время пребывания заявки в очереди
Wоч
1
Lоч
2
(1 )

71. Многоканальная СМО с неограниченной очередью

;
Задача
на СМО с очередью поступает простейший
поток заявок с интенсивностью
простейший поток обслуживаний с
интенсивностью
1
tоб
Найти финальные вероятности состояний и
характеристики ее эффективности

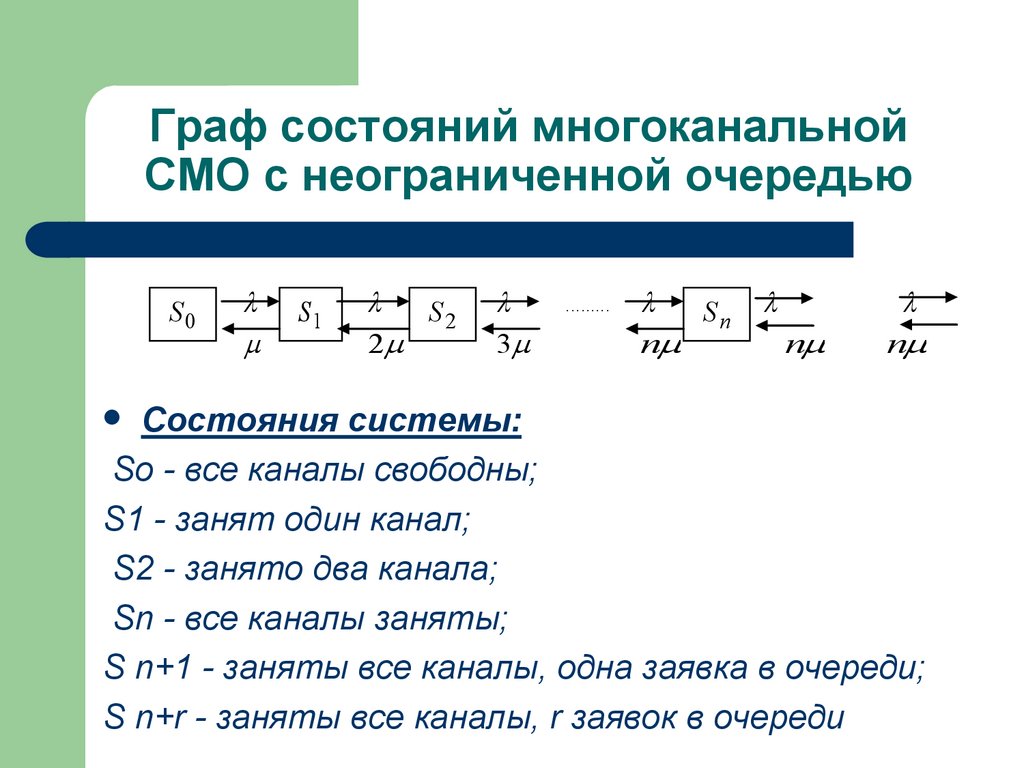
72. Граф состояний многоканальной СМО с неограниченной очередью

S0
S1
S2
2
3
.........
Sn
n
n
n
Состояния системы:
So - все каналы свободны;
S1 - занят один канал;
S2 - занято два канала;
Sn - все каналы заняты;
S n+1 - заняты все каналы, одна заявка в очереди;
S n+r - заняты все каналы, r заявок в очереди

73. Финальные вероятности

существуют, если
1
n
если
1 очередь неограниченно растет
n
n 1
p0 1
2
!
3
!
n
!
n
!
(
n
)
2
p1 p0
pn 1
n 1
n n!
3
p2
p0
n
2
2!
p0
pn
n r
1
n
n!
pn r r
p0
n n!
p0

74. Характеристики эффективности

среднее число занятых каналов
среднее число заявок в очереди
n 1 p0
r 1
Lоч r pn r
n n! 1
n
k
2
среднее число заявок в системе
Lсист Lоч k Lоч

75. СМО с ограниченной очередью

Число заявок в очереди ограниченно, т.е. не
может превосходить некоторого числа m
Если в очередь поступает m+1 заявка, она
покидает систему необслуженной
(получает отказ)

76. СМО с ограниченным временем ожидания

Городские транспортные системы
пассажиры ожидают транспортного
обслуживания данным транспортным
средством ограниченное время, а далее
могут предпочесть другой вид транспорта
Технологические системы
длительное ожидание обработки сырья
приводит к потере качества продукции
Системы оперативного управления
важна срочность передачи информации

77. СМО с ограниченным временем ожидания

Заявка может находиться в очереди случайное время,
распределенное по показательному закону с
некоторым параметром
т.е. каждая заявка, стоящая в очереди на
обслуживание, может покинуть систему с
интенсивностью

78. Основное допущение при анализе рассмотренных СМО

все потоки событий, переводящие
системы массового обслуживания из
состояния в состояние - простейшие
При нарушении этого требования имеются лишь
отдельные результаты, позволяющие выразить в
аналитическом виде характеристики СМО через
параметры задачи

79.

Спасибо за внимание!