Модель Эрланга с ожиданием и блокировками (вторая модель Эрланга). Заявка освобождает место в очереди

1. Модель Эрланга с ожиданием и блокировками (вторая модель Эрланга). Заявка освобождает место в очереди

Курс «Математическая теория телетрафика»
Модель Эрланга с
ожиданием и блокировками
(вторая модель Эрланга).
Заявка освобождает место в очереди
Лекция 7а

2.

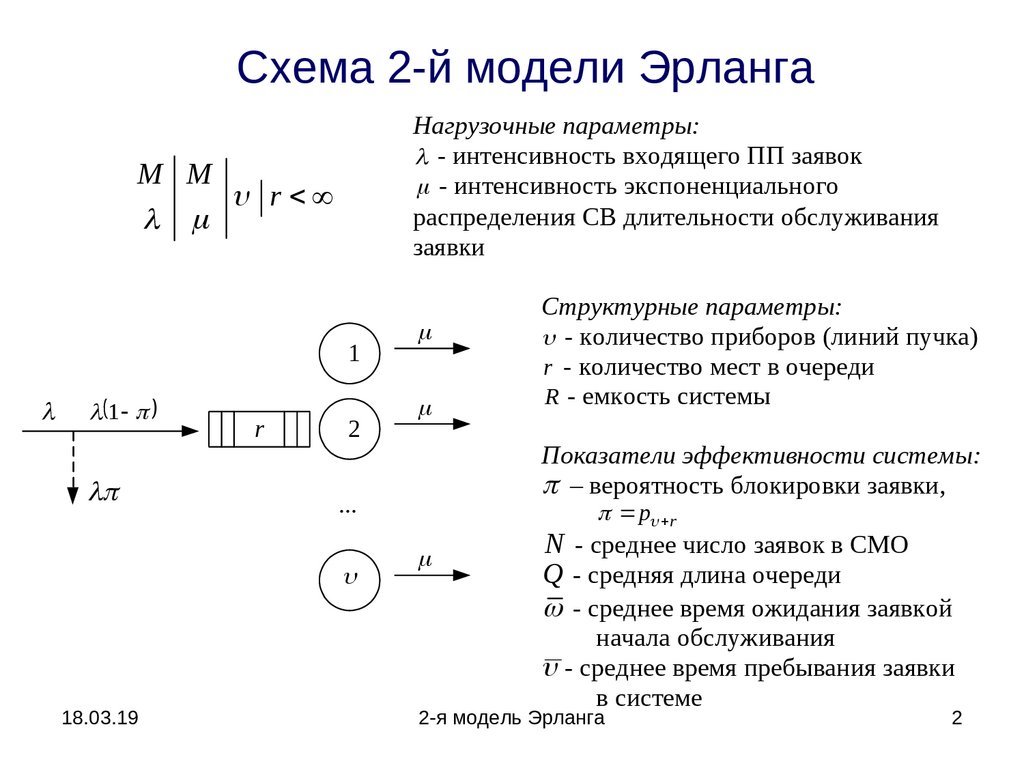
Схема 2-й модели Эрланга
Нагрузочные параметры:
- интенсивность входящего ПП заявок
- интенсивность экспоненциального
распределения СВ длительности обслуживания
заявки
M M
r
1
1
r
2
Показатели эффективности системы:
– вероятность блокировки заявки,
...
18.03.19
Структурные параметры:
- количество приборов (линий пучка)
r - количество мест в очереди
R - емкость системы
p r
N - cреднее число заявок в СМО
Q - cредняя длина очереди
- cреднее время ожидания заявкой
начала обслуживания
- cреднее время пребывания заявки
в системе
2-я модель Эрланга
2

3.

Физическая модель
• обслуживание хэндоверов в соте ССПС
• центральный процессор узла коммутации
• канал передачи данных
18.03.19
2-я модель Эрланга
3

4.

Математическая модель
X (t ) - число заявок в СМО в момент t , t 0
J 0,1, , R - пространство состояний системы,
Случайный процесс (СП) X (t ) – ПРГ, X (t ) J
pn lim P{ X (t ) n} - стационарная вероятность
t
состояния n J
n J - стационарное распределение вероятностей
ПРГ X (t )
pn ,
18.03.19
2-я модель Эрланга
4

5.

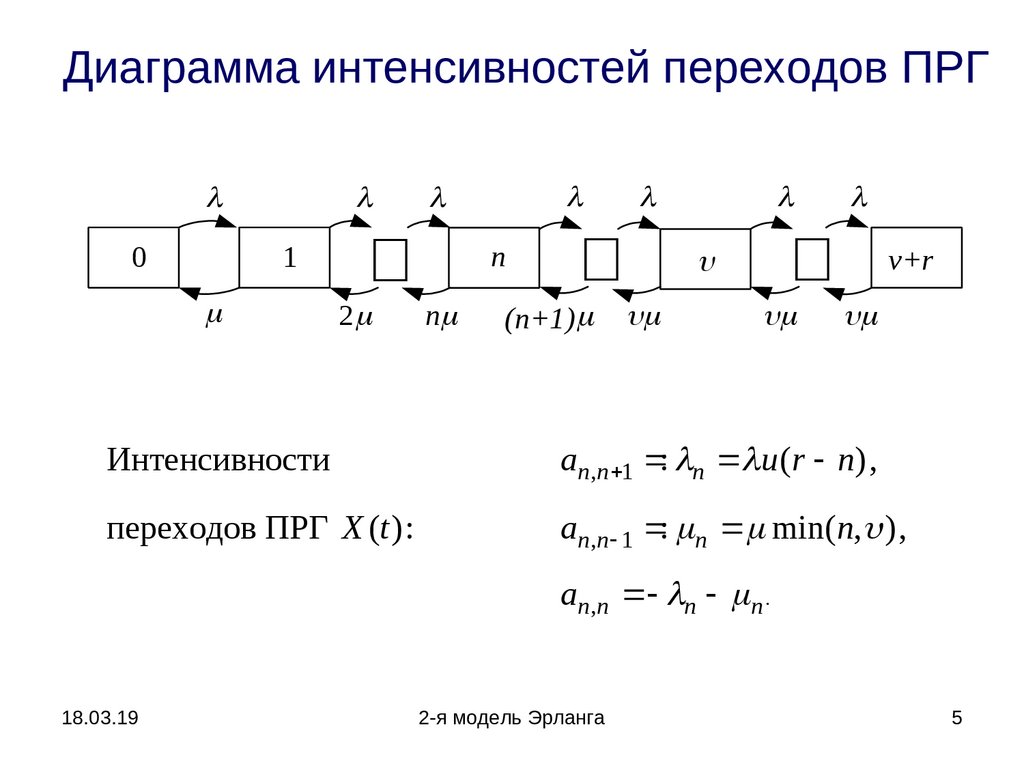
Диаграмма интенсивностей переходов ПРГ
0
1
2
n
n
(n+1)
v+r
Интенсивности
an,n 1 : n u (r n) ,
переходов ПРГ X (t ) :
an,n 1 : n min(n, ) ,
an,n n n .
18.03.19
2-я модель Эрланга
5

6.

СУГБ
p0 p1 0 ;
pn 1 ( n ) pn (n 1) pn 1 0 , n 1, 1;
pn 1 ( ) pn v pn 1 0 , n , r 1;
p r 1 p r 0 .
18.03.19
2-я модель Эрланга
6

7.

СУЛБ
pn 1 n pn , n 1, ;
pn 1 pn , n , r .
Условие нормировки:
r
pn 1
n 0
18.03.19
2-я модель Эрланга
7

8.

Стационарное распределение (1/3)
n
p0 , n 0, ;
n!
pn
n
n
p
p , n , r.
n 0
!
Здесь
- предложенная нагрузка на СМО
18.03.19
2-я модель Эрланга
8

9.

Стационарное распределение (2/3)
r
p0 определяется из условия нормировки
pn 1:
n 0
p0
1
n
r
n! !
n 0
n
n 1
1 n
1
n 0 n! !
1
18.03.19
1
n
r
m 1
n 0 n! ! m 0
r 1 1
.
2-я модель Эрланга
9

10.

Стационарное распределение (3/3)
r 1 1
n
1
1 n
, n 0, 1;
n ! n! !
n
0
1
pn
1
r
1
1 n
n
1
, n , r.
n
!
n 0 n! !
1
При r условие существования стационарного режима
.
18.03.19
2-я модель Эрланга
10

11.

Стационарный режим
Условия Карлина и МакГрегора
существования стационарного режима при C :
i
j
i 1
j 1
j
i
j 1
i 1
18.03.19
j 1
(7.3)
(7.4)
j
2-я модель Эрланга
11

12. Упражнения

Упражнение 7.1. Для СМО
M M
r выписать
- пространство состояний;
- матрицу Α ,
- диаграмму интенсивностей переходов;
- СУГБ и СУЛБ;
- стационарное РВ;
- условия существования стационарного режима
при r .
Упражнение 7.2. Для СМО
M M
1
получить
формулы для величин среднего числа N заявок в СМО
и средней длины Q очереди.
18.03.19
2-я модель Эрланга
12

13.

Вероятностные характеристики
Вероятность блокировки заявки:
p r , r
Среднее число N заявок в СМО:
r
N npn
n 0
Средняя длина Q очереди (ср. число заявок в очереди):
r
Q 0 p0 p1 ... p 1 p 1 2 p 2 ... r p r np n
n 1
26.11.2010
2-я модель Эрланга
13

14.

Вероятностно-временные характеристики
– случайная величина (СВ) времени обслуживания,
B t P t exp - ФР СВ ,
1
M tdB t - ср. значение СВ .
0
– СВ времени ожидания начала обслуживания,
W t P t - ФР СВ ,
M - ср. значение СВ .
– СВ времени пребывания заявки в СМО,
V t P t ,
M - ср. значение СВ .
26.11.2010
2-я модель Эрланга
14

15.

Время ожидания начала обслуживания
– СВ времени ожидания начала обслуживания,
W t P t - ФР СВ ,
M - ср. значение СВ .
Вероятность немедленного обслуживания:
r 1
1 n
1
1
P 0 pn
n 0 n! !
n 0
1
26.11.2010
2-я модель Эрланга
1
n
n!
n 0
1
15

16.

Вторая формула Эрланга
Вероятность неявных потерь для СМО
P 0 pn p0
!
n
n
n
M M
:
!
1 n
n! !
n 0
Упражнение 7.3. Выразить P 0 через E ( , ) .
26.11.2010
2-я модель Эрланга
16

17.

ФР времени ожидания заявки
Пусть в момент t поступления заявки в СМО X t i , i 0, r .
i r :
P заявка будет потеряна p r
i 0, r 1: P заявка будет принята в СМО 1 1 p r
i 0, 1:
P заявка немедленно начнет обслуживат ься
1
P 0 pn
n 0
i , r 1: заявка ожидает начала обслуживания в течение
времени, необходимого для обслуживания полностью
загруженной системой i 1 заявок.
P i 1 заявок покинет СМО за время t Ei 1 t
- ФР Эрланга с параметрами и i 1 .
26.11.2010
2-я модель Эрланга
17

18.

ПЛС ФР времени ожидания заявки
1
ФР W t P t
1
r 1
1
pn pi Ei 1 t
i
n 0
r 1
1
P 0 p j E j 1 t
1
j 0
ПЛС s , s 0 , СВ :
r 1 j
1
st
st
P 0 p j e dE j 1 t
s e dW t
1
j 0 0
0
r 1
1
j
j 1
P 0 p
j
j
1
1
j 0 s
26.11.2010
2-я модель Эрланга
18

19.

Среднее время ожидания заявки
ПЛС s , s 0 , ФР W t :
r 1
1
j
P 0 p
s
j
1
1
j 0 s
r
1
1
s
P 0 p
1
s
Среднее время ожидания :
r
r 1 r
p
0
1
2
26.11.2010
2-я модель Эрланга
19

20.

ФР времени пребывания заявки в СМО
= +
ФР V t P t - ?
ПЛС s , s 0 , ФР V t :
r
1
1
s
P 0 p
s e st dV t
1
s s
0
Среднее время пребывания :
1
0
26.11.2010
2-я модель Эрланга
20

21.

Интенсивность принятой нагрузки
Суммируем уравнения ЛБ:
r
r
pn 1 (1 ) npn pn
n 1
n 1
n 1
Здесь - вероятность потерь (по времени);
(1 ) - интенсивность принятого потока (пропускная
способность системы);
r
npn
n 1
pn - среднее число занятых приборов;
n 1
r
npn pn - средняя интенсивность
n 1
n 1
обслуженного потока.
26.11.2010
2-я модель Эрланга
21