Л4_ 25 комплексные числа

1.

Дисциплина «МАТЕМАТИКА»
Тема 04. Введение в математический
анализ
Занятие 25. Комплексные числа

2.

Учебные вопросы
1. Определение множества комплексных
чисел. Геометрическое изображение
комплексных чисел.
2. Операции над комплексными числами в
алгебраической форме.
3. Модуль и аргумент комплексного числа,
его тригонометрическая форма.

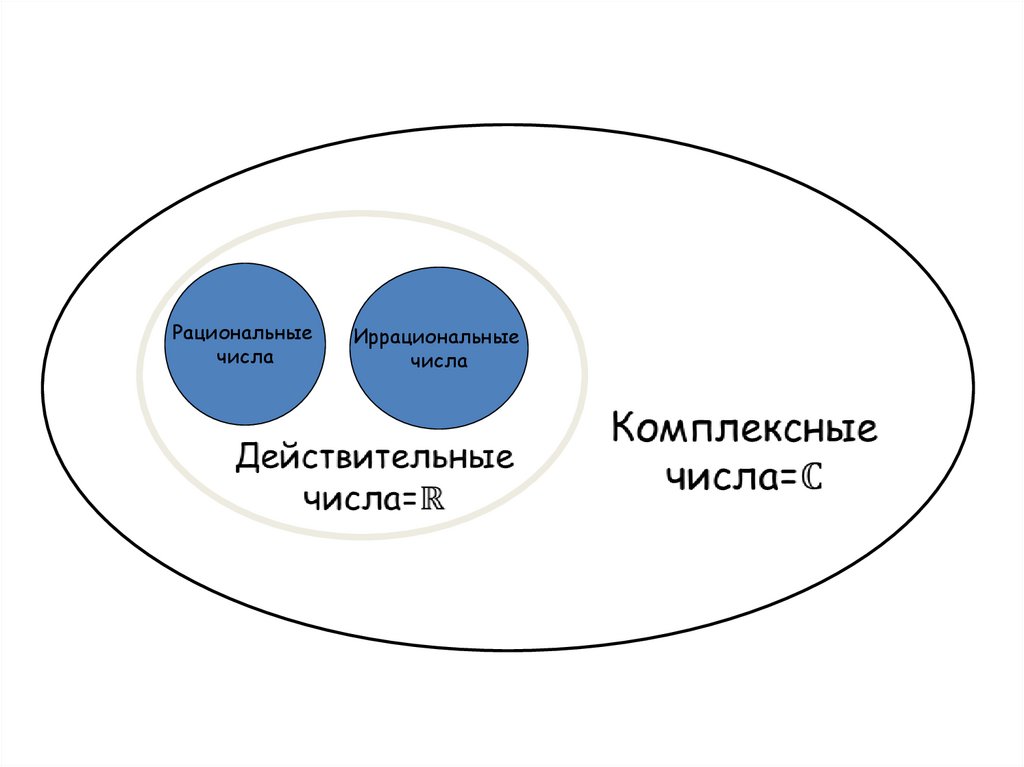
3. Понятие комплексного числа

Х+А=В - недостаточно положительных
Х+5=2
чисел
А·Х + В=0 (А≠0) – разрешимы на
множестве рац.чисел
Х²=2 или Х³=5 - корни - иррациональные
числа

4.

Рациональные
числа
Иррациональные
числа
Действительные числа

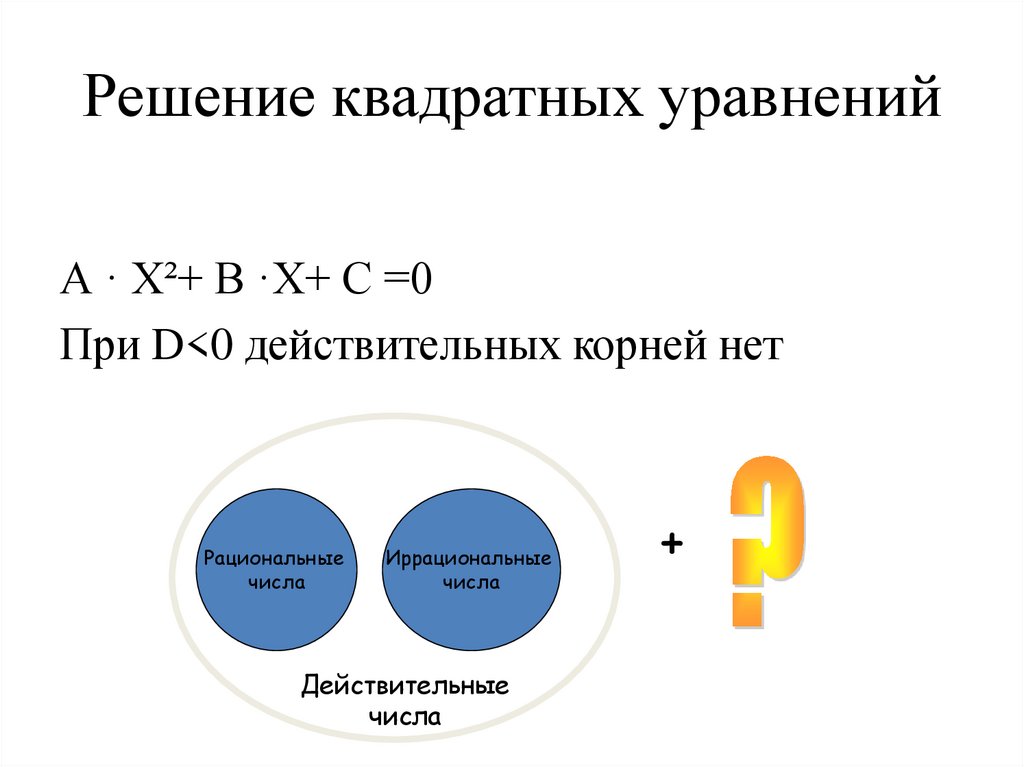
5. Решение квадратных уравнений

А · Х²+ В ·Х+ С =0
При D<0 действительных корней нет
Рациональные
числа
Иррациональные
числа
Действительные
числа
+

6.

Рациональные
числа
Иррациональные
числа

7.

8.

Учение о комплексных числах и теория
функций комплексного переменного нашли
важнейшее применение в теории
электричества, электротехнике,
основы радиотехники, в ядерной физике,
широко используются
в курсах
«Теоретические основы электро- и
радиоцепей»,
«Основы теории связи».

9.

1.
Определение множества комплексных чисел.
Геометрическое изображение комплексных
чисел.
Определение 1.
Символ вида a + b j
комплексным числом.
называется

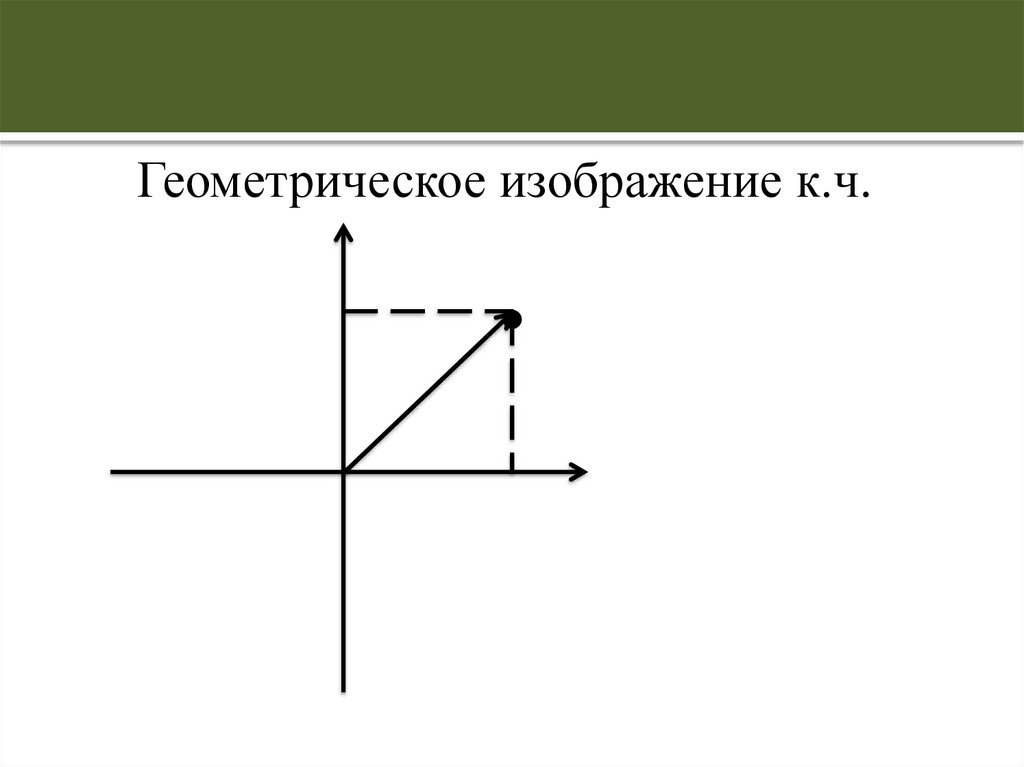
10.

Комплексные числа принято изображать точками
на плоскости (х0у). А именно, комплексному
числу z = a + b j ставится в соответствие точка
Р(a; b).

11.

Геометрическое изображение к.ч.

12.

2. Операции
наднад
комплексными
числами в
1.
Операции
комплексными
числами в алгебраической форме.
алгебраической форме
z1 = a1 b1 j
и
z2 a2 b2 j
1. z 3 = ( a1 a2 ) + ( b1 b2 ) j .
2. z 4 = ( a1 a2 ) + ( b1 b2 ) j
3. z 1 z 2 = ( a 1 a 2 – b 1 b 2 ) + ( a 1 b 2 + a 2 b 1 ) j
z1 z2 ( a1 b1 j ) ( a2 b2 j )
2
2
2
4. z2
=
=
a2 b2
a1 a2 b1 b2
a2 b1 a1 b2
= a22 b22 + j a22 b22

13.

Результаты текущей успеваемости 1 года обучения
3. Модуль и аргумент
комплексного
числа, его
за сентябрь
месяц
тригонометрическая форма.
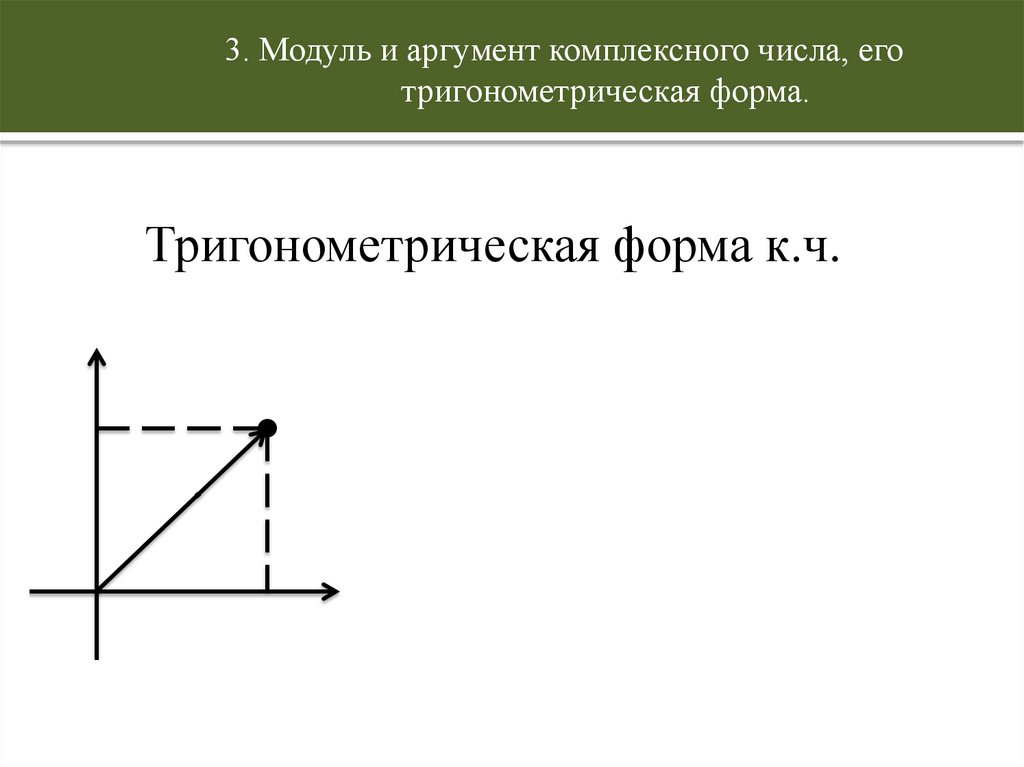
Из рис.1 следует = z =
а 2 b2 -модуль
комплексного числа z = a + b j,
а = сos , b = sin .
Комплексное число z = a + b j = сos + j sin =
(сos + j sin ) .
Запись
z = (сos + j sin )
называется
тригонометрической формой комплексного числа.

14.

3. Модуль и аргумент комплексного числа, его
тригонометрическая форма.
Тригонометрическая форма к.ч.

15.

Комплексные числа
z(x;y)
Алгебраическая
форма
Тригонометрическая
форма
Показательная
форма

16.

Форма записи
комплексного числа
Алгебраическая
форма
z x j y
x- вещественная часть к.ч
y- мнимая часть к.ч.
Тригонометрическая
форма
z r (cos j sin )
r модуль к.ч.
- аргумент к.ч.
Показательная
форма
z r e j
r модуль к.ч.
- аргумент к.ч.
Операции над комплексными числами в данной форме
z1 z 2 ( x1 x2 ) j ( y1 y2 )
z1 z 2 ( x1 x2 ) j ( y1 y2 )
z1 z 2 ( x1 x2 y1 y2 ) j ( x1 y2 x2 y1 )
z1 z1 z 2
z2 z2 z2
z n ( x j y) n
z1 z 2 r1 r2 (cos( 1 2 ) j sin( 1 2 )
z1 r1
(cos( 1 2 ) j sin( 1 2 ))
z 2 r2
z n rn (cos n j sin n )
2 k
2 k
n
n
z r (cos
n
j sin
z1 z 2 r1 r2 e j ( 1 2 )
z1 r1 j ( 1 2 )
e
z 2 r2
z n r n e jn
n
z r e
n
j
2 k
n
, k 0,1,...n 1
n
), k 0,1,...n 1

17.

x
r x 2 y 2 ; ( знак y ) arccos( );
r
x r cos ; y r sin
Формулы перехода из а.ф. в т.ф.:
Формулы перехода из т.ф. в а.ф.:
Значения тригонометрических функций для некоторых аргументов:
Ф-ия
0( 0 )
6
(30 )
4
(45 )
sin
0
cos
1
2
2
2
1
3
2
2
2
3
(60 )
3
2
1
2
2
(
180
)
(90 )
3
(270 )
2
2 (360 )
1
0
-1
0
0
-1
0
1