Комплексные числа

1. Комплексные числа

• Историческая справка
• Основные понятия
• Геометрическое изображение
комплексных чисел
• Тригонометрическая форма записи
комплексных чисел
• Сопряженные числа
• Операции над комплексными числами
• Показательная форма записи
комплексного числа
• Множества комплексных чисел

2. Историческая справка

3.

Историческая справка

4. Историческая справка

5. Основные понятия

Комплексным числом z называют выражение:
z a i b,
где а и b – действительные числа,
i – мнимая единица, определяемая равенством:
i 1, i 2 1
а называется действительной частью числа z,
b – мнимой частью. Их обозначают так:
a Re z; b Im z.

6. Геометрическое изображение комплексных чисел

(z)
r

7. Геометрическое изображение комплексных чисел

arg z - разрез по Re z 0
0 arg z 2
- разрез по Re z 0

8. Тригонометрическая форма записи комплексных чисел

9. Сопряженные числа

(z)

10. Сопряженные числа

z z a b z
2
2
2

11. Операции над комплексными числами

1
Равенство комплексных чисел
Два комплексных числа z1 a1 i b1 и z2 a2 i b2
называются равными : z1 z 2 , если a1 a2 , b1 b2
Комплексное число z a i b равно нулю, тогда и только
тогда, когда a 0, b 0
2
Сложение и вычитание комплексных чисел
Суммой (разностью) комплексных чисел z1 a1 i b1
и
z2 a2 i b2 называется комплексное число, определяемое
равенством:
z1 z2 a1 i b1 a2 i b2 a1 a2 i b1 b2
z1 z2 a1 i b1 a2 i b2 a1 a2 i b1 b2

12. Операции над комплексными числами

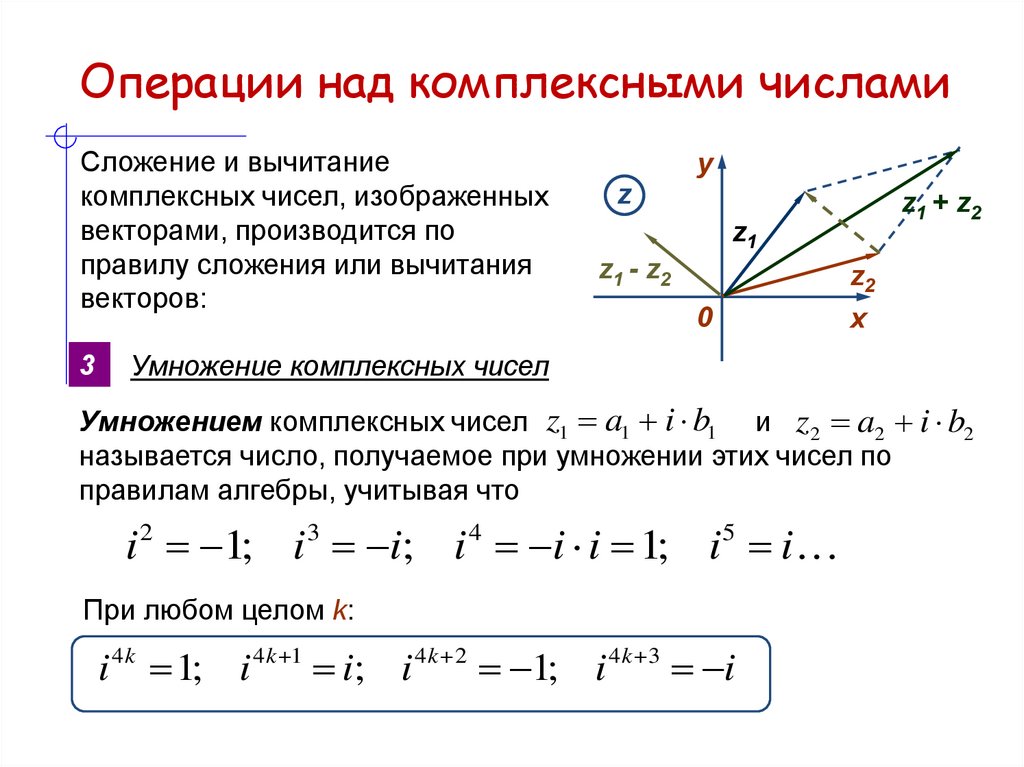
Сложение и вычитание
комплексных чисел, изображенных
векторами, производится по
правилу сложения или вычитания
векторов:
3
y
z
z1 + z2
z1
z1 - z2
z2
х
0
Умножение комплексных чисел
Умножением комплексных чисел z1 a1 i b1 и z2 a2 i b2
называется число, получаемое при умножении этих чисел по
правилам алгебры, учитывая что
i 1; i i; i i i 1; i i
2
3
4
5
При любом целом k:
i 4 k 1; i 4 k 1 i; i 4 k 2 1; i 4 k 3 i

13. Операции над комплексными числами

На основании этого правила получим:
z1 z2 a1 i b1 a2 i b2
a1 a2 i b1 a2 i b2 a1 i 2 b1 b2
z1 z2 a1 a2 b1 b2 i b1 a2 b2 a1
z1 z2 r1 r2 (cos( 1 2 ) i sin( 1 2 ))

14. Операции над комплексными числами

15. Операции над комплексными числами

4
Деление комплексных чисел
Чтобы разделить z1 a1 i b1 на z2 a2 i b2
необходимо умножить делимое и делитель на число, сопряженное
делителю:
z1 a1 i b1
(a1 i b1 ) (a2 i b2 )
z2 a2 i b2 (a2 i b2 ) (a2 i b2 )
(a1a2 b1b2 ) i (a2b1 a1b2 ) a1a2 b1b2
a2b1 a1b2
2
i 2
2
2
2
a2 b2
a2 b2
a2 b22
z1 r1
(cos( 1 2 ) i sin( 1 2 ))
z2 r2

16. Операции над комплексными числами

17. Операции над комплексными числами

18. Операции над комплексными числами

19. Операции над комплексными числами

Найти произведение и частное комплексных чисел:
z1 2 3i,
z2 1 4i
z1 z2 2 3i 1 4i 2 3i 8i 12i 2
= -1
2 3i 8i 12 14 5i
z1 2 3i (2 3i) (1 4i) 2 3i 8i 12i 2
2
2
(1 4i ) (1 4i )
z2 1 4i
1 4
10 11
2 3i 8i 12 10 11i
i
17 17
17
17

20. Операции над комплексными числами

21. Операции над комплексными числами

5
Возведение в степень комплексного числа
z r (cos i sin )
При возведении комплексного числа
в
целую положительную степень модуль возводится в эту степень, а
аргумент умножается на показатель степени (формула Муавра)
z r (cos n i sin n )
n
n

22. Операции над комплексными числами

6
Извлечение корня из комплексного числа

23. Операции над комплексными числами

Для других значений k аргументы будут отличаться от полученных на
число, кратное 2π, и, следовательно будут получаться значения корня,
совпадающие с рассмотренными.
Итак, корень n – ой степени из комплексного числа имеет n различных
комплексных значений.
Корень n–ой степени из действительного числа также имеет n
значений, так как действительное число – частный случай комплексного
числа и может быть представлено в тригонометрической форме:
A A (cos0 i sin 0) ( A 0)
A A (cos i sin ) ( A 0)

24. Операции над комплексными числами

Найти все значения кубического корня из единицы
1 cos0 i sin 0 (r 1; 0)
0 2k
0 2k
2k
2k
1 cos
i sin
cos
i sin
3
3
3
3
k 0 3 1 cos 0 i sin 0 1
y
3
2
2
1
3
i
k 1 1 cos
i sin
2 2
3
3
4
4
1
3
3
k 2
1 cos
i sin
i
2 2
3
3
3
z
В
A
х
С

25. Операции над комплексными числами

26. Корни из единицы

Определение
Замечание

27. Корни из единицы

Замечание
Например (при n=4), правильный квадрат, вписанный в окружность
выглядит так:

28. Корни из единицы

Определение
Замечание

29. Корни из единицы

Теорема

30. Показательная форма записи комплексного числа

z r e
i
Действия над комплексными числами в показательной форме:
Пусть имеем: z1 r1 ei 1 ;
z1 z2 r1 r2 e
z2 r2 ei 2 . Тогда:
i 1 2
z1 r1 i 1 2
e
;
z2 r2
;
z n r n ei n ;
n
z n r e
i
2 k
n
.

31.

Показательная форма записи
комплексного числа

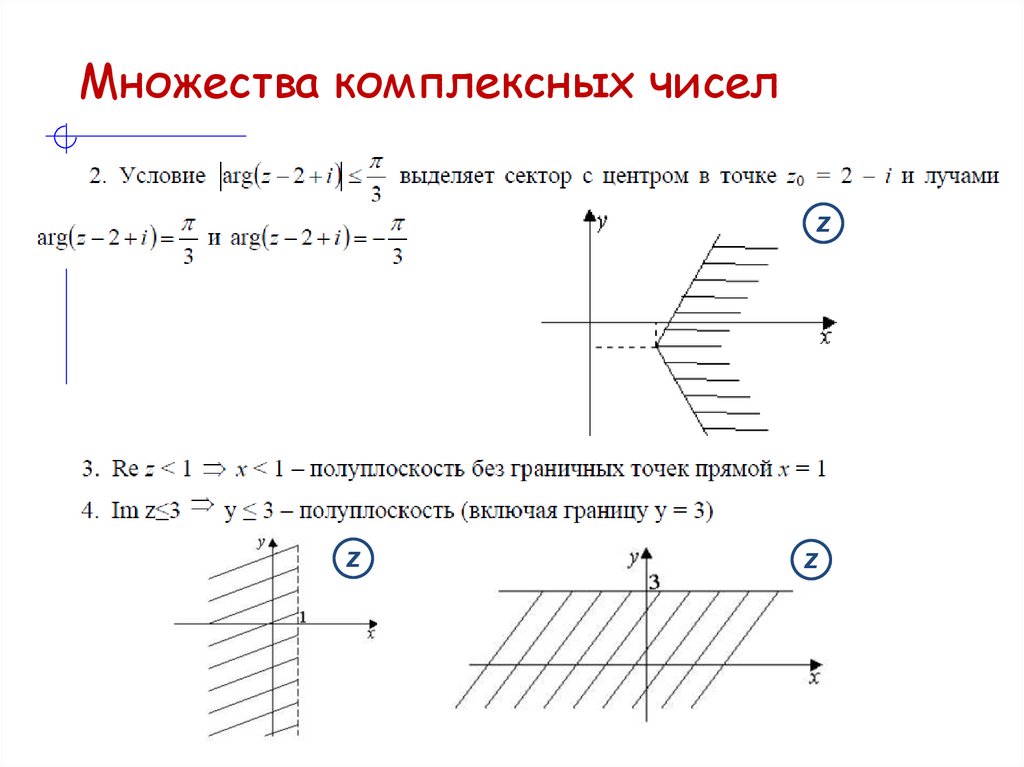
32. Множества комплексных чисел

z

33. Множества комплексных чисел

z
z
z