раздел 5 ПРЕЗЕНТАЦИЯ

1.

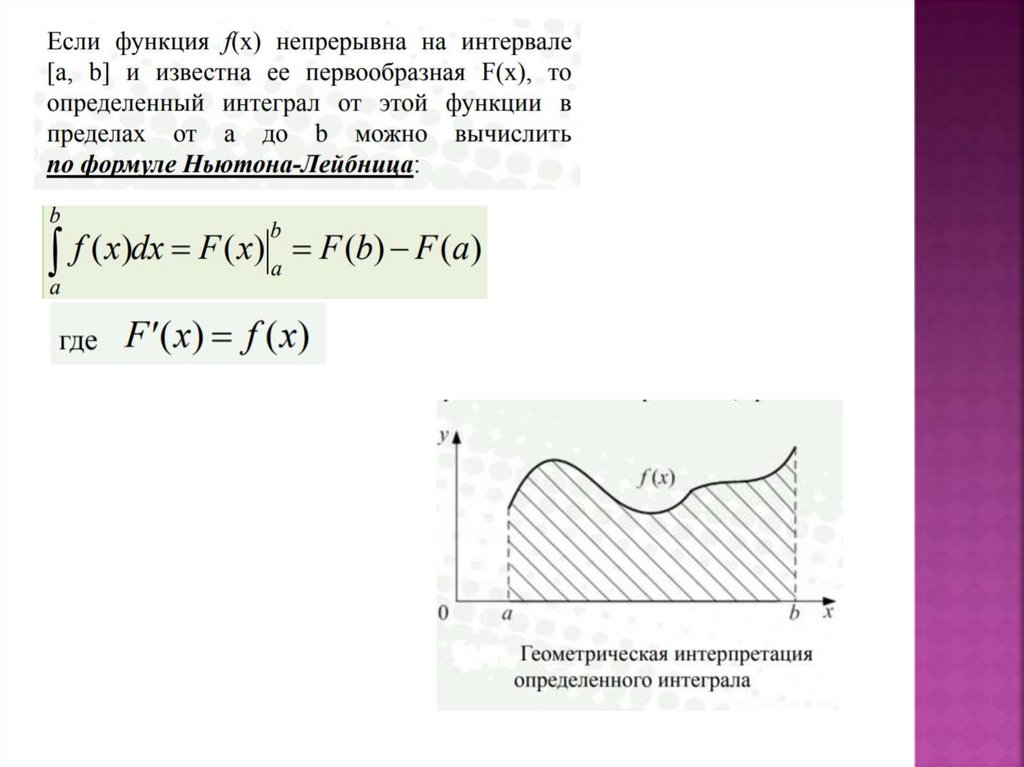
2. раздел 5. Численное дифференцирование и интегрирование функций

3. тема 1.

Численное
интегрирование

4.

5.

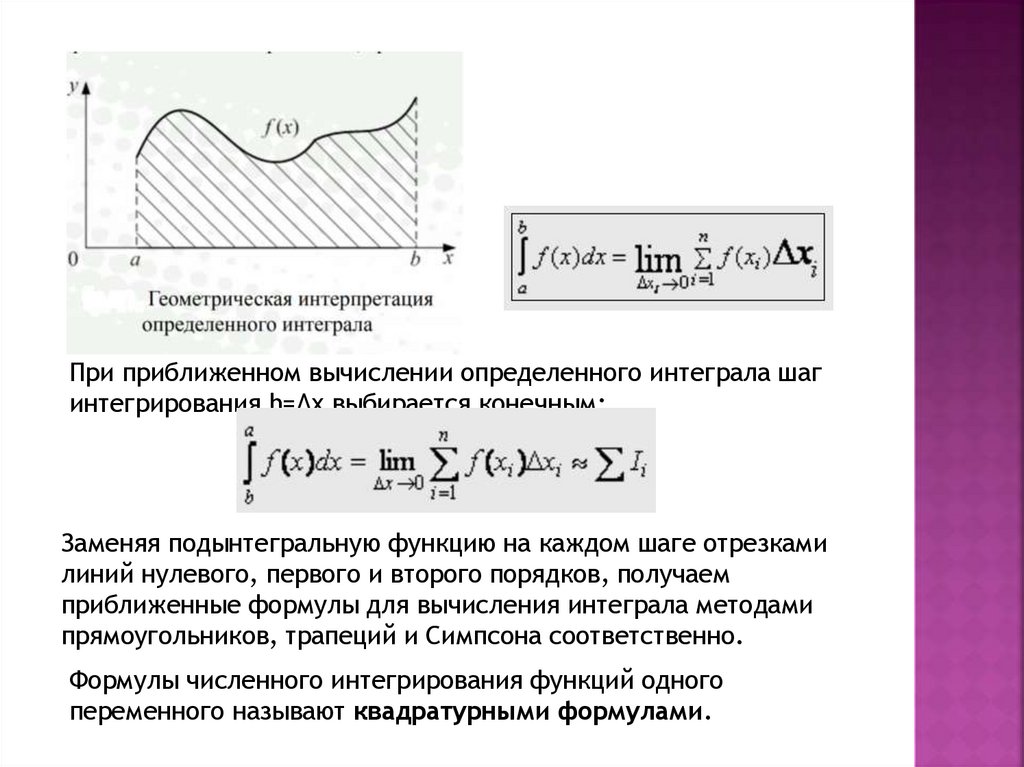
При приближенном вычислении определенного интеграла шаг
интегрирования h=∆x выбирается конечным:
Заменяя подынтегральную функцию на каждом шаге отрезками
линий нулевого, первого и второго порядков, получаем
приближенные формулы для вычисления интеграла методами
прямоугольников, трапеций и Симпсона соответственно.
Формулы численного интегрирования функций одного
переменного называют квадратурными формулами.

6. Постановка задачи

7. Формулы прямоугольников

Интерполяция полиномом нулевой степени.
Заменяем график функции F(x) горизонтальной линией (линий
нулевого порядка) и вычисляем значение элемента интегральной
суммы как площадь прямоугольника

8. Формула трапеций

Интерполяция полиномом первой степени.
Заменяем график функции F(x) прямой, проходящей через две точки
(х0,у0) и (х0+h,у1), и вычисляем значение элемента интегральной
суммы как площадь трапеции.

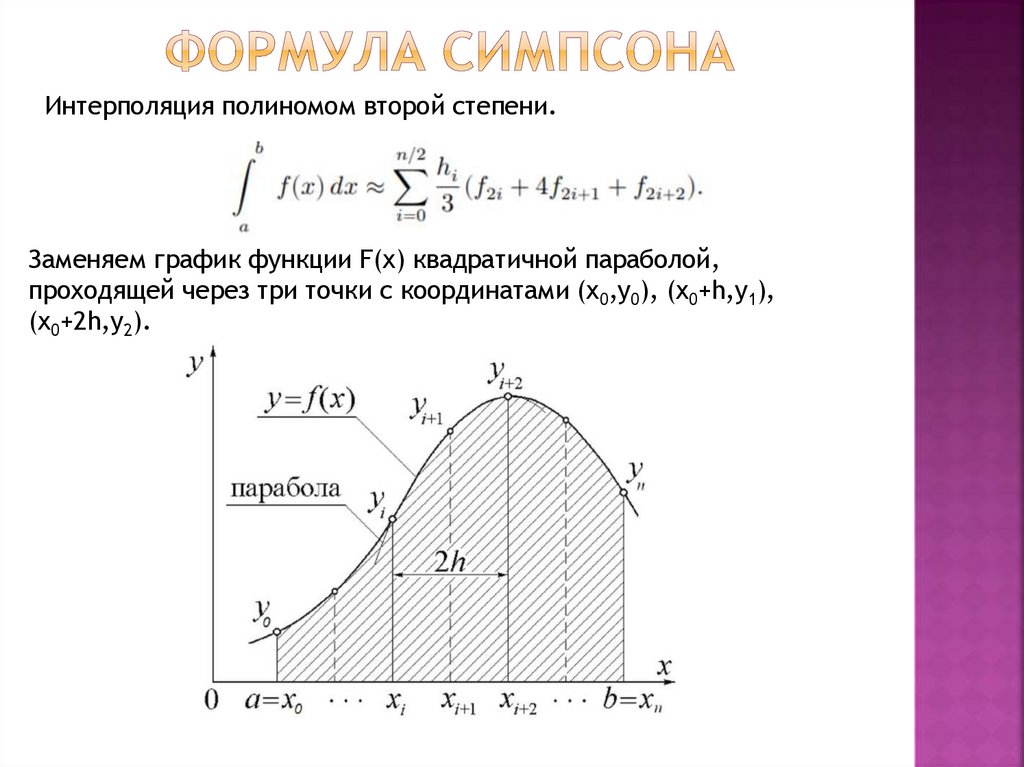
9. Формула симпсона

Интерполяция полиномом второй степени.
Заменяем график функции F(x) квадратичной параболой,
проходящей через три точки с координатами (х0,у0), (х0+h,у1),
(х0+2h,у2).

10. Формула симпсона

Вывод:

11. Формула симпсона

Вывод:

12. Формула симпсона

Вывод:

13. Формула симпсона

Эту же формулу для вычисления элемента интегральной суммы
получим, используя интерполяционный многочлен Лагранжа, в виде

14. Формула симпсона

15. Погрешности формул

16.

17.

18. тема 2.

Численное
дифференцирование

19.

Производная функции - это предел
отношения приращения функции к
приращению независимой переменной при
стремлении к нулю приращения
независимой переменной.
При численном нахождении производной заменим
отношение бесконечно малых приращений функций и
аргумента отношением конечных разностей. Очевидно,
что чем меньше будет приращение аргумента, тем точнее
численное значение производной.

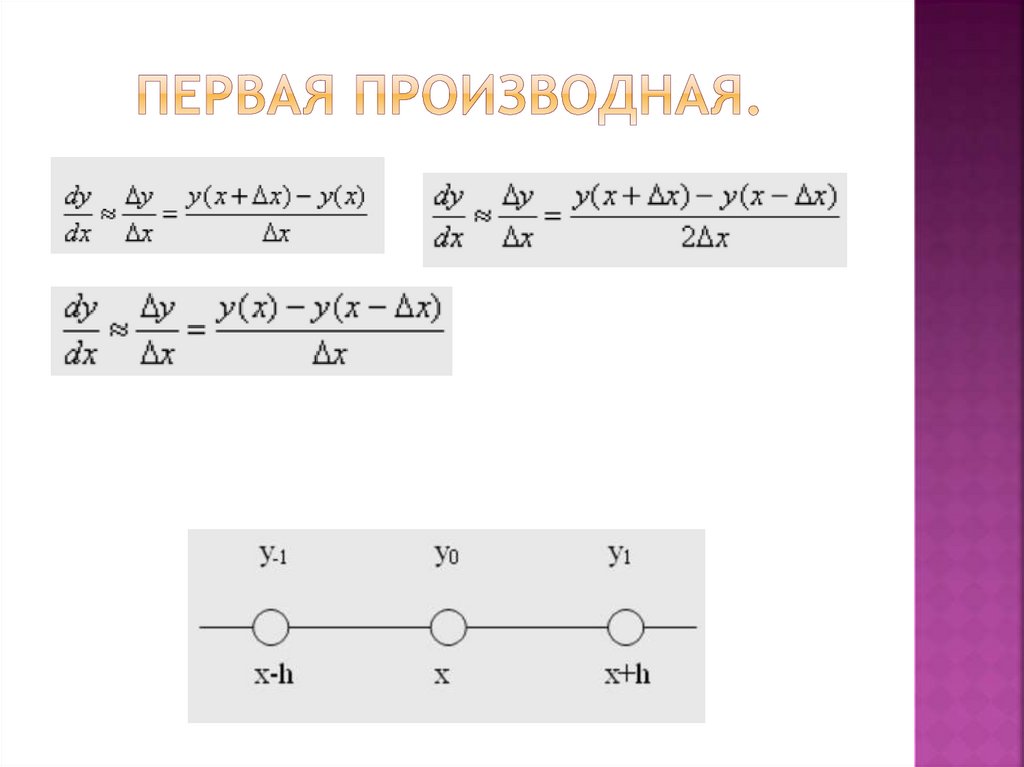
20. Первая производная. Двухточечные методы.

Для двухточечных методов при вычислении производных
используется значение функции в двух точках.
Приращение аргумента задается следующими способами:
1) откладывая Δx = h вправо от исследуемой точки
(правосторонняя/правая разность):
2) откладывая Δx = h влево от исследуемой точки
(левосторонняя/левая разность):

21. Первая производная. трехточечные методы.

Приращение аргумента задается следующим способом:
3) откладывая Δx = h в обе стороны от исследуемой точки
(двусторонняя/центральная разность):

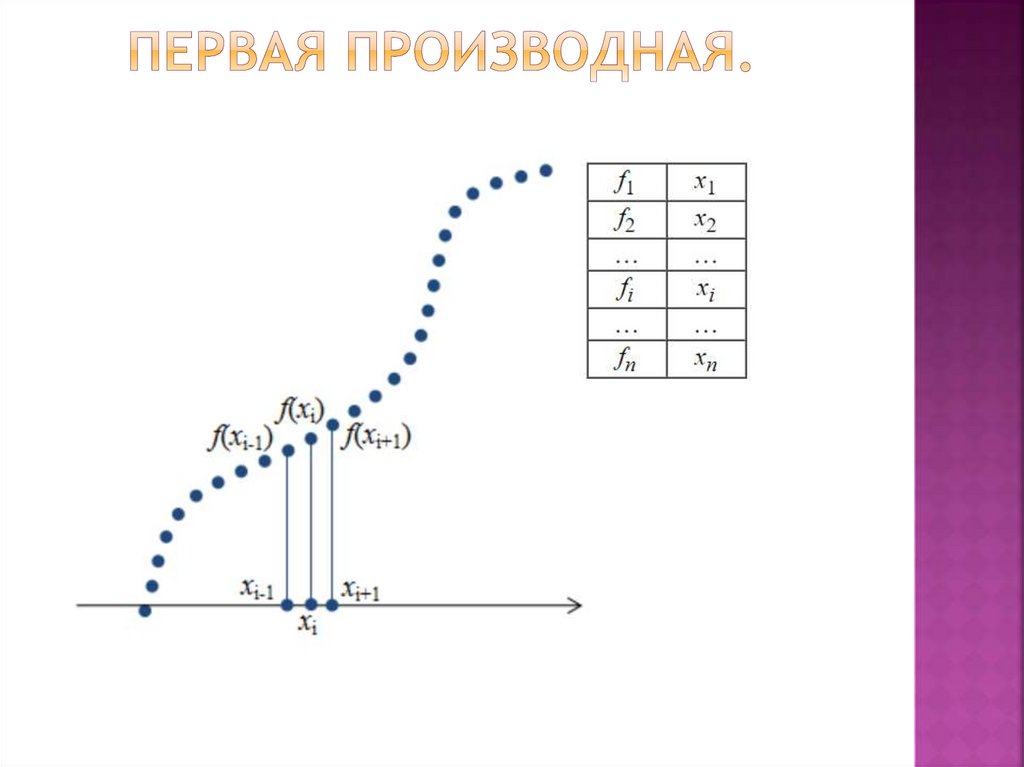
22. Первая производная.

23. Первая производная.

24. Первая производная.

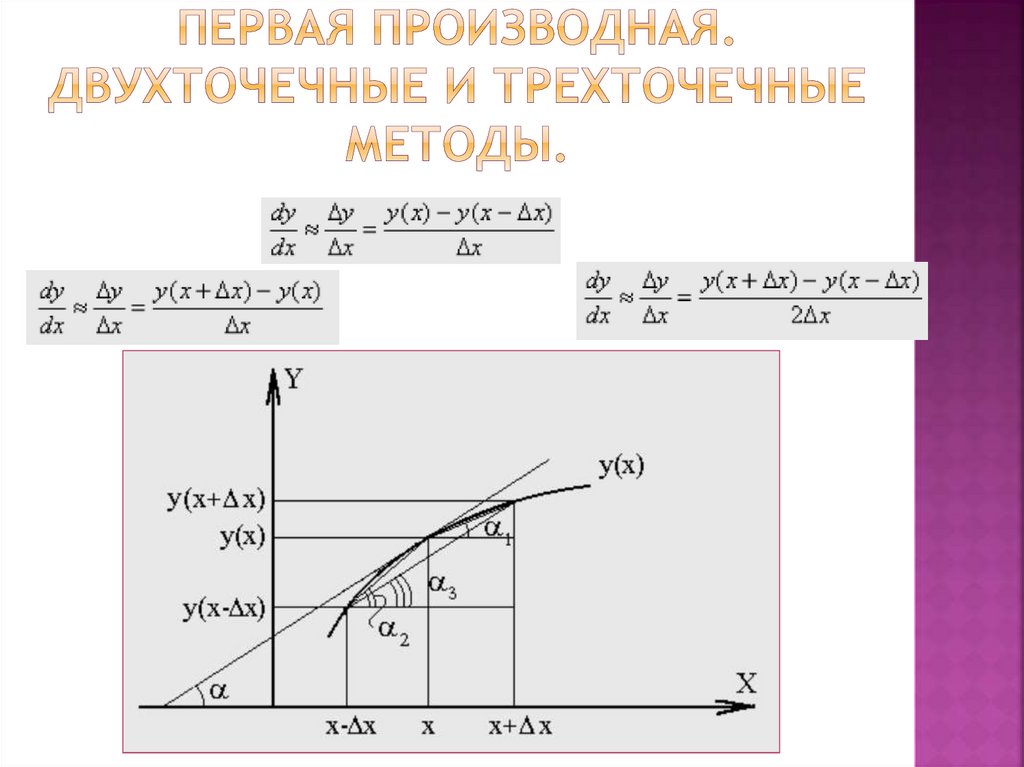
25. Первая производная. Двухточечные и трехточечные методы.

26. Первая производная. Двухточечные и трехточечные методы.

Пример.
Вычислить точное и приближенное (тремя методами)
значения производной функции y=x*x в точке x=1 с
шагом h=1 и h=0.001.
Решение.
Численное решение для шага: h=1

27. Первая производная. Двухточечные и трехточечные методы.

Пример.
Вычислить точное и приближенное (тремя методами)
значения производной функции y=x*x в точке x=1 с
шагом h=1 и h=0.001.
Решение.
Численное решение для шага: h=1
Для шага h=0.001

28. Первая производная. Двухточечные и трехточечные методы.

Пример.
Вычислить точное и приближенное (тремя методами)
значения производной функции y=x*x в точке x=1 с
шагом h=1 и h=0.001.
Решение.
Численное решение для шага: h=1
Для шага h=0.001
Аналитическое решение: y'=2x , y'(1)=2

29. Вывод формул

Будем считать, что в таблице используется равномерный
шаг.
Разложим f(xi−1) в ряд Тейлора в окрестности точки xi :

30. Вывод формул

Будем считать, что в таблице используется равномерный
шаг.
Разложим f(xi−1) в ряд Тейлора в окрестности точки xi :

31. Вывод формул

Будем считать, что в таблице используется равномерный
шаг.
Разложим f(xi−1) в ряд Тейлора в окрестности точки xi :

32. Вывод формул

Будем считать, что в таблице используется равномерный
шаг.
Разложим f(xi−1) в ряд Тейлора в окрестности точки xi :

33. Вывод формул

Будем считать, что в таблице используется равномерный
шаг.
Разложим f(xi−1) в ряд Тейлора в окрестности точки xi :

34. Вывод формул

35. Вывод формул

36. Вывод формул

37. Вывод формул

38.

39. вторая производная. Пятиточечный метод.

Вторая производная вычисляется как первая производная
от первой производной.
Для следующей пятиточечной схемы расчетная формула имеет вид:

40. вторая производная. Пятиточечный метод.

Пример.
Найти вторую производную функции y = 2 * x4
в точке x=1 с шагом h=0.01.

41. вторая производная. Пятиточечный метод.

Пример.
Найти вторую производную функции y = 2 * x4
в точке x=1 с шагом h=0.01.
Решение.

42. Вывод формул

43. Производные старших порядков

Производные третьего порядка вычисляются как первая
производная от производной второго порядка и т.д.
При вычислении производных высоких порядков
производная (n)-го порядка считается первой производной
от (n-1)-го порядка.

44. Метод рунге. Формула с пересчетом

45. Формула рунге (Формула с пересчетом)

Выражение для аппроксимации производной в общем случае можно
представить в виде:
Запишем это соотношение в той же точке x при другом шаге h1 = kh:
Приравнивая правые части равенств, находим выражение для
главного члена погрешности аппроксимации производной:
Подставляя найденное выражение в первое равенство, получаем
формулу Рунге

46. Частное дифференцирование функции многих переменных

В этом случае все аргументы функции становятся
константами кроме аргумента, по которому проводится
дифференцирование, а требуемый порядок
производной получается путем последовательного
вычисления производных, вплоть до требуемого
порядка: