Динамика_3

1. Лекция 3

Теорема о движении центра масс: введение в
динамику механической системы; свойства
внутренних сил; центр масс механической
системы; теорема о движении центра масс
механической системы; закон сохранения
движения центра масс.

2.

Введение в динамику механической системы
Механическая система - совокупность материальных точек
или тел, находящихся в механическом взаимодействии
Силы, действующие на систему:
1. Внешние силы (e) – действующие на точки и тела
системы со стороны точек или тел, не входящих в состав
данной системы.
2. Внутренние силы (i) – силы взаимодействия между
материальными точками или телами, входящими в данную
систему.
Одна и та же сила может являться как внешней, так и
внутренней. Все зависит от того, какая механическая система
рассматривается.
Например: в системе Солнце, Земля и Луна все силы
тяготения между ними являются внутренними. При
рассмотрении системы Земля и Луна силы тяготения,
приложенные со стороны Солнца – внешние.

3.

Свойства внутренних сил:
1. Главный вектор всех внутренних сил системы равен
нулю:
R i Fki 0.
2. Главный момент всех внутренних
сил системы относительно любого
центра равен нулю:
i
M Oi M kO
0.
Или в проекциях на координатные оси:
F Xki 0;
FYki 0;
FZki 0.
i
M kx
0;
i
M ky
0;
i
M kz
0.

4.

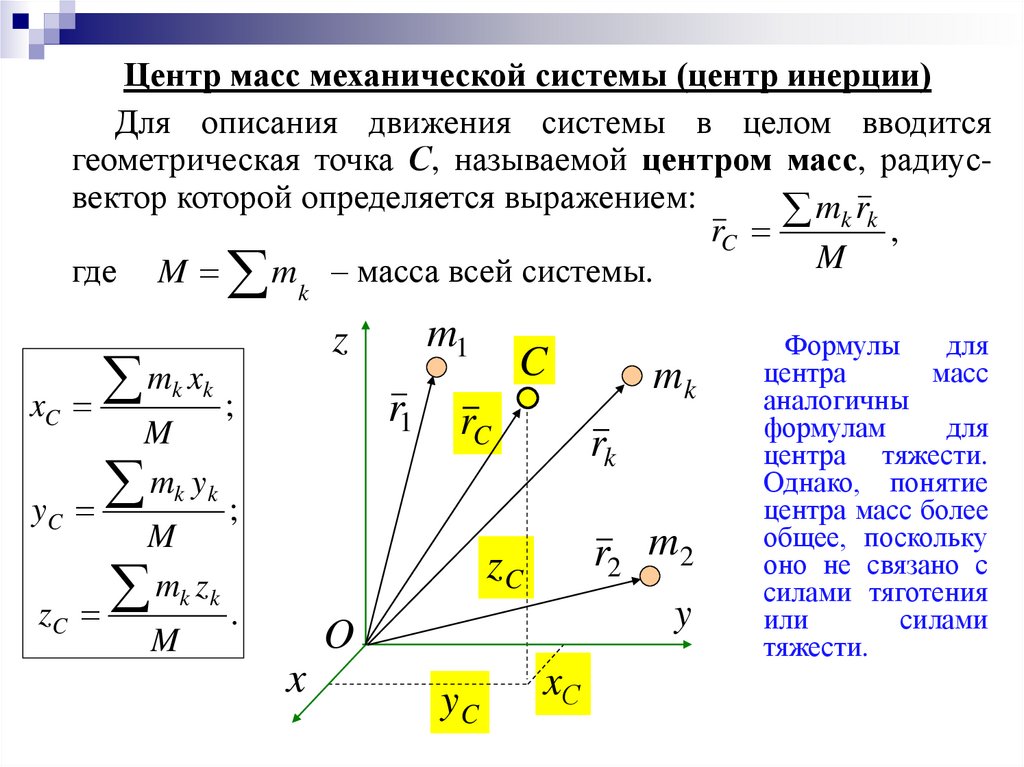
Центр масс механической системы (центр инерции)
Для описания движения системы в целом вводится
геометрическая точка С, называемой центром масс, радиусвектор которой определяется выражением:
mk rk
rC
,
M
где M
m – масса всей системы.
k
m x
x
;
k k
C
yC
zC
M
mk yk
M
mk z k
M
m1
z
r1
C
rC
rk
;
r2 m2
y
zC
.
O
x
yC
mk
xС
Формулы
для
центра
масс
аналогичны
формулам
для
центра тяжести.
Однако, понятие
центра масс более
общее, поскольку
оно не связано с
силами тяготения
или
силами
тяжести.

5.

Теорема о движении центра масс механической системы
Рассмотрим систему n материальных точек. Приложенные
к каждой точке силы разделим на внешние и внутренние и
заменим их на соответствующие равнодействующие Fke и Fki.
Запишем для каждой точки основное уравнение динамики:
2
d
rk
e
i
mk ak Fk Fk
mk 2 Fke Fki .
dt
2
d
rk
Просуммируем эти уравнения
mk 2
Fke Fki
по всем точкам:
dt
В левой части уравнения
R e Ri 0
внесем массы под знак d 2
e
производной и заменим
(
m
r
)
R
.
2 k k
сумму производных на dt
производную суммы:
Из определения центра масс:
MrC mk rk .
Подставим в полученное d 2
e
( MrC ) R .
2
уравнение:
dt

6.

После вынесения массы системы
за знак производной получаем:
M
d 2 rC
dt 2
Re
Произведение массы системы на ускорение ее центра
масс равно главному вектору внешних сил:
MaC R
e
M y R F ; - дифференциальные уравнения движения
центра масс в проекциях на оси координат
M z R F .
M x C R x
C
e
FXe k ;
e
e
Yk
y
e
C
z
e
Zk
Центр масс системы движется как материальная точка
массой, равной массе всей системы, к которой приложены все
внешние силы, действующие на систему.

7.

Закон сохранения движения центра масс
Следствия из теоремы о движении центра масс системы:
1. Если в интервале времени [t1, t2] главный вектор внешних
сил системы равен нулю, Re = 0, то скорость центра масс
постоянна, vC = const, аC = 0 (центр масс движется равномерно
прямолинейно).
2. Если в интервале времени [t1, t2] проекция главного
вектора внешних сил системы на ось X равна нулю, Rxe = 0 (Re
≠ 0), то скорость центра масс по оси X постоянна, vCx = const
(центр масс движется по оси равномерно).
Аналогичные утверждения справедливы для осей Y и Z.
3. Если в интервале времени [t1, t2] главный вектор внешних
сил системы равен нулю, Re = 0, и в начальный момент
скорость центра масс равна нулю, vC = 0, то радиус-вектор
центра масс остается постоянным, rC = const (центр масс
находится в покое – закон сохранения положения центра
масс).

8.

4. Если в интервале времени [t1, t2] проекция главного
вектора внешних сил системы на ось X равна нулю, Rxe = 0,
и в начальный момент скорость центра масс по этой оси
равна нулю, vCx = 0, то координата центра масс по оси X
остается постоянной, xC = const (центр масс не движется по
этой оси).
Аналогичные утверждения справедливы для осей y и z.